基于响应面法的电磁阀响应时间优化

蒋焕煜，张利君，周鸣川，施玮囡

（浙江大学生物系统工程与食品科学学院，杭州 310058）

基于响应面法的电磁阀响应时间优化

蒋焕煜，张利君，周鸣川，施玮囡

（浙江大学生物系统工程与食品科学学院，杭州 310058）

为了缩短喷雾植保用电磁阀的响应时间，提高变量喷雾的精准性，该文引入响应面法优化改进型脉冲宽度调制（pulse width modulation，PWM）控制参数。试验采用Box-Behnken设计方法，选取电磁阀驱动电压（10、12和14 V）、PWM延迟时间（15、40和65 ms）及PWM占空比（5%，15%和25%）作为考察因素，以电磁阀开启响应时间、电磁阀闭合响应时间和电磁阀响应时间为响应值，获取了关于3个响应值的二次多项回归模型，并对其进行了验证。经响应面法分析得出，在参数优化区间内，使电磁阀响应时间最短的参数条件为电磁阀驱动电压12 V、PWM延迟时间15 ms以及PWM占空比5%，与试验测量结果差异极小。与普通PWM控制方式相比，使用改进型PWM控制信号并优化控制参数可有效缩短电磁阀响应时间。该研究为合理选择PWM控制参数提供了参考。

阀；优化；模型；响应面法；喷雾植保；响应时间；电磁阀

0 引言

近年来，变量喷雾及对靶喷雾等环境友好型精准喷雾方式变得越来越重要[1-3]，脉冲宽度调制（pulse width modulation，PWM）变量喷施是目前精准喷雾过程中的重要控制方式。电磁阀作为PWM变量喷施系统中的核心部件，其开关和闭合的响应时间是影响喷雾精准性的重要因素之一[4-5]。目前以电磁阀结构、材料等为影响因素分析电磁阀动态响应特性的研究已较多[6-10]。研究发现，电磁阀本身的线圈匝数、气隙、电阻及弹簧预紧力等结构参数对电磁阀响应特性均有一定影响。但以电磁阀控制信号为影响因素的研究往往不能引起足够重视。相比普通PWM控制方式（在阀体保持阶段采用恒定PWM信号），改进型PWM控制方式（在阀体保持阶段采用高频PWM信号）可缩短电磁阀响应时间[11]，电磁阀响应时间为电磁阀开启响应时间和电磁阀闭合响应时间的和。

目前，Topçu等[12]对改进型PWM控制方式的优势进行了理论分析及论证，并以高速开关电磁阀为对象，针对驱动电压、保持电流及PWM频率等参数优化了电磁阀的开关特性；Messina等[13]建立了基于PWM电磁阀控制的气动执行器动态响应特性的数学模型，并分析了不同控制参数条件下电磁阀开关动作与电信号之间延时时间的变化情况；苏岭等[14]在保持其他PWM参数不变的情况下，分别对PWM频率、占空比、延迟时间等参数对电磁阀保持电流的影响进行了试验分析。但以上这些研究只针对独立变量，没有考虑变量之间是否存在交互作用。

响应面法在多因素系统中寻找最佳条件，克服了在正交试验中只能对单个孤立试验点进行分析且不够直观的缺点[15-16]，现已广泛应用于各类试验的参数优化中[17]。在实际喷雾植保作业中，考虑到电磁阀响应时间受到包括驱动电压、PWM延迟时间和PWM占空比在内的多个控制参数的影响，本文采用响应面法来获取一定参数范围内的电磁阀最短响应时间。

1 电磁阀响应时间的影响因素

为尽可能缩短电磁阀响应时间，需在阀芯动作时，使线圈产生较大的电磁力实现阀芯快速开关，而一旦完成动作后，仅需较小的电磁力保持阀芯状态。根据夏胜枝等[18]的推算，在假设磁路未饱和，且忽略铁损和磁路中导磁材料的磁阻的条件下，电磁阀的电磁力用如下方程表示为

式中Fmag为电磁阀的电磁力，N；u0为空气磁导率，H/m；i为线圈电流，A；N为线圈匝数；A为电磁作用面积，m2；δ为工作间隙，m。

由式（1）可知，对于同一电磁阀，在电磁阀的线圈匝数、气隙、电阻及弹簧预紧力等结构参数一定的情况下，电磁阀阀芯闭合前以及闭合后的保持阶段中，电磁力均只受到线圈电流的影响，苏岭等[14]研究发现，阀芯闭合时，初始电流受电磁阀驱动电压影响；在线圈保持阶段，电流受到PWM延迟时间、PWM占空比以及电磁阀驱动电压等多重因素的影响。

2 试验平台与试验方法

2.1 电磁阀响应时间优化试验平台

设计的电磁阀响应时间优化试验平台的总体结构如图1所示。

图1 电磁阀响应时间优化试验平台Fig. 1 Optimization experiment platform for response time of spray solenoid valve

试验平台以气泵为压力源，主要包括人机控制部分、供压稳压部分及PWM变量部分。其中人机控制部分主要由计算机、STM32F407控制器以及数字示波器（TDS1002B-SC型，Tektronix泰克有限公司）构成；稳压供压部分主要由药箱、安全阀、球阀、压力罐、压力传感器（WMB2012-HS型，杭州烨立工控有限公司）、单向阀、气泵、电动机以及压力表构成；PWM变量部分主要由电磁阀（Q22XD-1.2L型，天津云杰气动科技有限公司）和喷头（H-VV9515型，美国喷雾公司）构成。数字示波器上的2个通道分别用于获取压力数据及控制信号大小数据[19]。

2.2 电磁阀响应时间的获取

电磁阀响应时间可通过实测电磁阀驱动电流、分析喷雾瞬时压力变化或检测阀芯位置等方式进行获取，考虑到喷雾瞬时压力对于雾滴粒径、喷雾流量等喷雾指标参数密切相关，研究喷雾压力对于进一步研究喷雾指标参数更具意义，同时，由于电磁阀、压力传感器及喷头通过三通接头相连，三者间距较短，且测量过程中喷雾压力不变，因此喷雾和电磁阀动作间的液力延迟可以忽略，故本文通过分析喷雾瞬时压力的变化来获取电磁阀响应时间。根据数字示波器采集到的电压值，喷雾瞬时压力值的计算公式为

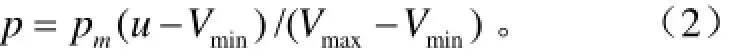
式中p为喷雾瞬时压力，MPa；pm为压力传感器量程大小，MPa；u为数字示波器采集的电压值，V；Vmin为压力传感器测量下限，V；Vmax为压力传感器测量上限，V。

运用卡尔曼滤波技术滤除传感器输出数据中的高斯白噪声可获取更准确的压力估值[19-20]。将喷雾系统压力设为0.14 MPa，控制脉冲的频率参数f设为5 Hz，占空比d设为50%，图2为经卡尔曼滤波器滤波前、后的PWM控制信号电压与喷雾瞬时压力的变化结果，对比显示，经滤波后，获取的压力数据更加可靠。

图2 经卡尔曼滤波器处理前后的波形数据Fig.2 Wave data before and after processing by Kalman filter

使用改进型PWM信号控制电磁阀时，适当的延迟时间使得开关电流足够高，阀芯的打开速度更快，之后高频的PWM控制信号产生的保持电流可维持阀芯的正常响应[11]。图3即为采用改进型PWM信号控制方法后的波形数据图。

考虑到过高的PWM脉冲频率可能对控制电路产生干扰[14]，故将高频时的PWM脉冲频率值设为定值10 kHz。设Pa和Pb分别表示电磁阀阀芯完全打开以及完全闭合时的喷雾瞬时压力值。图3中已标出电磁阀响应的临界时间点，图中t1为PWM控制信号产生的时刻，t2为喷雾压力达到Pa即电磁阀阀芯完全打开的时刻，t3为PWM控制信号消失的时刻，t4为喷雾压力达到Pb即电磁阀阀芯完全闭合的时刻。则电磁阀开启的响应时间为t2与t1的差，电磁阀关闭的响应时间为t4与t3的差。通过改变电磁阀驱动电压、PWM频率、占空比、延迟时间等参数产生的各种改进型PWM控制信号，可获取不同的电磁阀响应时间。

图3 采用改进型脉宽调制信号控制方法的波形数据Fig.3 Wave data by modified pulse width modulation control method

2.3 Box-Behnken试验设计

该研究采用三因素三水平BBD（box-behnken design，Box-Behnken设计）试验方法，通过研究一种改进型PWM控制信号并优化控制信号参数，实现缩短喷雾响应时间的目的。本研究是在喷雾系统压力一定的基础上进行的，针对喷雾系统压力等系统参数对喷雾响应时间的影响将在进一步研究中完善。选取改进型PWM控制参数中的电磁阀驱动电压、PWM延迟时间、PWM占空比为3个因素，分别记为X1、X2和X3。为清楚分析出这些因素与电磁阀各个响应阶段的关系，需对电磁阀开启响应时间、电磁阀闭合响应时间和电磁阀响应时间进行分别讨论，故以这3个响应时间为响应值，分别记为Y1、Y2、Y，并建立数学模型。试验中每个因素的低、中、高3个水平分别以-1、0和+1进行编码。使用下述二次多项式方程进行拟合[21]。

式中Y为响应值；β0为常数项；βi,βii,βij为回归系数；Xi, Xj为因素水平值；ei为误差；k为因素数，该研究中k=3。

依据电磁阀工作手册,电磁阀直流线圈正常工作允许的电压波动范围为±10%左右，本研究所用电磁阀额定电压为12 V，故取10～14 V为优化范围。依据基本的电磁理论如式（1），要保证电磁阀可靠的打开需有足够的电流驱动，经预试验发现，在10 V驱动电压条件下当PWM延迟时间低于15 ms时，电磁阀无法开启，因此选择15 ms作为下限，但若延迟时间过长，产生的过高电流会造成过强的续流效应，因此选择较小的延长时间65 ms为上限。为了保证电磁阀能够完成完整的吸合动作，选择5%作为改进型PWM占空比的下限，同时由于过高的占空比影响保持电流的大小，不利于电磁阀的闭合响应，选择较小的25%作为上限，具体参数取值如表1所示。

表1 试验因素和水平Table 1 Factors and levels

试验条件设置如下：电磁阀完全打开和闭合时的临界压力值Pa和Pb分别取0.12和0.01 MPa，喷雾系统压力设为0.14 MPa，PWM频率取5 Hz。基于表2所示的BBD设计表，进行15轮次试验并用Matlab 7.9软件对所获取的波形数据进行分析。

3 试验结果与讨论

分析得出的数据如表2所示，其中第1～12轮次为不同PWM参数控制条件下电磁阀响应时间的相应变化，第13～15轮次为3次重复的中心点试验，用于对模型进行误差分析。

表2 Box-Behnken试验设计与结果Table 2 Box-Behnken experimental design matrix and responses

3.1 模型拟合

使用SAS 9.1.3软件对表2中的试验数据进行回归分析，拟合得出电磁阀开启响应时间、电磁阀闭合响应时间和电磁阀响应时间的二次多项回归模型如下

式中Y1为电磁阀开启响应时间，ms；Y2为电磁阀闭合响应时间，ms；Y为电磁阀响应时间，ms；X1为驱动电压，V；X2为延迟时间，ms；X3为占空比，%。

需对该回归模型进行方差分析以验证它的适用性[22]。回归模型的方差分析和拟合参数分别如表3和表4所示。Pr>F值表明回归模型的显著程度，当“Pr>F”值小于0.05时，即表示该项指标显著。从表3的分析结果来看，3个回归模型的Pr>F值均小于0.001，显示该回归模型具有高度的显著性。模型失拟项表示模型预测值与试验测量值不拟合的概率，3个回归模型失拟项的Pr>F值均大于0.05，故模型失拟项不显著，说明模型选择合适。决定系数R2的大小决定了相关的密切程度，当R2越接近1时，表示相关的方程式参考价值越高，反之越低。如表4所示，回归模型的决定系数R2和调整决定系数略微不同，但均大于0.9，表明模型具有很好的相关度。变异系数CV是衡量各观测值变异程度的统计量，反映了模型的置信度，CV值越低则模型置信度越高。如表4所示，CV值（1.924、2.482和1.096）较小，因此认为该回归模型的拟合度较好。图4为响应时间预测值与试验测量值的对比，从图4中直观看出，测量值与预测值差别极小，同样印证了该模型具有一定的实际意义[23-27]。

表3 回归模型的方差分析Table 3 Analysis of variance of models

表4 回归模型的拟合参数Table 4 Fit Statistics for models

图4 电磁阀各响应时间预测值与测量值的对比Fig.4 Comparison between predicted and measured values of each response time

3.2 PWM参数对于电磁阀响应时间的影响

该研究运用响应面法优化改进型PWM信号控制参数以缩短电磁阀响应时间，并选取了电磁阀驱动电压、PWM延迟时间、PWM占空比等控制参数进行研究。图5为各因素对电磁阀响应时间影响的响应曲面，响应面显示出了这些过程参数对于响应时间的影响。

3.2.1 电磁阀驱动电压的影响

表3显示出驱动电压对于3个回归模型均有显著影响，从实际状况来看，一方面，电压为线圈提供能量，使其产生足够大的电磁力以快速克服弹力打开阀芯，另一方面，高电压产生的多余能量会阻碍电磁阀的闭合响应，式（4）与式（5）符合该实际状况。总体来讲，从图5及式（6）中可看出，在相同延迟时间条件下，电磁阀响应时间随着驱动电压的增大而缩短。但过高的驱动电压并不能明显提高电磁阀响应速度，而且易造成电路过载[28]。

3.2.2 PWM延迟时间的影响

表3显示PWM延迟时间对于电磁阀开启响应时间作用最为显著，式（4）与式（5）反映出延迟时间越长，电磁阀开启响应时间越短而闭合响应时间越长。延迟时间对电磁阀动作的实际作用效果与驱动电压类似，但从图5及式（6）中可观察到这种效果相对较弱。

3.2.3 PWM占空比的影响

根据表3，占空比对电磁阀开启响应时间的影响较小，对电磁阀闭合响应时间的影响较显著。根据式（5），占空比越大，电磁阀闭合响应时间越长。这与实际情况相吻合，占空比在延迟时间之后开始对电流大小产生作用，而此时电磁阀已完全开启，同时占空比越大，输入线圈的能量越多，线圈消耗电流的速度越慢，从而阻碍电磁阀的闭合响应。从图5及式（6）中可知，随着占空比的增大，电磁阀响应时间变长，但增长速度越来越小。

图5 各因素对电磁阀响应时间影响的响应曲面Fig.5 Response surfaces of factor effect on response time

3.2.4 各参数之间交互作用的影响

根据表3，Y2和Y模型中交互项X1X3的“Pr>F”值<0.05，表明电磁阀驱动电压和PWM占空比的交互作用对于电磁阀闭合响应时间和电磁阀响应时间具有显著影响。

3.3 最优PWM参数的确定

设置以下参数范围：1）电磁阀驱动电压10～14 V；2）延迟时间15～65 ms；3）占空比5%～25%，并将每个变量的取值根据范围分别划分成5级。在此参数范围内使用SAS 9.1.3软件对已验证的回归模型进行求解，得到的结果显示，使电磁阀响应时间最短的控制参数为：电磁阀驱动电压12 V，延迟时间15 ms，占空比5%，在此控制参数条件下，计算得到电磁阀响应时间可缩短至69.9 ms。

3.4 模型试验验证

通过试验对优化的控制参数进行测试，并与模型预测值进行对比，结果如表5所示。试验测得的电磁阀响应时间为69.7 ms，与预测值69.9 ms相比仅有0.29%的误差。同时经试验测得，在使用相同的电磁阀驱动电压12 V时，使用普通控制方法（在阀体保持阶段无高频PWM信号，即无延迟时间和占空比）测得的电磁阀响应时间为88.4 ms，经响应面法优化后的改进型PWM参数可将此电磁阀响应时间缩短21.2%，故可以得出该模型能够有效控制电磁阀的响应时间。

表5 响应时间的优化试验参数Table 5 Parameters of optimised experimental runs for response time

4 结论

本文采用响应面法优化改进型脉冲宽度调制（pulse width modulation, PWM）控制参数以缩短喷雾植保用电磁阀的响应时间。选取了电磁阀驱动电压

PWM延迟时间、PWM占空比为考察因素建立了关于电磁阀开启响应时间、闭合响应时间、响应时间的二次多项回归模型并进行了验证，分析了3个参数对这3种响应时间的影响。对电磁阀响应时间回归模型进行分析求解后得出，参数优化区间内使电磁阀响应时间最短的控制参数为：电磁阀驱动电压12 V，延迟时间15 ms，占空比5%，此时电磁阀响应时间为69.7 ms，与试验测量值基本一致。同时试验发现，与普通控制方式相比，经响应面法优化后的PWM参数可将电磁阀响应时间缩短21.2%，这表明使用改进型PWM控制信号并优化控制参数后对于缩短电磁阀响应时间是有效的。

[1] Vondricka J, Lammers P S. Evaluation of a carrier control valve for a direct nozzle injection system[J]. Biosystems Engineering, 2009, 103(1): 43－48.

[2] 傅泽田，祁力钧，王俊红. 精准施药技术研究进展与对策[J].农业机械学报，2007，38(1)：189－192. Fu Zetian, Qi Lijun, Wang Junhong. Developmental tendency and strategies of precision pesticide application techniques[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(1): 189－192. (in Chinese with English abstract)

[3] 魏新华，蒋杉. 农药变量喷施技术的研究现状及发展趋势[J].农机化研究，2011，33(2)：9－14. Wei Xinhua, Jiang Shan. The research status and development trend of pesticide variable-rate spray technique[J]. Journal of Agricultural Mechanization Research, 2011, 33(2): 9－14. (in Chinese with English abstract)

[4] Loghavi M, Mackvandi B B. Development of a target oriented weed control system[J]. Computers and Electronics in Agriculture, 2008, 63(2): 112－118.

[5] Han S, Hendrickson L L, Ni B, et al. Technical notes: Modification and testing of a commercial sprayer with PWM solenoids for precision spraying[J]. Applied Engineering in Agriculture, 2001, 17(5): 591－594.

[6] 范立云，许德，费红姿，等. 高速电磁阀电磁力全工况关键参数相关性分析[J]. 农业工程学报，2015，31(6)：89－96. Fan Liyun, Xu De, Fei Hongzi, et al. Key parameters’correlation analysis on high-speed solenoid valve electromagnetic force under overall operating conditions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(6): 89－96. (in Chinese with English abstract)

[7] 林义忠，曾德乐，冯喆. 基于 PWM 控制的高速开关电磁球阀动态特性仿真分析[J]. 机床与液压，2014，42(3)：152－154. Lin Yizhong, Ceng Dele, Feng Zhe. Simulation analysis of dynamic characteristics for high-speed switch electromagnetic ball valve based on PWM[J]. Machine Tool & Hydraulics, 2014, 42(3): 152－154. (in Chinese with English abstract)

[8] 刘鹏，范立云，白云，等. 高速电磁阀电磁力近似模型的构建与分析[J]. 农业工程学报，2015，31(16)：96－101. Liu Peng, Fan Liyun, Bai Yun, et al. Modeling and analysis of electromagnetic force approximate model of high-speed solenoid valve[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(16): 96－101. (in Chinese with English abstract)

[9] Kajima T, Kawamura Y. Development of a high-speed solenoid valve: investigation of solenoids[J]. Industrial Electronics, IEEE Transactions on, 1995, 42(1): 1－8.

[10] Passarini L C, Nakajima P R. Development of a high-speed solenoid valve: An investigation of the importance of the armature mass on the dynamic response[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2003, 25(4): 329－335.

[11] Taghizadeh M, Ghaffari A, Najafi F. Modeling and identification of a solenoid valve for PWM control applications[J]. Comptes Rendus Mecanique, 2009, 337(3): 131－140.

[12] Topçu E E, Yüksel İ, Kamış Z. Development of electro-pneumatic fast switching valve and investigation of its characteristics[J]. Mechatronics, 2006, 16(6): 365－378.

[13] Messina A, Giannoccaro N I, Gentile A. Experimenting and modelling the dynamics of pneumatic actuators controlled by the pulse width modulation (PWM) technique[J]. Mechatronics, 2005, 15(7): 859－881.

[14] 苏岭，柳泉冰，汪映，等. 脉宽调制保持电磁阀驱动参数的研究[J]. 西安交通大学学报，2005，39(7)：689－692. Su Ling, Liu Quanbing, Wang Ying, et al. Experimental investigation on parameters of pulse width modulation-holding solenoid valve drive mode[J]. Journal of Xi’an Jiaotong University, 2005, 39(7): 689－692. (in Chinese with English abstract)

[15] Myers R H. Response surface methodology-current status and future directions[J]. Journal of Quality Technology, 1999, 31(1): 30.

[16] 张泽志，韩春亮，李成未. 响应面法在试验设计与优化中的应用[J]. 河南教育学院学报：自然科学版，2011，20(4)：34－37. Zhang Zezhi, Han Chunliang, Li Chengwei. Application of response surface method in experimental design and optimization[J]. Journal of Henan Institute of Education (Natural Science Edition), 2011, 20(4): 34－37. (in Chinese with English abstract)

[17] 王永菲，王成国. 响应面法的理论与应用[J]. 中央民族大学学报：自然科学版，2005，14(3)：236－240. Wang Yongfei, Wang Chengguo. The application of response surface methodology[J]. Journal of the Central University For Nationalities: Natural Science Edition, 2005, 14(3):236－240. (in Chinese with English abstract)

[18] 夏胜枝，周明，李希浩，等. 高速强力电磁阀的动态响应特性[J]. 清华大学学报：自然科学版，2002，42(2)：258－261. Xia Shengzhi, Zhou Ming, Li Xihao, et al. Dynamic response characteristics of high-speed, powerful solenoid valve[J]. Journal of Tsinghua University: Science and Technology, 2002, 42(2): 258－261. (in Chinese with English abstract)

[19] 蒋焕煜，周鸣川，童俊华，等. 基于卡尔曼滤波的PWM变量喷雾控制研究[J]. 农业机械学报，2014，45(10)：60 －65. Jiang Huanyu, Zhou Mingchuan, Tong Junhua, et al. PWM variable spray control based on Kalman filter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(10): 60－65.(in Chinese with English abstract)

[20] Maatje K, De M R M, Rossing W. Cow status monitoring (health and oestrus) using detection sensors[J]. Computers and Electronics in Agriculture, 1997, 16(3): 245－254.

[21] Yazgi A, Degirmencioglu A. Optimisation of the seed spacing uniformity performance of a vacuum-type precision seeder using response surface methodology[J]. Biosystems Engineering, 2007, 97(3): 347－356.

[22] Omwamba M, Hu Q. Antioxidant capacity and antioxidative compounds in barley (Hordeum vulgare L.) grain optimized using response surface methodology in hot air roasting[J]. European Food Research and Technology, 2009, 229(6): 907－914.

[23] Li Quanhong, Fu Caili. Application of response surface methodology for extraction optimization of germinant pumpkin seeds protein[J]. Food Chemistry, 2005, 92(4): 701－706.

[24] Karunanithy C, Muthukumarappan K. Influence of extruder and feedstock variables on torque requirement during pretreatment of different types of biomass: A response surface analysis[J]. Biosystems Engineering, 2011, 109(1): 37－51.

[25] Rožić L, Novaković T, Petrović S. Modeling and optimization process parameters of acid activation of bentonite by response surface methodology[J]. Applied Clay Science, 2010, 48(1): 154－158.

[26] Beg Q K, Sahai V, Gupta R. Statistical media optimization and alkaline protease production from Bacillus mojavensis in a bioreactor[J]. Process Biochemistry, 2003, 39(2): 203－209.

[27] Li Yin, Liu Zhiqiang, Zhao Hui, et al. Statistical optimization of xylanase production from new isolated penicillium oxalicum ZH-30 in submerged fermentation[J]. Biochemical Engineering Journal, 2007, 34(1): 82－86.

[28] 张廷羽，张国贤. 高速开关电磁阀的性能分析及优化研究[J].机床与液压，2006(9)：139－142. Zhang Tingyu, Zhang Guoxian. Performance analysis and investigation to high speed digital valve[J]. Machine Tool & Hydraulics, 2006(9): 139－142.(in Chinese with English abstract)

Optimization for response time of solenoid valve through response surface methodology

Jiang Huanyu, Zhang Lijun, Zhou Mingchuan, Shi Weinan
(College of Biosystems Engineering and Food Science, Zhejiang University, Hangzhou 310058, China)

Solenoid valve driven by PWM (pulse width modulation) control signal is used as interface between electronic control and fluid flow in precision spraying, the response time of which has huge impact on the performance of precise spray system. Longer response time would reduce the accuracy of spraying and increase the overuse of chemical. A modified PWM technology (with much higher frequency for controlling the holding current) was applied and 3 parameters of PWM control signal containing driving voltage, delayed time and duty cycle were optimized by RSM (response surface methodology) to shorten the response time, which was composed of opening response time and closing response time. The optimization of parameters was carried out through the BBD (Box-Behnken design) with 3 factors and 3 levels. The critical factors (and their values) selected for the research were driving voltage (10, 12 and 14 V), delayed time (15, 40 and 65 ms) and duty cycle (5%, 15% and 25%). In order to better explore the influence of factors on each response phase of solenoid valve, the opening response time, closing response time and response time were discussed separately. The experiment was performed on an optimization experiment platform which consisted of human-machine control module, pressure supply module and PWM module. On the platform, the wave data that could reflect the relation between voltage of PWM control signal and instantaneous spray pressure near the nozzle were acquired through digital oscilloscope and then processed by Kalman filter. By analyzing the wave data, the opening and closing response time of solenoid valve with different parameters were calculated. After 15 runs of experiments under different parameter conditions, the mathematical regression models for the opening response time, closing response time and response time were built, respectively. Then the models were tested by the analysis of variance and statistical parameters of the model for response. The test indicated that the relations between response variables and independent variables were significant and the regression models were thought to be appropriate. Through the analyses of 3 tested models and response surfaces showing the effects of process parameters on response time, the effects of driving voltage, delayed time and duty cycle of PWM signal on 3 kinds of response time of solenoid valve were obtained. Firstly, the voltage had a significant effect on all response models and a positive effect on reducing response time. Secondly, the delayed time had a negative effect on reducing response time and the effect it brought was not so significant; in addition, longer delayed time could accelerate the opening phase but detain the closing phase. Thirdly, the duty cycle had a negative effect on reducing response time and had more remarkable influence on the closing response time than opening response time. Lastly, the interaction between driving voltage and duty cycle on closing response time was significant. After that, the optimal control parameter combination for the minimum response time of solenoid time was obtained by analyzing the regression model of response time, which was 12 V voltage for driving solenoid, delayed time of 15 ms and duty cycle of 5%. The predicted optimal control parameters were tested in the laboratory using the modified PWM control method and normal PWM control method which had stable voltage, respectively. The results showed that the measured value by the modified PWM control method was very close to the predicted value and 21.2% of response time could be reduced compared to the normal control method. The result indicates that the RSM is useful for optimizing the parameters of modified PWM control signal to improve the response characteristics of solenoid valve.

valves; optimization; models; response surface methodology; agricultural spraying; response time; solenoid valve

10.11975/j.issn.1002-6819.2016.09.010

TP211

A

1002-6819(2016)-09-0067-07

蒋焕煜，张利君，周鸣川，施玮囡. 基于响应面法的电磁阀响应时间优化[J]. 农业工程学报，2016，32(9)：67－73.

10.11975/j.issn.1002-6819.2016.09.010 http://www.tcsae.org

Jiang Huanyu, Zhang Lijun, Zhou Mingchuan, Shi Weinan. Optimization for response time of solenoid valve through response surface methodology[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 67－73. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2016.09.010 http://www.tcsae.org

2015-08-10

2016-03-08

国家高技术研究发展计划（863计划）（2012AA10A504）；农业部引进国际先进农业科学技术（2011-G32）；浙江省“新世纪151人才工程”

蒋焕煜，男，浙江宁海人，教授，博士生导师，主要从事农业装备智能化技术与机器人方面的研究。杭州 浙江大学生物系统工程与食品科学学院，310058。Email：hyjiang@zju.edu.cn

·农业水土工程·