整体把握方差教学

赵存宇

(北京市朝阳区八十中学，北京 100102)



整体把握方差教学

赵存宇

(北京市朝阳区八十中学，北京 100102)

教学内容分析从整体把握的角度出发，进行数学概念教学时，我们应该首先引导学生认识此概念在整个数学理论体系中的地位，以及在实际应用中的价值，具体来说，方差是概率论和数理统计的重要概念之一，数据的方差是反映样本数据分布的数字特征，而随机变量的方差是反映随机变量取值分布的特征数．学习方差将为今后学习概率统计知识做铺垫．同时，它在市场预测、经济统计、风险与决策等领域有着广泛的应用．

其次，引导学生从教学目标设定、教学过程实施和教学结果评价这个整体的角度，去看待相关概念的学习．从近几年的高考情况看，本节是高考的热点内容之一，连续三年以解答题的形式出现．试题联系实际，设问新颖，突出考查学生对概念本质的理解，注重直观理解和归纳猜想，淡化纯粹的代数运算，体现了新课程改革下考试对教学的正向引领作用．

最后，应该引导学生从研究问题的方法这个高度去学习具体的知识，因此，在教学时，一方面引导学生重视概念理解，避免死记硬背，避免过分模式化的训练，将课堂定位于让学生作为主体在问题分析、探究和解决的过程中加强理解、提高能力．另一方面，强调直观感觉和归纳猜想之后的理性分析过程，做到有理有据．

学情分析对学生学情的整体把握体现在如下两个方面：首先，应该把握学生在小学、初中、高中整个学习过程中对相关知识的认知程度，学生在初中已经学习过数据的方差，高中又进一步学习了用样本的数字特征估计总体的数字特征以及随机变量的方差，而且已经做了复习．其次，从学生知识、能力和思维方法的整体框架下评估学生的当前水平，学生知道方差的定义，对方差的含义有基本的了解，会解决一些基本的问题，但理解比较肤浅，还停留在感觉的层面，缺少理性的分析做支撑．本节授课班级是理科普通班，学生有一定基础，但不够扎实．

教学目标

1.能说出数据方差的定义公式，能准确理解方差的含义并利用其比较两组数据的方差大小．

2.经历研究问题的过程，体会从特殊到一般的思想，提高通过演绎推理进行验证的意识．

3.通过创设情境激发学生探究问题的兴趣，在学生分析问题、解决问题的过程中培养其积极探索的精神，培养严谨治学的态度．

教学重点 通过解决估计方差大小等相关问题，进一步准确深入理解方差的含义．

教学难点 从直观感觉深化为理论分析．

教学方法 引导探究．

教具 多媒体设备．

学法指导

注重发挥学生的主体性，让学生在问题探究过程中澄清概念，加深理解，并学会怎样发现问题、分析问题和解决问题．

教学过程

一、创设情境引出课题

教师活动：前面我们已经复习了数据的方差，请回顾概念，完成如下填空：

(2)方差描述了样本数据的大小，反映了样本数据到________的一种平均距离．

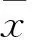
学生活动：回顾概念，完成填空．

设计意图：回顾基本概念，完成知识提取过程．

教师活动：我们对方差的概念和含义已经有了一定程度的理解，请尝试完成如下问题．

引例(2013年全国高考北京卷理科文科)

下图是某市3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择3月1日至3月15日中的某一天到达该市，并停留2天．

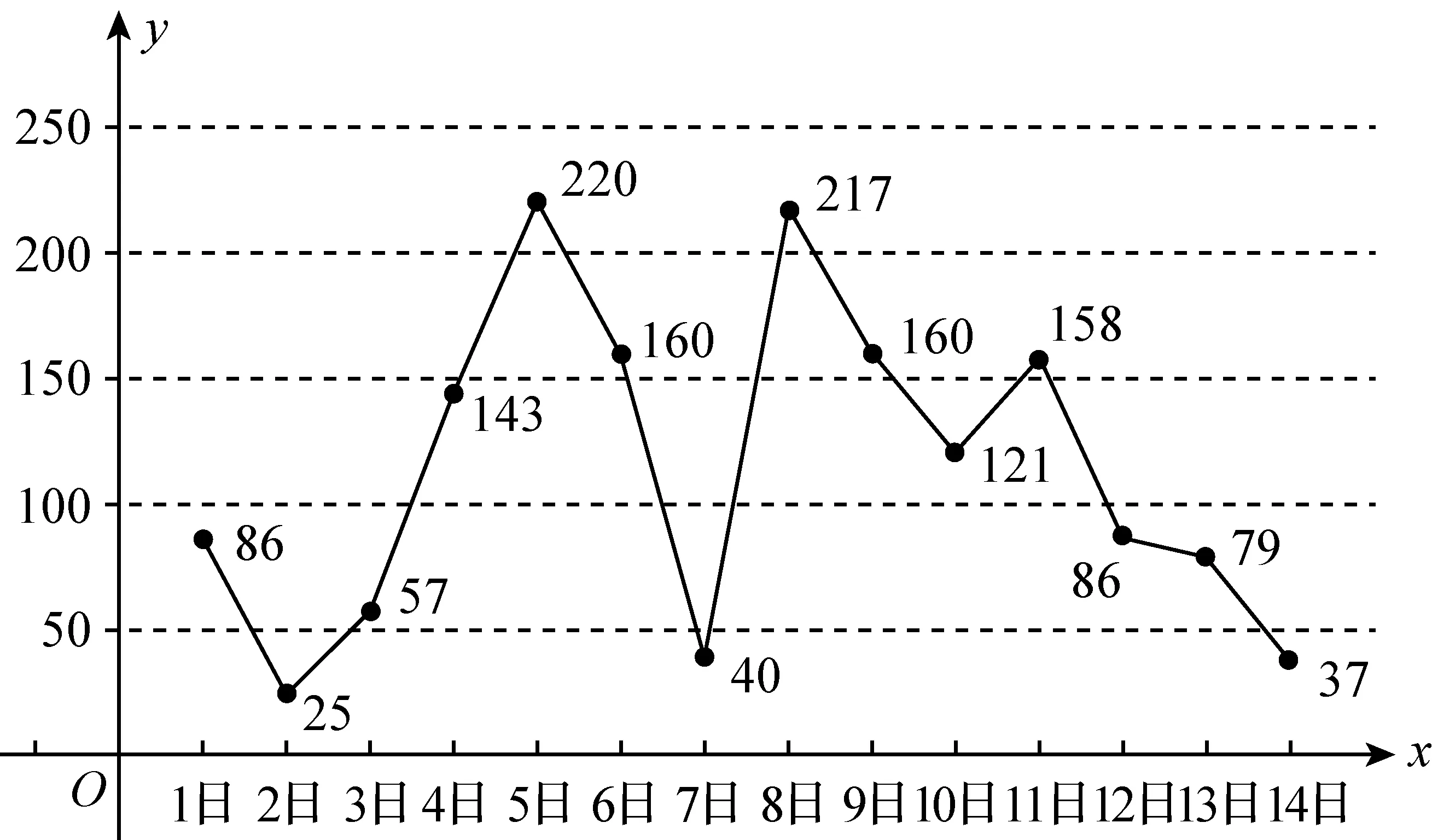
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大？(结论不要求证明)

设计意图：以最近的高考题为例提出问题，激发学生解决问题的兴趣，引出课题，从一个侧面让学生体会所学内容的重要性．

二、分析思路展开探究

问题1 需要比较多少组数据？每组数据由几个数构成？

设计意图：引导学生分析题意，认清要比较的对象．

将第1天开始连续三天的数据记为第1组，第2天开始连续三天的数据记为第2组，以此类推，直到第12天开始连续三天的数据记为第12组，共12组数据，每组数据有3个数．

问题2 你认为哪组数据方差最大？请说出你的判断依据．

学生活动：学生思考，寻找解决问题的切入点．

预设回答：

(1)计算出每连续三天的方差，然后比较．

教师活动：你如何评价这种思路？

计算出每组的方差是一种非常直接的方法，但对于问题共需比较12组数据的方差，每组数据有3个数．如果有信息技术的辅助，可以很快地得到结果，但如果没有技术手段，则会因计算量太大而几乎无法进行．那么如何结合已有知识，寻找运算量更小，更行之有效的方法呢？

设计意图：数学中的很多问题表面上有很直接的方法，但如果不借助于信息技术等辅助手段，这些方法会因为太过复杂或计算量太大而缺乏可行性，这时应引导学生通过对问题的深入分析，寻找更可行的方法．

(2)比较极差

教师活动：对于两组数据，极差大的一组数据其方差一定大吗？

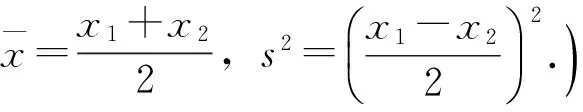
A：0，0，9；

B：0，5，10．

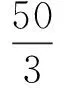
设计意图：极差和方差都是描述数据离散程度的数字特征，但二者并不等价，应该帮助学生澄清这一问题．

(3)按照对方差含义的理解，方差描述数据波动的大小，因此第6组数据(第6天开始连续三天的数据)方差大．

教师活动：你同意这种对方差的理解方式吗？

比较第5组和第6组数据，事实上第5组方差更大，可见数据的方差描述的是数据偏离均值的离散程度，不能理解为日常生活中按时间顺序或数据顺序的“波动”大小，例如股票随时间的波动等，即样本的方差与样本中数据的排列顺序无关．

设计意图：注意引导学生对方差含义的正确理解．

(4)根据对方差含义的理解，方差描述的是数据偏离均值的离散程度，感觉应该选第5组数据．

教师活动：从直观感觉以及对方差含义的理解，我们选择第5组数据，能更清晰地说明你的依据吗？从比较第5组和第6组数据过程中，你能得到哪些启发？

学生活动：这两组数据的特点是有两个数相同，第三个数不同，因此我们可以考虑如下问题．

探究一

问题3 对3个数据x1,x2,x3构成的样本，考虑当x1,x2固定，改变x3时方差的大小如何变化？

教师活动：我们先通过一个具体的例子入手，并注意从中提炼更一般的规律．

例1 下列各种数据中，

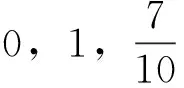
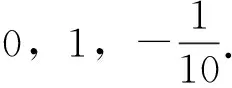
方差从大到小的顺序是____________．

学生活动：学生通过画散点图或对方差含义的理解，解决这一具体例子，并尝试从中归纳更一般的结论．

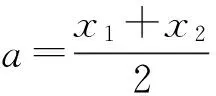
直观解释：如果x3离x1,x2的中点越远，则s2越大．

证明：设三个数分别为x1,x2,a+x，求s2的表达式，并完成证明．

事实上有

将结论推广至多个数据的情形，并证明你的猜想：

推论1 对n个数据x1,x2,…,xn，其中x1,x2,…,xn-1固定，记

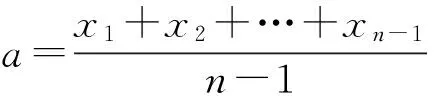
设计意图：教会学生如何分解困难的任务，先提出较简单的情形，即探究一的问题．通过解决具体的例子，归纳猜想更一般性的结论，并注意加以验证．既提高学生的合情推理能力，也注意培养学生严谨的治学态度．同时，让学生体会如何用函数的思想解决与变化相关的问题．

学生活动：分析引例可知，相邻的两组数据都符合结论1的条件，因此，利用结论1完成相应数据方差的比较．

通过比较，我们可以得到如下结果：

第1组方差<第2组方差第2组方差<第3组方差第3组方差>第4组方差第4组方差<第5组方差第5组方差>第6组方差第6组方差=第7组方差第7组方差>第8组方差第8组方差>第9组方差第9组方差<第10组方差第10组方差<第11组方差第11组方差>第12组方差

由此可知，我们只需比较第3组、第5组和第11组的方差．

观察数据可知，第3组和第5组数据有一个数相同，而且两组数据的平均数一样，因此我们提出如下问题．

探究二

问题4 对3个数据x1,x2,x3，当x1固定，x2+x3固定，即三个数平均数固定，改变x2和x3时方差的大小如何变化？

教师活动：我们仍然从一个具体的例子入手，并注意从中提炼更一般的规律．

例2 下列各组数据中，

A.1,3,5；B.1,4,4；

C.1.9,1,6.1；D.1,0,8．

方差从大到小的顺序是____________．

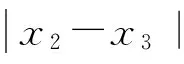
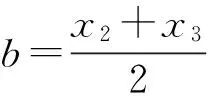
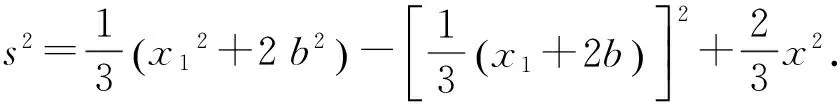
将结论2推广至多个数据的情形，并加以证明：

设计意图：考虑一组数据中,保持均值不变的前提下，改变其中两个数据时方差大小的变化．

分析引例可知，

第3组方差<第5组方差

最后，我们只需比较第5组数据和第11组数据的方差即可，前面我们知道极差大的样本，方差不一定大，但这两组数据的极差相差很大，直观上感觉第5组数据的方差大于第11组数据的方差，你能严格说明吗？

探究三

问题5 对包含有3个数据的样本，极差和方差之间有怎样的联系？

例3 完成下列问题

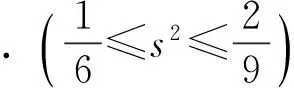
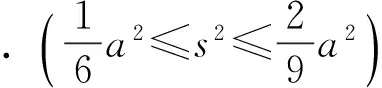
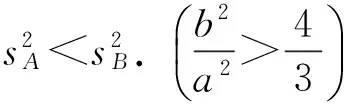
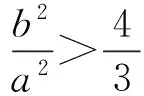
设计意图：极差和方差相比较而言，极差更简单，更易于计算，因此如果能由极差的大小去估计方差的大小，则问题会大大简化，对三个数据而言，我们在一定程度上可以做这种估计，但对于更多的数据，这种估计的实际意义将变得很小．同时，让学生体会不等式的思想．

分析引例可知，第5组数据的极差是180，第11组数据的方差是79，由结论3可知,

第5组方差>第11组方差

至此，我们知道第5组数据的方差最大．

设计意图：通过观察、猜想和实验验证数据改变对方差大小的影响，深化对数据方差的含义的理解．

三、深化认识巩固练习

变式练习假设有三个非负实数a,b,c,其中a>0，a+b+c=600．当数据a,b,c的方差s2最大时，写出

a,b,c的值(结论不要求证明)，并求此时s2的值．

四、课堂小结回顾收获

1．通过本节课的学习，在知识和技能方面你有哪些提高？

2．在研究问题过程中，你收获了哪些思想和方法？

3．通过本课题的探究，你觉得研究问题一般要经历哪些步骤？

4．你觉得本节课的哪些方面比较有意思，或者比较重要？

五、课后练习加深理解

1.(1)对4个数据0,x,y,1，其中0≤x≤1，0≤y≤1，则x,y为何值时，s2最大？(结论不要求证明)

(2)对5个数据，你能提出类似于(1)中的问题并给出解答吗？

(3)从(1)和(2)出发，你能归纳出更一般的结论吗？

2.随机变量X服从如下两点分布：

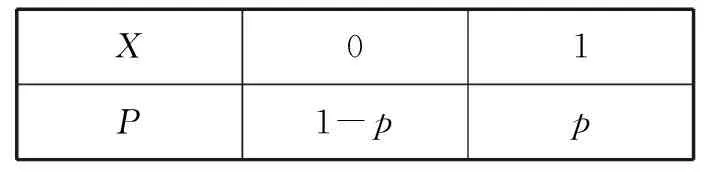
X01P1-pp

当p为何值时，D(X)达到最大？

(责任编辑：李 珺)