利用轴对称变换求最短路径问题
2016-12-19浙江省宁波市鄞州区集士港镇中学董方泽
□浙江省宁波市鄞州区集士港镇中学 董方泽
利用轴对称变换求最短路径问题
□浙江省宁波市鄞州区集士港镇中学 董方泽
【课本原型】浙教版八上书本P50例2。如图,直线l表示草原上的一条河流。一骑马少年从A地出发,去河边让马饮水,然后返回位于B地的家中。他沿怎样的路线行走,能使路程最短?作出这条最短路线。

解法:作点B关于直线l的对称点B′,连结AB′,与直线l相交于点P,连结BP。骑马少年沿折线A-P-B的路线行走时路程最短。
证明:如图,在直线l上任取一点P′(与点P不重合),连结AP′,BP′,B′P′.
由轴对称的性质知,BP=B′P,BP′=B′P′
∴AP+BP=AP+B′P=AB′,AP′+BP′=AP′+B′P′
在△AB′P′中,AB′<AP′+B′P′
∴AP+BP<AP′+BP′。
即AP+BP最短。
“最短路径问题”的原型就来自于“饮马问题”,要解决这一问题,是利用作对称点把折线问题转化成直线问题,它离不开构建与转化“两点之间,线段最短”的数学公理。在日常生活、工作中,也经常会遇到有关行程路线的问题,我们把这类求近道的问题统称最短线路问题,出题者通常以直线、角、三角形、特殊四边形、坐标轴等对称图形为背景。本文就在“最短路径”中探寻一番,举例分析,帮助同学们学习。
【迁移与拓展】
1.一点两线(相交)解决周长最短。
如图所示,点P为一处马厩,ON为草原的边缘(下方为草原),OM为一条河流。清晨,骑马少年要从马厩牵马先去草地吃草,然后到河边饮水,最后再回到马厩。请帮他设计一条最近的行走路线。
解析:依据两点之间线段最短,可分别作点P关于OM,ON的对称点分别为P1、P2,连P1P2交OM、ON于点A、B。此时ΔPAB的周长PA+PB+AB=P1P2为最小。(证明略)

2.二点两线(相交)解决周长最短。
如图所示,P为帐篷,Q为马厩,骑马少年某天要从马厩牵出马,先到草地边ON的某一处牧马,再到河边OM饮水,然后回到帐篷,请你帮他确定这一天的最短路线。
解析:如图分别作点P、Q关于OM,ON的对称点为P′、Q′,连P′Q′,交OM、ON于点A、B。此时四边形PABQ的周长PA+AB+BQ+PQ=P′Q′为最小。(证明略)
3.一点两线(相交)解决距离之和最短。
如图所示,A为马厩,骑马少年某天要从马厩牵出马,先到河边OM的某处P饮水,再到草地ON边某处B牧马,请你帮他设计一条路线,使AP+BP最短。
解析:如图作点A关于OM的对称点A′,过A′作ON的垂线交OM于P,交ON于B,则A→P→B为最短路线。(证明略)
【应用与延伸】

1.如图,一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4),?O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点坐标。
解析:作点C关于y轴的对称点C',连接C'D,交y轴于点P则C'D=C'P+PD=PC+PD。C'D就是PC+PD的最小值,连接CD,则CD=2,CC'=2。在直角△C'CD中,根据勾股定理C'D=2求直线C'D的解析式,由C'(-1,0),D(1,2)得y=x+1当x=0时,y=1,则P(0,1)。
2.如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,△APD中边AP上的高为__。

解析:作点A关于BC的对称点A',连接A'D,交BC于点P,则A'D=PA'+PD=PA+PD,A'D的长就是PA+PD的最小值。△APD的面积为4。在直角△ABP中,AB=4,BP=1,根据勾股定理得,AP上的高为
3.如图,已知⊙O的直径CD为4,∠AOD的度数为60°,点B是弧AD的中点,在直径CD上找一点P,使BP+AP的值最小,并求这个最小值。
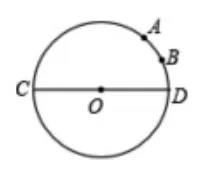
解析:作点A关于CD的对称点A',连接A'B,交CD于点P,则A'B的长就是PA+PB的最小值。连接OA',OB,则∠A'OB=90°,OA'=OB=4根据勾股定理

解析:作点B关于AD的对称点B',过点B'作B'E⊥AB于点E,交AD于点F,则线段B'E的长就是BM+MN的最小值在等腰Rt△AEB'中,根据勾股定理得到:B'E=4。
课本原型的饮马问题,实质上是线段之和最短的问题。既然是线段之和,自然从最初的两条线段、演变到后来的三更多条线段之和的最短问题。饮马问题是一种让我们更深入观察和分析知识的重要角度。我们要注重知识的延伸和迁移,使学生在学与练的过程中体味数学的奇妙。
