GV-半群的矩形群同余

王 宇

(安徽理工大学 理学院，安徽 淮南 232001)



GV-半群的矩形群同余

王 宇

(安徽理工大学 理学院，安徽 淮南 232001)

利用GV-半群中元素的弱逆和核-超迹的方法,通过建立矩形同余对来描述GV-半群的矩形群同余的性质，并给出矩形群同余的一个表示．

GV-半群；矩形群同余；弱逆；自共轭

半群是一个满足结合律的二元运算的代数系统.在一个多世纪的半群代数理论历史中，对正则半群的研究一直占主导地位.近三十年，对非正则半群的研究引起代数学者的重视．GV-半群是广义的完全正则半群，因此，它是与完全正则半群性质最为接近的非正则半群．研究毕竟正则半群的最常用方法就是把正则半群中已知结果推广到毕竟正则半群中．同余是正则半群研究中的一个重要工具，并已取得广泛的结果，核-迹方法是正则半群中研究同余的一个重要方法，Gomes发展了核-迹方法而定义了核-超迹方法．罗彦锋教授使用这种方法在毕竟正则半群中研究同余．本文就是利用核-超迹方法来研究GV-半群的矩形群同余．首先，给出文中所需要的基本概念和定义．

1 基本概念及定义

半群S称为毕竟正则半群，若S的每个元素a都存在一个整数幂n，使得an是正则的．半群S称为GV-半群,如果S是毕竟正则的，且S中每一正则元都是完全正则的；半群S的元素x称为a的弱逆，若xax=x,a∈S，用W(a)表示S中所有a的弱逆的集合，半群S称为矩形群，若S是正则半群，且ES是矩形带．半群S上的同余称为矩形群同余，若S/ρ是矩形群．设ρ是半群S的同余，定义S的子集{a∈S|aρ⊆E(S/ρ)}为ρ的核，记作kerρ．把ρ限制在上称为ρ的超迹，记为htrρ．以下文中如没有特别说明S均指GV-半群．

定义1 S的一个子半群K称为正规的，若

(1)a∈K,a′∈W(a)⟹a′∈K；

(2)ES⊆K；

(3)a∈S,a′∈W(a)⟹aKa′,a′Ka⊆K．

定义2 S的子半群上的同余ε称为正规的，若对任意x,y∈，a∈S和a′∈W(a)，有xεy⟹axa′εaya′，a′xaεa′ya,其中axa′，aya′,a′xa,a′ya∈.

定义3 设ε是上的正规同余，且/ε是矩形带，K是S的正规子半群，则(ε,K)称为S的矩形同余对，若它满足：

(RCP1)∀a∈S,a′∈W(a)，则存在a″∈W(a)，使得aa″aa′εaa′，a′aa″aεa′a；

(RCP2)∀a∈S,x∈且xa∈K⟹a∈K．

下面在S上定义一个二元关系

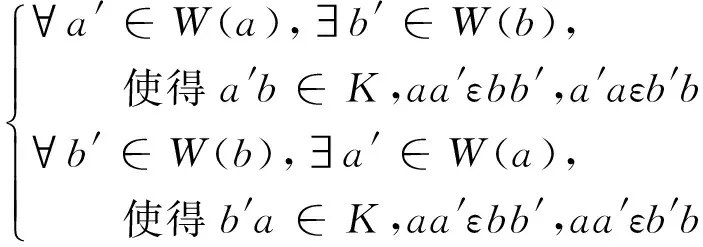
2 主要结论

以下用RC(S)表示S上所有的矩形群同余集合，用RCP(S)表示S上所有的矩形群同余对集合．首先给出本文的主要结果．

定理1 设S是GV-半群．若(ε,K)∈RCP(S)，则ρ(ε,K)∈RC(S)且kerρ(ε,K)=K和htrρ(ε,K)=ε．

证明定理1需要证明下面四个命题．在下面的证明中令ρ=ρ(ε,K)，若(ε,K)∈RCP(S)．

命题1 若(ε,K)∈RCP(S)，且∀a,b∈K．∀x∈.如果ab∈K，则axb∈K且ρ是S的等价．

证明 设ab∈K，∀a,b∈S,则a′aba∈K，∀a′∈W(a)．由(RCP2)，可得ba∈K，a′a∈，又(ba)x∈K，∀x∈和b′baxb∈K,∀b′∈W(b)，则由(RCP2)知axb∈K．ρ满足对称性．又因ES⊆K和ε是自反的，故ρ是自反的．

下证ρ满足传递性．设aρb,bρc，则对∀a′∈W(a)，存在b″∈W(b)，使得a′b∈K,aa′εbb″,a′aεb″b．对∀b′∈W(b),存在c′∈W(c),使得b′c∈K,bb′εcc′,b′bεc′c．则由ε的传递性可得，aa′εcc′,a′aεc′c．令g∈M(aa′,bb′) ．则由K是正规的和a′b∈K，可得b′ga∈W(a′b)⊆K．又因a′bb′ga∈ES⊆K,a′bb′c∈K和gaa′∈，即得a′bb′(gaa′)c∈K，因而由(PCP2)，即得a′c∈K．另一方面，同理可知对∀c′∈W(c)，存在a′∈W(a)，使得c′a∈K,aa′εcc′，a′aεc′c，故aρc，因此ρ是S上的一个等价．

命题2 若(ε,K)∈RCP(S)，则ρ是S上的同余．

证明 先证ρ是左相容的．设aρb，a,b∈S,对∀(ca)′∈W(ca)，有a′=(ca)′c∈W(a),c′=a(ca)′∈W(c),(ca)′=a′c′,aa′=cc′．由aρb即知(ca)′cb=a′b∈K．又由ρ的定义，可知存在b′∈W(b)，使得aa′εbb′又存在g∈M(aa′,bb′)=M(c′c,bb′)，使得c′c=aa′εgεbb′．设(cb)′=b′gc′，则(cb)′=b′gc′∈W(cb)．同理可得，对∀(cb)′∈W(cb)，存在(ca)″∈W(ca)，使得(cb)′ca∈K，ca(ca)″εcb(cb)′，(ca)″caε(cb)′cb，则caρcb．故ρ是S上的左同余．另一方面，同理可证ρ是S上的右同余，因此，ρ是S上的同余．

命题3 设(ε,K)∈RCP(S)，则htrρ=ε，且ρ(ε,K)是S上的矩形群同余．

证明 首先证htrρ=ε．设xρy,x,y∈，又存在x′∈W(x)∩，使得xεxx′x(ε是上的矩形带同余)．又由ρ的定义知存在y′∈W(y)∩，使得xx′εyy′，x′cεy′y，因此xεxx′xεyy′xεyx和yεyy′y(ε是上矩形带同余).又εyx′x,cεy′y则xεy，即htrρ⊆ε．

反之，设xεy,x,y∈，∀x′∈W(x)∩,因此x′y∈⊆K,x′yx′εx′xεx′(ε是上的矩形带同余)，即x′ε∈W(yε)．存在y′∈W(y)∩，使x′εy′，则xx′εyy′,x′xεy′y．同理，对∀y′∈W(y)，则存在x′∈W(x)，使得y′x∈K,xx′εyy′,x′xεy′y，故xρy，即ε⊆htrρ，因此htrρ=ε．

下证ρ=ρ(ε,K)是S上的正则同余．由(RCP1)知，对∀a∈S,a′∈W(a)，存在a″∈W(a)，使得a′aa″a∈K,a′aa″aa′aεa′aa′a=a′a，即(a′a)ε∈W((a″a)ε)．存在(a″a)∈W(a″a)∩，使(a″a)′εa′a．又因(a″a)′(aa″a)(a″a)′a′ρ(a″a)′(a″a)′a″a(a″a)′a′=(a″a)′(a″a)′a′ρ(a″a)′a′

(/ε是矩形带且htrρ=ε)

即((a″a)′a′)ρ∈W((aa″a)ρ)．存在(aa″a)′∈W(aa″a)，使得(aa″a)′ρ(a″a)′a′，

则aa″a(a″a)′ρaa″a(a″a)′a′ρaa″aa′aa′=aa″

aa′εaa′(由RCP1)

即aa″a(aa″a)′εaa″aa′εaa′．因htrρ=ε，且

(aa″a)′aa″aρ(a″a)′a′aa″aρa′aa′aa″a=a′aa″

aεa′a(由RCP1)

即(aa″a)′aa″aεa′aa″aεa′a(因htrρ=ε)．

另一方面，对∀c∈W(aa″a),ca∈W(a″a)，ac∈W(aa″)∈⊆K,

又因caa″a(ca)caa″aεcaa″a(因/ε是矩形带)，即(caa″a)ε∈W((ca)ε)，又因存在x∈W(ca)∩，使得xεcaa″a．令a′=xc，则a′∈W(a)，a(xc)εaa″axc(因RCP1)εaa″acaa″acε(aa″a)c．

并且同理可得(xc)aεc(aa″a)，因此aρaa″a．所以ρ是S上的正则同余．下面设aρ,bρ∈E(S/ρ)，则存在e,f∈ES，使aρe,bef，因/ε是矩形带，故efeρe，则(aba)ρa，即S/ρ是矩形群，因而ρ是S上的矩形群同余

命题4 若ρ是S的矩形群同余，则(htrρ,kerρ)是S上的矩形群同余对且ρ=ρ(htrρ,kerρ)．

证明 由矩形群同余对定义只需证(htrρ,kerρ)满足(RCP1)和(RCP2)即可．设a∈S，∀a′∈W(a),由ρ是S上的正则同余，则存在a″∈W(a)，使得aρaa″a，因此aa′ρaa″aa′，a′aρa′aa″a，其中aa′,a′a,aa″aa′,a′aa″a∈，则aa′htrρaa″

aa′,a′ahtrρa′aa″a．从而满足RCP1．设∀a∈S,x∈，xa∈K,则(xa)ρ∈E(S/ρ)．又因ρ是S的正则同余，则存在a″∈W(a)使得aρaa″a，又aρaa″aρaa″(xa)a″a，由aa″a″a∈ρaa″a″a(E(S/ρ)是矩形带)，因此aρ=(aa″a″a)ρ∈E(S/ρ)，即a∈K，因此(htrρ,kerρ)是S上的矩形群同余对．

下证ρ=ρ(htrρ,kerρ)．设aρb,∀a′∈W(a)，故a′bρa′a，即a′b∈K．由a′∈W(aρ)=W(bρ)，则存在b′∈W(b)使得a′ρb，因此aa′htrρbb′,a′ahtrρb′b，其中aa′,a′a,b′b,bb′∈ES．同理对∀b′∈E(b)，则存在a′∈W(a)，使得b′a∈K,aa′htrρbb′,a′ahtrρb′b，即aρ(htrρ,kerρ)b，故ρ⊆ρ(htrρ,kerρ)．

反之，设aρ(htrρ,kerρ)b,a,b∈S，因ρ是S上的正则同余，则存在

a″∈W(a)，b″∈W(b),使得aρaa″a,bρbb″b，因而存在b′∈W(b)，使得

aa″htrρbb′,a″ahtrρb′b,a″b∈K．另一方面，存在a′∈W(a)，使得aa′htrρbb′,a′ahtrρb″b,b′a∈K，因而

aρ=(aa″a)ρ=(bb′a)ρ=(bb′ab′a)ρ=(aa″ab′a)ρ=(ab′a)ρ，和bρ=(bb″b)ρ=(aa′b)ρ=(aa′aa′b)ρ=(aa″bb″b)ρ=(aa″b)ρ，则aρb，即ρ⊇ρ(htrρ.kerρ)，因此ρ=ρ(htrρ.kerρ)．

最后综合命题1,2,3,4，即可证明定理1．

[1]Bogdanovic S.Semigroups with a system of Subsemigroups[M].Novi Sad:Novi Sad University press,1985.

[2]Edwards P M.Eventually regular semigroup,Bull[J].Austral,math.Soc.,1983,28：23-38.

[3]Edwards P M.Congruence and Greens relations on eventually regular semigroups[J].J Austral.Soc.,1987,43：64-69.

[4]Hanumantha R S.Group congruences on eventually regular semigroup[J].JAustral.Soc.,1988,45：320-325.

[5]Latorre D R.Group congruences on regular semigroup[J].Semigroup forum,1988,45：320-325.

[6]Howie J M.Fundamentals of semigroups theory[M].Oxford:Clarendon Press,1995.

[7]Weipoltshammer B.Certain congruences on E-inverse E-semigroups[J].semigroup forum,2002,65(3):233-248.

[8]Zheng H W.Group congruences on an E-inverse semigroup[J].Southest Asia Bull Math,1997,21(1):1-8.

(责任编辑:陈衍峰)

10.13877/j.cnki.cn22-1284.2016.08.016

2016-04-22

安徽省自然科学基金项目“GV-半群及其子系统格的理论和方法研究”(1308085QA12)

王宇,安徽寿县人,博士,硕士生导师,讲师.

O152.7

A

1008-7974(2016)04-0049-03