矩形横截面导体内衰减振荡电流脉冲的趋肤效应

2016-12-19陶定峰顾邦平

浙江大学学报（工学版） 2016年4期

潘龙, 陶定峰, 何闻, 顾邦平

(1. 浙江大学浙江省先进制造技术重点实验室,浙江杭州 310027;2. 浙江大学流体动力与机电系统国家重点实验室,浙江杭州 310027; 3. 国网浙江省电力公司电力科学研究院,浙江杭州310014)

潘龙1,2, 陶定峰3, 何闻1,2, 顾邦平1,2

为了优化设计导通电流脉冲的工件以及制定电流脉冲处理材料的工艺方案,研究电流脉冲通过时电流密度、电磁场等物理量在导体内部的分布情况.根据Maxwell方程组,推导出振荡衰减电流脉冲通过矩形截面金属导体时,电场强度、电流密度、磁感应强度、电磁能密度和Maxwell应力张量在横截面分布的解析解.以电容放电通过碳钢板状试样为例,计算相关物理量的分布情况.结果表明,电流、电磁场的分布存在明显的趋肤效应,表面处的数值远远大于心部,主要分布在距离表面深度不大于趋肤深度的表层区域.电场强度、电流密度、磁感应强度、电磁能密度和Maxwell应力张量都呈现出振荡衰减的变化趋势.通过电流脉冲对45碳钢横截面碳原子作用的不均匀现象验证了趋肤效应的存在.

振荡电流脉冲；趋肤效应；电磁场；电流密度；Maxwell应力张量

随着电流脉冲(ECP)技术以及材料处理工艺的不断发展,ECP作为一种新的材料处理工艺,能够改变材料的微观结构[1-5],改善材料的力学性能[6-9],在材料加工领域得到了广泛应用,例如用电流脉冲辅助金属工件切割[10-11]、拉丝[12]、滚轧[13]、调控残余应力[14-16]等.此外,在电流脉冲技术中,要设计合理的导体工件,用来接通电流脉冲发生装置和所要施加的设备.为了确定这些工件的导电效率和安全系数,需要研究ECP在导体内的分布情况.

研究ECP提高材料性能的工艺以及设计传导电流脉冲的工件,都需要研究ECP通过时的电流、电场、磁场等物理量的分布情况.在材料处理中,通常采用电容放电的方法产生高能振荡电流脉冲,改变材料性能或微观结构[4-6,8-9,16].电容产生的振荡衰减电流脉冲通过材料时发生趋肤效应,Troitskii等[17-18]在研究圆形截面金属导体的“电致塑性”现象中发现趋肤效应的存在,Molotskii等[19-20]研究了圆形截面电流分布的趋肤效应.在许多情况下,工件的横截面是矩形的,例如,宋辉[6]研究ECP对钛合金板材组织和性能的影响,Cai等[14]研究电流脉冲对残余应力影响时采用的板状试样.接通电流脉冲的导体工件通常采用矩形截面,便于接通紧固.对于矩形截面工件,求解较复杂,目前的研究文献较少,本文分析矩形横截面导体内衰减振荡电流脉冲通过时电流、电场、磁场、能量以及Maxwell应力张量的分布情况.

本文分析矩形截面金属导体的电磁趋肤效应,以矩形截面的45碳钢试样为例,计算出相关物理量的分布.通过电流脉冲对淬火45碳钢试样横截面碳原子偏聚的影响,验证趋肤效应的存在.

1 理论分析

ECP通常利用电容放电产生.根据ECP的基本回路,分析ECP的振荡衰减变化情况,并根据测量的通过金属工件的电流,拟合出ECP变化的表达式.根据Maxwell方程组以及本构关系,求解出电流脉冲密度、电场强度、磁感应强度、能量和Maxwell应力张量在工件横截面的分布函数.

1.1 电容放电回路分析

图1 电容放电电路和产生的脉冲电流Fig.1 Circuit of capacitor discharge and generated pulse current

采用高压电容器进行储能放电产生ECP.将电容放电回路等效成图1(a)所示的电路.图中,K为开关,C为电容,U0为电容器充电电压,R为放电回路的总电阻,L为放电回路的总电感,i为回路电流.如图1(a)所示为RLC二阶串联电路,根据基尔霍夫电压定律,得到电路方程如下：

(1)

式(1)对时间t微分,得到二阶常系数微分方程：

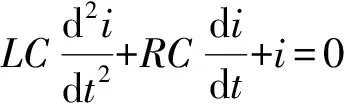
(2)

图1(a)中电路的初始条件为

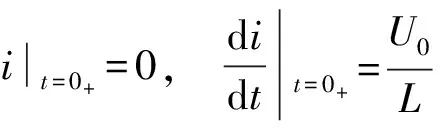
(3)

式(2)的特征方程为

LCr2+RCr+1=0.

(4)

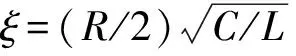
I(t)=I0exp (-δt)sin (ωt).

1.2 电磁场分析

利用ECP随时间变化的函数,进一步求解电流、电场、磁场等在横截面的分布情况.在金属导体中,Maxwell方程组为

(6)

式中：E为电场强度,B为磁感应强度,H为磁场强度,D为电位移,J为电流密度,ρv为自由电荷密度.上述变量之间的本构关系为

J=σE,D=εE,B=μH.

(7)

式中：σ为电导率,ε为介电常数,μ为磁导率.对于金属材料,·D=ρv=0,根据式(6)、(7)可得

(8)

(9)

进一步由式(8)、(9)推导出

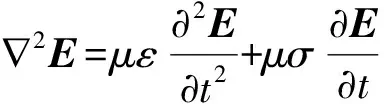
(10)

当电场随时间周期变化时,即E=E0exp (-jωt)i(i为x方向的单位法向量)，代入式(10),可得

2E=jωμ(jωε+σ)E.

(11)

为了简化方程,定义常数传播常数γ：

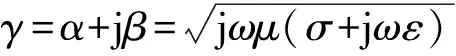
(12)

(13)

式中：α为空间衰减系数,反映了电场强度的幅值由表面到中心随厚度方向衰减的情况.幅值由表面到内部降低到1/e的厚度为趋肤深度：

(14)

对于金属材料,由于σ/(εω)≫1,式(13)简化为

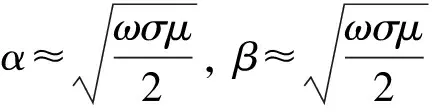
(15)

式(15)表明,ω、σ、μ越大,趋肤深度d越小,趋肤现象越明显.

将式(12)插入式(11),可得求解E的微分方程：

2E=γ2E.

(16)

对于矩形截面试样,当电磁场的传播方向为x轴时,如图2所示,边界条件[21]为

(17)

图2 试样横截面和边界条件Fig.2 Cross section and boundary conditions of samples

对于周期函数的稳态响应,电场幅值在横截面分布的情况[21]为

E(y,z)=

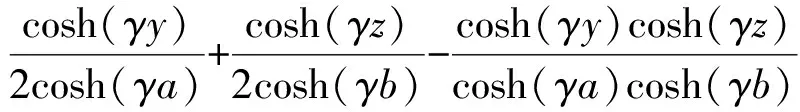
(18)

根据分离变量法可知,电场的解析解写为

E(y,z,t)=Ex(y,z,t)i=E0E(t)E(y,z)i.

(19)

式中：无量纲函数E(t)、E(y,z)分别反映了电场相对强度随时间和空间变化的情况.根据式(5)、(7)可得

E(t)=exp (-δt)cos(ωt+φE).

(20)

式中：φE为电场的初始相位,电流相位与电场相位相同,φE= 0.将式(18)、(20)代入式(19),可得电场在横截面的分布及随时间变化的情况：

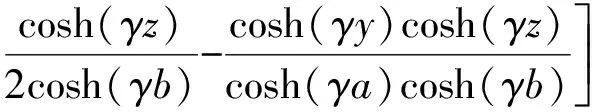
(21)

根据式(7),可得电流的解析解为

J(y,z,t)=σE(y,z,t).

(22)

在tm时刻,工件横截面上电流积分等于电流的最大值,即∬AJ(y,z)dA=Im,据此可以求出E0.

采用分离变量法,磁感应强度随空间和时间变化的解析解写为

B(y,z,t)=B0B(t)[By(y,z)j+Bz(y,z)k],

(23)

B(t)=e-δtcos(ωt+φB).

(24)

式中：B0为常量,φB为磁场的初始相位,并且

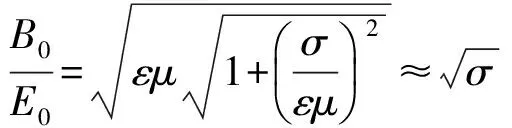
(25)

φB-φE=φ=arctan (α/β).

(26)

将式(18)～(20)、(23)、(24)代入式(6),求得

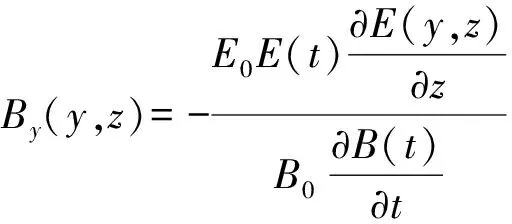
(27)

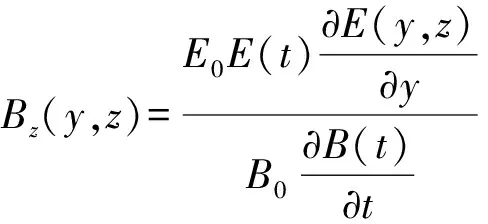
(28)

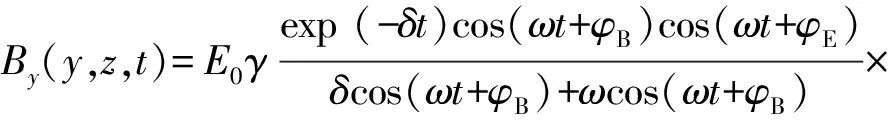
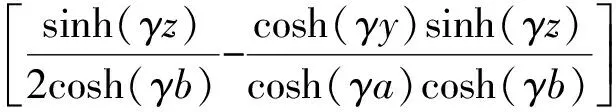
(29)

Bz(y,z,t)=

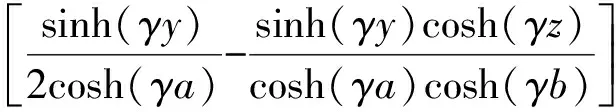
(30)

1.3 电磁场能量和Maxwell应力分析

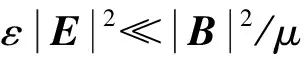
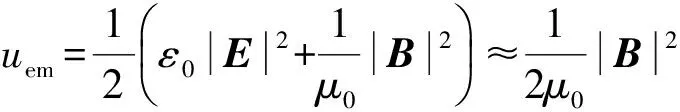
(31)

忽略电场对Maxwell应力张量的影响,并且磁感应强度计算结果表明,Bz(y,z,t)作用的部位很小,不考虑Bz(y,z,t)对Maxwell应力张量的影响.只计算By(y,z,t)产生的Maxwell应力张量,表达式为

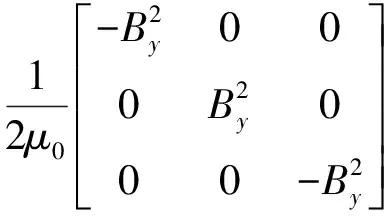
(32)

2 计算结果与分析

当图1(b)所示的ECP通过45钢矩形截面试样时,横截面尺寸为10 mm×1 mm,根据以上理论,计算相关物理量随空间和时间的变化情况.45钢的相关物理参数如下：电导率=107S/m[23],相对介电常数εr=1,相对磁导率μr=700[24].图1所示ECP振荡周期为T=1.62×10-4s,则ω=38 700 rad/s,根据式(14)计算出趋肤深度d=0.077 mm.

图3 电场强度Ex、电流密度Jx和磁感应强度By、Bz分布图Fig.3 Distribution map of electric field intensity Ex, current density Jx and magnetic flux density By, Bz

当t= 0.036 ms时,x轴方向的电场Ex、电流密度Jx达到最大值,Ex和Jx在横截面上的分布如图3(a)、(b)所示；当t=0时,磁感应强度达到最大值,y轴和z轴方向的磁感应强度By、Bz在横截面上的分布如图3所示.由图3(a)、(b)可以看出,Ex和Jx主要分布在试样的表面区域,心部较小,而且表面处的数值最大.图3(c)表明,By主要分布在试样的上、下表面,并且两个表面的磁感应强度方向相反,上表面磁感应强度为正值,下表面为负值.图3(d)表明,Bz集中分布于试样的棱边区域内,其他大部分区域很小.电场强度、电流密度和y轴方向的磁感应强度沿线段BA的分布情况,如图4所示.图4的结果表明,表面处电场强度、电流密度和磁感应强度远远大于心部区域,主要分布在深度不大于趋肤深度d的区域,心部大部分区域数值很小.

图4 电场强度Ex、电流密度Jx和感应强度By沿BA段分布情况Fig.4 Distributions of electric field intensity Ex, current density Jx and magnetic flux density Byalong BA line

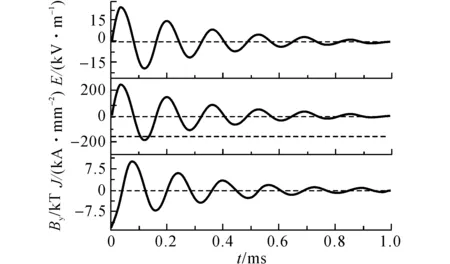
图5 点A处电场强度Ex、电流密度Jx和磁感应强度By随时间的变化Fig.5 Curves of electric field intensity Ex, current density Jx and magnetic flux density By versus time of point A

表面点A处的Ex、Jx和By随时间的变化如图5所示.Ex和Jx波形保持一致,不存在相位差,随着时间振荡衰减,在t=1 ms时,接近于0.By与Ex相比,磁感应强度最大时电场强度最小,磁感应强度最小时电场强度最大,存在90°相位差.磁感应强度随着时间的增加,振荡衰减,最后趋于0.

根据式(31)、(32)可知,磁感应强度By最大,即t= 0时,电磁能密度uem和Maxwell应力张量T11最大,在横截面的分布如图6(a)、(b)所示.由图6可以看出,电磁能和Maxwell应力T11主要分布在试样的上、下表面,T11为负值,表明为压应力.uem和T11沿线段BA的分布如图7所示,电磁能和Maxwell应力T11主要分布于距离表面深度小于趋肤深度d的区域,并且心部大部分区域数值很小,接近于0.电磁能密度uem和Maxwell应力张量T11随时间的变化如图8所示,呈现出振荡衰减的趋势,最后趋于0.

图6 电磁能密度和Maxwell应力张量的分布Fig.6 Distributions of electromagnetic energy density and Maxwell stress tensor

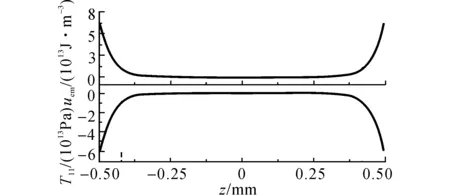
图7 电磁能密度uem和Maxwell应力张量T11 沿BA的分布Fig.7 Distributions of electromagnetic energy density uem and Maxwell stress tensor T11 along line BA

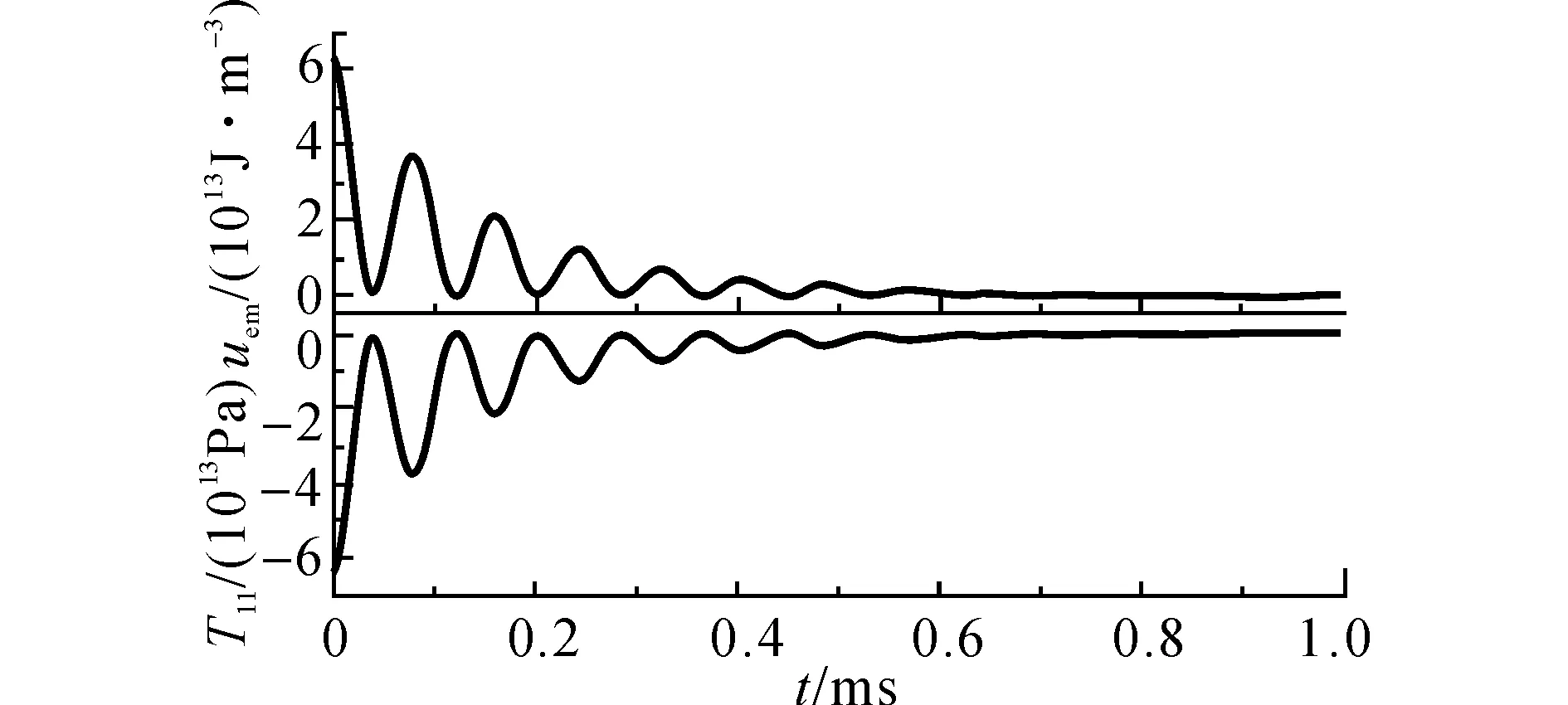
图8 点A处电磁量密度uem和Maxwell应力张量T11随时间的变化曲线Fig.8 Curves of electromagnetic energy density uem and Maxwell stress tensor T11 versus time of point A

根据Ex、Jx、By、uem和T11在试样横截面的分布情况,工件表层为这些物理量的主要分布区域,心部大部分区域在电流脉冲通过的过程中,几乎没有起到传导作用.在使用电流脉冲处理金属材料时,要充分考虑衰减振荡电流脉冲的趋肤效应.

3 实验验证

为了验证电流脉冲趋肤效应的存在,对上述45碳钢试样淬火后,采用图1(b)所示的电流脉冲,每4 s对试样施加一次,处理时间为40 min.对45碳钢试样淬火处理的目的是使碳原子以过饱和状态均匀地溶于铁素体内.淬火工艺如下：850 ℃下保温3 min,完全奥氏体化,室温下水淬.采用JEOL-JSM 6700扫描显微镜附带的电子探针能谱仪(EDS)分析横截面碳原子分布情况.在电流脉冲处理前、后,横截面沿oA线段不同深度a、b(z=0.05、0.45 mm)两处碳原子相对含量分布如图9所示.

由图9看出,刚淬火后的碳钢试样,碳原子在横截面均匀分布；在电流脉冲处理后,表面区域(z=0.05 mm)碳原子发生了较严重的偏聚现象,内部没有发生明显的偏聚现象.电流能够促进间隙碳原子的扩散[3,25],产生偏聚现象.实验结果表明,电流脉冲对试样表面处碳原子偏聚现象的作用明显大于心部,因此表面处的电流密度大于心部,表明趋肤效应的存在.

图9 电流脉冲对45碳钢淬火试样横截面碳原子分布的影响Fig.9 Effect of ECP on carbon distribution ofas-quenched 45 carbon steel specimens

分析导体横截面碳原子偏聚的不均匀程度与电流分布的关系.由图4看出,距离表面区深度为0.05 mma处的电流密度为1.32×1011J/m2,深度0.45 mm的b处电流密度分别为8.07×108J/m2,a处的电流密度远远大于b处.由图9可以看出,电流脉冲处理后,试样横截面碳原子在a处的偏聚现象远远大于b处,实验结果与电流分布情况一致,存在明显的不均匀现象.a处的深度小于趋肤深度(d=0.077 mm),验证了在小于趋肤深度的表层区域电流密度远大于心部区域.碳原子分布的实验结果验证了电流分布的计算结果,即存在明显的趋肤效应.在设计导通电流脉冲的工件以及采用电流脉冲处理材料时,要充分考虑衰减振荡电流脉冲的趋肤效应.

4 结论

(1) 给出振荡衰减电流脉冲通过矩形截面工件时,电场强度、电流密度、磁感应强度、电磁能密度和Maxwell应力张量随时间和空间变化的解析解.

(2) 电场强度、电流密度、电磁能密度和Maxwell应力张量主要分布在距离表面深度不大于趋肤深度d的表层区域,并且表面处数值远远大于心部；矩形截面工件的磁感应强度By主要分布在试样的上下表面,Bz集中分布于试样的棱边区域,物理量的分布存在明显的趋肤效应.

(3) 电流脉冲对淬火碳钢试样矩形横截面的碳原子的偏聚作用不同,对表面处碳原子偏聚的影响远大于心部,证实了振荡衰减电流脉冲趋肤效应的存在.

[1] STOLYAROV V V. Deformability and nanostructuring of TiNi shape-memory alloys during electroplastic rolling [J]. Materials Science and Engineering A, 2009, 503(1/2): 18-20.

[2] 关丽雅,郑秀华,王富耻,等. 电流密度对电铸铜晶粒组织的影响[J]. 稀有金属材料与工程，2009, 38(增1): 6. GUAN Li-ya, ZHENG Xiu-hua, WANG Fu-chi, et al. Influence of current density on grain structure of electroformed copper [J]. Rare Metal Materials and Engineering, 2009, 38(supple.1): 6.

[3] RAHNAMA A, QIN R S. The effect of electropulsing on the interlamellar spacing and mechanical properties of a hot-rolled 0.14% carbon steel [J]. Materials Science and Engineering A, 2015, 627: 145-152.

[4] XU X, ZHAO Y, MA B, et al. Rapid grain refinement of 2024 Al alloy through recrystallization induced by electropulsing [J]. Materials Science and Engineering A, 2014, 612: 223-226.

[5] XU X, ZHAO Y, MA B, et al. Rapid precipitation of T-phase in the 2024 aluminum alloy via cyclic electropulsing treatment [J]. Journal of Alloys and Compounds, 2014, 610: 506-510.

[6] 宋辉.电流脉冲处理对钛合金板材组织和性能影响的研究[D].哈尔滨：哈尔滨工业大学,2009. SONG Hui. Study on the effects of electropulsing on microstructures and properties of titanium alloys sheet [D]. Harbin: Harbin Institute of Technology, 2009.

[7] 张伟,隋曼龄,周亦胄,等.高密度电脉冲下材料微观结构的演变[J].金属学报,2003, 39(10): 1009-1018. ZHANG Wei, SUI Man-ling, ZHOU Yi-zhou, et al. Electropulsing-induced evolution of microstructures in materials [J]. Acta Metallurgica Sinica, 2003, 39(10): 1009-1018.

[8] LI X, ZHOU Q, ZHAO S, et al. Effect of pulse current on bending behavior of Ti6Al4V alloy [J]. Procedia Engineering, 2014, 81: 1799-1804.

[9] ZHU R F, LIU J N, TANG G Y, et al. The improved superelasticity of NiTi alloy via electropulsing treatment for minutes [J]. Journal of Alloys and Compounds. 2014, 584: 225-231.

[10] KUMAR P, MISHRA A, WATT T, et al. Electromagnetic jigsaw: metal-cutting by combining electromagnetic and mechanical forces [J]. Procedia CIRP, 2013, 6: 600-604.

[11] BARANOV S A, STASCHENKO V I, SUKHOV A V, et al. Electroplastic metal cutting [J]. RussianElectrical Engineering, 2011, 82(9): 477-479.

[12] TANG G, ZHANG J, YAN Y, et al. The engineering application of the electroplastic effect in the cold-drawing of stainless steel wire [J]. Journal of Materials Processing Technology, 2003, 137(1): 96-99.

[13] MAL′TSEV I M. Electroplastic rolling of metals with a high-density current [J]. Russian Journal of Non-Ferrous Metals, 2008, 49(3): 175-180.

[14] CAI Z, HUANG X. Residual stress reduction by combined treatment of pulsed magnetic field and pulsed current [J]. Materials Science and Engineering A, 2011, 528(19/20): 6287-6292.

[15] STEPANOV G V, BABUTSKII A I, MAMEEV I A, et al. Redistribution of residual welding stresses in pulsed electromagnetic treatment [J]. Strength of Materials, 2011, 43(3): 326-331.

[16] 郑建毅,何闻,施彦彬.电脉冲消除45钢淬火件的残余应力[J].浙江大学学报：工学版,2012(08): 1407-1411. ZHENG Jian-yi, HE Wen, SHI Yan-bin. Eliminating residual stress in 45 steel quenching specim ens by electrical pulse [J]. Journal of Zhejiang University: Engineering Science, 2012(08): 1407-1411.

[17] TROITSKII O A, MAISTRENKO L G. Electroplastic deformation in metals [J]. Soviet Materials Science, 1974, 8(6): 686-689.

[18] KLIMOV K M, NOVIKOV I I. The “electroplastic effect”[J]. Strength of Materials, 1984, 16(2): 270-276.

[19] MOLOTSKII M I. Theoretical basis for electro-and magnetoplasticity [J]. Materials Science and Engineering A, 2000, 287(2): 248-258.

[20] SUZUKI H, KANAOKA M. Theoretical investigation on skin effect factor of conductor in power cables [J]. Electrical Engineering in Japan, 2008, 156(1): 807-820.

[21] KOSEK M, TRUHLAR M, RICHTER A. Skin effect in massive conductors at technical frequencies [J]. Przeglad Elektrotechniczny, 2011, 87(5): 179-185.

[22] GRIFFITHS D J. Introduction to electrodynamics [M]. Beijing: Pearson Education Asia Limited, 2006: 345, 394.

[23] KAZUHIDE T A T W. An electrical resistivity study of lattice defects in deformed iron [J]. Japanese Journal of Applied Physics, 1972, 11(10): 1429-1439.

[24] http:∥zh.wikipedia.org/wiki/磁导率#cite_note-hyper-5[EB/OL].[2015-03-20].

[25] CONRAD H. Effects of electric current on solid state phase transformations in metals [J]. Materials Science and Engineering A, 2000, 287(2): 227-237.

Skin effect of decay oscillating current pulse in rectangular cross section conductor

PAN Long1,2, TAO Ding-feng3, HE Wen1,2, GU Bang-ping1,2

(1.ZhejiangProvinceKeyLaboratoryofAdvancedManufacturingTechnology,ZhejiangUniversity,Hangzhou310027,China;2.StateKeyLaboratoryofFluidPowerandMechatronicSystems,ZhejiangUniversity,Hangzhou310027,China;3.StateGridZhejiangElectricPowerCompanyPowerResearchInstitute,Hangzhou310014,China)

The distributions of current density, electromagnetic field and other physical parameters in the cross section when the pulse pass through the conductor were analyzed for the design of workpiece conducting current pulse and the process plan of treating materials by electric current pulse (ECP). The solutions for distributions of electric field intensity, current density, magnetic flux density, electromagnetic energy density and Maxwell stress tensor were deduced based on the Maxwell equations for the rectangular cross section conductor when ECP passed through it. The distributions of related physical parameters were calculated for carbon steel plate. Results show that a significant skin effect exists and the values of these parameters in the surface region are much larger than those in the internal region. Most of these parameters distribute in the region where the depth from surface is less than skin depth, and the physical parameters present an apparent decay oscillation varying with time. The skin effect of the decay oscillating current pulse in the rectangular cross section conductor was proved to be existed by the non-uniform distribution of carbon atom of the as-quenched 45 carbon steel specimens treated by ECP.

decay oscillating current pulse; skin effect; electromagnetic field; current density; Maxwell stress tensor

2015-03-26. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

航空科学基金资助项目(20140876003)；国家自然科学基金创新研究群体资助项目(51221004)；国家自然科学基金资助项目(50675200).

潘龙(1988—),男,博士生,从事残余应力调控技术的研究.ORCID: 0000-0002-8585-6574. E-mail: panlong0229@126.com 通信联系人,何闻,男,教授,博导.ORCID: 0000-0001-9089-3241. E-mail: hewens@zju.edu.cn

10.3785/j.issn.1008-973X.2016.04.005

O 442

1008-973X(2016)04-0625-06