泵控非对称液压缸系统高精度位置控制方法

王 玄, 陶建峰, 张峰榕, 吴亚瑾, 刘成良

(上海交通大学 机械与动力工程学院,上海 200240)



泵控非对称液压缸系统高精度位置控制方法

王 玄, 陶建峰, 张峰榕, 吴亚瑾, 刘成良

(上海交通大学 机械与动力工程学院,上海 200240)

针对已开发的单向比例泵控非对称液压缸系统实验平台,为了实现该类系统的无超调位置控制,通过分析系统的工作原理及特性,基于系统的流量连续性方程和力平衡方程,提出采用带约束的三阶状态空间模型来描述单向比例泵控非对称液压缸系统的方法.基于模型预测控制理论和QPhild二次优化算法,设计适用于该模型的模型预测控制器来保证系统的无超调位置输出.实验结果表明,运用模型预测方法能够避免换向阀切换引入的系统非线性,有效地解决泵控非对称液压缸系统的超调问题,实现多约束条件下的高精度位置控制.

泵控非对称液压缸；无超调；模型预测控制；位置精度控制；多约束

精密和节能是液压机产业的两大发展趋势.随着节能环保概念的日益普及以及下游产业对制品精度要求的不断提升,精密成形液压机正向高精度、低能耗方向发展.与闭式双向比例泵控系统相比,单向比例泵控非对称液压缸位置控制系统具有回路结构简单、无非对称缸流量平衡问题和不存在电机换向冲击等优点,在精密成形液压机上得到越来越多研究者的关注[1-7].

关于泵控非对称液压缸系统的液压回路和控制算法已经有了一定的研究[8-10],但其中关于单向变转速比例泵控非对称液压缸系统位置控制的相关理论及其在液压机上应用的文献非常少.目前,相对有参考价值的是关于双向比例泵控非对称液压缸的研究以及单向比例泵控非对称液压缸在注塑机上的相关应用.Perron等[11]采用滑模控制器对双向齿轮泵驱动的油缸进行位置控制,并与PI控制器的控制效果进行对比,位置控制精度不高,超调情况较严重.Zheng等[12]研究自整定模糊PID控制器在开关磁阻电机直接驱动液压机上的应用,通过仿真和试验分析PID参数对控制效果的影响.彭永刚等[13]研究单向比例泵控非对称液压缸系统在精密注塑中的应用,采用模糊滑模控制对系统的压力和速度进行控制.Peng等[14]在文献[13]的基础上,提出基于神经动态优化的模型预测控制器,对系统的进行速度控制,控制方法较新颖,但未对液压系统模型进行深入的研究.文献[11]、[12]都集中在位置控制的常规要求,例如快速性、稳定性、准确性和鲁棒性,实现无超调(产品出现尺寸负偏差的主要原因)、定位控制、精度控制等动态性能要求只能靠人工反复调试,调试成本较高、成功率较低.彭永刚等[13-14]着重对比例泵控非对称液压缸系统在注塑应用中的速度控制进行相关研究,相关结果无法直接应用于精密成型液压机.更重要的是,上述研究没有考虑到系统中存在的相关约束,包括：单向比例泵的转速必须在[0,nmax]内取值导致的输入约束,产品尺寸不能有负偏差导致的输出约束,系统工作压力不超过pmax导致的状态约束.

针对上述问题,本文采用带约束的三阶状态空间模型来描述单向比例泵控非对称液压缸系统.基于该模型提出适用于本系统的模型预测控制器,在为系统控制分析与综合提供理论与方法的同时,有效地实现了系统的无超调高精度位置控制.

1 系统描述

1.1 系统原理图

如图1所示为单向比例泵控非对称液压缸系统的原理图.系统由电机(1)、单项比例泵(2)、电磁换向阀(3)、非对称式液压缸(4)、油箱(5)、安全阀(6)、压力传感器(7,8)、控制器(9),位移传感器(10)、滑块(11)、弹簧(12)和阻尼(13)组成.

图1 泵控非对称液压缸系统原理图Fig.1 Schematic of pump-controlled asymmetric cylinder system

1.2 系统约束

1)泵为单向比例泵,泵的取值必须在内取值,即系统输入存在约束.

2)液压机的制品通常为不完全弹性体,在位置控制时如果超调存在,驱动模具的液压缸的最终位置与制品最终尺寸不对应(在控制作用下,液压缸最终能够到达指定位置,但如果有超调,不完全弹性的制品不能依靠弹性跟随液压缸回到相应尺寸),从保证制品尺寸的精度出发,希望系统输出无超调,即输出有约束.

2 系统建模

2.1 系统假设

关于图1,作如下假设.

1)油温和系统的油液体积弹性模量为常数.

2)泵为单向比例泵,且泵的转速与输入信号成正比.

3)系统压力没有沿程损失.

4)换向阀的压降很小,可以忽略不计.

5)由于活塞杆运动所引起的液压缸工作腔体积变化很小,可以忽略不计.

6)系统状态量的初值均为0.

7)液压系统中外泄相对较小,可以忽略不计.

8)系统在控制器作用下,系统接近目标位置过程中换向阀没有切换.

2.2 数学建模

依据系统假设,系统的液压回路简化成如图2所示的工作简图.

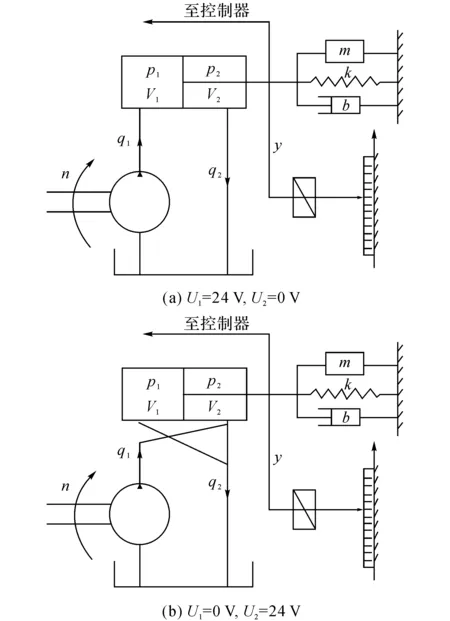
图2 泵控非对称液压缸工作简图Fig.2 Simplified hydraulic circuit for pump-controlled asymmetric cylinder

如图2(a)所示,当电磁换向阀的电压输出为U1=24 V,U2=0时,换向阀工作在左位,油液推动活塞向右运动,右工作腔的压力p2=0.此时,系统的流量连续性方程为

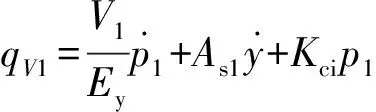
(1)

式中：V1为液压缸左工作腔的体积；Ey为体积弹性模量；p1为液压缸左工作腔的压力；As1为液压缸左工作腔的有效作用面积；Kci为内部泄露系数；qV1为此时泵的输出体积流量,可以表示为

qV1=Dpn.

(2)

式中：Dp为定量泵排量.如图2(b)所示,当电磁换向阀的电压输出为U1=0 ,U2=24 V时,换向阀工作在右位,油液推动活塞向左运动,左工作腔的压力p1=0.此时,系统的流量连续性方程为

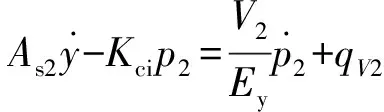
(3)

式中：V2为液压缸右工作腔的体积,p2为液压缸右工作腔的压力,As2为液压缸右工作腔的有效作用面积；qV2为此时泵的输出体积流量,可以表示为

qV2=-Dpn.

(4)

对液压缸活塞的受力情况进行分析,由牛顿第二定律可得

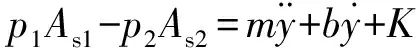
(5)

式中：m为滑块的质量,K为弹簧刚度,b为系统的阻尼,y为滑块的位移.考虑到系统的无超调需求,有

y≤r0.

(6)

式中：r0为系统的期望目标值.

由2.1节的假设2),有

(7)

考虑到泵的旋转单向性及最高转速nmax,有

0≤n=Knu≤nmax.

(8)式中：Kn为电机的输出输入比,u为系统的输入信号.

从式(1) ～(8)可以看出,当电磁换向阀处于不同的工作位置时,泵控非对称液压缸位置控制系统处于两种截然不同的工作状态,且系统中均存在输入和输出约束.若系统在工作过程中换向阀切换工作位置,该系统将变成一个高度的非线性系统,会给后续的位置控制带来十分的困难.若存在某种控制器,则能够使得系统在避免换向阀切换的前提下,在满足系统约束的条件下,无超调单向运动至期望的目标位置,达到期望的高精度位置控制要求,系统能够简化成一个带约束的线性控制系统.这将在很大程度上简化系统的模型,有效地缓解系统控制的难度.假设满足如上所述要求的控制器存在,根据式(1)、(3)、(5)～(8),泵控非对称液压缸位置控制系统可用如下的带约束的三阶状态空间模型来表示：

(9)

设系统状态变量：

X=[x1,x2,x3]T=[p1,y,y′]T,

控制变量U=u,输出变量Y=y, 由式(1) ～(7)可得

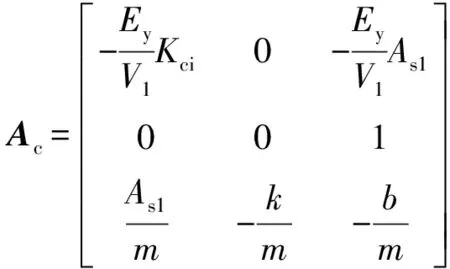
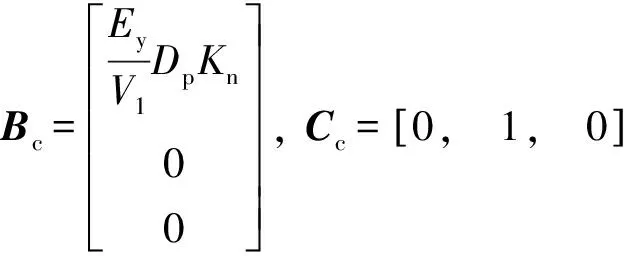
式中：Ac、Bc、Cc为连续系统的系数矩阵.

3 模型预测控制器的设计

该系统的特点是单向泵控液压缸系统控制输入只能在允许范围内,在系统压力允许的条件下,能够无超调地快速到达理想的目标位置.采用传统的控制方法无法处理系统过程中的输入、状态和输出约束,而模型预测控制 (model predictive control, MPC)作为新一代先进控制方法,可以很好地处理带有约束的优化问题.针对每一个控制时域的状态信息和约束条件,简化成相应条件下的二次规划问题,进行有限时域的滚动优化,从而使控制器在每一个时刻保持最优[15].

基于模型预测控制理论,首先对连续系统进行离散化处理[16],可得

(10)

式中：k为系统某采样时刻,Ad、Bd、Cd为Ts采样周期下的离散系统系数矩阵.

在状态空间模型中嵌入积分,可得增广模型:

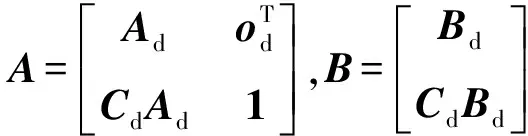
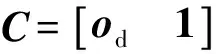
建立优化目标函数：

(11)

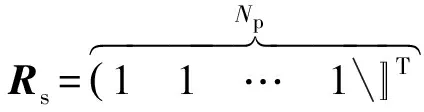
将目标函数和约束条件整理成二次规划方法标准形式：

(12)

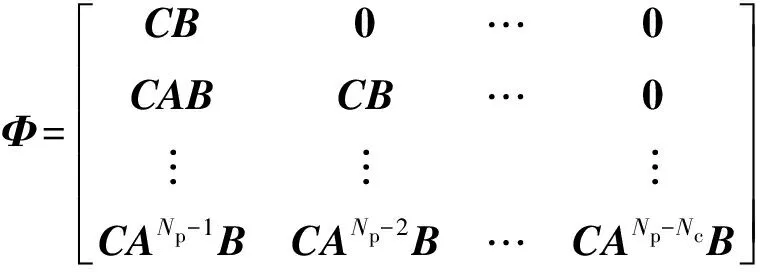
式中：M为系统的约束矩阵,η为约束向量,

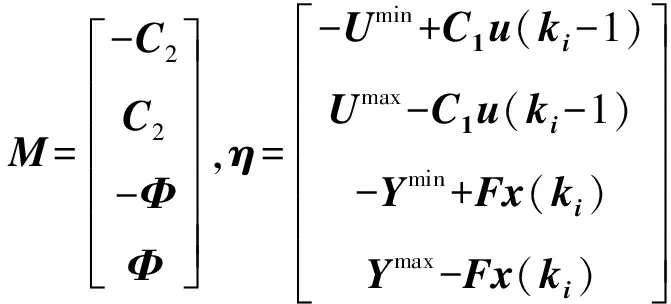
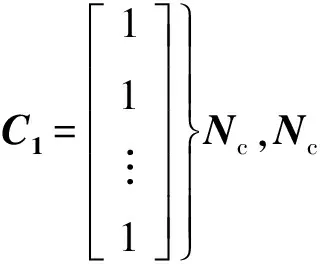
照社会主义的原则说，社会革命在资本制度发达到一定的程度的时候，自然要实现的，然而也可以用他种人为势力——非妥协的阶级斗争——促进他的速度。英、美的资本制度比俄国的要发达得十数倍，英、美两国的工会比俄国的也要发达得十数倍，何以社会革命不在英、美两国发生，反在俄国实现呢？这就是因为俄国社会革命党实行的力量比英、美两国的大的原故。所以我国在中国运动社会革命的人，不必专受理论上的拘束，要努力在实行上去做。

此时,原问题变成了求解带不等式约束的二次规划问题.假设系统每个采样时刻的状态变量X(k)已知,则可以通过二次优化算法QPhild算法[16]解出k时刻的最优输入序列：

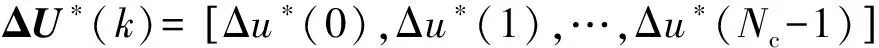
Δu*(k)=Δu*(0).

(13)

模型预测控制算法原理框图如图3所示.图3中,u(k-1)、u(k)分别为(k-1)时刻、k时刻的输入变量,x(k-1)、x(k)分别为(k-1)时刻、k时刻的状态变量,q-1为时间后移运算符.

模型预测控制算法原理图如图4所示.

考虑到实际液压系统中存在较多时变及不确定性因素,在预测控制算法中基于预测控制模型(不变)的预测输出不可能与系统的实际输出完全一致,而在滚动优化过程中,要求模型输出与实际系统输出保持一致.采用反馈校正,不断根据系统的实际输出对预测输出值作出修正,构成闭环反馈,具体做法如下.

将第k时刻的实际测量值与预测模型输出之间的误差附加到模型(k+1)时刻的预测输出ym(k+i)上,可以表示为

yp(k+i)=ym(k+i)+g0[(y(k)-ym(k)].

(14)

式中：yp(k+i)为k+i时刻的预测值,ym(k+i)为k+i时刻的模型预测输出值,y(k)为k时刻的实际测量值.

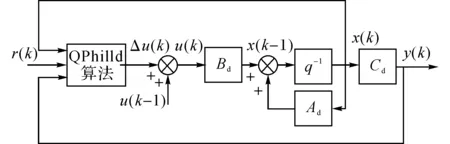
图3 模型预测控制算法原理框图Fig.3 Block diagram of control algorithm based on MPC

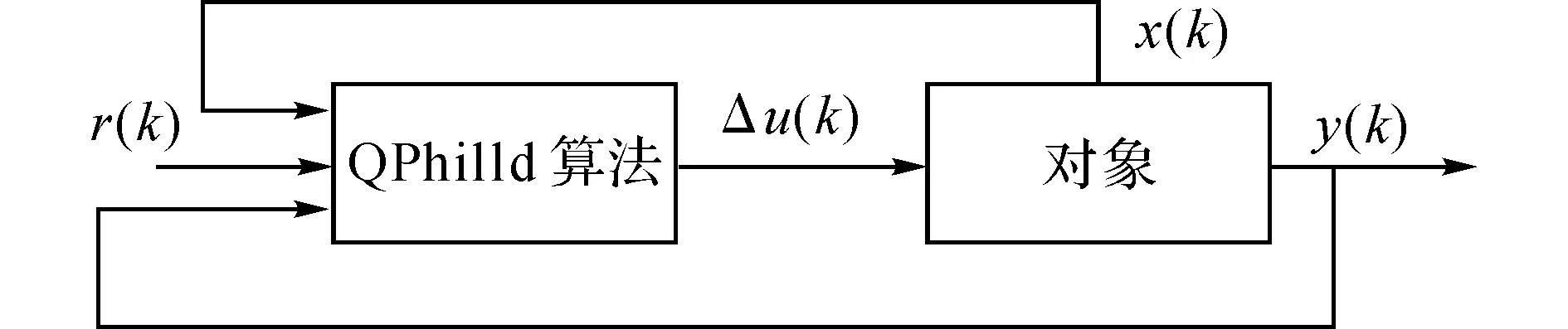
图4 模型预测控制算法原理图Fig.4 Schematic of MPC control algorithm

修正后的系统控制算法原理图如图5所示.

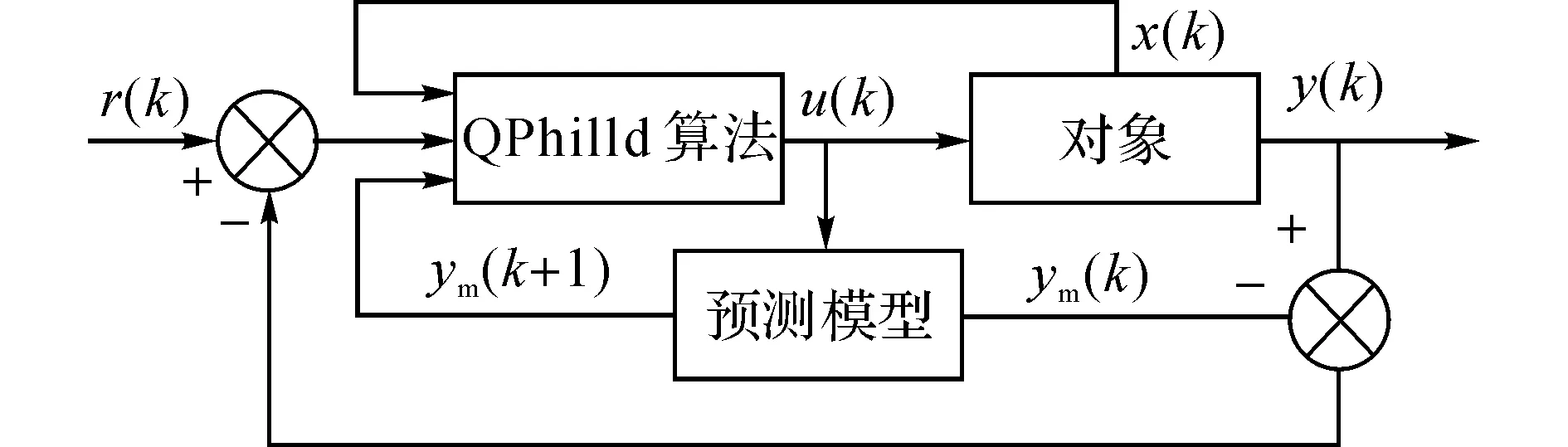
图5 修正后的模型预测控制算法原理图Fig.5 Modified schematic of MPC control algorithm

4 实验结果及分析

为了验证提出的控制器的实际控制效果,在实验室搭建泵控缸系统实验平台,如图6所示.电机选用三菱公司的HG-SR7024型交流永磁同步电机(搭配相应伺服器MR-J4-A)；压力传感器采用上海朝辉公司的PT124G-214型平膜式压力传感器；光栅尺选用信和公司的KA300-420型光栅尺；单向定量泵选用诚捷公司的NT3-D20F型内啮合齿轮泵.

实验平台的主要参数如表1所示,算法中所需的其他参数分别如下：Ey=1.4×109Pa,b=2 N/(m·s),Kci=2.4×10-13m3/Pa(由参数辨识获取).MPC控制器参数中,Np=30,Nc=3.基于上述参数,分别开展MPC与PID控制效果对比实验和不同目标值工况下的控制精度对比实验.

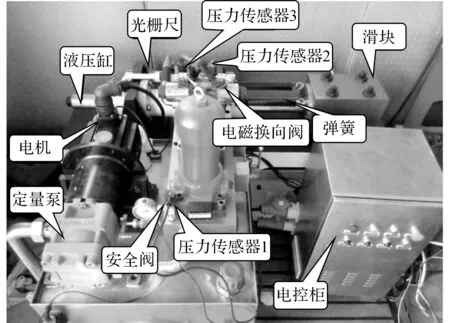
图6 泵控缸系统实验平台Fig.6 Test rig of pump-controlled cylinder system

4.1 MPC与PID控制效果对比

采用实验法试凑,选择一组无超调且控制效果相对较优的PID控制器参数Tp=700,Ti=0.002,Td=0.将实验结果与MPC实验结果进行对比,控制效果的对比如图7所示.可以看出,当选定合适的控制器参数时,MPC控制器和PID控制器系统均能够实现系统所需的无超调位置控制,但MPC控制效果在快速性方面远优于传统的PID控制.在实际调试中,PID参数的选择只能依靠试凑,具有较大的盲目性,系统调试效率很低；反之,MPC控制器参数在系统参数较明确的情况下,系统的无超调要求可以通过控制器结构来保证,参数的调整主要解决系统响应的快速性,调试过程无需花费太多时间.

表1 泵控缸系统试验台主要参数

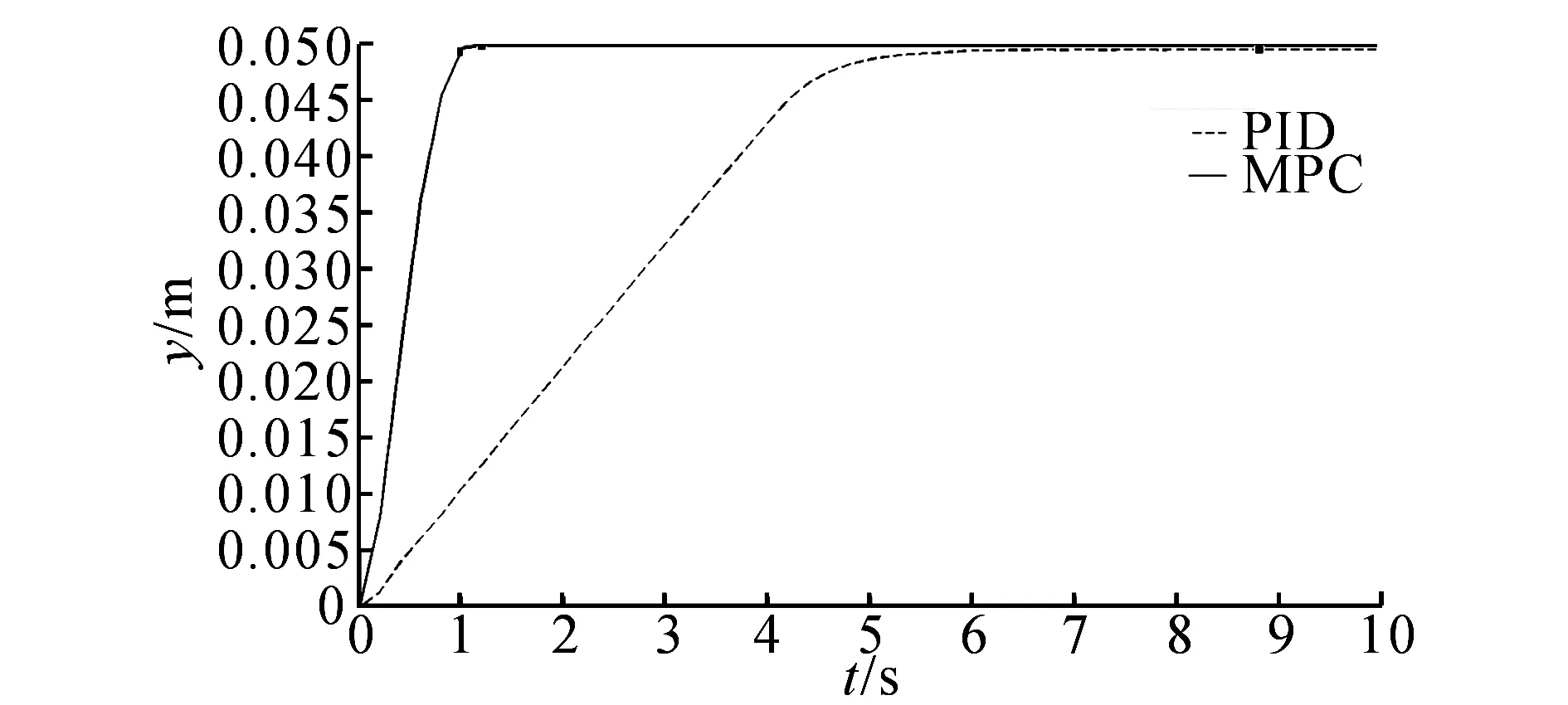
图7 MPC控制器与PID控制器控制效果对比图Fig.7 Control effect with proposed MPC and PID

4.2 不同目标值工况下的模型预测控制器效果对比

为了验证模型预测控制算法的控制精度,选择3种不同目标值工况进行试验：r0=0.05、0.07和0.10 mm.控制效果如图8所示.可以看出,在3种不同目标值工况下,系统均能够实现无超调输出,输出值误差Δy/y分别为0.53%、0.91%和0.18%,均能够控制在1%以内,控制精度良好.

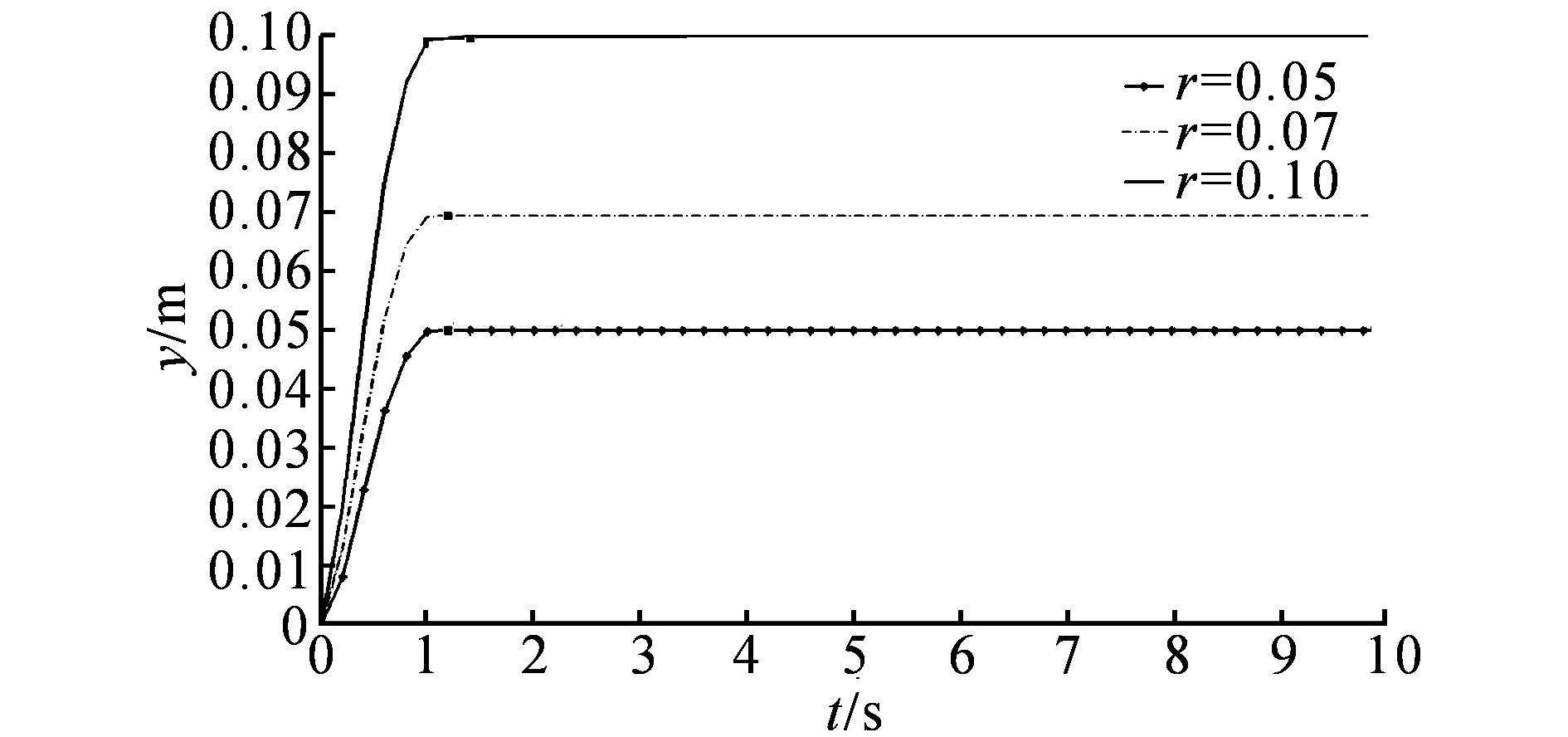
图8 不同目标值工况下的MPC控制效果图Fig.8 MPC control effect of different set-point

由实验过程及结果可知,模型预测控制器的控制效果优于传统的PID控制器,可以可靠地保证系统的输出始终满足y≤r0的要求；在系统工作过程中,y始终单调增大,因此,换向阀不用换向,有效地避免了换向时液压缸两工作腔压力突变造成的非线性影响.

5 结 语

本文针对单向比例泵控非对称液压缸位置控制系统,提出用带约束的三阶状态空间模型来描述本系统的简化模型.基于模型预测控制理论设计实用的模型预测控制器,通过实验进行验证.结果表明,相比于传统的控制方法,所设计的模型预测控制器能够将无超调约束、泵单向转动等条件转化成不等式约束条件下的二次规划问题,从而有效地避免阀切换导致的非线性因素对控制精度的影响,实现期望的无超调高精度位置控制.

[1] TAKAKU K, HIRAIDE H, OBA K. Application of the “ASR series” ac servo motor driven hydraulic pump to injection molding machines [C]∥Proceedings of the JFPS International Symposium on Fluid Power. Japan: The Japan Fluid Power System Society, 2008: 127-130.

[2] IMAMURA T, SAWADA Y, ICHIKAWA M, et al. Energy-saving hybrid hydraulic system comprising highly efficient IPM motor and inverter, for injection molding and manufacturing machine [C]∥Proceedings of the JFPS International Symposium on Fluid Power. Japan: The Japan Fluid Power System Society, 2008: 117-120.

[3] CHIANG M H. A novel pitch control system for a wind turbine driven by a variable-speed pump-controlledhydraulic servo system [J]. Mechatronics, 2011, 21(4): 753-761.

[4] RAHMFELD R. Development and control of energy saving hydraulic servo driven for mobile machine [D]. Hamburg: TUHH, 2002.

[5] HELDUSER S. Electric-hydrostatic drive: an innovative energy-saving power and motion control system [C]∥Proceedings of the Institution of Mechanical Engineers. Hangzhou: [s.n.], 1999: 427-437.

[6] KAZMEIER B. Electro-hydrostatic low power linear drive-system performance and controls to minimize power consumption [C]∥ Proceedings of the 3rd International Symposium on Fluid Power Transmission and Control. Beijing: International Academic, 1997: 113-119.

[7] XU M, JIN B, YU Y, et al. Using artificial neural networks for energy regulation based variable-speed electrohydraulic drive [J]. Chinese Journal of Mechanical Engineering, 2010, 23(3): 327-335.

[8] TAO J, WANG X, YANG L, et al. Nonovershooting position control for unidirectional proportional pump controlled asymmetric cylinder with proportional controller [C]∥ 2015 International Conference on Fluid Power and Mechatronics (FPM). China: IEEE, 2015: 866-872.

[9] 李贵闪. 伺服驱动液压机浅析[J]. 锻压装备与制造技术, 2011, 15(6): 17-19. LI Gui-shan. Analysis of servo-driven press [J]. China Metal Forming Equipment and Manufacturing Technology, 2011, 15(6): 17-19.

[10] 权龙. 泵控缸电液技术研究现状, 存在问题及创新解决方案[J]. 机械工程学报, 2008, 44(11): 87-92. QUAN Long. Current state, problem and the innovative solution of electro-hydraulic technology of pump controlled cylinder [J]. Journal of Mechanical Engineering, 2008, 44(11): 87-92.

[11] PERRON M, DE LAFONTAINE J, DESJARDINS Y. Sliding-mode control of a servomotor-pump in a position control application [C]∥ Canadian Conference on Electrical and Computer Engineering. Canada: IEEE, 2005: 1287-1291.

[12] ZHENG J, ZHAO S, WEI S. Application of self-tuning fuzzy PID controller for a SRM direct drive volume control hydraulic press [J]. Control Engineering Practice, 2009, 17(12): 1398-1404.

[13] 彭永刚,韦巍. 伺服电动机直接驱动定量泵液压系统在精密注塑中的应用及控制策略[J]. 机械工程学报,2011,47(2): 173-179. PENG Yong-gang, WEI Wei. Application and control strategy of servo motor driven constant pump hydraulic system in precision injection molding [J]. Journal of Mechanical Engineering, 2011, 47(2): 173-179.

[14] PENG Y, WANG J, WEI W. Model predictive control of servo motor driven constant pump hydraulic system in injection molding process based on neuro-dynamic optimization [J]. Journal of Zhejiang University: Science C, 2014, 15(2): 139-146.

[15] 黄昆, 俞凡. 电磁式主动悬架模型预测控制器设计[J]. 上海交通大学学报,2011, 44(11): 1619-1624. HUANG Kun, YU Fan. Model predictive controller design for electromagnetic active suspension [J]. Journal of Shanghai Jioatong University, 2011, 44 (11): 1619-1624.

[16] WANG L. Model predictive control system design and implementation using MATLAB [M]. Germany: Springer, 2009: 1-188.

Precision position control of pump-controlled asymmetric cylinder

WANG Xuan, TAO Jian-feng, ZHANG Feng-rong, WU Ya-jin, LIU Cheng-liang

(SchoolofMechanicalEngineering,ShanghaiJiaotongUniversity,Shanghai200240,China)

A three-order state space model with constraints was proposed to describe the system based on the flow continuity equation and the force balance equation after analyzing the operating principle and characteristics of the system in order to realize the non-overshooting position control of unidirectional proportional pump-controlled asymmetric cylinder system on the designed platform. A design of model predictive controller applicable to this model was proposed based on model predictive control theory and QPhild quadratic optimization algorithm in order to guarantee its non-overshooting output. Experimental results indicated that the proposed method successfully resolved the overshooting problem without introducing nonlinear characteristics caused by switching the valve. Then the aim of high-precision position control under multiple constraints was realized.

pump-controlled asymmetric hydraulic cylinder; non-overshooting; model predictive control; precision position control; multiple constraints

2015-11-18. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

国家自然科学基金资助项目(51375297，51275288)；上海市优秀学术带头人计划资助项目(14XD1402000)；国家“863”高技术研究发展计划资助项目(2012AA041803)；长安大学高速公路施工机械陕西省重点实验室开放基金资助项目(2014G1502044).

王玄(1992—),男,硕士生,从事电液伺服控制的研究.ORCID: 0000-0002-0722-2234. E-mail: wxasqy123@163.com 通信联系人：陶建峰,男,副教授.ORCID: 0000-0001-6098-9779. E-mail: jftao@sjtu.edu.cn

10.3785/j.issn.1008-973X.2016.04.001

TH 137; TP 271

A

1008-973X(2016)04-0597-06