高速列车头型气动反设计方法
2016-12-19陈大伟姚拴宝刘韶庆郭迪龙
陈大伟, 姚拴宝, 刘韶庆, 郭迪龙
(1. 中车青岛四方机车车辆股份有限公司 国家高速动车组总成工程技术研究中心,山东 青岛 266111;2. 中国科学院力学研究所 流固耦合系统力学重点实验室, 北京 100190)
高速列车头型气动反设计方法
陈大伟1, 姚拴宝1, 刘韶庆1, 郭迪龙2
(1. 中车青岛四方机车车辆股份有限公司 国家高速动车组总成工程技术研究中心,山东 青岛 266111;2. 中国科学院力学研究所 流固耦合系统力学重点实验室, 北京 100190)
基于支持向量机响应面模型,发展高速列车头型有约束气动反设计方法.为了减少流场计算量,针对反设计指标和约束条件分别建立对应的响应面模型,通过粒子群优化算法寻找满足设计目标值和约束条件的反设计外形.为了验证该方法的有效性,以3辆编组真实外形高速列车的1∶8缩比外形为研究对象,将整车气动阻力系数和流线型部分容积作为设计指标,研究单目标无约束、有约束及多目标无约束反设计方法.结果表明:采用提出的反设计方法能够快速得到满足设计指标和约束条件的高速列车头型,很容易拓展为能够解决任意复杂几何外形的多目标、有约束气动反设计方法,有利于提高高速列车头型工程设计的效率及针对性.
反设计; 支持向量机模型(SVR); 多目标设计; 高速列车
高速列车头部外形对列车气动性能的影响很大,通过改变头型可以有效地改善列车的气动性能[1-5],因此,头型设计是高速列车研制与发展的关键技术之一.头型设计的本质是设计合理的几何外形,气动设计方法主要有优化设计方法和反设计方法.近些年,高速列车头型的优化设计研究取得了很大进展[6-11],已有较成熟的优化方法和优化思路能够应用于工程实际问题[12],并取得了良好的成果.在头型设计过程中,更关注的是头型的综合气动性能,因此,很多情况下不追求头型某一气动指标的最优,而是希望得到满足某一给定气动力的头型,头型的反设计研究可以很好地达到这一目的.国内外很少见到关于高速列车头型的反设计方法研究,很有必要系统地研究该方法,并将其应用于工程实际问题,从而提高头型设计的高效性和针对性.
反设计方法主要用于解决翼型设计问题,虽然现在的反设计方法种类很多,但真正在工程上得到应用的方法基本上是以全位势方程为控制方法的反设计方法.常用的反设计方法主要有逆解法、虚拟气动法、余量修正法等.虽然这些方法在翼型设计领域都有成功的应用,但基本都是基于小扰动理论,当驻点高压区面积很大时,小扰动理论不再满足,这些方法失效.近几年,基于响应面技术的气动反设计方法[13]发展很快,且随着响应面技术的成熟,该方法逐渐应用于工程实际问题.该反设计方法的基本思路为:首先针对研究对象的外形进行参数化设计,提取控制外形的设计参数,根据各设计参数对应的几何约束条件确定其取值范围;然后在设计空间内通过采样方法获取训练样本点,根据得到的训练样本点,进行流场计算,得到各样本点对应的气动指标;基于训练样本点构建响应面模型,得到设计参数与设计指标的非线性函数关系;最后,通过优化算法搜索与给定的气动指标值一致的设计参数的值.该方法不存在任何假设,能够应用于任何复杂曲面及压力分布的反设计问题.
由于高速列车鼻锥区域存在强度很大的高压区,基于小扰动理论的反设计方法不再适用,而基于响应面技术的反设计方法能够很好的解决该问题.响应面的选取和构建是这种反设计方法的关键问题,目前,发展较为成熟的响应面技术有很多种,如二次响应面模型、Kriging模型、神经网络模型、支持向量机回归模型[14](support vector regression, SVR)等,对于不同的反设计问题,模型的选取也各不相同,SVR模型是发展较快的一种模型,能够较好的解决设计维数较高、计算量大的设计问题.本文在进行高速列车头型参数化设计时,需要确定的关键设计参数为30个,流场计算量很大,为提高头型反设计的效率,本文将基于SVR模型和粒子群优化算法,开展高速列车头型的无约束及有约束气动反设计方法研究.
1 几何外形及计算精度验证
高速列车头型的参数化设计是头型反设计方法研究的基础,为了较好地描述列车头型的几何外形,通过有限的设计参数控制头型曲面形状的变化,引入Rho等[15]提出的VMF参数化方法,具体的实现方法可以参考文献[16],本文不再赘述.由于排障器的曲面外形变化很大,为了精确地描述这种曲面,使用NURBS方法.对于头型的参数化设计,通过30个参数能够很好地控制列车头型的几何形状.简化外形虽然能够反映出列车周围流场的特性,但仍与真实外形存在较大的差别,为更好的将本文提出的反设计方法应用于工程实际问题,本文使用的列车外形为三辆编组真实外形的1∶8缩比外形,考虑风挡和转向架,在进行气动反设计时仅改变流线型部分(图1中的鼻锥和尾锥)的外形,列车几何外形如图1所示.
所有的气动设计指标均通过数值模拟方法得到,流线型部分的容积通过编制的FORTRAN程序计算得到.对于列车周围流场的数值计算,采用风洞试验环境,不考虑侧偏角,来流速度为60 m/s,空气的压缩效应对计算结果的影响不大.流场计算采用压力耦合方程组的半隐式方法(SIMPLE算法),湍流模型采用k-ωSST模型,车体壁面处使用标准壁面函数.地面为静止壁面,进口为速度入口边界,出口为压力出口边界,远场为滑移壁面.空间网格为正交六面体网格,车体表面布置三棱柱边界层网格,整体网格量为3 500万,空间及车体局部网格划分如图2所示.

图1 高速列车的几何外型Fig.1 Geometry of high-speed train
通过某型高速列车的风洞试验结果验证网格布置的合理性及数值计算方法的正确性.表1给出CFD计算结果与风洞试验数据.表中,TCd为整车气动阻力系数,HCd为头车气动阻力系数,MCd为中间车气动阻力系数,TaCd为尾车气动阻力系数,e为误差.试验数据以整车气动阻力系数为基础进行单位化处理.可以看出,中间车的气动阻力系数最小,计算误差最大,为6.37%,其他两节车厢的计算误差都在3%以内;对于工程设计,通常要求计算误差在10%以内,因此,各节车气动力系数的计算误差均在可接受的范围内,表明本文的网格布置及计算方法合理可行.
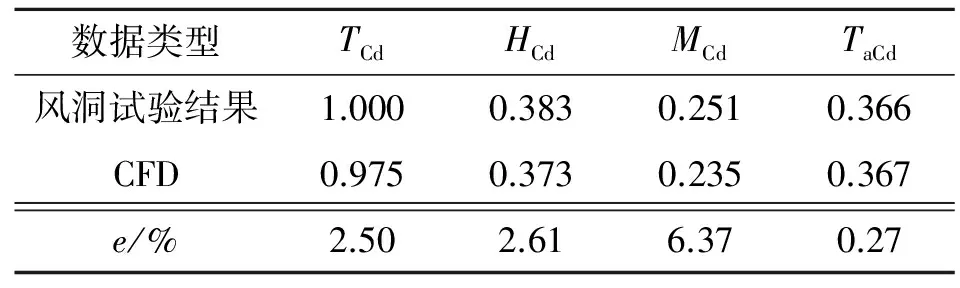
表1 高速列车的风洞试验结果与CFD计算结果

图2 计算域内的空间网格及车体表面网格Fig.2 Volume mesh in computation domain and surface mesh around high-speed train
2 SVR模型的构建
2.1 SVR模型
支持向量机(support vector machine,SVM)模型基于结构风险最小化原理,具有良好的推广能力、非线性处理能力和高维处理能力.对于非线性回归问题,SVM首先使用一个非线性映射将数据映射到一个高维特征空间,然后在高维特征空间进行线性回归,从而取得在原空间非线性回归的效果.为了解决在低维输入空间向高维特征空间的映射过程中空间维数的急剧增长而难以直接在特征空间计算最优超平面的问题,SVM引入核函数,将该问题转化到输入空间进行计算.SVM的回归算法有很多种,使用Shao等[17]提出的ε-TSVR(ε-twin support vector regression,ε-TSVR).ε-TSVR模型的基本理论可以参考文献[17],本文不再赘述,模型中的自由参数需要在构建过程中确定.为了减少训练样本点的数量,基于交叉验证算法和PSO优化算法构建ε-TSVR模型.
ε-TSVR模型的构建方法如下.
1) 交叉验证的初始化.对于给定的训练样本点集,根据具体情况确定样本集需要分成的组数l,然后对各训练样本点进行随机分组,确保每组训练样本点的个数相同.
2) PSO算法的初始化.给定粒子群算法的初始参数,如粒子群的数量、迭代步数等,粒子的数量和迭代步数对寻优效率的影响很大,不宜过大和过小.本文给定的粒子群数量为35,迭代步数为200.
3) 基于交叉验证思想的适应度函数.依次选取一组训练样本点作为检验样本点,使用其他训练样本点构建子SVR模型,得到检验样本点的预测误差RMSEi.利用下式计算PSO算法的适应度函数:

(1)
式中:l为训练样本点的组数;RMSEi为第i组检验样本点的预测误差,
(2)
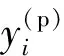
4) 使用PSO算法在给定的取值空间内寻优,得到自由参数的最优值.当使用SVR预测目标值时,以各个子SVR模型预测值的平均值作为最终的预测值.
2.2 以整车气动阻力为设计指标的SVR模型的构建
基于初始样本集构建的SVR模型的预测精度难以达到要求,此时需要引入多点加点准则,添加合适的训练样本点以提高模型精度.为了更加均匀地在设计空间内加点,采用的加点思路如图3所示.首先基于初始样本点集构建SVR模型,给定6个可能的设计指标值;然后基于SVR模型,通过PSO算法得到各设计指标值对应的设计变量值;接着使用参数化方法得到对应的高速列车头型,使用CFD方法得到各个头型对应的设计指标值,得到计算值与给定的设计指标值之间的误差.若误差满足工程设计要求,则SVR模型构建完成;否则,将6个设计点加入初始训练样本集,重新训练SVR模型,直到预测误差满足设计要求为止.
考虑的头型设计指标是3辆编组外形的整车气动阻力系数、流线型部分容积Vol.根据这两个设计指标,需要构建两套SVR模型.对于工程实际问题,气动力系数的预测误差在5%以内时,能够满足设计要求.为了尽量减少计算量,在构建SVR模型时,要求对各设计指标的平均预测误差在5%以内,允许设计空间内个别点的预测误差大于5%,但要小于10%.

图3 基于反设计方法的SVR模型构建思路Fig.3 Idea for construction of SVR based on inverse design
图4给出以整车气动阻力系数为设计指标时迭代加点过程中SVR模型的预测误差.图中,It为迭代次数.可以看出,随着加点次数的增大,即训练样本点数量的增加,设计点的预测误差逐渐减小,测试样本点的预测误差振荡减小,而整个设计空间内的平均预测误差保持在5%以内.经过5次加点,设计点和测试样本点的平均误差均小于5%,达到了设计要求,此时训练样本点的总个数为96.
表2给出以整车气动阻力系数为设计指标时,每次加点的目标值与各反设计外形的CFD计算值的误差.可以看出,基于初始训练样本集构建的SVR模型对测试点6的预测误差达到23.06%.随着训练样本点数量的增加,SVR模型对各反设计外型的预测误差逐渐减小.经过5次加点之后,反设计外型的平均预测误差小于5%,最大设计误差为6.13%,满足设计要求.可以使用构建完成的SVR模型开展以整车气动阻力系数为设计指标的头型反设计研究.
图5给出加点过程中的反设计外形,各外形与表2的设计点对应.可以看出,每次加点对应的反设计外形差别较大,随着流线型部分的容积不断增大,水平剖面型线在鼻锥尖端处的曲率变化越来越大,导致鼻锥钝度越来越大,整车气动阻力系数相应地逐渐增大.当整车气动阻力系数较小时,鼻锥以尖锥型为主,排障器外形多为后倾型;当整车气动阻力系数较大时,鼻锥以扁宽型为主,排障器外形多为前倾型.

图4 迭代加点过程中SVR模型的预测误差Fig.4 Prediction error of SVR during adding points

图5 加点过程中的反设计外形Fig.5 Inverse shape of added points
2.3 以流线型部分容积为设计指标的SVR模型的构建
在高速列车头型设计的过程中,为了保证车体内部设备的顺利安装及司机室足够的操作空间,需要严格控制流线型部分的容积.在开展头型反设计研究时,将流线型部分的容积作为一个设计指标.通过SVR模型拟合设计参数与流线型部分容积的非线性关系,SVR模型的构建方法与以整车气动阻力为设计指标时的构建方法相同.
图6给出根据初始训练样本点集.基于交叉验证算法和PSO优化算法构建SVR模型时的适应度f1收敛曲线.从图6可以看出,经过200代的搜索,适应度函数值趋于定值,即设计空间内的平均预测误差趋于定值.此时,平均预测误差仅为1.86%,满足工程设计的要求.
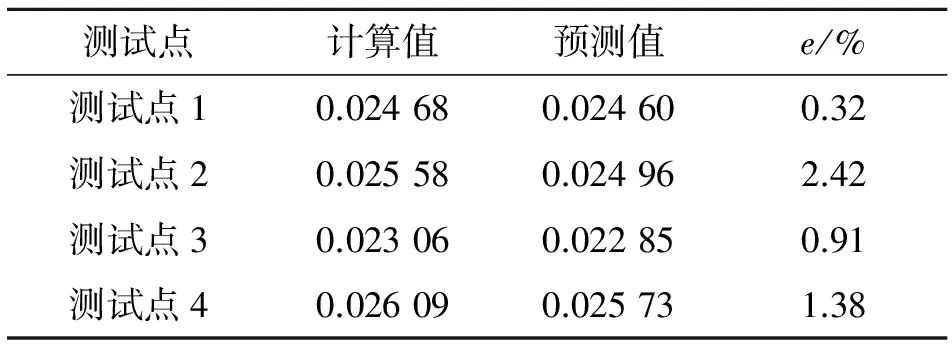
在进行头型的参数化设计时,将头型的长度进行单位化处理.给出的所有流线型部分容积的值均是单位化后的值,真实容积的值须扩大3 456倍,为了表述方便,本文不再给出容积的单位.表3给出以流线型部分容积为设计指标时的测试样本点的预测误差.可以看出,对于4个测试样本点,测试点2的预测误差最大,为2.42%;测试点1最小,仅为0.32%.各测试样本点的预测误差均满足设计要求,进一步验证了SVR模型的预测精度.

表2 各次所添加点的设计指标的给定值与反设计外形的计算值

图6 基于交叉验证算法构建SVR模型时的适应度收敛曲线Fig.6 History of fitness for construction of SVR based on cross-validation
表4给出设计指标的目标值与反设计外形的计算值.可以看出,6个反设计外形的流线型部分容积与对应的设计指标值的最大误差为4.55%,最小误差为1.26%,满足工程设计要求.通过上面的分析可知,以流线型部分容积为设计指标,基于初始训练样本点集构建的SVR模型的预测精度能够满足设计要求.
图7给出与表4各方案对应的反设计外形.对于相同的设计指标的目标值,可能对应多个反设计外形.在不影响SVR模型构建精度的情况下,针对每个目标值仅随机选取一个反设计外形.对流线型部分容积影响最大的因素是纵剖面型线和水平剖面型线在鼻锥尖端处的曲率,排障器外形对设备仓区域的容积影响较大.从图7可以看出,随着流线型部分容积的增大,鼻锥处的宽度和厚度逐渐增加,方案1接近于尖锥型,方案6接近于钝锥型.
表3 以流线型部分容积为设计指标时的测试样本点的预测误差
Tab.3 Prediction error of test points when taking volume as design target
测试点计算值预测值e/%测试点10.024680.024600.32测试点20.025580.024962.42测试点30.023060.022850.91测试点40.026090.025731.38

表4 设计指标的目标值与反设计外形的计算值

图7 反设计外形(与表4的各个方案对应)Fig.7 Inverse shape (corresponding to each case in Tab.4)
3 无约束反设计方法的实现
当设计参数的取值范围较大,即设计空间较大时,以设计参数为自变量、设计指标为因变量的函数通常为多峰值函数.若不施加约束条件,则在求解反问题时,往往会出现多解问题.此时,可以根据实际的工程需求选取合适的外形,也可以通过施加约束条件来减少解的数量.
基于构建的SVR模型,可以快速得到各设计参数与设计指标的隐式函数表达式.给定设计指标后,通过求解该表达式能够得到给定设计指标对应的设计参数值,由于无法得到显式函数表达式,难以通过传统方法求解方程,采用PSO算法在设计空间内寻找满足要求的解.当不考虑约束条件时,PSO算法的适应度函数为
f2=|cpd-ctg|.
(3)
式中:cpd为SVR的预测值,ctg为设计指标的目标值.
函数表达式为多峰值问题,在没有约束或约束很弱的情况下,满足同一个设计指标值的设计参数的值可能不止一组,因此对于同一个设计指标值,得到的高速列车头型也可能不止一个.
图8给出以整车气动阻力为设计指标,且设计指标的值为0.3时得到的3个反设计外形.可以看出,当设计指标的值相同时,得到的高速列车头型明显不同.这表明无约束条件时的反设计存在较多的解,针对工程实际问题设计头型时,应根据具体的需要选取合理的解.设计方案1和设计方案3的鼻锥存在显著的曲率不连续区域,且设计方案1的鼻锥宽度更大,设计方案2的鼻锥钝度很大,且排障器为一个尖锥.3个头型的整车气动阻力的最大差别仅为3.2%,与设计指标值的最大误差为3.13%,满足工程设计要求,验证了构建的SVR模型的有效性.
表5给出与图8对应的反设计外形的各节车厢的气动阻力系数和流线型部分容积.可以看出,虽然3个外形的整车气动阻力系数基本一致,但各车厢的气动阻力系数差别较大.设计方案1的头车气动阻力系数最小,但尾车气动阻力系数最大;设计方案3的头车气动阻力系数最大,但尾车气动阻力系数最小;设计方案2的头、尾车气动阻力系数处于中等水平,但中间车的气动阻力系数最大.在3个反设计外形中,设计方案2的流线型部分容积最大,在满足气动设计指标的前提下,头型的流线型部分容积越大越好,这样能够增大司机室空间,便于安置设备和提高操作舒适性.为了符合工程实际要求的反设计方法应添加必要的约束条件,从而过滤掉不满足设计要求的头型,减少头型设计的盲目性.
图9给出以流线型部分容积为设计指标,且目标值为0.03时得到的3个反设计外形.与目标值相比,设计方案1的误差最大,为4.83%;设计方案3的误差最小,为3%,均满足设计要求,3个头型的鼻锥钝度都很大,且都为扁宽型鼻锥.可见,鼻锥纵剖面型线和水平剖面型线的曲率对流线型部分的容积影响很大;设计方案1的鼻锥引流槽较深,设计方案2和设计方案3的鼻锥引流槽很浅,表明引流槽的设计方式对流线型部分容积的影响不是很大,具体的设计方式应根据头型的气动特性来确定.
表5 当TCd=0.3时各反设计外形的气动阻力系数及流线型部分容积
Tab.5 Drag force coefficient and volume of each inverse shape forTCd=0.3

设计方案HCdMCdTaCdVol设计方案10.08220.08250.14060.0266设计方案20.09080.08740.13120.0280设计方案30.09330.07730.12890.0266
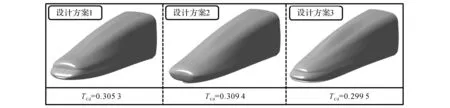
图8 同一设计指标值时的不同反设计外形(TCd=0.3)Fig.8 Different design shapes for same design target(TCd=0.3)

图9 同一设计指标值时的不同反设计外形(Vol=0.03)Fig.9 Different design shapes for same design target (Vol=0.03)
4 有约束反设计方法的实现
在高速列车头型的工程实际设计过程中,需要考虑的约束条件很多,头型不仅要满足安置设备和司机室操作所必须的空间,而且要满足一些重要的气动设计指标.有约束的反设计方法是需要解决的关键问题之一.
对于给定的设计空间,约束添加的是否合理直接影响到反设计的解是否合理,过强的约束条件容易导致反设计求解的失败.在解决工程实际问题时,应在满足实际需求的情况下尽量减弱约束条件,以便于找到更多合理的解.
当考虑约束条件时,PSO算法的目标函数应重新定义,考虑的约束条件主要为设计指标的限值,几何变量的约束条件主要通过设计变量的取值范围进行限定.通过添加惩罚函数项来反映约束条件对目标值的影响,考虑约束条件时的目标函数为
f3=|cpd0-ctg0|+wi|cpdi-ctgi|.
(4)
式中:cpd0为SVR模型预测的目标值;ctg0为给定的目标值;cpdi为约束条件的预测值;ctgi为约束条件的限值;wi为惩罚因子,对于不同的设计指标,可以选取不同的值,当wi=0时,式(4)退化为不加约束条件的适应度函数.
为了验证提出的高速列车头型有约束反设计方法的有效性,针对2个不同的设计指标进行分析.
首先以整车气动阻力系数为设计指标,流线型部分容积为约束条件进行头型反设计.图10给出整车气动阻力的目标值为0.3,流线型部分容积不小于0.027时得到的3个反设计外形.可以看出,与给定的目标值相比,设计方案2的预测误差最大,为8.23%;设计方案1的预测误差最小,为1.33%.由于本文以SVR模型在设计空间内的平均预测误差来判断模型的预测精度,难以保证设计空间内所有点的预测误差都小于5%,因此,设计方案2的预测误差大于5%是符合设计要求的.对于3个反设计外形,流线型部分容积最小的为设计方案1,容积为0.026 9,满足约束条件的要求.
表6给出与图10的反设计外型对应的各节车厢的气动阻力系数.可以看出,3个头型的头车气动阻力系数差别很大,设计方案1的头车气动阻力系数最小,设计方案2的头车气动阻力系数最大,两者相差12.63%;设计方案2的中间车气动阻力系数最大,设计方案3的中间车气动阻力系数最小,两者相差9.52%;设计方案2的尾车气动阻力系数最大,设计方案1的尾车气动阻力系数最小,两者相差14.32%.由于给定的列车运行速度仅为60 m/s,列车周围各部位流场的改变都会对其他部位的流场产生影响,头型的改变将会导致头、尾车附近的流场都发生变化[9-10,12],对中间车附近的流场产生影响,导致中间车气动阻力系数发生变化,在进行头型设计时不仅要考虑头型的变化对头、尾车气动性能的影响,而且要考虑对中间车气动性能的影响[12,18-19].

图10 整车气动阻力的目标值为0.3,流线型部分容积不小于0.027时得到的反设计外形Fig.10 Inverse shapes for TCd=0.3 and Vol≥0.027
表6TCd的目标值为0.3,Vol≥0.027时得到的反设计外形的气动力系数
Tab.6 Drag force coefficient of inverse shapes forTCd=0.3 andVol≥0.027

设计方案HCdMCdTaCd设计方案10.07920.08830.1285设计方案20.08920.08860.1469设计方案30.08450.08090.1452
对于不同的设计指标和约束条件,反设计得到的头型是不同的.图11给出以Vol为设计指标,且目标值为0.025 5,TCd为约束条件,且TCd≤0.28时得到的3个反设计外型.可以看出,各反设计外型的流线型部分容积的值与目标值基本一致,最大误差仅为0.78%,设计方案1和设计方案3的整车气动阻力系数都不满足约束条件,设计方案1的整车气动阻力系数比约束条件的上限值大2%,设计方案3的整车气动阻力系数比约束条件的上限值大3.93%,这主要是由SVR模型的预测精度引起的.给定的SVR模型在设计空间内的平均预测误差为5%,因此反设计外型的实际目标值和约束指标与给定的目标值和约束条件有所差别是允许的.若要减少这种差别,则应尽量提高SVR模型的预测精度,而这样会不断地增加流场计算次数,在针对工程实际问题进行头型反设计时,应充分考虑两方面因素,确定合理的预测误差.
表7给出与图11的反设计外型对应的各节车厢的气动阻力系数.可以看出,对于相同的流线型部分容积,头、中、尾车的气动阻力系数变化较大,尤其是尾车,绝对差的最大值达到0.008 1,头车的气动阻力系数变化幅度比中间车的气动阻力系数变化幅度大,表明头型的变化对头、尾车的气动阻力系数影响大于对中间车的气动阻力系数的影响,但是整列车处于亚声速流场之中,局部流场的改变对整个流场都会产生较大的影响.
表7Vol的目标值为0.025 5,TCd≤0.28时得到的反设计外形的气动力系数
Tab.7 Drag force coefficient of inverse shapes forVol=0.025 5 andTCd≤0.28

设计方案HCdMCdTaCd设计方案10.08120.08860.1158设计方案20.07870.08690.1125设计方案30.08470.08570.1206

图11 流线型部分容积为0.025 5,整车气动阻力系数不大于0.28时得到的反设计外形Fig.11 Inverse shapes for Vol=0.025 5 and TCd≤0.28
5 两目标无约束反设计方法的实现
高速列车的运行场景十分复杂,如明线运行、隧道内运行、列车交会等,在各个场景条件下,列车的头型对列车气动性能的影响都很大.在开展头型设计时需要考虑很多气动设计指标,仅对单个设计指标进行反设计得到的头型往往会导致其他气动设计指标变差,因此头型的单目标气动反设计方法难以满足工程实际设计要求,很有必要发展多目标气动反设计方法.
高速列车头型的关键设计参数与气动指标之间存在显著的非线性关系,开展头型的气动反设计方法研究,实质是求解复杂非线性方程或方程组.针对每个气动指标的反设计,即求解一个复杂的非线性方程,气动设计指标越多,需要求解的方程越多,问题越复杂.对于多目标气动反设计方法,要求各方程之间存在至少一个相同的解,在给定的求解域内,不能保证方程组有解;当加入严格的约束条件之后,方程组解的存在性更加难以确定.
为了确保多目标气动反设计方法的顺利实现,并得到满足要求的设计外形,首先给定合理的设计空间,在满足约束条件的前提下,须尽量增大每个设计参数的取值范围,以便于找到更多的解.当使用优化算法求解反设计问题时,目标函数的给定方式会影响反设计的结果.目前,应用较多的方法是给每个设计指标一个权重.权重越大,对应的设计指标的重要性越强,通过调整权值,能够很大程度地提高反设计结果的可行性.
基于PSO算法的多目标头型反设计方法,给定的目标函数为

(5)

对于两目标无约束反设计,设计指标为整车气动阻力系数和流线型部分容积,wi为0.5,即同等对待2个设计指标.图12给出当整车气动阻力系数为0.294,流线型部分容积为0.025 4时的2个反设计外形.这两个设计指标的值与初始外形的值相同,但得到的外形与初始外形有较大的不同,这主要是因为初始外形只是给定的设计条件中所有外形的一种特殊情况.若想根据设计条件得到初始外形,则须使用PSO算法在设计空间内进行若干次重复的寻优,直至得到所有满足条件的解,然后从中选取需要的外形.设计方案1和设计方案2的流线型部分容积和整车气动阻力系数与给定的设计指标的目标值基本一致,表明在设计空间内可以找到满足给定目标值的反设计外形.
通过上面的算例可以看出,采用提出的高速列车头型多目标无约束反设计方法能够较好地找到指定目标值的外形,为解决工程实际问题提供思路.

图12 TCd=0.294,Vol=0.025 4时对应的反设计外形Fig.12 Inverse shapes for TCd=0.294 and Vol=0.025 4
6 结 语
以3辆编组真实外形的风洞试验模型为研究对象,基于支持向量机响应面方法,完成了高速列车头型无约束及有约束的反设计方法,并提出多目标无约束反设计方法.通过算例验证,给定目标值后,使用本文方法能够快速得到满足目标值的反设计外形,表明采用提出的反设计方法能够较好地辅助解决高速列车头型的工程实际设计问题.
[1] RAGHUNATHAN R S, KIM H D, SETOGUCHI T. Aerodynamics of high-speed railway train [J]. Progress in Aerospace Sciences, 2002, 38(6): 469-514.
[2] YAO S B, SUN Z X, GUO D L, et al. Numerical study on wake characteristics of high-speed trains [J]. Acta Mechanica Sinica, 2013, 29(6): 811-822.
[3] BAKER C. The flow around high speed trains [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6/7): 277-298.
[4] 黄志祥,陈立,蒋科林.高速列车减小空气阻力措施的风洞试验研究[J].铁道学报, 2012, 34(4): 16-21. HUANG Zhi-xiang, CHEN Li, JIANG Ke-lin. Wind tunnel test of air-drag reduction schemes of high-speed trains [J]. Journal of the China Railway Society, 2012, 34(4): 16-21.
[5] YANG G W, GUO D L, YAO S B, et al. Aerodynamic design for China new high-speed trains [J]. Science China Technological Sciences, 2012, 55(7): 1923-1928.
[6] KRAJNOVIC S. Shape optimization of high-speed trains for improved aerodynamic performance [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223(5): 439-452.
[7] KU Y C, RHO J H, SU H W, et al. Optimal cross-sectional area distribution of a high-speed train nose to minimize the tunnel micro-pressure wave [J]. Structural and Multidisciplinary Optimization, 2010, 42(6):965-976.
[8] LEE J S, KIM J. Approximate optimization of high-speed train nose shape for reducing micropressure wave [J]. Industrial Applications, 2008, 35(1): 79-87.
[9] YAO S B, GUO D L, YANG G W. Three-dimensional optimization design of high-speed train nose based on GA-GRNN [J]. Science China Technological Sciences, 2012, 55(11): 3118-3130.
[10] KU Y C, KWAK M H, PARK H I, et al. Multi-objective optimization of high-speed train nose shape using the vehicle modeling function [C]∥48th AIAA Aerospace Sciences Meeting. Orlando: AIAA, 2010.
[11] VYTLA V V, HUANG P G, PENMETSAR C. Multi objective aerodynamic shape optimization of high speed train nose using adaptive surrogate model [C]∥28th AIAA Applied Aerodynamic Conference. Chicago: AIAA, 2010.
[12] YAO S B, GUO D L, SUN Z X, et al. Multi-objective optimization of the streamlined head of high-speed trains based on the Kriging model [J]. Science China Technological Sciences, 2012, 55(12): 3494-3508.
[13] 邓磊,乔志德,熊俊涛,等.多目标自然层流翼型反设计方法[J].航空学报, 2010, 31(7): 1373-1378. DENG Lei, QIAO Zhi-de, XIONG Jun-tao, et al. Multi-objective inverse design of natural laminar flow airfoils [J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1373-1378.
[14] VAPNIK V N. Statistical learning theory [M]. New York: Wiley, 1998.
[15] RHO J H, KU Y C, YUN S H, et al. Development of vehicle modeling function for 3-dimensional shape optimization [J]. Journal of Mechanical Design, 2009,131(12): 121004-1-10.
[16] YAO S B, GUO D L, SUN Z X, et al. A modified multi-objective sorting particle swarm optimization and its application to the design of the nose shape of a high-speed train [J]. Engineering Applications of Computational Fluid Mechanics, 2015, 9(1): 513-527.
[17] SHAO Y H, ZHANG C H, YANG Z M, et al. Anε-twin support vector machine for regression [J]. Neural Computing and Applications, 2013, 23(1): 175-185.
[18] YAO S B, GUO D L, SUN Z X, et al. Optimization design for aerodynamic elements of high speed trains [J]. Computers and Fluids, 2014, 95: 56-73.
[19] 陈大伟,姚拴宝,郭迪龙,等.高速列车头型拓扑结构对气动力的作用规律研究[J].铁道学报, 2015, 37(2): 18-26. CHEN Da-wei, YAO Shuan-bao, GUO Di-long, et al. Study of influence laws between topology structure of high-speed train head and aerodynamic force [J]. Journal of the China Railway Society, 2015, 37(2):18-26.
Inverse design for aerodynamic shape of high-speed train nose
CHEN Da-wei1, YAO Shuan-bao1, LIU Shao-qing1, GUO Di-long2
(1.NationalEngineeringResearchCenterforHigh-SpeedEMUEngineer,CRRCQingdaoSifangLimitedCompany,Qingdao266111,China; 2.LMFSofInstituteofMechanics,ChineseAcademyofSciences,Beijing100190,China)
A constrained inverse design method for the aerodynamic shape of high-speed train nose was developed based on the support vector regression (SVR) model. The SVRs for the design and constraint objectives were respectively established in order to reduce the CFD computation. Then the inverse design shapes that meet the target values and constraints could be found by the particle swarm optimization (PSO) algorithm. The scaled real shape (1∶8) for high-speed train with three carriages was taken as the study object in order to verify the inverse design method. The aerodynamic drag coefficient of the whole train and the volume of the streamlined part were taken as the design targets. The constrained and unconstrained single objective and multi-objective design method without constraints were analyzed. Results show that the proposed approach can quickly get the inverse shape that meets the design specifications and constraints. The approach can be easily expanded to solve constrained and multi-objective inverse problems for arbitrarily complex geometries. The approach may improve the engineering design efficiency of high-speed train nose.
inverse design; support vector regression (SVR); multi-objective design; high-speed train
2015-10-01. 浙江大学学报(工学版)网址: www.journals.zju.edu.cn/eng
“十二五”国家科技支撑计划资助项目(2013BAG24B02);国家“973”重点基础研究发展规划资助项目(2011CB711100);国家“863”高技术研究发展计划资助项目(2015AA01A302).
陈大伟(1982—),男,高级工程师,从事高速列车空气动力学和计算流体力学的研究.ORCID: 0000-0003-2333-6239. E-mail: chendawei@cqsf.com 通信联系人:姚拴宝,男,工程师.ORCID: 0000-0002-1341-1250.E-mail: ysbao566@163.com
10.3785/j.issn.1008-973X.2016.04.006
U 238
A
1008-973X(2016)04-0631-10
