基于多主体建模分析的银行间网络系统性风险研究

邓 超，陈学军，2

(1. 中南大学商学院，湖南 长沙 410083；2.中国人民银行郑州培训学院，河南 郑州 450011)



基于多主体建模分析的银行间网络系统性风险研究

邓 超1，陈学军1，2

(1. 中南大学商学院，湖南 长沙 410083；2.中国人民银行郑州培训学院，河南 郑州 450011)

本文基于多主体建模分析了银行间核心-边缘网络的系统性风险。模型假设银行通过最优投资组合配置，在流动性和资本约束前提下谋求利润最大化。通过建立银行间市场交易环境的仿真模型，依据银行行为决策动态形成资产负债表与银行间网络敞口的数据，评估金融监管政策在银行间市场的实施效应。同时，引入不同网络结构模型加以对比分析，发现尽管核心-边缘银行间网络体系比无标度网络更易遭受共同冲击和传染风险，但当处于金融困境时，在宏观审慎管理政策机制作用下，核心-边缘网络体系比其他结构网络表现出更强的恢复力特性。

多主体模型；银行间市场；系统性风险；核心-边缘网络；共同冲击

1 引言

在维护金融稳定的监管设计中，其主要目标是通过设计一系列适合的宏观审慎监管规则，加强金融体系的稳健性和恢复力。从理论上来讲，当银行间市场发生异质性的流动性冲击时，银行可以通过同业市场的互相拆借抵以御冲击的影响。如果非预期流动性需求出现，银行会从银行间市场借款，银行就处在筹集流动性资产过程。同时，银行间敞口也被看作银行彼此共同监督的有效交易指标。广义而言，银行间市场更主要的反映了银行之间存在的重要信用关系，借款银行之所以能够以较低的市场利率获得拆入资金，主要因为其与提供流动性贷款的银行之间有着紧密的关系，网络结构就较好地刻画了银行间这一关系。目前关于金融网络模型的研究大都沿袭Allen和Gale[1]对简单规则网络的研究思路，分别以ER随机网络、小世界网络和无标度(Scale-Free，SF)网络等典型拓扑结构描述银行体系的风险敞口关系。

关于银行间网络的分层结构模型的研究，仅在近几年才得以重视。Freixas等[2]较早地提出了以货币-中心为主导的银行分层体系易于遭受传染性风险。相比于ER随机网络结构的银行网络模型，银行网络分层特征对冲击更具有恢复力，即便是在危机情形下银行失败的频率也较ER随机网络低[3]。

Craig和von Peter[4]首先在银行间核心-边缘网络结构(Core-Periphery，CP)网络的量化方法上提出了严格的定义，一个纯粹的核心边缘结构必须满足以下两个条件：一是核心银行间必须彼此完全连接，并且至少与一个边缘银行存在拆入和拆借信用关系；二是边缘银行只能连接到核心银行，而边缘银行彼此间不存在借贷关系。实证显示德国的银行间市场网络与CP模型具有很高的拟合度。其研究结论的重要性突显，实际银行间网络结构已经对时下大量基于准ER随机网络或SF网络模型的研究提出了质疑。同时，Finger等[5]实证认为CP结构相比于其他网络模型更好地拟合了意大利银行间网络特性，核心银行数目从金融危机前占比28%减少到危机中的23%，并认为银行间网络结构不服从随机网络模型的原因在于偏好关系型借贷，该观点与Finger和Lux[6]应用行动者导向理论对银行网络演化进行分析的结论相一致。

但是，van Lelyveld和in't Veld[7]的研究与前者观点相悖，他们完全遵循Craig和von Peter实证研究方法，将荷兰银行间市场从1998年到2008年的102家季度数据与德国银行间市场进行对比实证分析，结果显示核心-边缘模型不能很好描述荷兰金融体系的特性。

上述研究都表明，当下已经对基于ER随机网络或无标度网络模型对实际银行间市场体系结构的适用性提出了质疑。而核心-边缘模型提供了一个更佳的参考思路，这正是本文立意所在。本文建模方法的新颖之处在于：一是将基于主体计算经济学理论与复杂网络技术相结合，以贷款风险投资作为数据驱动，使资产负债表模型得以动态生成，回避了统计和计量经济模型所要求的大量时间序列数据的困难；二是提出针对CP银行间网络拓扑结构与无标度SF网络的对比性研究；三是强调仿真银行间市场网络模型的实时性，构建完整银行信贷交易周期，实时分析流动性需求方程，产生贴近现实世界的银行间网络风险敞口头寸。因此，本文所构建的模型能够较好地模拟交易策略或环境条件的改变对银行间市场的影响，为金融宏观审慎监管措施的制定提供理论参考。

2 银行间市场系统性风险模型

2.1 建模背景与思路

本文将模拟一个包括银行、企业、家庭和中央银行四部门及一个银行间市场的简单封闭交易运行体系，假设银行在流动性和资本约束前提下谋求利润最大化。通过投资组合配置对银行微观行为方程的描述，刻画了银行从家庭部门吸收存款D，并提供贷款投资满足企业产出的资金需求；同时，银行为了维持在中央银行准备金存款账户上法定存款准备金余额的要求，即使出现有利的投资机会，而银行又无法筹集到所需资金时，除非选择出售资产，减少企业贷款等行为，否则只能放弃投资机会[8]。银行是否在银行间市场进行同业拆借或拆放，以及向中央银行借款，均需视该银行的流动性需求而定，所以，模型紧密追踪每个银行的流动性，并依此确定其是同业拆放即流动性提供者还是同业拆借即流动性需求者。

接下来，结合银行间网络模型，根据网络生成的银行间借贷连接关系，逐一对每个银行与其邻居节点银行的流动性需求进行匹配，流动性盈余银行按照基本信贷配额机制向流动性需求银行提供需求头寸，对银行间网络债务与债权进行结算，从而确定每个银行的风险敞口。

随后，那些在银行间市场未能得到足够流动性的银行，如果有足够的资产作为担保，满足向中央银行申请流动性需求的条件，就执行获取中央银行流动性的交易程序，进一步向银行间市场中流动性不足的银行提供了头寸需求。而那些没有足够资产的银行，就必须减少投资头寸，同时为了维持资产充足率的监管要求，必须进行资产抛售，可能引发系统性风险，因此，通过对每个银行的偿付能力进行检查，将符合监管最低资本充足标准的银行称之为“活跃”银行，否则为违约银行并将其从银行网络中剔除，重新计算网络敞口。至此，“活跃”状态的银行可向企业实施计划投资，执行投资交易程序，检查企业贷款是否到期和违约，并重新计算银行的流动性，在满足法定存款准备金要求下，更新投资交易。

2.2 资产负债表和流动性的计算

模型假定银行为风险厌恶型和市场价格接受者，其投资组合满足相对风险厌恶效用函数CRRA。其中，向企业的投资I为风险资产，无风险资产为超额存款准备金E。考虑到银行间拆借的实际用途是保障单个银行的流动性，作为银行间贷款流动性的提供者，一般依赖于流动性需求方的主动负债程度，同时拆借双方一般既是流动性需求者又是流动性提供者。所以，模型虽然对银行间网络的敞口进行统计，但并不把银行间贷款纳入到风险投资组合中予以考虑。

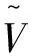
2.2.1 银行决策资产投资组合的配置和规模

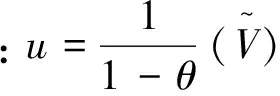
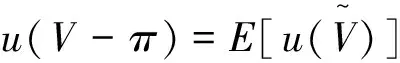
(1)

(2)

其次，为了获得资产投资组合规模，基于方程(2)两边对V微分，得到单位投资组合的边际效用[10]。又因V=E+I，其一阶条件须满足边际效用等于投资组合的再融资成本，即中央银行的基准利率rb，则一阶条件方程为：

最终，银行决策资产投资组合规模近似地为:

(3)

2.2.2 计算银行的流动性

我们把银行间借贷和向中央银行借款两种负债情形纳入两银行模型。对于负债方，一个银行的初始资本金BC在数量上依赖于风险投资I规模与风险权重和法定资本充足率。存款D的初始数值等于资产减去初始资本金，其中存款利率为rd；上缴法定存款准备金rD。按照Totzek[11]理论，在模型中设定了存款提取波动因子δ。存款提取一方面影响法定存款准备金的减少，另一方面如果δ(1-r)D大于超额存款准备金E，则表明银行存在预期流动性不足。

银行间市场的信贷供给Ls和信贷需求Ld对于市场中的银行而言，行为动机因市场拆借利率rb体现出的成本与收益各异。在一个封闭的银行间网络体系内，总体上存在一种均衡：Ld(rb)=Ls(rb)。当rb利率很低时候，银行通常对银行间的借款需求大于银行间贷款的供给，其动机并非作为银行的资产收益，而主要是通过同业拆入增加流动性对实现投资组合的扩张。如果rb利率增加一定水平，银行拆放动机因银行间贷款收益增加，则市场倾向于银行间的贷款供给大于银行间借款的需求。模型假设银行对银行间贷款的需求主要动机是，出于补充短期流动性的原因而不是将银行间贷款作为盈利性的风险资产。所以，主要关注银行间借款Ld作为一种负债的变化，Ld需求的绝对值越大，表明该银行流动性缺口越大。

如果银行有充足的风险资产作为合格担保，那么在模型中设定担保品评级因子β，就可以进一步向中央银行借款Lc。如果担保品不足或者得到中央银行的借款后，银行流动性仍然短缺，此时，银行不得不调整计划风险投资水平，进行资产抛售。

最后，根据银行的资产收益和负债成本支出，上缴中央银行存款准备金的本息，以及包括存款波动，最终得到银行当期t时刻的流动性头寸Qt计算模型：

(4)

其中，(1-δ)Dt-1≤Dt≤(1+δ)Dt-1。

对于仅有两个银行的模型银行间的拆借敞口一目了然，然而，在一个具有N个银行体系中，它们之间错综复杂的银行间负债关系如何描述呢？由此引入了SF网络和CP两种不同拓扑结构银行间市场的网络模型，定义银行彼此之间的债务与债权关系。我们可以网络统计属性并结合上述相关资产和负债动态变化指标，确定银行节点敞口水平，考察系统性风险在不同的银行网络拓扑结构的传染影响程度。

2.3 资产抛售模型

当一个银行的资产组合遭受到一个负向冲击，并且不能达到监管资本水平时候，银行将出售资产以此改善其资本充足率。Cifuentes等[12]为寻求长期非流动资产出售数量与价格之间的均衡状态提供了方法。该资产抛售模型较好地描述了市场出现流动性紧缩时候，较小规模资产抛售引发较大敞口变化的现象。

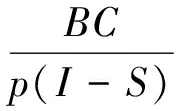
非流动性资产市场价格的发现是通过供给和需求之间均衡调整的“喊价机制”实现。对非流动性资产需求反函数记作：

p=e-α(s)

(5)

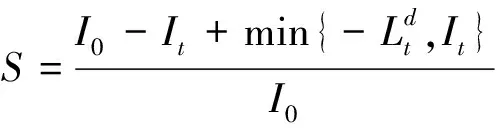
3 银行间核心-边缘网络模型

3.1 网络结构

生成具有CP拓扑结构的网络基本算法一般有两种，区别在于边缘节点与核心节点的连接方法。两种算法都依赖于节点数目、核心节点占比和核心节点之间的连通度，通常我们通过遍历每个节点，如果设定连接到核心节点概率为P，则剩余边缘节点的概率为1-P，而核心节点之间按照随机拓扑结构进行连接。本文采用Borgattiand Everett[13]的随机依附算法将边缘节点与核心节点连接。银行节点数目N=50，核心节点数目为8，核心节点之间的连通度为80%。

从这两个不同结构网络中节点的特征向量中心度[14-15]排序表(见表1)可以发现，CP网络中前8个银行节点的特征向量中心度远远大于排在其后的银行_9的数值，而SF网络中的第8个银行节点与紧排其后节点的数值并不存在跳跃性差距。虽然CP网络特征向量中心度的整个网络均值小于SF网络，但是，就前8个核心银行而言，CP网络特征向量中心度的均值为47.685，大于SF网络前8个银行节点均值37.503。因此印证了CP网络中边缘银行节点与处于核心银行之间的拆借数量相比于SF网络更为集中。

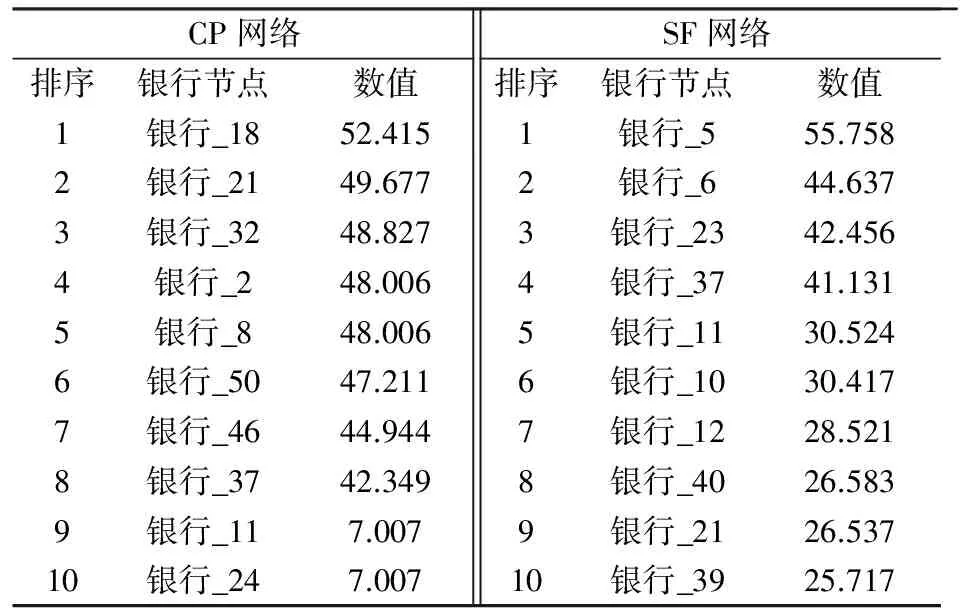
表1 特征向量中心度的排序表

注：两个网络模型中银行节点标号随机生成。

3.3 银行网络敞口与可得流动性

由前述建模思想可知，确定银行间每个银行的敞口水平的前提，在于银行间网络必须存在资金盈余方银行和流动性资金需求方银行，因此首先要计算银行的流动性需求。一个银行流动性需求水平的确定，须根据银行资产负债表每个账户实际交易数据。模型假设整个银行网络体系总的资产数量固定，并平均分配于每个银行，根据公式(3)得出每个银行的计划最优投资结构与规模，则最优风险投资计划规模Ip和无风险的超额准备金计划规模Ep也可以事先确定。因为每个银行的资产负债表模型中的投资账户I，都赋予了贷款成功率、贷款利率以及随机产生的贷款期限等参数，所以一旦银行资产负债表的初始化，首先对每个银行的风险投资账户中贷款期限进行计算并判断是否逾期违约，再依据起初的风险计划投资规模、到期贷款利率和贷款损失率重新计算并得到当期的投资头寸I。因此，每个银行的资产负债中各个不同的交易账户随之就发生变化，其初始流动性头寸Q0计算由公式(4)可得。

在银行间网络模型初始化之前，模型进行了资产负债表模型的初始化，每个银行的计划流动性需求头寸包括银行间市场借款和向中央银行借款的两个需求资金来源，数值上等于：Lp=Ld+Lc=Q0-((Ip-I)+(Ep-E))，且Lp>0表示银行有过剩的流动性；否则，表示银行为流动性需求方。

假设流动性需求方银行首先在银行间市场进行资金筹集，此时银行间网络模型初始化，进行银行间借款交易结算。一个流动性需求银行的实际头寸，应该由与其有直接连接关系的邻居银行节点提供，且这些直接邻居银行节点必须有过剩的流动性，一旦匹配就按照最简单的信贷配额机制提供需求头寸，具体计算方法为：

Ld=min{-Ld,∑Ls|Ld·Ls<0ifLd<0} 按照以上公式遍历银行间网络模型的所有节点，即可得银行间的网络敞口。

而后，对所有银行间网络的节点银行进行偿付能力检查，若银行资本比率满足：BC/I≥r*，则该银行为活跃银行。其中，这些银行仍然有流动性需求Ld，并且银行的风险投资头寸I>0，那么，该银行向中央银行的借款头寸为：Lc=min{I·β,|Ld|}。

最后，我们要考虑那些不具有从中央银行借款条件的银行，这些银行首先对计划投资规模进行消减，查看当期的流行性需求：Lp=Ip-I；如果Lp<0，说明银行仍然存在流动性需求缺口，为了达到监管资本水平，银行不得不进行资产抛售。具体清算价格与清算规模由公式(5)可得。

以上描述了银行获取可得流行性的过程，最终要将可得资金投向企业，实施贷款投资计划，检查贷款投资期限是否违约，对新一轮投资交易进行更新。同样，因为银行流动性发生变化，超额存款准备金相应也要调整。

4 仿真与经济分析

本文将通过较多的参数设置，模拟信用损失造成的流动性不足与资产抛售等压力困境，通过跟踪分析银行间拆借及向中央银行借款的情况，考察系统性风险对具有不同拓扑结构的银行网络体系的冲击影响作用以及最终银行的风险分担和系统恢复力。

4.1 算法执行步骤说明

第一步，实现银行环境初始化。包括以下步骤：

1.根据第2.2.1节的描述和公式(2)首先计算最优投资规模；

2.在第一步基础上动态生成银行节点的资产负债表：1)生成投资交易追加至银行的投资账户I；2)计算并追加至超额存款准备金账户E；3)计算并追加至银行的资本金账户BC；计算家庭部门的存款并追加至银行的储蓄账户D；4)计算并追加至银行的法定存款准备金账户rD；最后，计算并追加至银行的中央银行贷款账户LC。直至所有银行节点赋值完毕。

第二步，实现网络环境初始化。根据成熟的复杂网络算法可以分别加载无标度网络和核心-边缘网络模型。因为在银行间网络模型初始化之前，模型进行了资产负债表模型的初始化，根据正文第3.3节的描述公式遍历银行间网络模型的所有节点，即可得银行间的网络敞口。

第三步，对每个银行的风险投资账户中贷款期限进行计算并检验判断是否逾期违约，计算银行投资合约到期的损失。

第四步，重新计算并得到当期的投资头寸I，每个银行的资产负债中各个不同的交易账户随之更新。

第五步，更新银行间网络敞口。

第六步，对所有银行间网络的节点银行进行偿付能力检查，若银行资本比率满足：BC/I≥r*，则该银行为活跃银行。否则，记为失败银行节点。

第七步，对活跃银行进行流动性需求计算，判断是否具有向中央银行的借款头寸。否则，那些仍然存在流动性需求缺口的银行不得不进行资产抛售。

第八步，返回步骤三，对新一轮投资交易进行更新。

最后，根据自定的模拟循环次数退出执行过程，并得到失败银行节点的数量及其相关交易数据。

为了对实际经济情况进行仿真，本文模拟一个银行规模N=50的银行间网络体系，研究时间跨度τ=1000个工作日周期，设置银行可得企业贷款总资产交易数目为Atotal=100。其中，单个银行每笔最优投资组合为V/2，最优投资结构和规模依赖于其风险规避程度系数θ，θ的取值范围[16]须保证每个银行的投资组合中都持有无风险投资超额存款准备金资产。本文模型关注源于银行资产质量变化所引起的流动性不足及失去偿付能力等银行失败情形。模型中每个银行的资产负债表的动态变化依赖于银行投资企业贷款成功概率Pfirm。所以，在模型研究时间周期内，经企业贷款期限mfirm参数的设定，则将1-Pfirm企业贷款交易作为逾期贷款，并假定违约贷款的损失率为100%，以此作为压力情景风险来源。通过不同压力情景设置，模型可以最终得到银行间借款、向中央银行借款交易数据变化状况，以及因资本损失成为不活跃银行的结果。

4.2 仿真一：基准情景

为便于考察系统性风险影响规模和程度，首先设置一种处于正常经济状态下的基准情景作为参照基准。参数设定如下：存款波动因子δ=0.01，最低监管资本充足率r*=8%，担保品评级因子β=80%，法定存款准备金率r=2%。每笔企业贷款期限将随机产生，且最长为mfirm=500个工作日，模型运行500个工作日后，所有银行的投资资产将全部清算，而企业贷款成功概率在整个模型运行周期为Pfirm=99%，即企业实际违约概率只有1%。将以上参数代入模型分别在CP网络和SF网络两种不同的银行间网络模型中运行之后，得到如下结果：

图1显示了最终活跃银行数目的平均结果。CP网络模型活动银行数目43家，显然大于SF网络模型的41.5家。SF网络模型的失败银行数目，要多于CP网络模型。

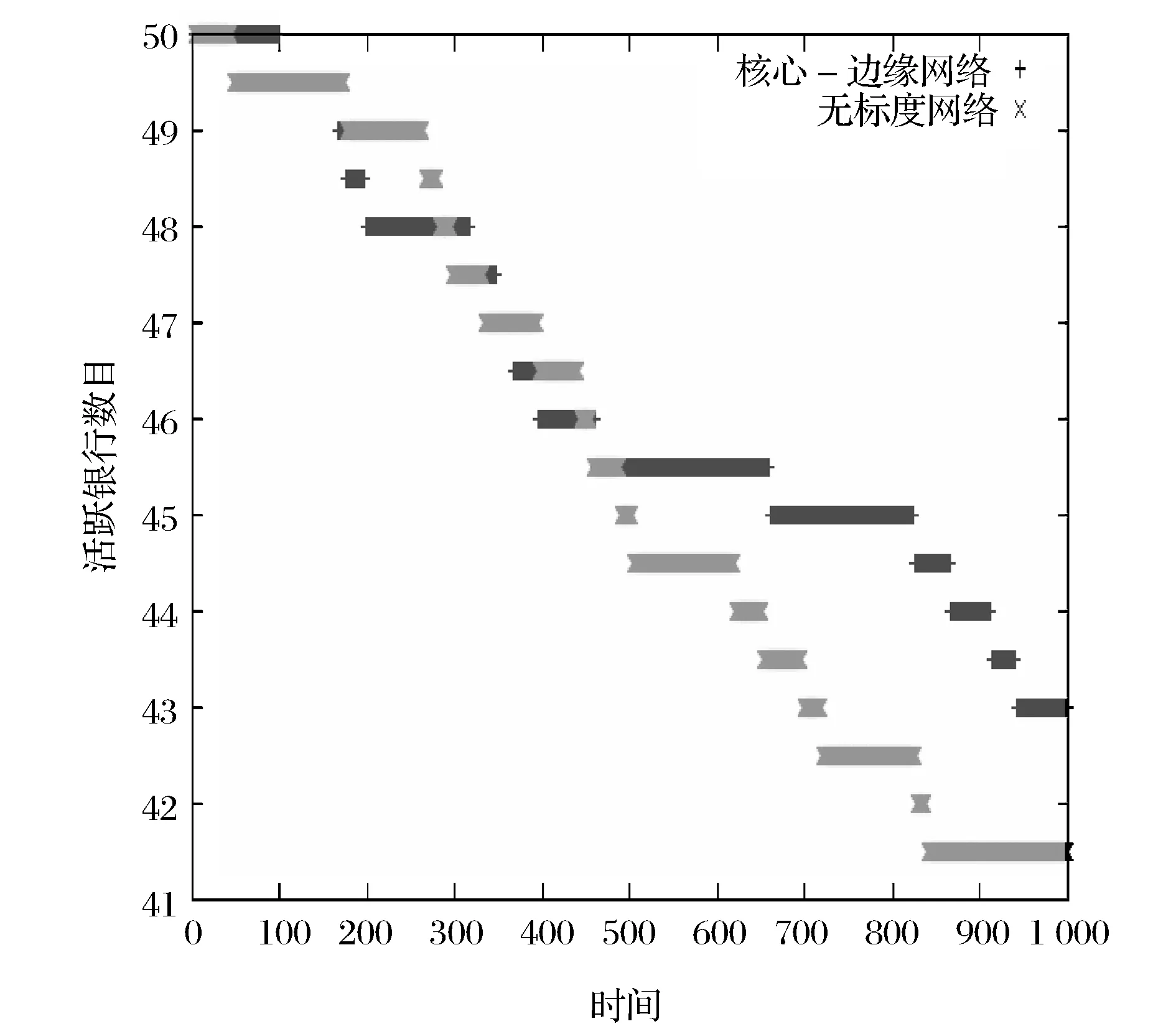
图1 活跃银行数目(仿真一)

从图2中可以观察到，SF网络模型中银行间拆借交易数量要远大于CP网络模型。模型运行到500个工作日后，CP网络模型中的银行间借款交易几近停滞，而SF网络模型也陡然减少。原因在于SF网络的网络密度远大于CP网络统计指标的差异。

图2 银行间借款数量(仿真一)

图3 向中央银行借款数量(仿真一)

从图3中发现，CP网络中银行向中央银行借款数量要高于SF网络。由表1可知，CP网络分层特征突出，核心银行的特征向量中心度的均值大于SF网络的前8个网络银行节点。所以，CP网络模型中满足向中央银行借款条件的银行节点要多于SF网络模型情形。这也是CP网络中银行的失败数量小于SF网络的原因。

4.4 仿真二：资产抛售压力情景

在仿真一的基础上，仅将企业初始投资成功率从99%下调到500个工作日后的95%，即1%不良贷款率上升到5%，其他参数环境与仿真一相同。因企业投资成功概率的降低，造成银行的资本损失与流动性缺失，通过银行间市场形成了银行间传染风险，致使更多银行出现资本损失，低于最低监管资本要求水平。为此，我们考虑资产抛售压力情景，考察那些为了维持最低监管资本充足率的银行所进行的资产抛售行为对整个银行体系的冲击状况。在出现传染风险压力情景基础上，再引入表示资产抛售压力状况的资产清算贴现因子α=0.9，即资产抛售价格下跌深度为90%。在两种冲击风险叠加作用下，模型运行最终的活动银行数目结果如图4所示。

图4 活跃银行数目(仿真二)

与仿真一的结果比较，CP网络中活跃银行数量锐减为13家；SF网络体系中的活跃银行数目也降至16家。由于失败银行数量的增加，整个银行体系无论是银行间借款还是向中央银行借贷的交易数量都将大幅减少，如图5和图6所示。

图5 银行间借款数量(仿真二)

图6 向中央银行借款数量(仿真二)

模型中实施资产抛售行动的银行，都是指那些仍有偿付能力活跃银行，但因在银行间借贷和中央银行借款之后，依然存在流动性缺口的银行，它们不得不消减投资组合中的风险投资计划，抛售银行投资交易账户的资产份额。如果一个银行的资本金足够承受非银行部门的信用损失和其他银行敞口造成的减计损失的时，但由于资本消减，进而不足以支撑因为其自身资产抛售或其他银行资产抛售引发的盯市价值损失，结果导致银行体系出现资产抛售的传染性违约。

4.5 仿真测试三：两种逆周期策略的比较

第一种方法是逆周期调整监管资本水平。基于上述资产抛售压力情景的基础上，为了考察监管当局救赎策略效果的显著性，将法定监管资本充足率从原来整个测试周期为8%调整至假想运营状态20%，理论上逆周期调整资本充足率可以缓释系统性风险，考虑到仿真二的压力情景，在系统实现初始化2个工作日之后，故将法定监管资本充足率降低到6%。最终运行结果如图7所示。

图7 活跃银行数目(仿真三)

第二种方法采取放松中央银行借款的担保品评级条件。基于上述资产抛售压力情景的基础上，将资产担保品评级因子从原来的β=0.8，放松至β=0.95。意味着中央银行将银行的资产质押条件放宽，满足向中央银行借款条件的银行数量也会增加，改善银行的流动性头寸紧张的状况。那么，CP网络中核心银行将会有更多机会免予陷入失败境地。因为CP网络中核心银行的特征向量中心度比SF网络体系要高，所以更希望仿真结果出现，CP网络体系失败银行数量减少，其改善程度要强于SF网络的情形。最终运行结果如图8所示。

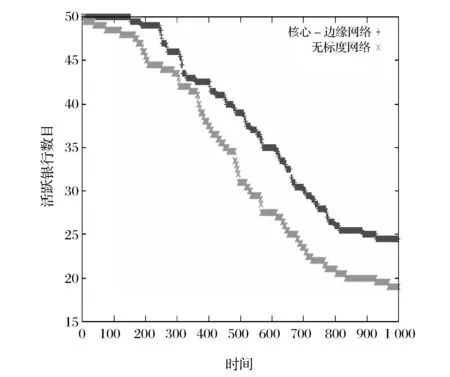
图8 活跃银行数目(仿真三)

从图7显示的活跃银行数目结果发现，CP网络中活跃银行数量从原来的仅有13家，恢复到现有的27家，同时，SF网络体系中的活跃银行数目从原有的16家也上升到23家。可见，逆周期调整监管资本的风险缓释策略对于两种不同银行间网络拓扑结构都是有效的。显然，CP网络结构体系对于风险缓释策略的敏感性更强。

从图8的结果可见，CP网络中活跃银行数量从13家上升至现在的24家，同时，SF网络中的活跃银行数目从原有的16家，仅仅恢复到目前的18家。可见，放松中央银行借款的担保品评级的缓释策略对于SF网络而言，其敏感性和恢复力效果都比CP网络体系结构差。

对比两种缓释政策效果，逆周期调整监管资本水平对于两种不同的银行间网络拓扑体系都是有效的，而放松担保品评级条件的方法对于SF网络体系效果不显著。因此，逆周期调整监管资本水平的方法要优于放松中央银行借款的担保品评级条件的方法。

5 结语

本文模拟环境中的每一个异质性银行主体都具有不同投资组合结构和动态资产负债表，通过考察银行对企业的信贷投资交易活动，建立了银行间流动性需求头寸方程，结合CP结构和SF结构两种银行间网络模型，产生了网络敞口数据。引入源于信贷损失的流动性不足和资产抛售两种共同冲击传播机制，通过模型参数设置不同的金融困境压力情景，深入分析了系统性风险对具有不同拓扑结构的银行网络体系的冲击影响作用。同时，模型将中央银行也作为参与者主体，探讨了监管当局缓释系统性风险的政策工具效果。

与已有相关文献相比较，通过模型的仿真测试与结果分析，本文在银行间网络体系的稳健性与系统性风险宏观审慎管理方面，有以下结论性认识：

第一，面临资产损失造成的流动性缺失的共同冲击时，从银行间市场借贷数量的运行结果来看，无论在CP结构网络还是SF网络结构体系中，绝大多数的拆借交易数量集中出现在最长信贷资产期限完全到期即500个工作日周期之前。其后，交易量逐渐大幅减少，或交易停止。对应同期的活跃银行数目的运行结果，两种银行网络体系中银行活跃数量减少幅度都较小，表明了银行间市场为银行体系缓解流动性风险冲击起到了缓冲和稳定作用。

无论在CP结构网络还是SF网络结构体系中，大量向中央银行借款的交易出现在500个工作日周期之后，直到整个模拟周期结束。因此，中央银行提供的贷款流动性是对银行间市场流动性头寸供给之后的补充。然而，在面临资产损失造成的流动性缺失与资产抛售压力情景下，500个工作日周期之后，CP结构网络与SF网络结构体系中活跃银行数目都出大幅锐减，所以，中央银行提供的贷款流动性对其后出现的传染性风险的缓释作用并不明显。

由于SF网络体系中的银行间交易数量规模大于CP结构网络，所以，从活跃银行数目的运行结果图形来看，CP结构网络中活跃银行数目的下降速度快于SF网络结构体系，表明网络密度大的、银行间交易数量高的SF网络体系，在承受冲击时风险分担性和系统稳定性上强于CP结构网络。

第二，在面临资产损失造成的流动性缺失与资产抛售压力情景下的共同冲击时：放松中央银行借款的担保品评级条件的措施对于SF网络而言，其敏感性和恢复效果都比CP网络体系差；而逆周期调整监管资本水平的策略对于两种不同银行间网络拓扑结构都是有效的。总体而言，CP网络体系对于缓释策略工具的敏感性和恢复力表现更强。

第三，虽然CP网络银行体系易于遭受系统性风险，但从宏观审慎管理角度看，体现出对逆周期策略工具的敏感性和体系恢复力强的优势；从识别系统重要性机构的简便性上看，由于拓扑结构的独特性，CP网络相比于SF网络体系更加容易，并且需要救赎的具有系统重要性银行的数量也更少。所以，在监管资源配置有限条件下，CP结构银行网络体系更加利于监管当局和中央银行的监管与救赎。

[1] Allen F, Gale D. Financial contagion[J], Journal of Political Economy，2000， 108(1)：1-33.

[2] Freixas X, Parigi B M, Rochet J. Systemic risk, interbank relations and liquidity provision by the central bank[J]. Journal of Money, Credit and Banking,2000, 32 (3), 611-638.

[3] Teteryatnikova M. Resilience of the interbank network to shocks and optimal bail-out strategy: Advantages of "tiered" banking systems[R]. Vienna Economics Papers 1203, University of Vienna, Department of Economics, 2012.

[4] Craig B, von Peter G. Interbank tiering and money center banks[R]. Journal of Financial Intermediation,2014,23(3):322-347.

[5] Finger K, D Fricke, T Lux. The italian interbank network:An overview[J]. In progress, Kiel Insitute for the World Economy, 2012.

[6] Finger K, T Lux. The evolution of the banking network:An actor-oriented approach[J]. In progress, Kiel Insitute for the World Economy, 2011.

[7] van Lelyveld I, in 't Veld D. Finding the core: Network structure in interbank markets[R]. Journal of Banking & Finance,2014,49:27-40.

[8] Peng Xingyun. Liquidity, liquidity excess and monetary policy [J]. Economic Research Journal,2007,(11):55-70

[9] Pasche M. Interbank lending and the demand for central bank loans-A simple microfoundation[R]. Jena Economic Research Papers Friedrich-Schiller-University Jena, Max-Planck-Institute of Economics, 2010.

[10] Pasche M. Fundamental uncertainty, portfolio choice, and liquidity preference theory[R]. Jena Economic Research Papers,Friedrich-Sehiuer-University Tena,Max-Planck-Institute of Econornics,2009.

[11] Totzek, Alexander. The bank, the bank-run, and the central bank: The impact of early deposit withdrawals in a new Keynesian framework[R]. Working Papers, Christian-Albrechts-University of Kiel, Department of Economics, 2008.

[12] Cifuentes R, Shin H S, Ferrucci G. Liquidity risk and contagion[J]. Journal of the European Economic Association, 2005,3(2/3):556-566.

[13] Borgatti S P, Evertt M G. Models of core/periphery structures[J]. Social Networks, 2000,21(4):375-395.

[14] Freeman L C. Centrality in social networks: conceptual clarification[J]. Social Network, 1979,1(3):215-239.

[15] Wasserman S, Faust K. Social network analysis: Methods and applications[M]. Cambridge:Cambridge University Press, 1994.

[16] Yang Chaojun. Parameter uncertainty and investor’s portfolio choice: Evidence from China stock market [J]. Chinese Journal of Management Science,2008,16(3):37-43.

Studyon Multi-agent Models Analyses for Systemic Risk from the Interbank Network

DENG Chao1, CHEN Xue-jun1,2

(1.Business School of Central South University, Changsha 410083, China；2.Zhengzhou Training Institute,The People’s Bank of China, Zhengzhou 450011, China)

In this paper a multi-agent model which analyses for systemic risk from the core-periphery structure in interbank network is proposed. Our model consists of a network of banks, which endogenously determine their optimal portfolio allocation by maximizing profits subject to liquidity and capital constraints. For the simulation framework to be useful for assessment of central bank policy, banking firm behavioral responses must be modelled in the context of interbank market conditions and with automated access to balance sheet and network exposure data to anchor the financial decisions being simulated. Different possible network structures are compared, while interbank markets network with the core-periphery topology is more susceptible to common shock and contagion than scale-free network, it tend to be more resilient to financial distress than others under macroprudential regulation and policy regime.

multi-agent model；interbank markets；systemic risk；core-periphery network; common shock

1003-207(2016)01-0067-09

10.16381/j.cnki.issn1003-207x.2016.01.008

2013-07-14；

2014-09-09

国家自然科学基金资助项目 (71173241)；教育部新世纪人才基金( NCET-10-0830)

简介：陈学军(1969-)，男(汉族)，河南开封人，中南大学商学院博士研究生，中国人民银行郑州培训学院，研究方向：宏观审慎管理、金融工程，E-mail:chenxuejun@pbcti.cn.

F830.9

A