问 题 1830 的 研 究

青海师范大学教育硕士 (225700)

朱云燕



问 题 1830 的 研 究

青海师范大学教育硕士 (225700)

朱云燕

1.问题的提出

《数学通报》问题1830：

命题人刊登的解答曲折繁复，与问题简单优美的形式颇不相配，下面我们将给出此题的简证，并从其等价形式出发进行深入研究．

2.问题的别证与推广

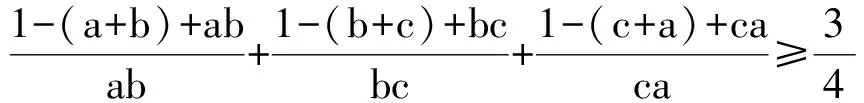
下面我们将(2)推广为：

推广 a,b,c∈R+，且a+b+c=s．则有

事实上，(3)⟺2(a+b+c)(a2+b2+c2)+9abc≥(a+b+c)3⟺a3+b3+c3+3abc≥a2b+b2c+c2b+b2c+c2a+a2c，将Schur不等式a(a-b)(a-c)+b(b-a)(b-c)+c(c-a(c-b)≥0展开即得a3+b3+c3+3abc≥a2b+b2c+c2b+b2c+c2a+a2c，故不等式(3)成立．

在(3)中取s=2即得(2)．

3.问题的类似联想

我们先给出与不等式(3)结构相似的一个反向不等式：

联想1 a,b,c∈R+，且a+b+c=s．则有

我们再给出与不等式(3)形似的一个同向不等式：

联想2 a,b,c∈R+，且a+b+c=s．则有

4.问题的深入研究

在a,b,c∈R+，且a+b+c=s的条件下，下面我们进一步考虑a2+b2+c2+λabc(λ∈R)的取值范围．

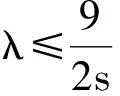
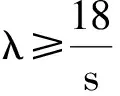
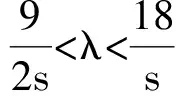
因为a→s,b=c→0时，a2+b2+c2+λabc→s2，故上界s2是最佳的，不可改进．