解中点弦问题的利器——“点差法”

江西省余干二中 (335100)

章华锋



解中点弦问题的利器
——“点差法”

江西省余干二中 (335100)

章华锋

分析：本题涉及到直线被椭圆截得弦的中点问题，采用点差法和中点坐标公式，运算会更为简便．

点评：运用点差法,可以求中点弦所在的直线方程.本题中，中点弦方程是明确存在的，如果结果是问中点弦方程是否存在，则还要把求出的直线方程与圆锥曲线方程联解，看它的判别式是否大于零.

例2 已知抛物线y2=6x，求过点(0,1)直线被抛物线所截的弦的中点轨迹方程.

分析：可以假设出中点的坐标，通过中点公式与斜率公式得出一个与中点坐标有关的一个方程.

点评：用点差法，可以求出平行弦或过定点弦中点的轨迹问题.

分析:本题可以利用中点坐标公式与斜率公式的条件，列出方程，解方程组.

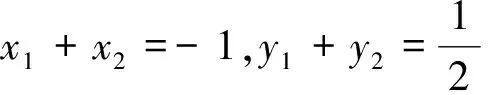
点评：在运用点差法，求圆锥曲线的轨迹方程时，要充分运用已知条件(中点坐标公式、斜率公式)，列出方程，再运用待定系数法求出圆锥曲线方程.

分析：本题中两点关于直线对称，是有关中点的问题，可以考虑使用点差法.

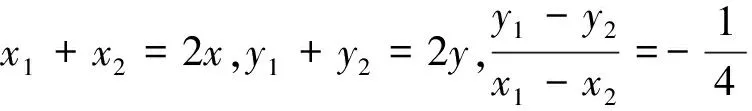
点评：解决这类问题有两种思路：一是先求出直线斜率的变化范围进而求出参数的取值范围；二是借助曲线方程中变量的取值范围求出参数的取值范围.

分析：本题中有“B是线段PQ的中点”可以考虑使用点差法．

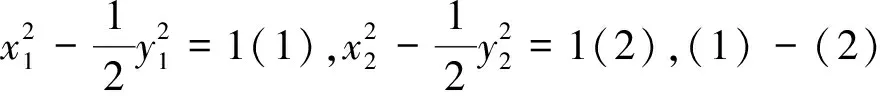
点评：这是一个开放性命题，可以先假设k存在，再通过计算来确定k是否能存在．