一道2016摩尔多瓦数学奥林匹克试题别解及推广
2016-12-17江苏省姜堰中等专业学校225500
中学数学研究(江西) 2016年12期
江苏省姜堰中等专业学校 (225500)
陈 宇
一道2016摩尔多瓦数学奥林匹克试题别解及推广
江苏省姜堰中等专业学校 (225500)
陈 宇
2016摩尔多瓦数学奥林匹克试题
已知a,b,c是满足a2+b2+c2+ab+bc+ca=6的正数,求a+b+c的最大值.
笔者在此给出两个别解.
(法二)∵a,b,c是正数,由已知得6=a2+b2+c2+ab+bc+ca≥2(ab+bc+ca)⟹ab+bc+ca≤3,又a2+b2+c2+ab+bc+ca=6⟺(a+b+c)2=6+(ab+bc+ca)≤6+3=9⟹a+b+c≤3.
法一主要依据均值不等式适当放缩;法二则主要借助题设条件(也需依据均值不等式)适当变形再进行放缩,并求解.较之文[1],此两法思路更显自然,无需技巧.
进而该赛题可推广如下:
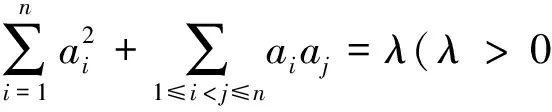
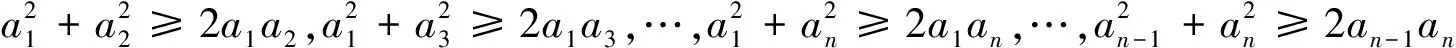
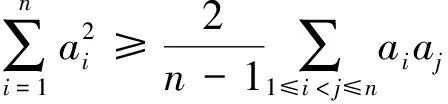
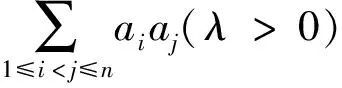
[1]周辉.2016年IMO不等式题的巧思妙解[J].中学数学研究(江西),2016,5(49~50).
