一道中考题与一道高考模拟题的同源探究

福建省泉州市第三中学 (362000)杨秋环福建省泉州市第五中学 (362000)

杨苍洲



一道中考题与一道高考模拟题的同源探究

福建省泉州市第三中学 (362000)杨秋环福建省泉州市第五中学 (362000)

杨苍洲

图1

(1)求h的值；

(2)通过操作、观察，算出△POQ面积的最小值(不必说理)；

(3)过点P、C作直线，与x轴交于点B，试问：在直线l的旋转过程中，四边形AOBQ是否为梯形？若是，请说明理由；若不是，请指出四边形的形状．

题2 (2013年福建省高考模拟)某同学用《几何画板》研究抛物线的性质：打开《几何画板》软件，绘制某抛物线E:y2=2px，在抛物线上任意画一个点S，度量点S的坐标(xS,yS)，如图2．

(1)拖动点S，发现当xS=4时，yS=4，试求抛物线E的方程；

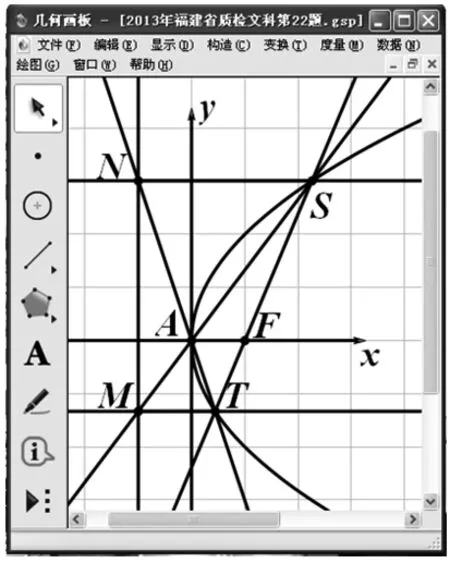
图2

(2)设抛物线E的顶点为A，焦点为F，构造直线SF交抛物线E于不同两点S、T，构造直线AS、AT分别交准线于M、N两点，连接直线MT、NS．经观察得：沿着抛物线E，无论怎样拖动点S，恒有MT∥NS.请你证明这一结论；

(3)为进一步研究该抛物线E的性质，某同学进行了下面的尝试：在(2)中，把“焦点F”改变为其它“定点G(g,0)(g≠0)”，其余条件不变，发现“MT与NS不再平行”．是否可以适当更改(2)中的其它条件，使得仍有“MT∥NS”成立？如果可以，请写出相应的正确命题；否则，说明理由．

1.3.1 诱捕器试验 试验设A、B、C 3个处理，每个处理设5次重复，各小区随机排列。将3种诱捕器同时安装到茶园，诱捕器离茶丛表面20 cm，各小区之间间距10 m，配备北京中捷四方生物科技股份有限公司茶尺蠖诱芯，比较3种诱捕器在试验期间的诱捕量。试验时间为2017年7月11日至8月2日，每周调查1次，连续调查4周。图1为3种茶尺蠖诱捕器。

2.题源探究

上述两道试题，一道面向初中毕业生，一道面向高中毕业生.从表象上看，似乎风马牛不相及，而实际上它们却有共同的题源，有着相同的数学本质.两道试题都是源于抛物线的定性性质，经过命题者的巧妙包装、设计，编制成分别适用于中考考生和高考考生的试题.为加深对试题的理解，笔者探究了抛物线的这一性质.

抛物线的性质1 已知抛物线E:y2=2px的顶点为O，焦点F，准线为l.直线m过F，与E相交于A,B两点，点A′,B′在l上.若AA′∥BB′∥x轴，则A,O,B′三点共线，B,O,A′三点共线；反之，若A,O,B′三点共线(或B,O,A′三点共线)，则AA′∥BB′∥x轴.

进一步推广抛物线的性质，把“焦点和准线”一般化后我们能得到下述命题：

抛物线的性质2 已知抛物线E:y2=2px的顶点为O，直线m过G(g,0)，与E相交于A,B两点，点A′,B′在l:x=-g上.若AA′∥BB′∥x轴，则A,O,B′三点共线，B,O,A′三点共线；反之，若A,O,B′三点共线(或B,O,A′三点共线)，则AA′∥BB′∥x轴.

(1)若AA′∥BB′∥x轴，则A′(-g,y1),

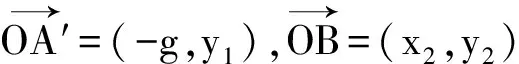
同理可证，B,O,A′三点共线.

同理可证：AA′∥x轴.

若B,O,A′三点共线，同理可证AA′∥BB′∥x轴.

3.圆锥曲线的统一性质

著名的数学教育家波利亚曾形象地指出：“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个.”通过上面的探究，我们知道，抛物线具有性质1，2，那么在椭圆、双曲线中是否也有相似的几何性质呢？回答是肯定的，我们在下面给出椭圆和双曲线的性质，证明从略.

*本文由四川师范大学2017届研究生优秀学位论文培育基金项目资助.