基于新息估计和正交投影的闭环子空间模型辨识

侯杰 刘涛

基于新息估计和正交投影的闭环子空间模型辨识

侯杰1刘涛1

针对闭环控制系统提出一种基于新息估计和正交投影的闭环子空间模型辨识方法.首先采用最小二乘法对VARX模型(Vector autoregressive with exogenous inputs model)进行计算得到新息估计值,然后通过将由观测输入输出数据构造的Hankel矩阵正交投影到新息数据的正交补空间以消除噪声影响,从而在无噪声的输入输出数据奇偶空间中提取得到扩展可观测矩阵和下三角形Toeplitz矩阵.最后采用平移变换法得到系统矩阵.对该算法严格分析和证明了实现一致估计的条件.通过仿真实例验证了本文方法的有效性和优越性.

子空间辨识,闭环辨识,奇偶空间,新息估计,正交投影,一致估计

子空间辨识算法由于能对多输入多输出系统采用统一框架建立状态空间模型,在系统辨识和控制工程领域受到广泛关注[1].有一些子空间算法被提出用于开环辨识工业过程,得到一致估计结果[2].但是,由于过程操作安全性和稳定性的需要,许多工业过程限制在闭环条件下进行辨识实验,由于反馈控制作用的影响,使得过程噪声和输入存在相关性,使得传统开环子空间方法产生辨识偏差[3].闭环系统辨识因此在近年来受到很多关注和探讨[4],一些闭环子空间辨识算法被相继提出[5].这些算法可被归纳为三类,第一类方法[6−7]采用辅助变量策略消除噪声影响,保证估计结果的一致性;第二类方法[8]采用最小二乘法对高阶VARX模型(Vector autoregressive with exogenous inputs model)进行计算得到马尔科夫估计参数,由于VARX模型只包括当前时刻的不可测噪声,该噪声和VARX模型的过去时刻输入无关,从而可保证所得参数的一致性;第三类算法[9]用噪声预估值代替真实值进行计算保证得到一致估计结果.

基于奇偶空间的闭环子空间辨识算法SIMPCAwc[6]采用过去时刻输入输出数据作为辅助变量来消除噪声,以得到无噪声的输入输出数据,然后从无噪声影响的输入输出数据奇偶空间中提取得到扩展可观测矩阵和下三角形Toeplitz矩阵,从而求得系统矩阵,该方法取得较好辨识精度.然而,文献[7]指出当闭环系统设定点输入激励为不相关白噪声序列时,虽然引入辅助变量与噪声不相关,可以有效地消除噪声,但由于该辅助变量和系统设定点输入激励也不相关,导致从无噪声输入输出数据奇偶空间中提取参数可能同时含有过程模型参数信息和控制器参数信息,因而无法对它们进行区分,从而致使过程模型估计出现偏差.针对SIMPCAwc[6]辨识方法存在的问题,本文通过将输入输出数据正交投影到新息数据的正交补空间来消除噪声,以得到新的无噪声数据矩阵,进而从其对应的奇偶空间中提取得到扩展可观测矩阵和下三角形Toeplitz矩阵.由于新息数据的正交补空间数据和噪声无关,且同时与系统设定输入激励相关,确保本文方法从新的无噪声奇偶空间中提取的参数只包含过程模型参数,有效地保证估计结果的一致无偏性.由于新息数据为不可测量数据,本文通过模型推导,得到和待辨识状态空间模型等价的VARX模型.在此基础上,采用最小二乘法对VARX模型进行计算以得到新息的一致估计值.采用新息一致估计值代替真实值,以完成模型参数估计.为了论证说明本文方法的有效性,严格分析和给出了本文算法保证一致估计的条件.

1 问题描述

本文研究如下线性离散状态空间过程模型:

其中,x(t)∈Rnx,u(t)∈Rnu,y(t)∈Rny分别为系统状态和过程输入和输出.v(t)∈Rny和w(t)∈Rnx分别为过程测量噪声.A,B,C,D分别为相应维数的系统矩阵.本文研究系统在闭环工作条件下,利用系统输入和输出观测数据,辨识对象状态空间(亦称子空间)模型.

由于闭环反馈控制作用的影响,使得过程测量噪声和输入存在相关性,若直接通过模型(1)来辨识系统矩阵,很难消除噪声对辨识结果的不利影响.因此,采用卡尔曼滤波原理[10],将系统模型(1)等价表示为新息形式

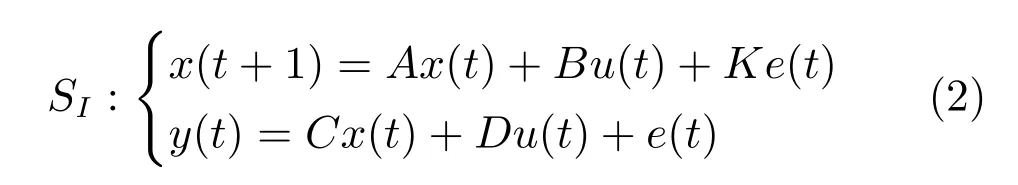
其中,K为卡尔曼滤波增益,新息e(t)为零均值白噪声,当i＜j时,新息e(j)和输入输出{u(i),y(i)}不相关.

定义过去和将来水平数分别为p和f,过去和将来输入向量分别为up(t)=[u(t−p)T···u(t−2)Tu(t−1)T]T和uf(t)=[u(t)T···u(t+f−2)Tu(t+f−1)T]T,定义过去和将来输入Hankel矩阵Up=[up(t)T···up(N)T]T和Uf=[uf(t)T··· uf(N)T]T,输出和新息数据做类似定义.

对式(3)进行迭代可得:

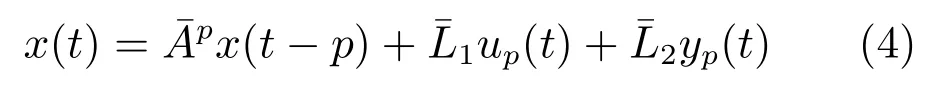
本文将采用模型(2)和(5)对系统矩阵进行辨识.定义Xp=[x(t−p)···x(t−p+N−1)]和Xf=[x(t)···x(t+N−1)].通过对式(2)进行迭代可得:

其中,扩展可观测矩阵为Γf= [CT··· (CAf−1)T]T.下三角形Toeplitz矩阵分别为

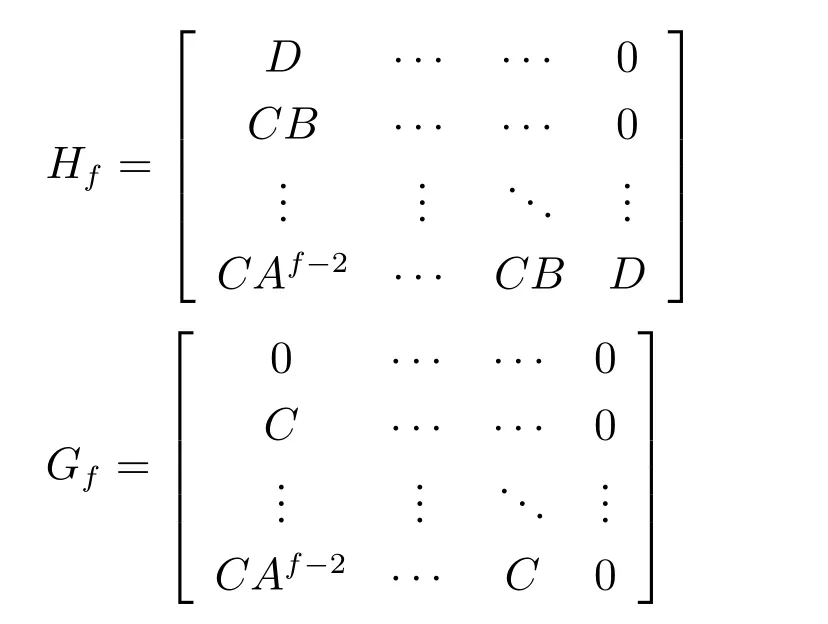
2 闭环子空间辨识算法和一致性分析

2.1 闭环子空间辨识算法

在式(6)的基础上,通过同时计算扩展可观测矩阵Γf和下三角形Toeplitz矩阵Hf实现对系统矩阵的辨识.首先将输入数据移至式(6)的左侧,得到:

为求解式(7)得到Γf和Hf的估计值,需要消除未知状态和新息的影响.通过在式(7)的左右侧同时引入Γf的正交补向量由于

通过将式(8)正交投影到Ef的正交补空间来消除新息噪声,

采用最小二乘法可得Hf1的一致估计如下:

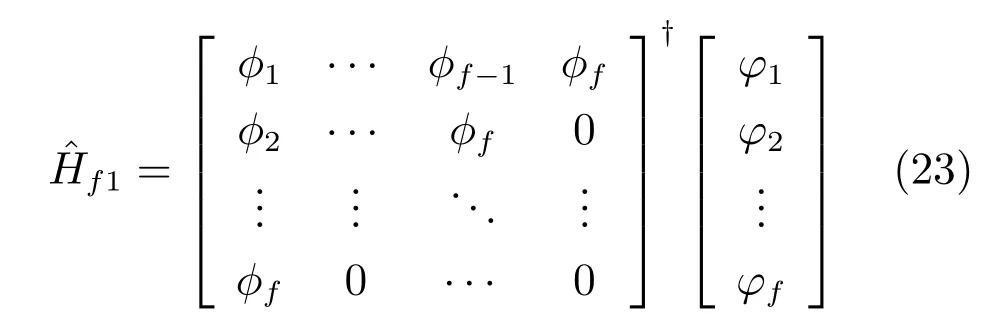
本文基于新息估计和正交投影的闭环子空间辨识方法(Closed-loop subspace identification method using innovation estimation and orthogonal projection,CSIMIEOP)可总结如下:

步骤2.通过SVD分解对式(15)进行计算.

步骤4.通过式(24),式(25)和式(27)求解系统矩阵

2.2 闭环一致条件分析

由第2.1节闭环子空间辨识算法可知,本文采用新息估计和正交投影消除噪声,得到一致估计结果.辨识结果是否一致取决于是否一致,本文对它们的一致估计条件进行分析和说明,给出如下定理.

定理1.若

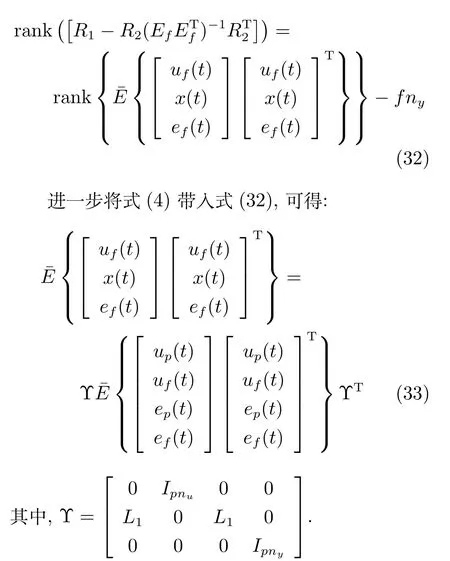
由于系统为可控可观测系统,采用文献[11]定理2可知Υ为满秩矩阵.同时如果式(33)第2项为正定满秩矩阵,根据文献[12]给定的秩条件可得:

因此,矩阵(32)为满秩矩阵.

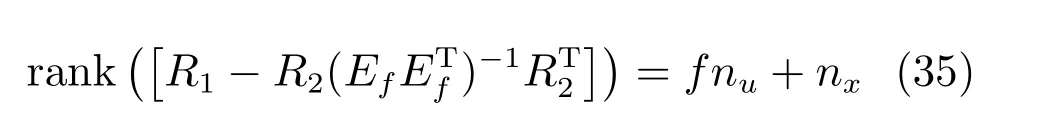
由式(30)、式(32)和式(35)可知

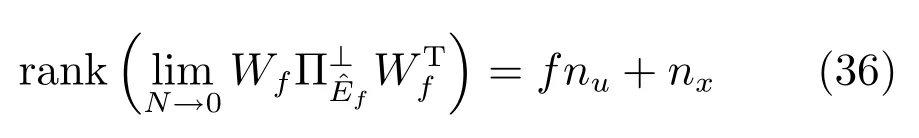
则

2.3 闭环一致条件合理性分析

第2.2节定理2的两个假设条件涉及未知新息信息,以上假设是否合理,将直接决定本文方法能否取得一致估计结果.

由于模型(1)可表示为模型(2),则新息的协方差可表示为(具体表述可参考文献[10]第5章),其中P为半正定矩阵,对于系统噪声有则可知

对于假设2,由于

进一步,由式(2)可知

其中,扩展可观性矩阵分别表示为L1=[Ap−1B ···AB B],L2=[Ap−1K···AK K],下三角形Toeplitz矩阵为

3 仿真研究

考虑文献[6]中研究的闭环系统

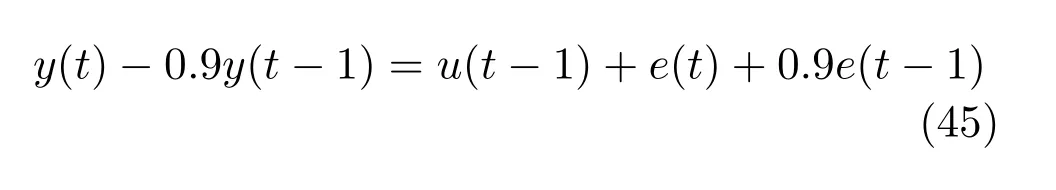
其中,反馈控制结构为u(t)=−0.6y(t)+r(t).过程噪声设置为方差为0.2的白噪声序列.

对系统设定输入激励r(k)为单位方差白噪声序列和相关序列两种情况进行研究.其中相关序列设为r(t)=(1+0.8q−1+0.6q−2)r0(t),r0(t)为单位方差白噪声序列.过去和未来水平数均设置为10.在不同数据长度N∈[200,8000]的情况下进行1000次Monte Carlo仿真.本文方法的辨识结果与SIMPCAwc算法[6]进行比较,当r(t)为单位方差白噪声系列时,系统极点(真实值为0.9)的估计平均值如图1所示,系统极点的估计标准方差如图2所示.当系统设定输入r(t)为相关系列时,系统极点的平均值如图3所示,系统极点的估计标准方差如图4所示.

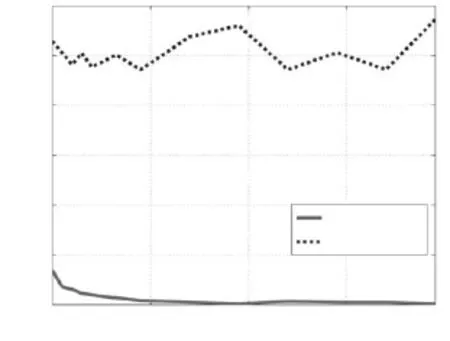
图1 系统设定输入激励为白噪声的系统极点估计平均值Fig.1 Mean value of estimated poles for white noise setpoint excitation

图2 系统设定输入激励为白噪声的系统极点估计标准方差Fig.2 Standard deviation of estimated poles for white noise setpoint excitation

图3 系统设定输入激励为相关序列的系统极点估计平均值Fig.3 Mean value of estimated poles for correlated quasi-stationary setpoint excitation

图4 系统设定输入激励为相关序列的系统极点估计标准方差Fig.4 Standard deviation of estimated poles for correlated quasi-stationary setpoint excitation

从以上结果可以看出,当系统设定输入为单位方差白噪声系列时,SIMPCAwc算法得出有偏估计结果;只有当系统设定输入激励为相关序列时,SIMPCAwc算法才能保证无偏估计结果.本文CSIMIEOP算法对系统设定输入激励为无关序列和相关序列时均可得到一致无偏结果,并且估计精度优于SIMPCAwc算法.

4 结论

本文提出一种基于新息估计和正交投影的闭环子空间辨识算法,对系统设定点输入激励为白噪声无关序列和相关序列的情况均可得到一致无偏估计结果,并且相对于近期有关文献给出的方法如SIMPCAwc算法[6],能进一步提高辨识精度.同时,严格分析和证明了本文算法保证一致估计的条件.最后通过仿真实例验证了本文方法的有效性和优越性.

1 Qin S J.An overview of subspace identification.Computers Chemical and Engineering,2006,30(10−12):1502−1513

2 Favoreel W,de Moor B,van Overschee P.Subspace state space system identification for industrial processes.Journal of Process Control,2000,10(2−3):149−155

3 Yang Hua,Li Shao-Yuan.Closed-loop subspace identification based on augmented input with consistency analysis. Acta Automatica Sinica,2007,33(7):703−708 (杨华,李少远.基于输入扩张的闭环系统子空间辨识及其强一致性分析.自动化学报,2007,33(7):703−708)

4 Wang Le-Yi,Zhao Wen-Xiao.System identification:new paradigms,challenges,and opportunities.Acta Automatica Sinica,2013,39(7):933−942 (王乐一,赵文九虎.系统辨识:新的模式、挑战及机遇.自动化学报, 2013,39(7):933−942)

5 van der Veen G J,van Wingerden J W,Bergamasco M, Lovera M,Verhaegen M.Closed-loop subspace identification methods:an overview.IET Control Theory and Applications,2013,7(10):1339−1358

6 Wang J,Qin S J.Closed-loop subspace identification using the parity space.Automatica,2006,42(2):315−320

7 Huang B,Ding S X,Qin S J.Closed-loop subspace identification:an orthogonal projection approach.Journal of Process Control,2005,15(1):53−66

8 Chiuso A.The role of vector autoregressive modeling in predictor-based subspace identification.Automatica,2007, 43(6):1034−1048

9 Qin S J,Ljung L.Closed-loop subspace identification with innovation estimation.In:Proceedings of the 13th IFAC System Identification.Rotterdam,Netherlands: IFAC, 2003.887−892

10 Katayama T.Subspace Methods for System Identification. London:Springer-Verlag,2005,107−137

11 Jansson M,Wahlberg B.On consistency of subspace methods for system identification.Automatica,1998,34(12): 1507−1519

12 Liu T,Huang B,Qin S J.Bias-eliminated subspace model identification under time-varying deterministic type load disturbance.Journal of Process Control,2015,25:41−49

13 Wang J,Qin S J.A new subspace identification approach based on principal component analysis.Journal of Process Control,2002,12(8):841−855

侯 杰 大连理工大学控制科学与工程学院博士研究生.主要研究方向为系统辨识. E-mail:jiehou.phd@hotmail.com

(HOU Jie Ph.D.candidate at the School of Control Science and Engineering,Dalian University of Technology.His main research interest is system identification.)

刘 涛 大连理工大学控制科学与工程学院教授.2012年入选国家青年千人计划,德国洪堡基金学者.主要研究方向为工业过程辨识建模,鲁棒过程控制,批量生产过程控制优化,过程质量监测.本文通信作者.E-mail:liurouter@ieee.org

(LIU Tao Professor at the School of Control Science and Engineering, Dalian University of Technology.He was a recipient of National Thousand Talents Program of China in 2012,and a Humboldt research fellow of Germany.His research interest covers industrial process identification and modeling, robust process control,batch process control and optimization,and process quality monitoring.Corresponding author of this paper.)

Closed-loop Subspace Model Identification Using Innovation Estimation and Orthogonal Projection

HOU Jie1LIU Tao1

In this paper,a closed-loop subspace model identification method using innovation estimation and orthogonal projection is proposed for closed-loop control systems.Firstly,a least-squares algorithm is adopted to estimate the innovation matrix via the vector autoregressive with exogenous inputs(VARX)model.Then,by performing an orthogonal projection of the observed input-output Hankel matrix onto the orthogonal complement space of innovation Hankel matrix to eliminate the influence from noise,the extended observability matrix and lower triangular block Toeplitz matrix are derived from the parity space of noise-free input-output data.Finally,the system matrices are retrieved by using a shiftinvariant approach.The consistent estimation conditions are analyzed with a strict proof.A simulation example is shown to demonstrate the effectiveness and merit of the proposed method.

Subspace identification,closed-loop identification,parity space,innovation estimation,orthogonal projection,consistent estimation

侯杰,刘涛.基于新息估计和正交投影的闭环子空间模型辨识.自动化学报,2016,42(11):1657−1663

Hou Jie,Liu Tao.Closed-loop subspace model identification using innovation estimation and orthogonal projection.Acta Automatica Sinica,2016,42(11):1657−1663

2016-01-19 录用日期2016-03-10

Manuscript received January 19,2016;accepted March 10,2016

国家自然科学基金(61473054),第三批国家青年千人计划,中央高校基本科研业务费重点培育基金(DUT15ZD108)资助

Supported by National Natural Science Foundation of China (61473054),National Thousand Talents Program of China,and Fundamental Research Funds for the Central Universities of China(DUT15ZD108)

本文责任编委方海涛

Recommended by Associate Editor FANG Hai-Tao

1.大连理工大学控制科学与工程学院大连116024

1.School of Control Science and Engineering,Dalian University of Technology,Dalian 116024

DOI 10.16383/j.aas.2016.c160050