SegHMC:一种基于Segmental HMM模型的顺式调控模块识别算法
2016-12-17郭海涛霍红卫于强
郭海涛 霍红卫 于强
SegHMC:一种基于Segmental HMM模型的顺式调控模块识别算法
郭海涛1霍红卫1于强1
顺式调控模块(Cis-regulatory module,CRM)在真核生物基因的转录调控中起着重要作用,识别顺式调控模块是当前计算生物学的一个重要课题.虽然当前有许多计算方法用于识别顺式调控模块,但识别准确率仍有待进一步提高.将顺式调控模块的多种特征信息结合在一起,有助于提高识别顺式调控模块的准确率.基于此,本文提出了一种识别顺式调控模块的算法SegHMC(Segmental HMM model for discovery of cis-regulatory module).该算法建立了一种关于顺式调控模块识别问题的Segmental HMM模型,进一步扩展了顺式调控模块调控结构(或调控语法)的表示,不仅将顺式调控模块表示为模体(Motif)的组合,还进一步将模体共同出现的频率、模体顺序偏好以及顺式调控模块中相邻模体间的距离分布等特征引入到顺式调控模块的调控语法中.在模拟数据集和真实生物数据集上的实验结果表明,本文方法识别顺式调控模块的准确率显著优于当前的主要方法.
基因的转录调控,模体,Segmental HMM,顺式调控模块识别
在基因的表达调控系统中,转录因子(Transcription factor,TF)通过与所调控基因附近被称为转录因子结合位点(Transcription factor binding site,TFBS)或模体(Motif)的特定DNA序列片段相结合,来启动基因的转录调控[1−2].在真核生物中,多个转录因子对基因的转录调控,并不是孤立进行的,而是转录因子之间或者各个转录因子与它们的模体之间通过一系列的时空交互来实施更复杂、更精确的转录调控.在被调控基因的调控区(Transcriptional regulatory region)中,模体非均匀地聚集为一系列的称为顺式调控模块(Cis-regulatory module,CRM)的离散区域,如启动子(Promoter)、增强子(Enhancer)、沉寂子(Silencer)、绝缘子(Insulator)等.结合这些顺式调控模块的转录因子通过相互协作、相互竞争,激活或抑制所调控基因的转录表达.一个顺式调控模块包含单个或多个转录因子的多个模体实例,其长度通常约为几百到几千个碱基对(Base pair,bp).一个真核生物基因调控区序列可能的调控结构的简单例子如图1所示.

图1 顺式调控模块结构示意图(顺式调控模块是包含多个转录因子相应模体的序列区;模体的方向、模体间的间隔距离、模体间的相互关系可能包含了给定顺式调控模块的重要性质.)Fig.1 The structure discription of cis-regulatory modules(A cis-regulatory module is a sequence region that contains multiple motifs of multiple transcription factors;motif orientation,the interval distance between motifs and their cooperation relationship may imply the important regulatory properties of the cis-regulatory module.)
识别顺式调控模块是理解基因转录调控分子机制的基础,同时也是构建基因调控网络[3−4]的关键步骤.此外,识别具有特定调控功能的顺式调控模块对疾病机理的研究也有重要的意义.许多疾病的发生都与基因的异常表达有关,调控基因表达的顺式调控模块发生变异是造成基因异常表达的主因.有证据表明特定顺式调控模块中协作调控元素的破坏,可以导致畸形和疾病;例如,Kleinjan等[5]发现PAX6的任何远端调控元素的缺失都会改变其表达水平,从而造成先天性眼球畸形、无虹膜以及大脑缺陷等疾病.
通过生物实验,例如高通量检测与顺式调控模块相关的表观遗传标记特征[6],可以识别顺式调控模块,但这种方法费时费力代价较大,并且许多时候受限于实验条件而很难实施.因此,使用计算方法直接从DNA序列中识别顺式调控模块已成为一个非常有吸引力的手段.
然而,使用计算方法识别顺式调控模块也存在着许多挑战:1)同一个顺式调控模块不同实例内的模体排列顺序并不完全相同,但也并非完全无序的.此外,模块内的模体之间的距离也不确定,即同一模块不同实例内相同的两相邻模体间的距离也都不相同.因此,很难确定性地刻画这种结构.2)真核生物的调控区通常很长,构成顺式调控模块的模体通常较短且存在退化,根据已知的模体或者借助于现有的模体库(如TRANSFAC[7]、JASPAR[8])直接搜索,会找出大量的假阳性匹配,所以很难通过直接搜索相关模体的方式来识别包含这些模体的顺式调控模块.
至今,已有多种用于识别顺式调控模块的模型和方法[6,9−27].为了识别真核生物基因的顺式调控模块,不同方法利用顺式调控模块的不同特征(如模体的聚集和物种间的保守性),使用不同搜索策略.
其中一类方法基于窗聚集,利用模体倾向于聚集的特性来搜索顺式调控模块.这类方法用最简单的方式表示顺式调控模块,通过概率统计度量给定长度窗口内的模体组合的统计显著性,相应方法如MSCAN[22]和MCAST[28]等,或者使用组合方法,在指定窗口大小范围内搜索在多个序列共同出现一组模体实例的最小区域,将其作为候选顺式调控模块,如CMStalker[29]等.这类方法本质上假定了序列窗内的模体之间独立同分布.这类方法虽然简单直接,但需要合理确定窗大小以及度量统计显著性的打分阈值,而这些参数在实际应用中通常很难确定;此外,这类方法也忽略了顺式调控模块可能的调控结构(或调控语法),如模体间的顺序和距离.
另一类方法基于概率模型,通过对序列或顺式调控模块建立概率模型,进而找出待搜索的目标序列中的顺式调控模块.基于概率模型的方法,除了少数采用判别模型的方法,如HexDiff[30]、Regulatory Potential[31]等外,大部分的方法使用生成模型,主要是隐马尔科夫模型(Hidder Markov model, HMM).HMM模型的主要优势在于,它可以对顺式调控模块的出现进行可靠的统计度量,并能刻画顺式调控模块的调控语法.此外,HMM模型所使用的期望最大化的参数估计算法,可以自动调节大量的参数,避免了手动设置的麻烦.基于HMM的顺式调控模块识别方法通常将顺式调控模块看作由一组过表达的模体和背景组合生成的序列片段.与窗聚集方法相比,它们不仅考虑了构成顺式调控模块的模体组合,也同时考虑了构成顺式调控模块的模体之间的距离.最初的一些方法,如CisModule[20],使用HMM间接捕捉顺式调控模块内部以及顺式调控模块之间背景的概率分布.但这种方法仅使用了一般的顺式调控模块内部背景,并未推断顺式调控模块内的模体之间的任何顺序.后续的方法,进一步扩展这种模型的表示,如Stubb[32]方法,创建了一个仅包含模体和背景两个状态的HMM模型,使用统计方法度量模体对间共同出现的显著性,进而决定是否引入相应的转移概率.通过使用定义在指定长度窗口内序列上的打分函数度量窗口内模体聚集显著性来预测顺式调控模块.该方法仅利用了HMM模型的转移概率,没有使用任何其他HMM模型特性.后来的方法CORECLUST[33]和TSHAS[14]建立了更复杂的HMM模型,引入了顺式调控模块内部背景状态,加入了模体到模体的概率转移,更细致地刻画了顺式调控模块的调控结构.训练和解码算法使用标准的Baum-Welch算法[34]和Veterbi算法[34].这类方法使用了HMM的特性,但局限于HMM的表达能力,建立的调控模型并不直观,添加了大量的辅助状态.另一类HMM相关的顺式调控模块识别方法,使用加强的HMM来刻画顺式调控模块的调控结构;如BayCis算法[35],使用贝叶斯层次HMM模型,对顺式调控模块和包含顺式调控模块调控序列进行建模.利用了层次HMM的特性建立了模体之间的概率转移.该模型将HMM状态转移参数看作随机变量,并引入贝叶斯先验.该模型虽然结构直观,表达能力强,但模型的训练和解码需要大量的计算.Lemnian等提出的基于Extended sunflower HMM的顺式调控模块识别方法[19],使用Extended sunflower HMM,对模型的刻画深入到模体内部,不仅刻画了模体间的依赖,还刻画了模体内部碱基之间的依赖关系,但该方法仅用于同型顺式调控模块的识别.
此外,还有一类方法利用相近物种的进化保守性来识别顺式调控模块,如 MorphMS[26]、MultiModule[36]和ReLA[27]等.这类方法首先通过双序列或多序列比对同源基因的调控区找出其中的保守区域,然后使用其他方法在保守区域中搜索顺式调控模块.由于大多数基因的调控区中存在着大量重复(Duplication)和改组(Shuffling)的序列片段,很难进行序列比对,所以这类方法并不总是有效.
将顺式调控模块的多种特征信息结合在一起,有助于提高识别顺式调控模块的准确率.顺式调控模块虽然结构具有不确定性,很难刻画,但作为频繁出现在多个被调控基因调控区中的调控功能单位,很可能包含某些保守成分.MOPAT[37]从一组同源基因的调控区中搜索保守模体模块(这里的保守模体模块被定义为在一组同源基因调控区中频繁出现且具有一定距离约束的相邻模体对,不考虑两个模体的相对顺序)出发,查找包含多个这种保守模体模块的区域,将其作为候选顺式调控模块,找出了一些保守的顺式调控模块.这一事实间接说明了顺式调控模块中存在保守成分.这里,我们同样利用保守模体模块这种顺式调控模块的保守成分,但限定保守模体模块内的模体具有特定的次序.然后,进一步将顺式调控模块保守性假设从同源基因(不同物种)推广到共调控基因(同一物种).最终,我们将顺式调控模块表示为由单模体和保守模体模块混合组成的,具有部分保守特征的调控结构(也称调控语法),从而将顺式调控模块结构保守性和其内部模体倾向于聚集的特征结合起来.为了刻画这种复杂的顺式调控模块调控结构,我们使用一种被称为Segmental HMM[38]的增强HMM模型来表达.
基于此,本文提出了一种识别顺式调控模块的概率模型方法SegHMC(Segmental HMM model for discovery of cis-regulatory module).该方法使用Segmental HMM在给定候选模体集上构建同源或共调控基因调控区序列和顺式调控模块的调控语法结构.同一般的识别顺式调控模块的HMM模型相比,我们不仅将顺式调控模块表示为模体的组合,还将模体共同出现的频率、模体顺序偏好以及顺式调控模块中的相邻模体之间距离分布等特征引入到顺式调控模块的调控语法当中,这些特征可以有效提高顺式调控模块的识别精度.此外,为了处理真核生物基因长的调控区,我们对模型进行了降低搜索空间的优化.这种优化通过提前进行片段分割,显式建立Segmental HMM状态转换图,去除了大量不必要的搜索路径,降低了搜索空间,同时又不失精度.得到的模型可用于待搜索目标基因调控区中甚至整个基因组中的相似顺式调控模块识别.我们分别在一个模拟数据集和两个真实生物数据集: Muscle数据集和果蝇早期发育数据集上对我们的方法进行测试,并选取当前主要方法进行比较,所有方法识别顺式调控模块的准确率使用通用评价指标相关系数(Correlation coefficient,CC)和F1-score来度量.实验结果表明,我们的方法识别顺式调控模块的准确率显著优于当前的主要方法.
1 SegHMC算法
1.1 SegHMC的Segmental HMM模型
Segmental HMM[38]是HMM的一个扩展,也称Generalized HMM.与一般HMM的每个状态仅能发射一个碱基相比,Segmental HMM的每个状态可以发射可变长度的碱基序列片段;状态所发射的碱基序列可由一个片段模型来表示.该片段模型,给出了生成长度为u的观察序列o=o1o2···ou的联合概率,可由下式表示.

因此,片段模型由两个分布组成,一个是描述片段长度似然的片段长度分布ds(u),另一个为表示不同长度观察序列发射概率的发射模型es(o).因此,在顺式调控模块的识别模型中,可以根据对顺式调控模块和调控序列结构的抽象,对这两个分布给出具体的定义.
本文使用Segmental HMM,在片段层次上对顺式调控模块和调控序列的调控结构进行建模,具有更强的表达能力;例如,可以对片段之间的依赖进行建模.本节将详细阐述Segmental HMM模型,该模型主要包括:模型的构建、状态转移概率、片段长度分布和生成状态的发射模型.
1.1.1 Segmental HMM模型构建
我们将转录调控序列的调控结构定义如下.转录调控序列由一系列的顺式调控模块和顺式调控模块之间的背景(称为全局背景)构成,而每个顺式调控模块又由一组具有特定次序的模体和模体之间的背景(称为局部背景)构成,这种抽象具有明显的层次性.基于这种结构定义,给定的转录调控序列可由下列过程生成:
1)定位给定候选模体集中的模体在目标转录调控序列中所有可能出现实例;
2)以这些被定位的模体实例为锚点,使用两模体实例之间的背景(全局背景或局部背景,具体类别待定)序列连接这些模体实例,从而生成整个调控序列.
上述过程中,我们允许模体实例在空间上存在重叠,模体之间可能通过多种类型的背景序列相连;因此,存在许多平行的生成路径.从这些路径中,找出最可能的生成路径,即可得出该转录调控序列最可能的调控结构,从而找出相应的顺式调控模块.
将每个具体片段(模体、全局背景和局部背景)表示为Segmental HMM的一个状态,片段之间的连接对应了两个状态之间的转移,根据上述生成过程,我们显式构造Segmental HMM的状态转换图.显式构建状态转换图一方面移除了不必要的状态路径,减小算法的搜索空间;另一方面,更便于构建模体的二元语法,模型顺式调控模块内的相邻模体间的一阶依赖关系.为了标识顺式调控模块,我们增加相应的辅助状态:顺式调控模块开始状态和顺式调控模块结束状态.图2给出了表示一个调控序列调控语法结构的Segmental HMM状态转换图的具体例子,整个模型所包含的状态如下:
2)模体状态M={m1,m2,···,mK};
4)顺式调控模块状态C,又由顺式调控模块开始状态Cs和顺式调控模块结束状态Ce构成,即C=Cs∪Ce=

Segmental HMM状态转换图的具体构造过程如算法1所示.
算法1.Segmental HMM状态转换图的构造
输入:一组Motif的PWM集PWMS,用于搜索Motif的p-value阈值和一个调控序列
输出:状态转换图的状态集Q和这些状态之间的连接集T
1)创建该模型的初始状态 S和终止状态 E
2)对PWMS中每个PWM,在所给调控序列中找出小于给定p-value阈值所有Motif匹配
3)根据找出的Motif匹配对所给调控序列进行分割,标记状态类型,创建相应的状态集M,Bg和Cs
5)以状态在序列中的位置为关键字对状态集Q进行排序
6)Ce←∅
7)Bc←∅
8)for每个状态qi∈Q do
9)if qi为模型的初始状态
10)从Q中顺序取出下一状态qi+1
11)T←T∪{qi→qi+1}
12)else if qi为一个全局背景状态then
13)从Q中找出qi位置之后的第一个全局背景状态,记为qj
14)T←T∪{qi→qj}
15)从Q中找出qi位置之后的第一个CRM初始状态,记为qj
16)T←T∪{qj→qi}
17)for qi的每个前端模体状态m do
18)创建一个CRM终止状态ce
19)Ce←Ce∪{ce}
20)T←T∪{m→ce}
21)T←T∪{ce→qi}
22)else if qi是一个CRM初始状态then
23)T←T∪{qi→mi}
24)else if qi是一个Motif状态then
25)从Q中找出qi位置之后且不与它重叠的下一Motif状态,记为qj
26)创建一个局部背景状态bc
27)Bc←Bc∪{bc}
28)T←T∪{qi→bc}
29)T←T∪{bc→qj}
30)Q←Q∪Ce∪Bc
31)以状态在序列中的位置为关键字对状态集Q进行重新排序
32)return Q和T
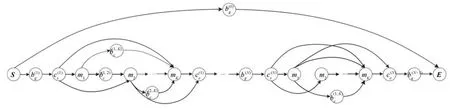
图2 Segmental HMM状态转移图Fig.2 The state transition diagram of segmental HMM
在我们的模型中使用位置权重矩阵(Position weight matrice,PWM)[39]表示相应的模体,在算法中提前给定待搜索顺式调控模块所包含的可能模体集,所对应的PWM集表示为PWMS.算法所要求的其他输入包括:搜索模体的p-value,以及待建模的转录调控序列.
在上述Segmental HMM状态转换图的构造算法中,第1行创建模型的初始状态和结束状态;第2行,根据所给p-value找出给定模体集中模体及其反向互补的模体在序列中所有的出现实例.第3行,根据所找出的模体实例,分别构建模体状态、全局背景状态和顺式调控模块开始状态,对应的状态集分别为M、Bg和Cs.第5行对所有状态的集合进行排序.第6~7行,分别初始化顺式调控模块结束状态集Ce和模体间局部背景状态集Bc.第8~31行,确定各状态间的转移,具体为:对于模型的初始状态(对应于第9~11行),只需连接下一任意有效状态;对于全局背景状态,需要与下一全局背景状态(对应于第13~14行)、相邻顺式调控模块初始状态(对应于第15~16行)和顺式调控模块终止状态(对应于第17~21行)相连;对于顺式调控模块初始状态,则只需连接到对应的模体状态,这对应于第22~23行;对于模体状态,对应于第24~29行,找出后续与当前状态不重叠的模体状态,然后创建相应的局部背景状态,并依次连接这些状态.第30~31行,将新创建的顺式调控模块结束状态和模体间局部背景状态加入到总状态集Q,并对Q重新排序.
关于上述构造算法的几点说明:
1)在第3行中,对每个模体,分别创建了位于模体前后的两个可能的全局背景状态.所创建的全局背景状态,仅有一端位置是确定的(即模体的前端或模体的后端),在后面第13~14行的操作中,会进一步将这些半连接的全局背景片段连接起来,形成一个大的全局背景;
2)在第5行和第31行中,按照两个关键字(位置、状态的类型)将前面分别生成的、无次序的各种状态按照生成转录调控序列的时空顺序进行排序,以便于后面确定各状态的连接转移的操作;
3)在算法中,我们显式地创建顺式调控模块的开始状态和结束状态,一方面,可以使结构更清晰,另一方面,也便于在推断时确定顺式调控模块的边界;
4)对于第27行,为了简化顺式调控模块的结构表示模型,我们假设顺式调控模块内相邻的模体间是非重叠的;
5)假定所给序列的长度为T,在整个算法中,耗时的操作主要集中在:模体的查找,最坏时间复杂度为O(KT),其中K为PWM的个数;查找后继状态的操作,最坏时间复杂度为O(T2);对状态集的排序,最坏时间复杂度为O(T2).因此,整个算法的时间复杂度为O(T2).
1.1.2 状态转移概率
在Segmental HMM状态转换图中,每个状态对应模体、全局背景或局部背景这些类型的一个实例,状态之间的转移概率即为相应状态类型之间转移的概率.
对于顺式调控模块内的模体状态mi和模体状态mj之间的转移概率,可由下式估计得到:

其中,t(m)表示模体状态(对应于模体实例)m所对应的模体类型,A为模体状态间的转移计数.
对于全局背景类型状态bg,其反映了在长的序列区域中出现顺式调控模块的概率.由状态bg到顺式调控模块状态的转移概率,或顺式调控模块到bg状态的转移概率,由于即使在很长的调控序列中顺式调控模块的数目也相对较少,所能获得的数据难以训练出可靠的模型参数.为避免过拟合,可由经验估计得出,作为常量参数,在系统运行时设定.
1.1.3 片段长度分布
全局背景长度和局部背景长度分别表示了顺式调控模块之间以及顺式调控模块内的模体之间的空白区域的长度分布.对于全局背景状态bg和局部背景状态bc,我们假定其序列长度分别满足期望为wg和wc的几何分布;这种假定一方面反映了我们对顺式调控模块结构的不确定性,另一方面又为模型顺式调控模块内的模体的二元语法特征提供足够的适应性.在该假设下,背景序列长度为d的概率为:
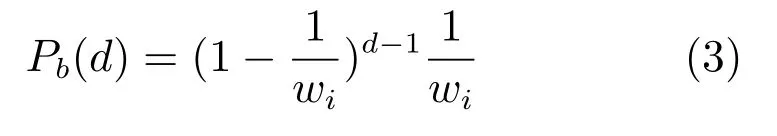
这里,b表示bg或bc,wi表示wg或wc.
对于模体状态m,由于模体所对应的位置权重矩阵[39]是直接从数据库中获取的,其长度wm及其特定位置碱基的概率都是已知的,所以模体状态上的序列长度d′的概率分布是特定的,即:
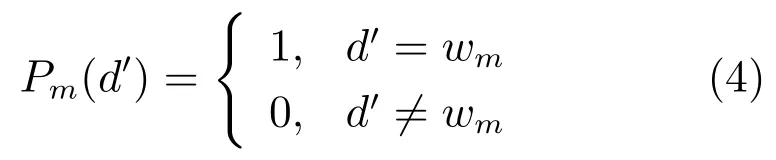
1.1.4 生成状态的发射模型
在本文模型中,只有模体状态、全局背景状态和局部背景状态为生成状态.每种生成状态发射长度满足特定分布的碱基序列片段.
对于全局背景和局部背景状态,我们分别使用k阶Markov模型和m阶的局部Markov模型.在局部Markov模型中,位置t处碱基的条件概率仅由以位置t为中心长度为2D的窗口内的序列片段来估计.这可采用记笔记的方式预先计算出每个位置碱基的条件概率,并存储计算的结果,需要时直接查表即得.
对于模体的生成概率,在本文模型中,使用经典的PM 模型[40].假定模体实例为O,该模体的PWM Θ=[θ1,θ2,···,θL],其中θi(1≤i≤L)为碱基频率的列向量,则模体状态所对应的碱基序列片段为O的概率为:
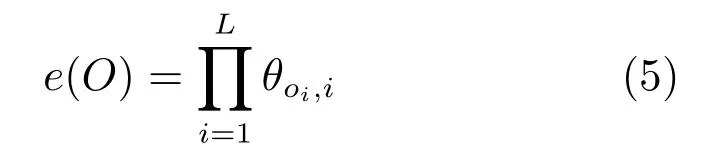
这里oi为模体实例O中第i位置的碱基.
1.2 解码和训练算法
在我们的模型中,将输入的序列分为训练集和测试集.在训练集上训练出模型参数后,使用已训练的模型识别给定测试集中所有序列的顺式调控模块,这一过程表现为解码出模型的最优状态路径过程.在Segmental HMM模型中,最优状态路径可形式化定义为:
给定长度为T的转录调控序列(即观测序列) O=o1o2···oT,设其对应的状态序列为Π=(π1,···,πT),则该转录调控序列所对应的最优状态序列可表示为:


这里 Psi(di)表示状态 si的序列片段长度的概率分布,asi,si+1为状态si到状态si+1的转移概率,e(oti+1···ti+1|si)表示状态si生成观测序列片段oti+1···ti+1的概率.
由于缺少足够的标注数据,本文模型使用无监督的Baum-Welch算法[34]直接从训练集中训练系统的模型参数.对于模型的初始状态概率,由于它只确定了输入序列的第一个位置的初始功能状态,在沿序列的后续操作中,其影响完全可以忽略,在本文模型中简单地由均匀分布随机生成.
我们已提前标出对应片段的可能状态,创建了Segmental HMM的状态转换图.因此,在解码时,不再需要通过使用像最大似然之类的方法去推断最可能的片段分割位置,可直接使用解码算法找出最优路径.为了求式(6)所对应的最优状态路径,本文使用基于动态规划的Veterbi算法[34],记为SegHMC Veterbi,并把它作为模型的缺省设置.此外,为了提供足够的弹性,代替求最优状态路径,本文还给出了类似于MAP(Maximum a posteriori probability)算法[34]基于阈值的后验解码算法,该算法给出了最可能的状态路径,记为SegHMC threshold.与MAP算法输出每个后验概率最大的序列区域相比,SegHMC threshold输出后验概率大于指定阈值包含顺式调控模块的序列区域.在SegHMC threshold算法中,本文搜索后验概率大于给定阈值且至少包含两个模体的连续区域作为候选顺式调控模块顺式调控模块.候选顺式调控模块区域的边界定义为首个模体的起始位置,和最后一个模体的结束位置.在本文模型中,选择的阈值范围为[0.45,0.70],在模型的后验推断中该范围内的阈值通常能给出好的性能.相对于完全输出后验概率最大的MAP输出来讲,能通过合理地选取相应的阈值在精度和召回率之间达到一个平衡.
1.3 SegHMC算法的整体框架
为了找出目标序列中的顺式调控模块,本文算法需要给定相应的输入,它主要包括:训练集、测试集、常量参数、候选模体的PWM集、筛选顺式调控模块的阈值.算法通过执行如下的过程,输出所有测试集中大于给定阈值的顺式调控模块:
1)在训练集上,使用第1.1.1节中的Segmental HMM构造算法构造相应的Segmental HMM模型,使用Baum-Welch算法训练出Segmental HMM的状态转移概率;
2)在测试集上,使用第1.1.1节中的Segmental HMM构造算法构造相应的Segmental HMM模型,利用第1)步训练得出的模型参数,使用Veterbi算法解码或基于阈值的后验解码算法找出最优或最可能的状态路径,预测出测试集中所有序列的顺式调控模块,进一步过滤得出大于给定阈值的顺式调控模块集.
模型的常量参数主要包括:搜索候选位点的pvalue;开始一个顺式调控模块的概率参数ps和结束一个顺式调控模块的概率参数pe;相邻位点距离的几何分布参数ml和相邻顺式调控模块距离的几何参数mg;以及顺式调控模块的权重阈值w.这些参数的取值首先结合真实生物数据特征的先验知识来选取;例如,一个序列中通常的顺式调控模块的含量、顺式调控模块的平均长度、顺式调控模块内模体间的平均距离等.其次,通过在模拟数据和搜集到的顺式调控模块数据集上,试验一个取值范围内不同的取值,选择在多数情况下能产生好的结果的值作为模型的参数.
算法所输出的顺式调控模块的具体信息主要包括:序列中所有找到的顺式调控模块的位置及其分值,以及构成顺式调控模块的模体、相应模体的位置和分值;其中,顺式调控模块分值和顺式调控模块内的各个模体的分值,分别标识了所找到的顺式调控模块和相应模体的统计显著性.我们将顺式调控模块的分值定义为对应的序列片段由顺式调控模块状态生成的后验概率和该序列片段由全局背景状态生成的后验概率的log似然比值;类似地,模体的分值定义为该模体所对应的序列片段由模体状态生成的后验概率和该序列片段由全局背景状态生成的后验概率的log似然比值.
2 实验结果分析
2.1 实验数据
我们在一个模拟数据集和两个真实生物数据集上测试本文方法:脊椎动物的Muscle特定表达系统和果蝇早期胚胎发育系统,以下简称Muscle数据集和果蝇早期发育数据集.这两个真实生物数据集是评价当前顺式调控模块方法性能的标准数据集[9−10],分别代表了两类不同的序列数据;其中Muscle数据上的序列为共调控序列,果蝇早期发育数据集中的序列为同源序列.
模拟数据集由30条序列和一个包含52个模体的模体集构成,这52个模体从TRANSFAC数据库中随机提取;其中,每个序列的长度均为20kbp.序列集中的每条序列包含0~3个顺式调控模块;这些顺式调控模块的长度随机为200~1500bp,模体位点间的空白的平均长度为50bp;每个顺式调控模块包含2~6种不同的模体,大约有15个模体位点实例;此外,为了模拟某些模体倾向于共同出现的偏好,设定每个顺式调控模块内包含40%的有序模体对;顺式调控模块内部和顺式调控模块间的背景序列均采用3阶Markov模型,模型参数通过扫描D.melanogaster基因组间的序列获得.
Muscle数据集最初由Wassermen和Fickett收集编录[41];后来,Klepper等选取该数据集的一个子集并进行了扩展,作为文献[9]中的基准数据.我们所使用的Muscle数据集即为文献[9]中的基准数据,该数据集共包含5个模体和来自不同物种24条共调控序列.所包含的模体具体为Mef2、Myf、Sp1、SRF和Tef,这些模体在肌肉的转录调控中起重要作用.所包含的24条序列,平均长度为850bp,分别来自老鼠、人类、鸡等物种.24条序列共包含5个模体的84个实例;每条序列均包含1个顺式调控模块,这些顺式调控模块的平均长度为120bp,其中最短的为14bp,最长的为294bp.
本文模型可以在一组具有相似调控结构基因的调控区上进行训练,然后用于搜索其他基因甚至整个基因组中的相似顺式调控模块.但限于收集完整标注全基因组数据的困难,我们仅在已标注的调控果蝇早期前后轴发育系统的一组基因上进行了测试.相较于Muscle数据集,果蝇早期发育数据集中的基因有相对较长的顺式调控模块.在该数据集中,我们选取参与果蝇早期胚胎发育转录调控的7个模体:Bcd、Hb、Cad、Kr、Kni、Tll和Gt,并从iDMMPWM数据库[42]中下载这些模体的PWM.我们从在果蝇早期胚胎发育过程中起重要作用的基因中选取一个包含7个基因的子集.这7个基因具体为:kni、kr、hb、tll、btd、eve和h,这些基因主要在果蝇早期胚胎的前后轴发育中调控果蝇幼体的体轴和体节发育.对于每个基因,我们选择D.melanogaster和其12个同源的对应基因序列作为搜索集.基因的染色体坐标和同源信息从FlyBase数据库[43]中获取.典型的真核生物基因的调控区的长度通常为包含转录起始位点上游15kbps和下游5kbps的区域,但为了尽可能地覆盖包含顺式调控模块的区域,我们将搜索区域定义为基因的转录起始位点附近的上游区20kbp和下游区20kbp,总共40kbp的序列区域,使用RepeatMasker软件(http://www.repeatmasker.org)掩住(即替换为N字符串)搜索区内的重复子序列.所选的7个模体和7个基因上的约91条序列构成了我们实验中所使用的果蝇早期发育数据集.我们从REDfly数据库[44]中收集这些基因的顺式调控模块,并对存在重叠的顺式调控模块进行合并,将整理后的集合作为真实注释的顺式调控模块基准集.
2.2 评价
为了对本文方法在上述数据集上的预测结果进行客观评价,并且使得评价结果不倾向于某一单个指标,我们使用评价指标相关系数(Correlation coefficient,CC)[45]和定义在精度(Precision)和召回率(Recall)上的F1-score[46]作为碱基水平上的主要评价指标对方法的预测准确率进行评价,这些指标被大多数顺式调控识别方法所使用.此外,为了评价本文方法在位点水平上的精度/召回率,我们画出了SegHMC threshold在不同阈值下的P/R曲线,以及模型缺省设置SegHMC Veterbi下的Precision/Recall值.这些评价指标的具体定义为:

这里TP、FP、TN和FN分别表示真阳性、假阳性、真阴性和假阴性;式(9)中的精度(Precision)和召回率(Recall)的具体定义为:
1)精度(Precison):Precision=TP/(TP+ FP),度量了预测的正确率,表示预测结果中被正确识别的顺式调控模块的比率;
2)召回率(Recall):Recall=TP/(TP+FN),度量了顺式调控模块的识别率,表示基准集中被正确识别的顺式调控模块的比率.
CC度量了预测集和基准集中碱基位置的相关性,同时考虑了预测结果的真阳性率和真阴性率. CC取值范围在–1和+1之间,+1表示预测结果与基准集完全一致,–1表示预测结果与基准集完全相反;当预测结果接近随机时,CC趋向于0.
从精度和召回率的定义,可以看到,它们分别衡量了预测算法的两个方面:查全率和查准率.虽然仅从定义上看这两个指标之间并没有必然的联系,但事实上它们在多数情况下是相互制约、相互矛盾的.这种制约和矛盾主要是由搜索策略的不完善造成的.通常情况下,如果希望获得较高的召回率,则不得不降低搜索策略标准,以尽可能地覆盖基准集中结果,从而引入了大量不相关的结果,降低了精度;如果想获得较高的精度,则需要提高搜索策略标准,这不可避免地过滤掉了相关的结果,造成了召回率的下降.因此,通常需要在这两个指标之间找到一个合理的平衡点.F1-score是精度和召回率的调和平均值,综合了方法的精度和召回率,度量了方法在精度和召回率之间达到平衡的能力;其值在0和1之间,值越高,通常表示算法的性能越好(在真阳性率方面).
我们使用 Cython 语言,将本文方法SegHMC开发成相应的工具,并在 Intel Xeon E5640@2.67GHz处理器,4GB内存的Windows 7 64位系统的平台上进行测试.
我们选取当前的主要方法:BayCis[35]、Stubb[32]、MSCAN[22]、MotEvo[25]、ReLA[27]和CMStalker[29],在 Muscle 数据集上与本文方法SegHMC进行预测性能的比较.
在这6个被比较的方法中,BayCis和Stubb属于概率模型方法,它们构造相应的HMM模型,训练模型参数,使用训练的HMM解码出给定序列中潜在的顺式调控模块.MSCAN是一个窗聚集方法,它计算给定序列滑动的窗内出现的所有模体聚集的统计显著性,将统计显著性超过给定阈值的序列区域判定为候选顺式调控模块.MotEvo是窗聚集和概率模型的结合,它使用贝叶斯模型对滑动窗口内的模体聚集区域进行打分,将分值大于给定阈值的区域作为候选顺式调控模块输出.CMStalker是一个组合方法,它综合了约束满足规划与参数松驰技术,能有效遍历模体组合的解空间,在给定的序列中找出可能的顺式调控模块.ReLA是一个基于局部比对的顺式调控模块搜索方法,它首先通过使用第三方模体搜索工具找出序列集中的所有模体,然后使用修改的Smith-Waterman算法,找出参考序列和被比较序列中得分最高的局部比对作为候选顺式调控模块.
2.3 模拟数据集上的结果
在模拟数据集上,模型固定参数具体设置为: ps=0.001,pe=0.1,p-value=0.01,和 w=100. mg和ml分别被设置为500bp和50bp,表示一个序列内的顺式调控模块间的平均距离为500bp,顺式调控模块内相邻模体间的平均距离为50bp.对于其他被比较的方法,我们使用其默认设置.
图3(a)给出了所有方法的CC值和F1-score值.从图中可以看出,我们的方法在这两个评价指标上明显优于其他方法.图3(b)给出了所有方法的P/R值.从图中可以看出,除MSCAN外的其他方法都有很高的召回率(Recall值),即所有方法的预测结果大都覆盖了所植入的顺式调控模块,但预测的精度(Precision值)表现出很大的差异.但我们方法的两个版本在保持高召回率的同时,精度超过绝大部分的其他方法,在精度和召回率之间达到一个很好的平衡.

图3 SegHMC threshold和SegHMC Veterbi在模拟数据集上的预测性能Fig.3 The prediction performances of SegHMC threshold and SegHMC Veterbi on the synthetic dataset
2.4 Muscle数据集上的结果
考虑到该数据集上的序列所包含的顺式调控模块,大多具有模体高度聚集但总体长度较短的特征,我们设置模型参数ml为20bp,同时保持其他参数值不变.
图4(a)给出了所有方法在Muscle数据集上的CC和F1-score值.从图中可以看出,本文方法SegHMC在这两个指标上均优于现存的方法(这里为模型缺省设置SegHMC Veterbi下的实验结果).
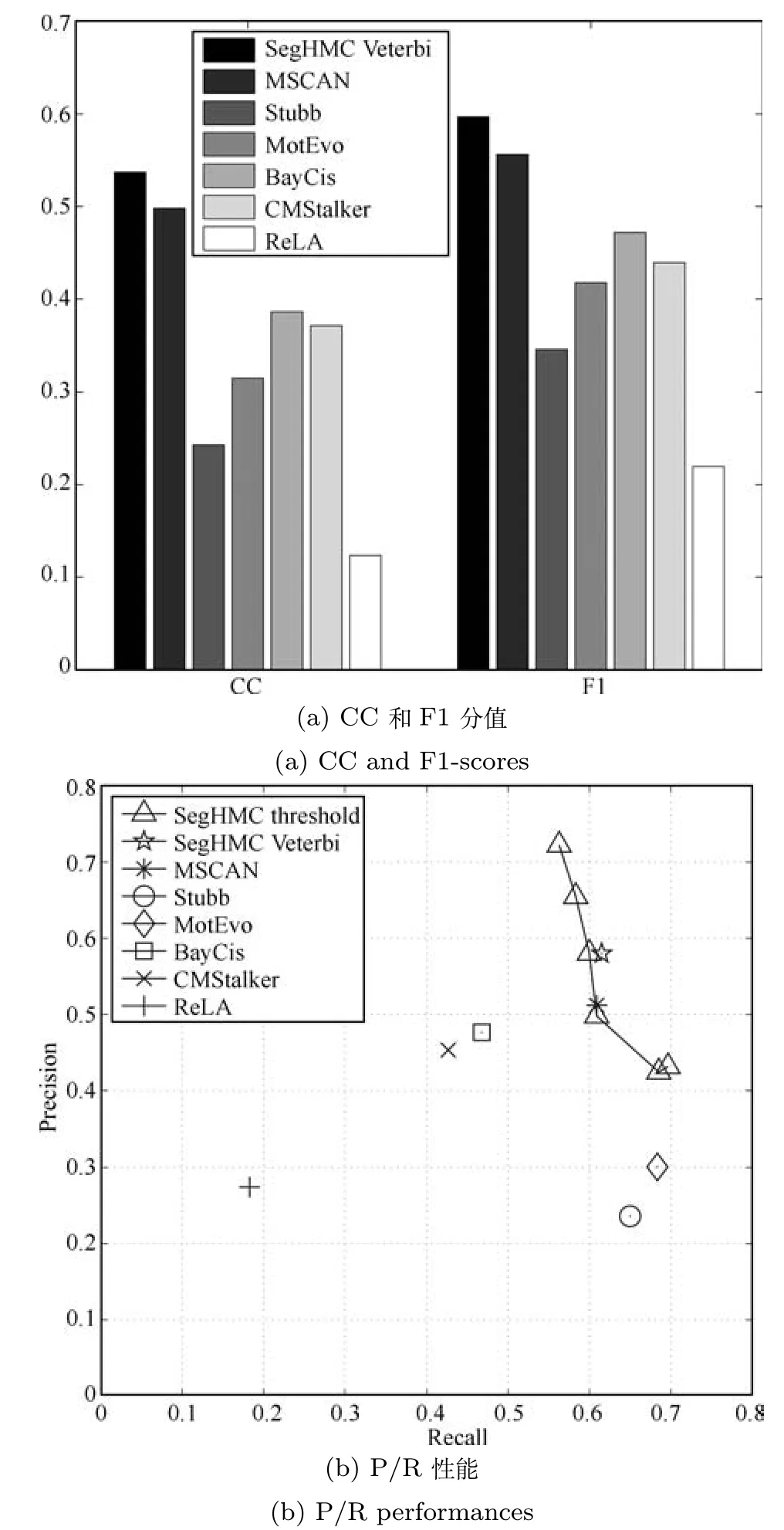
图4 SegHMC threshold和SegHMC Veterbi在Muscle集上的预测性能Fig.4 The prediction performances of SegHMC threshold and SegHMC Veterbi on the muscle dataset
为了考查SegHMC在该数据集上的具体表现,我们根据不同的阈值给出SegHMC threshold在位点水平上预测性能的P/R曲线.对于模型缺省设置SegHMC Veterbi和其他被比较的方法,我们根据它们的缺省输出在图中给出相应P/R值的点,如图4(b)所示.在图4(b)中,SegHMC threshold给出了一个平衡范围,SegHMC Veterbi输出位于曲线中间的一个点.
从图4(b)中可以看出,本文方法的两个版本在该数据集上较其他方法在预测精度和召回率之间均达到一个更好的平衡,具体为:在预测精度(Precision值)上高于其他大多数被比较的方法,召回率(Recall值)超过一半的方法.对于其他方法,分析图中的数据,还可以看到,在该数据集上不同的方法达到不同的P/R平衡,表现出不同的性能趋向.对于MotEvo和Stubb方法,它们倾向于给出较高召回率的预测,但整体上并未达到合理的平衡点,表现为预测精度(Precision值)明显低于所有方法的平均值,仅约为本文方法的一半.很显然,这种高的召回率是通过放宽顺式调控模块的筛选条件,尽可能覆盖可能存在顺式调控模块的序列区,以给出尽可能多的预测结果,牺牲预测精度换来的.而对于BayCis和CMStalker方法,为确保有较高的预测精度,它倾向于给出保守的预测结果,具体表现为其召回率(Recall值)明显低于其他方法.对于MSCAN方法,它并未完全倾向于某一单个指标,而是在保证召回率的同时,给出了较高的预测精度,表现出良好的预测性能.在所有的方法中,ReLA并不倾向任何单个指标,给出了最保守的预测.
2.5 果蝇早期发育数据集上的结果
我们将这些方法进一步在果蝇早期发育数据集上进行测试,模型的所有常量参数设置与模拟数据集上相同.其中,对于Stubb,我们选择其多物种版StubbMS(Stubb中的一个模块,在以下的描述中我们仍记为Stubb).StubbMS利用相近物种间的保守性来提高方法的预测性能,具体为:通过双序列比对,找出两物种间的保守区域,对保守区内的片段进行打分,将分值高于给定阈值的保守片段作为候选顺式调控模块.所有方法在该数据集上的整个测试方式如下:
1)对于 BayCis和 SegHMC,使用和D.melanogaster同源的所有其他果蝇物种的基因作为训练集,将D.melanogaster的对应基因作为测试集(REDfly数据库仅搜集了D.melanogaster基因的顺式调控模块标注信息,其他同源物种的顺式调控模块暂时无法搜集);
2)对于需要双序列比对的 Stubb方法,选取其原文中所使用的物种 (D.melanogaster和D.pseudoobscura),在相应基因上进行测试;
3)对于仅在单序列上预测顺式调控模块的方法MSCAN和MotEvo,仅在D.melanogaster相应的基因上进行测试;
4)对于ReLA,选取D.melanogaster相应的基因作为参考序列,其余同源基因序列作为被比对的序列;
5)对于CMStalker,在所有同源基因上进行测试.
图5(a)给出了所有方法在该数据集碱基水平上的CC和F1-score.从图中可以看出,与其他方法相比,本文方法SegHMC在整个数据集的CC和F1-score值(这里为模型缺省设置SegHMC Veterbi下的实验结果)上仍高于其他方法,表现出稳定的预测性能.此外,通过对比可以发现,与Muscle数据集上的结果相比,这些指标的分值均有较大幅度的下降.考查这两个数据集上数据的特征,发现这主要是由于搜索区长度的增加,而造成的信噪比(顺式调控模块相对于背景)的降低造成的.与Muscle数据集相比(序列平均长度为850bp),果蝇早期发育数据集中的序列更长(长度均为40kbp),各方法在识别单个模体时,不可避免地给出大量假阳性的预测,进而影响到顺式调控模块的预测结果,造成了预测结果中的大量假阳性预测.
图5(b)给出了所有方法位点水平上的P/R曲线.从图中可以看出,本文方法的两个版本都达到了很好的平衡.并且阈值方法在某些阈值上较缺省设置达到更好的平衡,尽管如此,我们也应该明白:在实际应用中,我们所能达到的平衡完全基于数据的输入,而P/R是完全未知的,我们很难选择合适的阈值参数,得到好的预测结果.因此,方法自动选择合适的参数达到适当的P/R平衡就显得更为重要.从图4(b)中,可以发现:在Muslce数据集上表现良好的MSCAN方法,在该数据集上表现得很差,其精度(Precision值)仅处于中间水平;召回率(Recall值)明显低于其他方法.在所有方法中MSCAN是唯一的基于窗聚集的方法,对于包含长度多变的顺式调控模块的序列,窗聚集方法很难确定一个合理的窗大小和打分阈值,从而给出好的预测结果(这里使用其默认输出);另一方面,MotEvo也是基于窗聚集的方法,但与纯粹的基于窗聚集的MSCAN方法相比,它结合了贝叶斯概率模型对滑动窗内的模体进行打分,从而有更好的性能,这也在某种程度上说明了,概率模型方法对不同类型的数据有更好的适应性.对于引入系统发生的方法Stubb和ReLA,通过序列比对利用物种的保守性确实提高了预测精度(具有仅次于本文方法的Precision值),但完全基于物种间的保守性很难保证有较高的召回率(其Recall值最低).虽然我们的方法未直接通过序列比对利用物种间的保守性,但通过概率模型刻画共调控或同源序列间结构的相似性,在某种程度上也利用了物种间的系统发生关系,这也是本文方法优于其他方法的一个原因.对于基于概率模型的方法BayCis,虽然在该数据集上给出了较高召回率(Recall值)的预测,但其预测的精度是最低的(Precision值).对于纯粹组合搜索方法CMStalker,给出了很保守的预测,与在Muscle数据集上的结果相比,预测精度和召回率都下降很多.考虑到该数据集上的顺式调控模块的长度特点,我们推测可能超出了CMStalker的所能处理的空间范围.
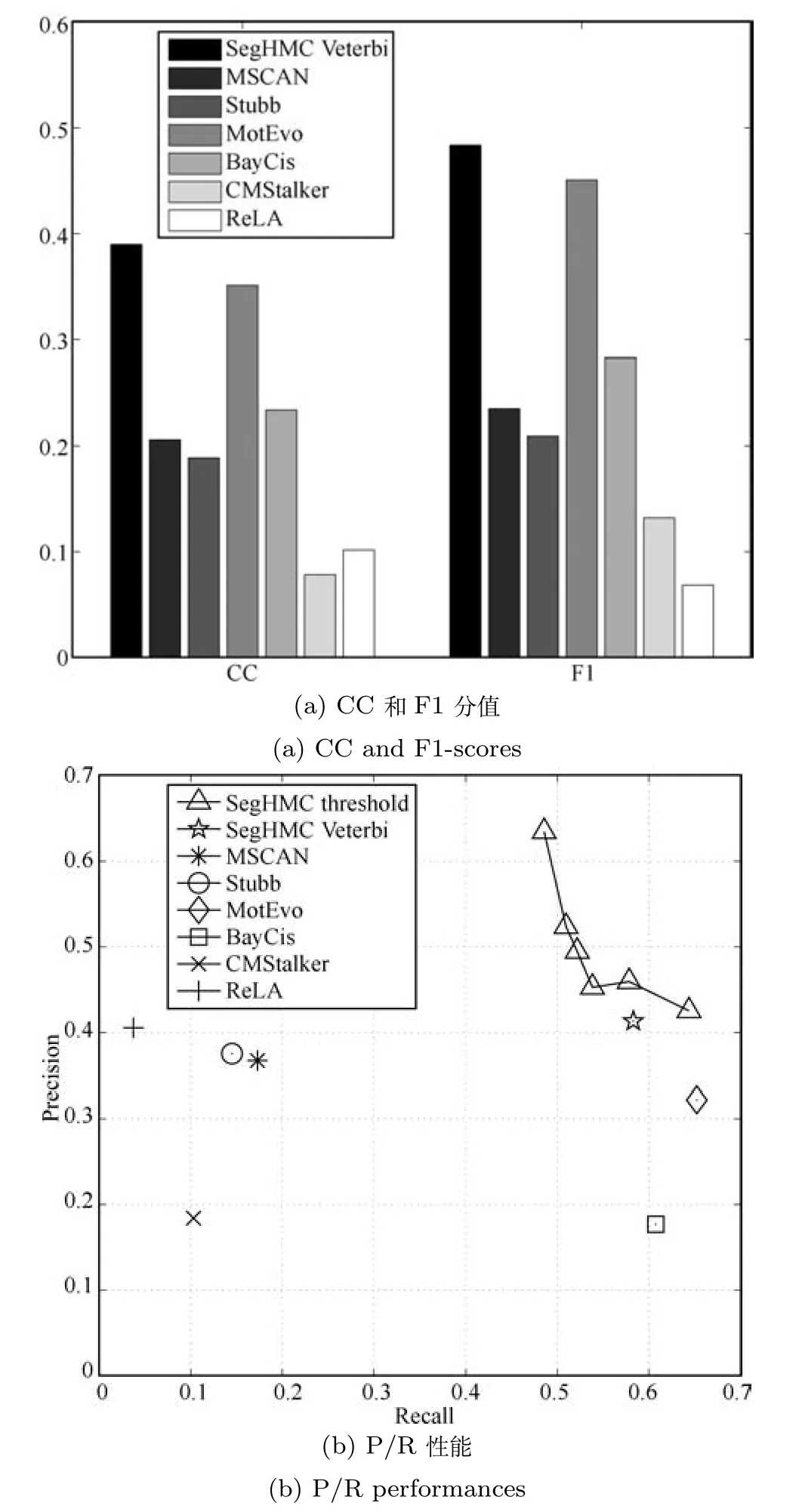
图5 SegHMC threshold和SegHMC Veterbi在果蝇早期发育数据集上的预测性能Fig.5 The prediction performances of SegHMC threshold and SegHMC Veterbi on the early drosophila development dataset
为了考查不同的方法在该数据集中单个数据上的预测性能的差异,我们画出了所有方法在该数据集中每个基因上的预测性能的箱线图,如图6所示.
图6给出了每个方法CC值的中位数、下四分位数和上四分位数以及最小值和最大值.从图中可以看出:所有方法在不同基因上的预测性能变化很大,这种变化要比方法总体性能之间的差异要大得多;这也说明了即使表现最好的方法在许多情况下也可能给出错误的预测.本文方法总体上较其他方法有更高的CC值,表现出更好的预测性能.虽然CMStalker在所有基因上的CC值变化最小,表现得最稳定,但其CC值总体上明显要低于大多数的方法.
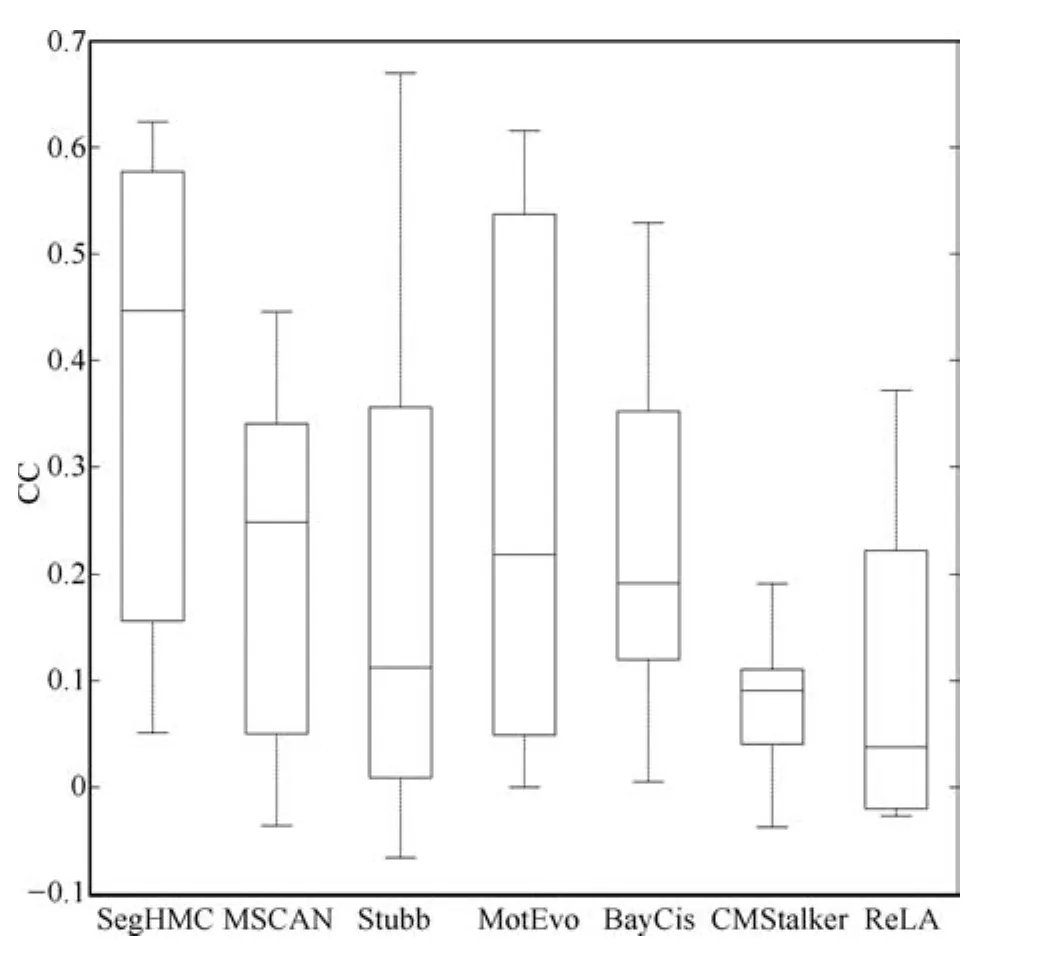
图6 所有方法在果蝇早期发育数据集中各基因上CC的变化Fig.6 A boxplot describing variation for all methods in CC across the genes in the early drosophila development dataset
2.6 引入的保守结构信息带来的性能提升
为了考查所引入的结构信息(相邻位点的相关性和位点间的距离分布)对方法性能的影响,我们回退模型到不考虑这些结构信息一般模型,记为SegHMC-simple,在所有3个数据集上进行实验对比,如图7所示.
从图中可以看出,加入结构信息的模型SegHMC相对未加入相关信息的SegHMC-simple总体上具有明显的性能提升,尽管对于不同的数据集性能提升不同.总体上,SegHMC在模拟数据和Muscle数据集上,较果蝇早期发育数据集上的提升要大.我们推测可能的原因在于,果蝇早期发育数据集上较大的搜索空间中所存在的大量噪声造成的,即结构信息的引入,可能增强原本的弱信号,引入了假阳性,抵消了一部分结构信息所带来的性能提升.检查SegHMC在3个数据集上所找到的顺式调控模块,可以发现,SegHMC能找出模拟数据集中所植入的70%以上共现模体对;在Muscle数据集中,找出了Mef2-Myf[7]、Myf-Sp1[7]以及Tef-Mef2[47]等经过生物实验验证的模体对;在果蝇早期发育数据集上找出了共现的同型模体对[48],如Bcd-Bcd、Kr-Kr以及Hb-Hb等.
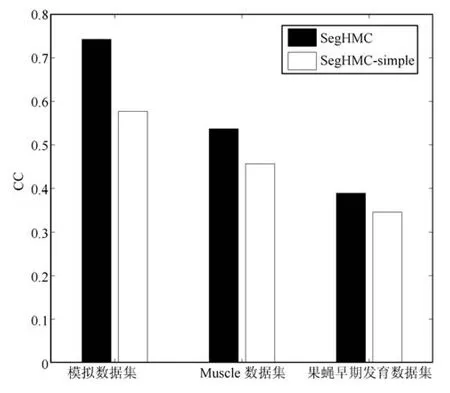
图7 引入结构信息后SegHMC在所有数据集上性能的提升Fig.7 An effect of inclusion of structural information on the prediction performance of SegHMC for all datasets
3 结论
本文将顺式调控模块的模体聚集特征和内部结构保守性结合起来,抽象出一种复杂的顺式调控模块的调控结构表示(或称调控语法),并借助于具有更强表达能力的Segmental HMM来表达,建立了一种识别顺式调控模块的概率模型.与其他基于概率类型的顺式调控模块识别方法相比,本文方法有如下的优点:
1)我们不仅将顺式调控模块表示为模体的组合,还将模体共同出现的频率、模体顺序偏好以及顺式调控模块中的相邻模体之间距离分布等特征引入到顺式调控模块的调控语法表示当中,这些特征可以有效提高顺式调控模块的识别精度.
2)Segmental HMM的状态可以表示一个序列片段,这一特性使得我们可以将所抽象的顺式调控模块的结构元素(模体、背景等)直接映射为Segmental HMM的一个状态.在模体而不是碱基的抽象层次上对顺式调控模块的调控结构进行建模,从而使得整个模型结构的表示更清晰、更自然.此外,Segmental HMM并不限定片段长度的具体分布,使得我们可以根据模型假定选取特定的片段长度分布.
3)通过预先搜索模体实例,提前标定相应片段的类型,显式构建Segmental HMM的状态转换图,有效减少了待搜索空间,提高了算法效率,使得本文方法可以处理真核生物普遍的长调控区序列.此外, segmental HMM模型所固有的在线(Online)性质,使得本文模型可以经过在一组具有相似调控结构基因的调控区上进行训练,然后用于搜索其他所要研究基因甚至整个基因组中的相似顺式调控模块.
为进一步提高识别顺式调控模块的性能,我们在后续的研究中打算从以下几个方面着手,以进一步完善我们的工作:一方面,我们将搜集更多标注的顺式调控模块,并使用更系统的方法,比如交叉验证,来辅助模型参数的选择.我们相信这些措施能使我们方法的性能得到进一步的提升.另一方面,当前新的生物测序技术,如染色质共沉淀后微阵列分析(Chip-chip)或染色质共沉淀后测序(Chip-seq)等的快速发展,产生了DNA双螺旋结构Profile、染色质结构、组蛋白修饰、蛋白质占位等的大量实验数据,这些数据隐藏着基因表达调控规律,进一步分析提取这些可用于顺式调控模块预测的生物信息,并将这些信息与现有的计算模型结合,构建更有效的顺式调控模块识别方法也是我们今后进一步努力的方向.
1 Wasserman W W,Sandelin A.Applied bioinformatics for the identification of regulatory elements.Nature Reviews Genetics,2004,5(4):276−287
2 Davidson E H.The Regulatory Genome:Gene Regulatory Networks in Development and Evolution.San Diego,California:Academic Press/Elsevier,2006.
3 Wang Pei,Lv Jin-Hu.Control of genetic regulatory networks: opportunities and challenges.Acta Automatica Sinica,2013,39(12):1969−1979 (王沛,吕金虎.基因调控网络的控制:机遇与挑战.自动化学报, 2013,39(12):1969−1979)
4 Chen L N,Wang R S,Zhang X S.Biomolecular Networks: Methods and Applications in Systems Biology.Hoboken, New Jersey:Wiley,2009.
5 Kleinjan D A,Seawright A,Mella S,Carr C B,Tyas D A,Simpson T I,Mason J O,Price D J,van Heyningen V. Long-range downstream enhancers are essential for Pax6 expression.Developmental Biology,2006,299(2):563−581
6 Hardison R C,Taylor J.Genomic approaches towards finding cis-regulatory modules in animals.Nature Reviews Genetics,2012,13(7):469−483
7 Matys V,Kel-Margoulis O V,Fricke E,Liebich I,Land S,Barre-Dirrie A,Reuter I,Chekmenev D,Krull M,Hornischer K,Voss N,Stegmaier P,Lewicki-Potapov B,Saxel H,Kel A E,Wingender E.TRANSFAC®and its module TRANSCompel®:transcriptional gene regulation in eukaryotes.Nucleic Acids Research,2006,34(Database issue): D108−D110
8 Portales-Casamar E,Thongjuea S,Kwon A T,Arenillas D,Zhao X,Valen E,Yusuf D,Lenhard B,WassermanWW,Sandelin A.JASPAR 2010:the greatly expanded open-access database of transcription factor binding profiles.Nucleic Acids Research,2010,38(Database issue): D105−D110
9 Klepper K,Sandve G K,Abul O,Johansen J,Drablos F.Assessment of composite motif discovery methods.BMC Bioinformatics,2008,9:123
10 Su J,Teichmann S A,Down T A.Assessing computational methods of cis-regulatory module prediction.PLoS Computational Biology,2010,6(12):e1001020
12 Suryamohan K,Halfon M S.Identifying transcriptional cisregulatory modules in animal genomes.Wiley Interdisciplinary Reviews:Developmental Biology,2015,4(2):59−84
13 Thompson J A,Congdon C B.GAMI-CRM:using de novo motif inference to detect cis-regulatory modules.In:Proceedings of the 2014 IEEE Congress on Evolutionary Computation.Beijing,China:IEEE,2014.1022−1029
14 Zheng Shu-Rui.Research of Cis-regulatory Module Discovery Method Based on HMM Model[Master dissertation], Xidian University,China,2012 (郑树锐.基于HMM模型的顺式调控模块识别方法的研究[硕士学位论文],西安电子科技大学,中国,2012)
15 Navarro C,Lopez F J,Cano C,Garcia-Alcalde F,Blanco A.CisMiner:genome-wide in-silico cis-regulatory module prediction by fuzzy itemset mining.PLoS One,2014,9(9): e108065
16 Rouault H,Santolini M,Schweisguth F,Hakim V.Imogene:identification of motifs and cis-regulatory modules underlying gene co-regulation.Nucleic Acids Research,2014, 42(10):6128−6145
17 Potier D,Seyres D,Guichard C,Iche-Torres M,Aerts S, Herrmann C,Perrin L.Identification of cis-regulatory modules encoding temporal dynamics during development.BMC Genomics,2014,15(1):534
18 Thompson J A,Congdon C B.Initial results in using de novo motif inference to detect cis-regulatory modules.In: Proceedings of the 2013 International Conference on Bioinformatics,Computational Biology and Biomedical Informatics.Washington DC,USA:ACM,2013.687
19 Lemnian I M,Eggeling R,Grosse I.Extended sunflower hidden Markov models for the recognition of homotypic cisregulatory modules.In:Proceedings of the 2013 German Conference on Bioinformatics.Gottingen,Germany,2013. 101−109
20 Zhou Q,Wong W H.CisModule:de novo discovery of cisregulatory modules by hierarchical mixture modeling.Proceedings of the National Academy of Sciences of the United States of America,2004,101(33):12114−12119
21 Gan Y L,Guan J H,Zhou S G,Zhang W X.Identifying cisregulatory elements and modules using conditional random fields.IEEE/ACM Transactions on Computational Biology and Bioinformatics,2014,11(1):73−82
22 Alkema W B,Johansson O,Lagergren J,Wasserman W W. MSCAN:identification of functional clusters of transcription factor binding sites.Nucleic Acids Research,2004,32(Web Server issue):W195−W198
23 Aerts S,Van Loo P,Thijs G,Moreau Y,De Moor B.Computational detection of cis-regulatory modules.Bioinformatics, 2003,19(Suppl 2):ii5−ii14
24 Sharan R,Ovcharenko I,Ben-Hur A,Karp R M.CREME:a framework for identifying cis-regulatory modules in humanmouse conserved segments.Bioinformatics,2003,19(Suppl 1):i283−i291
25 Arnold P,Erb I,Pachkov M,Molina N,van Nimwegen E. MotEvo:integrated Bayesian probabilistic methods for inferring regulatory sites and motifs on multiple alignments of DNA sequences.Bioinformatics,2012,28(4):487−494
26 Sinha S,He X.MORPH:probabilistic alignment combined with hidden Markov models of cis-regulatory modules.PLoS Computational Biology,2007,3(11):e216
28 Bailey T L,Noble W S.Searching for statistically significant regulatory modules.Bioinformatics,2003,19(Suppl 2):ii16−ii25
29 Leoncini M,Montangero M,Pellegrini M,Tillan K P.CMStalker:a combinatorial tool for composite motif discovery. IEEE/ACM Transactions on Computational Biology and Bioinformatics,2015,12(5):1123−1136
30 Chan B Y,Kibler D.Using hexamers to predict cisregulatory motifs in Drosophila.BMC Bioinformatics,2005, 6:262
31 Kolbe D,Taylor J,Elnitski L,Eswara P,Li J,Miller W, Hardison R,Chiaromonte F.Regulatory potential scores from genome-wide three-way alignments of human,mouse, and rat.Genome Research,2004,14(4):700−707
32 Sinha S,van Nimwegen E,Siggia E D.A probabilistic method to detect regulatory modules.Bioinformatics,2003, 19(Suppl 1):i292−i301
33 Nikulova A A,Favorov A V,Sutormin R A,Makeev V J, Mironov A A.CORECLUST:identification of the conserved CRM grammar together with prediction of gene regulation. Nucleic Acids Research,2012,40(12):e93
34 Durbin R,Eddy S R,Krogh A,Mitchison G.Biological Sequence Analysis:Probabilistic Models of Proteins and Nucleic Acids.Cambridge:Cambridge University Press,1998.
35 Lin T H,Ray P,Sandve G K,Uguroglu S,Xing E P.Bay-Cis:a Bayesian hierarchical HMM for cis-regulatory module decoding in metazoan genomes.In:Proceedings of the 12th Annual International Conference on Research in Computational Molecular Biology.Singapore:Springer,2008.66−81
36 Zhou Q,Wong W H.Coupling hidden Markov models for the discovery of Cis-regulatory modules in multiple species. Annals of Applied Statistics,2007,1(1):36−65
37 Hu J F,Hu H Y,Li X M.MOPAT:a graph-based method to predict recurrent cis-regulatory modules from known motifs. Nucleic Acids Research,2008,36(13):4488−4497
38 Russell M J.A segmental HMM for speech pattern modelling.In:Processing of the 1993 IEEE International Conference on Acoustics,Speech,and Signal Processing.Minneapolis,MN,USA:IEEE,1993.499−502
39 Stormo G D.DNA binding sites:representation and discovery.Bioinformatics,2000,16(1):16−23
40 Liu X,Brutlag D L,Liu J S.BioProspector:discovering conserved DNA motifs in upstream regulatory regions of co-expressed genes.In:Proceedings of the 6th Pacific Symposium on Biocomputing.Hawaii,USA,2001.127−138
41 Wasserman W W,Fickett J W.Identification of regulatory regions which confer muscle-specific gene expression.Journal of Molecular Biology,1998,278(1):167−181
42 Kulakovskiy I V,Makeev V J.Discovery of DNA motifs recognized by transcription factors through integration of different experimental sources.Biophysics,2009,54(6): 667−674
43 Tweedie S,Ashburner M,Falls K,Leyland P,McQuilton P, Marygold S,Millburn G,Osumi-Sutherland D,Schroeder A,Seal R,Zhang H,The FlyBase Consortium.FlyBase: enhancing Drosophila Gene Ontology annotations.Nucleic Acids Research,2009,37(Database issue):D555−D559
44 Gallo S M,Gerrard D T,Miner D,Simich M,Des Soye B, Bergman C M,Halfon M S.REDfly v3.0:toward a comprehensive database of transcriptional regulatory elements in Drosophila.Nucleic Acids Research,2011,39(Database issue):D118-D123
45 Tompa M,Li N,Bailey T L,Church G M,De Moor B,Eskin E,Favorov A V,Frith M C,Fu Y T,Kent W J,Makeev V J,Mironov A A,Noble W S,Pavesi G,Pesole G,Rgnier M,Simonis N,Sinha S,Thijs G,van Helden J,Vandenbogaert M,Weng Z P,Workman C,Ye C,Zhu Z.Assessing computational tools for the discovery of transcription factor binding sites.Nature Biotechnology,2005,23:137−144
46 Shaw W M Jr,Burgin R,Howell P.Performance standards and evaluations in IR test collections:cluster-based retrieval models.Information Processing&Management, 1997,33(1):1−14
47 Maeda T,Gupta M P,Stewart A F R.TEF-1 and MEF2 transcription factors interact to regulate muscle-specific promoters.Biochemical and Biophysical Research Communications,2002,294(4):791−797
48 Lifanov A P,Makeev V J,Nazina A G,Papatsenko D A. Homotypic regulatory clusters in Drosophila.Genome Research,2003,13(4):579−588

郭海涛 西安电子科技大学计算机学院博士研究生.主要研究方向为生物信息学算法,并行算法.
E-mail:ght_311@sina.com
(GUO Hai-Tao Ph.D.candidate at the School of Computer Science and Technology,Xidian University.His research interest covers bioinformatics algorithms and pararllel algorithms.)

霍红卫 博士,西安电子科技大学计算机学院教授.主要研究方向为大数据算法与压缩数据结构,生物信息学算法,算法工程.本文通信作者.
E-mail:hwhuo@mail.xidian.edu.cn
(HUO Hong-Wei Ph.D.,professor at the School of Computer Science and Technology,Xidian University.Her research interest covers big data algorithms and compressed data structures,bioinformatics algorithms,algorithm engineering.Corresponding author of this paper.)

于 强 博士,西安电子科技大学计算机学院讲师.主要研究方向为生物信息学算法,并行算法.
E-mail:qyu@mail.xidian.edu.cn
(YU Qiang Ph.D.,lecturer at the School of Computer Science and Technology,Xidian University. His research interest covers bioinformatics algorithms and pararllel algorithms.)
SegHMC:an Algorithm for Discovery of Cis-regulatory Module Based on Segmental HMM
GUO Hai-Tao1HUO Hong-Wei1YU Qiang1
Cis-regulatory module(CRM)plays a key role in metazoan gene transcriptional regulation,and the discovery of cis-regulatory module has been a crucial research topic recently.Many computational methods have been proposed to predict the cis-regulatory module,but it is still a main task to further improve the prediction accuracy for cis-regulatory modules.Combining multiple features of cis-regulatory module together can improve the prediction accuracy for cisregulatory module.Based on this,the paper presents an algorithm SegHMC(Segmental HMM model for discovery of cis-regulatory module)for the discovery of cis-regulatory module based on segmental HMM.The model further extends the representation of the structure of cis-regulatory module(or regulatory grammar),which not only describes a CRM as a combination of a group of motifs but also further introduces the frequency of the occurrence of motifs,the favour of the order of motifs,and the distance distribution between the adjacent motifs and other features.Experiments on the benchmark datasets demonstrate that the proposed algorithm outperforms the present main algorithms in the prediction accuracy.
Gene transcriptional regulation,motif,segmental HMM,discovery of cis-regulatory module
郭海涛,霍红卫,于强.SegHMC:一种基于Segmental HMM模型的顺式调控模块识别算法.自动化学报,2016, 42(11):1718−1731
Guo Hai-Tao,Huo Hong-Wei,Yu Qiang.SegHMC:an algorithm for discovery of cis-regulatory module based on segmental HMM.Acta Automatica Sinica,2016,42(11):1718−1731
2015-05-18 录用日期2016-06-06
Manuscript received May 18,2015;accepted June 6,2016
国家自然科学基金(61173025,61373044,61502366),中国博士后科学基金(2015M582621)资助
Supported by National Natural Science Foundation of China (61173025,61373044,61502366),the Chinese Postdoctoral Science Foundation(2015M582621)
本文责任编委黄庆明
Recommended by Associate Editor HUANG Qing-Ming
1.西安电子科技大学计算机学院西安710071
1.School of Computer Science and Technology,Xidian University,Xi'an 710071
DOI 10.16383/j.aas.2016.c150309
