面向炼钢–连铸调度过程的两阶段优化模型与算法

王秀英 冯惠 任志考 周艳平

面向炼钢–连铸调度过程的两阶段优化模型与算法

王秀英1冯惠1任志考1周艳平1

以某钢厂多台转炉及多台精炼炉对多台连铸机的复杂生产线为研究对象,针对其调度过程涉及多设备、多目标、多约束等调度要素,且离散和连续变量混杂,采用常规建模方法难以满足现场对调度的精度及排产速度的需求问题,提出一种新型的两阶段优化建模方法.首先,证明了炉次从炼钢到连铸总等待时间最小的调度目标与该炉次在转炉开始作业时间最大是等价的事实,并以离散型的设备变量为决策变量,以转炉开始作业时间最大为动态规划最优指标,建立设备指派多阶段动态规划基本方程和设备指派优化模型;然后,以炉次在设备开始作业时间的连续型变量为决策变量,并将准时开浇的非线性调度指标转化成与之等价的线性优化目标,以在同一台连铸机上浇铸的炉次之间断浇的时间间隔最小、钢包在设备之间的冗余等待时间最小、提前与滞后理想开浇时间的时间间隔最小为目标,建立线性规划冲突解消模型.工业实验表明所提出两阶段优化建模方法在求解速度与求解精度均满足现场要求.

炼钢–连铸,生产调度,优化建模策略,设备指派模型,冲突解消模型

现代制造企业规模庞大、过程复杂等特征给制造过程的调度决策带来了极大的挑战[1].钢铁企业是最大的制造业之一,与其他制造业所不同的是钢铁企业生产过程是在高温、高能耗下进行的,工序之间的物流要求衔接紧密,在各工序的设备上要准时加工,以此来减少钢水的温降,降低能耗.这决定了钢铁行业比其他制造业的调度精度要求更高,调度速度要求快,调度难度会更大.

计算机技术的飞速发展给钢铁企业生产管理水平的提升带来了新的机遇.国内外大型钢铁企业于20世纪90年初将计算机技术与人工调度经验相结合建立调度管理系统[2−4],以此来提高调度的精度和生产效率.但所建立的调度系统是否好用、实用,关键看嵌入调度系统中的调度模型和方法是否符合钢厂工况实际.由于各个钢厂生产的产品不同,设备条件和工艺条件等也不完全相同,所建立的模型和采用方法也不同.所以,针对每个钢厂的具体生产设备条件及工艺过程,建立合理的调度模型及寻找有效的调度方法和优化技术是提高钢铁企业生产效率、降低生产成本的重要途径[5].

国外大部分钢厂都是针对自己钢厂生产设备条件和工艺特点建立了单目标或多目标调度模型[4,6].文献[6]以一个浇次总完成时间最小、每个炉次在工序之间的等待时间及作业完成时间总和最小为目标建立了混合规划模型,通过求解得到每个浇次的调度时间表.然后,在同一台连铸机上,按照浇次与浇次之间的时间间隔为60分钟对各浇次进行排序,从而得到所有浇次叠加后的生产调度表.由于文献[6]所述的所有浇次都在一台连铸机上浇铸且非连铸设备的作业时间均小于连铸作业时间,每个浇次又有60分钟的时间间隔,所以,在每个设备上无需考虑炉次间的设备冲突问题.生产工艺路径相对简单,所提出的模型难以应用到多台连铸机、多台转炉和精炼炉、多重精炼的复杂生产工艺情况.

近几年国内外学者们也开始对多台转炉、精炼炉对多台连铸机,多重精炼方式的调度问题进行了研究,并取得了一些成果[7−16].这些成果多数是先建立分段模型或混合整数规划模型,再采用经典优化方法(拉格朗日[7]、差分方法[8])、启发式方法[9−11]或智能优化方法(遗传算法[12]、蚁群[13−14]、果蝇[15]、蜂群[16]等)对模型进行求解,得到相应的调度结果.经典优化方法通常在求解精度上能达到现场满意的效果,但当规模超过45个炉次时,求解的速度难以满足现场要求.启发式方法能满足求解速度要求,但不能保证解的最优性.智能优化方法初始种群都是随机生成的,参数设置多数凭经验给出,没有理论依据,导致调度解的鲁棒性较差.所以,研究符合现场实际,在时间和解的精度上均能满足现场要求的实用调度方法具有重要的现实意义.

文献[17]通过对国内某大型钢厂多台转炉、多台精炼炉对多台连铸机的复杂生产过程的分析,建立了既含有设备变量(离散型变量)又含有时间变量(连续型变量),而且时间变量依赖于设备变量混合整数规划模型,分析了模型难以求解的原因.本文在文献[17]的基础上,提出了新的两阶段优化建模策略,解决了模型难以求解的问题,并在求解速度及求解精度上均满足现场的要求.

1 炼钢–连铸生产过程描述[18]

图1是某大型钢厂炼钢–连铸生产过程所使用的设备和生产工艺过程.首先,将高炉中的铁水注入铁水包且送到炼钢厂,并倒入转炉设备中进行吹炼,吹炼的过程是把高温条件下的铁水进一步冶炼为含碳量更低的钢水.然后,将转炉中的钢水倒入准备好的钢包中,由指定的台车和行车将装有钢水的钢包送到相应的精炼设备上进行精炼.精炼是将转炉冶炼的普通钢水继续进行脱碳、去硫和去除杂质等处理,使普通钢水变成优质钢水,以确保连铸机浇铸出合格的板坯.根据钢种的不同,有的钢水包需要经过一重精炼、两重精炼或三重精炼处理过程.所谓一重精炼是指钢水包只经过一次精炼处理,即只走一个精炼设备(例如:1#钢包走3#RH一个精炼设备);二重精炼是指钢水包需要经过两次精炼处理,即需要走两个精炼设备(例如:2#钢包走2#RH和KIP两个精炼设备);同理,三重精炼是钢水包需要经过三个精炼设备处理(3#钢包走1#RH、2#CAS和LF三个精炼设备).精炼处理结束后,再由指定的台车和行车将钢水包吊运到指定的连铸机前,并倒入对应的中间包中.中间包的钢水不断进入结晶器中,通过结晶振动冷却后,从连铸机拉出板坯.板坯经轧机(直轧/冷轧)轧成各种钢材产品以供销售.这是一个多台转炉、多台精炼炉对多台连铸机,具有不同精炼重数的炼钢–连铸生产工艺过程.

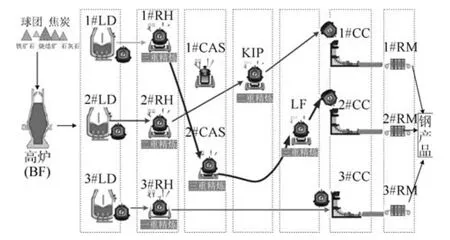
图1 炼钢–连铸生产工艺过程Fig.1 Production process of steelmaking-continuous casing

2 调度计划的两阶段优化建模策略

该大型钢厂炼钢–连铸生产调度计划的含义是以浇次计划为基础,在炉次的生产工艺路径,炉次在转炉、精炼炉上的加工时间、运输时间及各浇次开浇时间已知的条件下,确定各浇次中的炉次在哪台转炉、哪台精炼炉上加工,并确定出各炉次在转炉、精炼炉及连铸机上加工的开始时间和结束时间,形成炼钢–连铸生产作业时间表(称为调度计划),并确保浇次内的炉次连续浇铸,炉次在连铸前等待时间不能超过规定的时间,同一个设备两个相邻炉次不能产生作业冲突等目标[18].

2.1 变量及符号说明

i浇次序号,i=1,2,3,···,N;

Ni第i个浇次中的炉次数;

j炉次序号,j=1,2,···,Ni;

Lij第i个浇次的第j个炉次;

ϑij炉次Lij从转炉到连铸工序的加工设备总数;浇次计划中的精炼方式确定后, ϑij的取值就确定了;

θ炉次Lij从转炉到连铸加工的顺序号, θ=1,2,···,ϑij;

g表示设备类,g=1,2,3,···,G,如g=1表示转炉设备;g=2表示第一类精炼设备类,g=G表示连铸设备类;

Ti浇次i的理想开浇时间,由现场给定;

Mg表示第g类设备中含有的并行机数;

kg设备变量,表示g类设备的第k个设备序号;kg=1,2,3,···,Mg;

Tij(kg(θ)) 炉次Lij的第θ个操作在第g类设备的第kg(θ)个设备上的加工时间;当θ不同时,炉次Lij的操作设备类型g也不同,所以,g是θ的函数,即g=g(θ), kg=kg(θ);对于连铸设备,不同炉次在连铸机的处理时间是不尽相同的.所以,处理时间Tij(kg(θ))是设备变量kg(θ)的函数;

Tij(kg(θ), 炉次Lij从第θ个操作设备kg(θ)到第

kg(θ+1)) θ+1个操作设备kg(θ+1)之间的运输时间.由于炉次Lij的第θ和θ+1个操作设备不同,其运输时间也不尽相同,所以运输时间Tij(kg(θ),kg(θ+1))是炉次上下操作设备的函数;

yij(kg(θ)) 设备变量kg(θ)的函数,当yij(kg(θ))=1,表示炉次Lij的第θ个操作在g类设备上的第kg(θ)个设备上加工;否则, yij(kg(θ))=0;

xij(kg(θ)) 称为时间变量.炉次Lij的第θ个操作在第g类设备的第kg(θ)个机器上加工的开始时间.

1)性能指标

a)浇次准时开浇,即浇次中的第一个炉次偏离理想开浇时间尽可能小.

b)浇次内的炉次连铸浇铸,即同一个连铸机上相邻炉次断浇的时间最小.

c)炉次在不同设备之间的冗余等待时间尽可能的小.

2)约束条件

a)炉次操作顺序的约束,即炉次必须按其生产工艺路径进行加工.

b)同一设备不同炉次不能出现作业冲突约束.

c)炉次在连铸前最大等待时间不能超过企业规定的范围.

d)炉次在同类设备处理的唯一性约束.

e)按照现场给定的开浇时间准时开浇.

2.2 两阶段优化建模

2.2.1 基于动态规划的设备指派建模

1)设备指派建模分析

一个炉次从转炉炼钢到形成铸坯需要经过炼钢工序、多重精炼工序和连铸工序的生产过程.由于每道工序都可能存在并行机的问题,根据已知条件,除连铸阶段外,需要在具有并行机的工序上为炉次选取一个具体的加工设备.这是一个多阶段决策问题,动态规划是解决多阶段决策的最好方法.所以,本文基于动态规划方法建立设备指派模型.

使用动态规划方法的关键是根据实际问题建立多阶段决策的基本方程,为每个阶段做出决策.由于与炉次设备变量相关的调度性能指标为炉次从炼钢到连铸之间整个冗余时间最小.为建立动态规划的基本方程,需要将上述调度性能指标进行转化.

令wij表示任意一炉次Lij在其所有操作之间冗余时间之和,其最小值记为min wij.炉次在转炉开始加工时间最大,记为max{xij(k1)|k1=1,2, 3}.对于任意一个浇次中的任意一个炉次Lij,假设它从转炉到连铸工序所经过的设备数为ϑij,则Lij相邻两个操作θ与θ+1(θ=1,2,3,···,ϑij−1)设备间冗余时间为

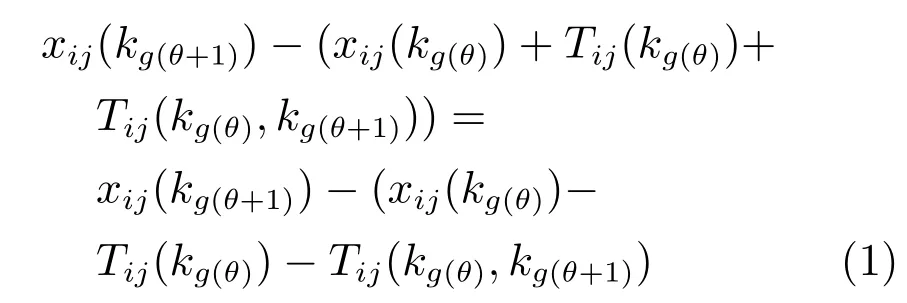
任意一个炉次Lij在其所有操作设备间冗余等待时间之和为

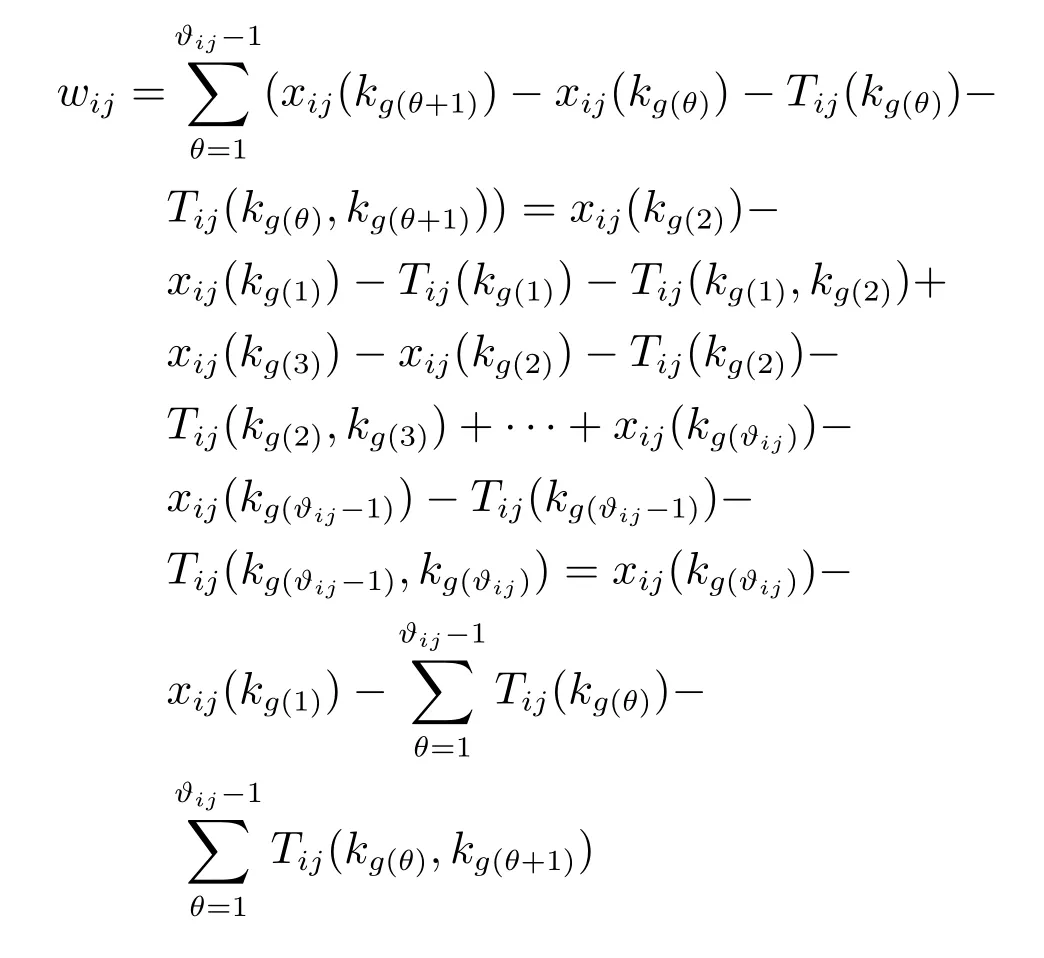
由于在连铸工位上有θ=ϑij,g(ϑij)=6;而在转炉工位上有θ=1,g(θ)=g(1)=1,则上式为

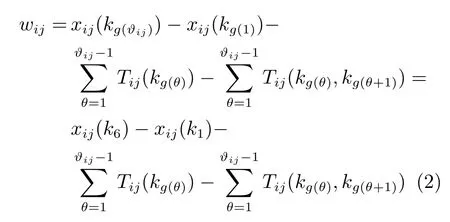
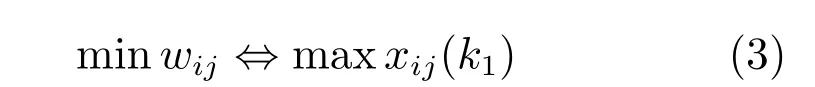
即一个炉次从炼钢到连铸总等待时间最小与该炉次在转炉开始作业时间最大是等价的.

2)设备指派动态规划的基本方程

令炉次在转炉的开始作业时间为xij(k1).根据炉次的生产工艺方式可知任意一个炉次的操作顺序θ=1,2,3,···,ϑij,依据动态规划各阶段状态转移方程可得:

从第一操作到第二操作状态转移方程为

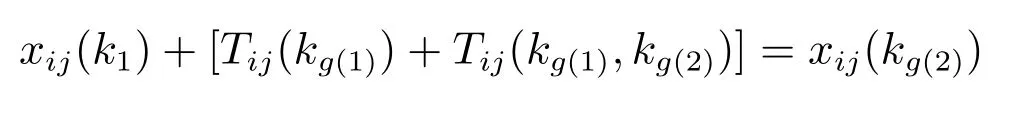
即

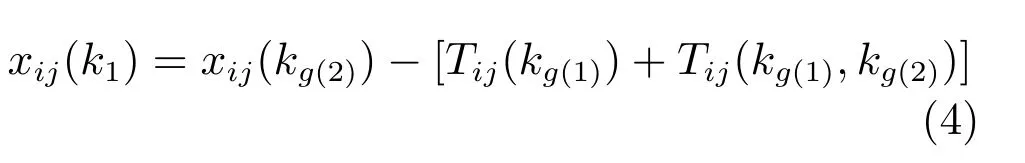
从第二操作到第三操作状态转移方程为

由此可得到从第θ个操作到第θ+1个操作状态转移方程为

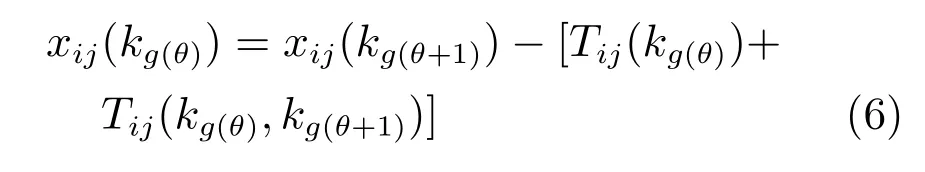
由于为炉次Lij指派设备时还需要考虑它在同设备上与已安排炉次Li'j'可能冲突的时间段,记为f(xij(kg(θ)),xi'j'(kg(θ'))).于是,从第θ个操作到第θ+1个操作状态转移方程应定义为

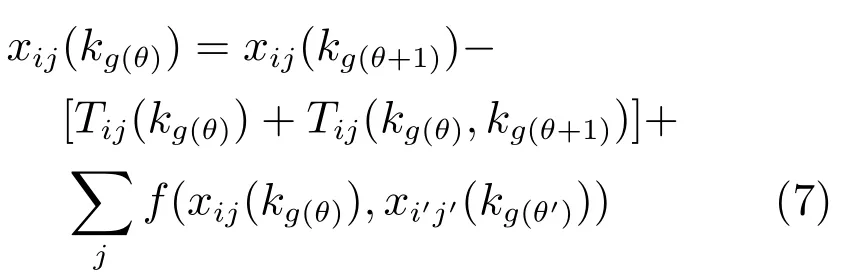
其中

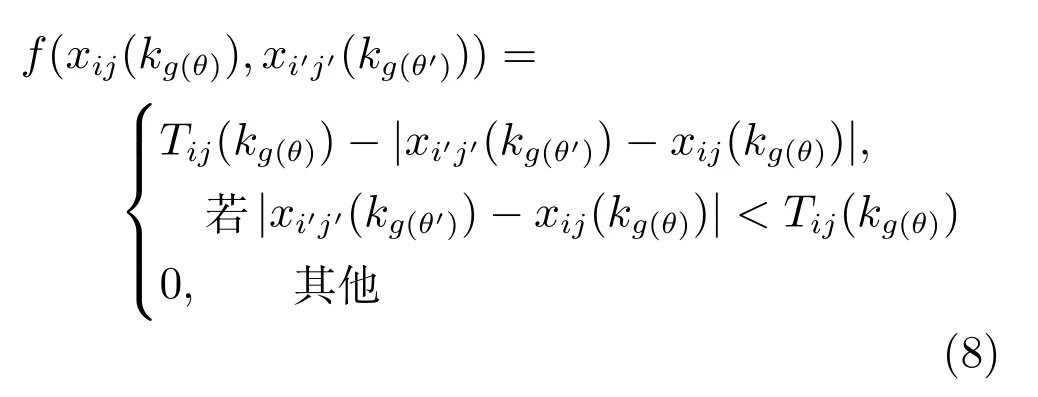
以各炉次Lij在连铸机上的开浇时间xij(k6)作为基本方程的初始条件,而xij(k6)是理想开浇时间Ti和炉次的浇铸时间Tij(k6)之和,于是有任意个炉次Lij从转炉到连铸各阶段(各操作)基本方程为

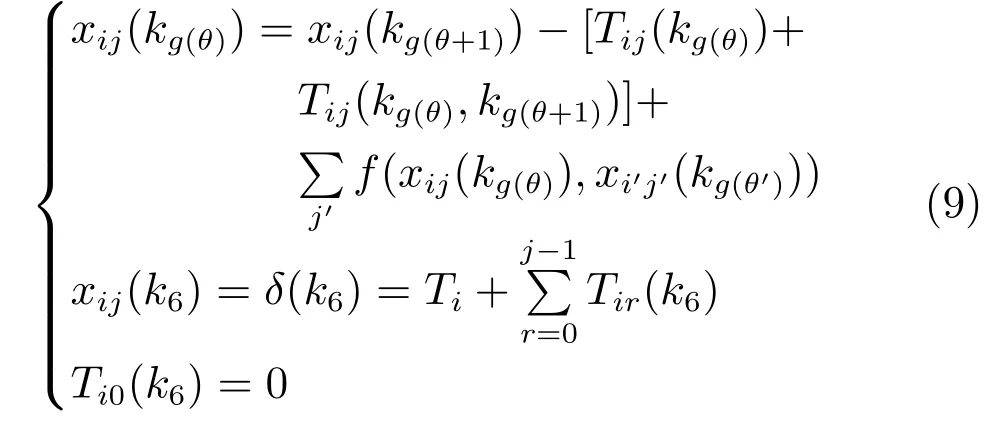
3)基于动态规划的设备指派模型

根据上面的分析,现以设备变量kg(θ)为决策变量,以炉次在转炉开始作业时间最大max{xij(k1)|k1=1,2,3}为最优指标函数,记为Fij(k1,k2,···,kϑij).以炉次在同类设备处理的唯一性为约束建立如下设备指派优化模型.

a)优化目标:

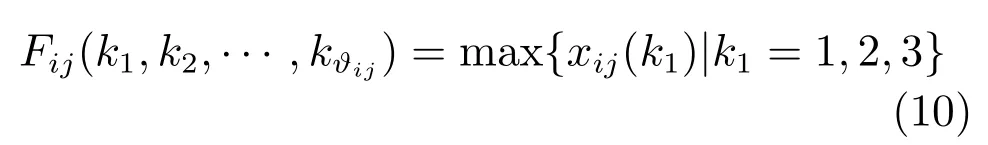
式中,xij(k1)可由状态转移方程(9)从连铸工序递推得到.

b)约束条件:

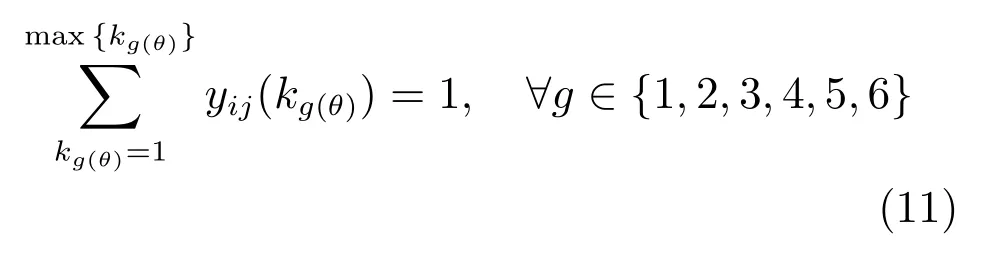
式中

2.2.2 冲突解消模型

设备指派模型的功能是依据炉次Lij的加工顺序θ=1,2,3,···,ϑij和动态规划基本方程(9)为炉次Lij确定出具体加工设备,记为但由于设备指派模型仅考虑了炉次Lij在所加工的设备之间的冗余等待时间最小的性能指标和选取设备唯一性约束,没有考虑调度的其他性能指标和约束,导致不同炉次在同一个设备上可能出现作业时间冲突现象.

冲突解消模型的功能是在Lij已确定了加工设备的基础上,重新确定炉次在其所加工设备上的开始作业时间和结束作业时间,以满足调度的各项指标和约束.

1)决策变量的选取

2)性能指标和约束条件

从文献[17]所建立模型的过程看,性能指标“浇次准时开浇”是一个非线性(含有绝对值)的目标函数.为提高求解速度,首先将非线性目标转换成两个线性目标,并给出两个变量的定义:

定义1.提前理想开浇时间的偏差量为

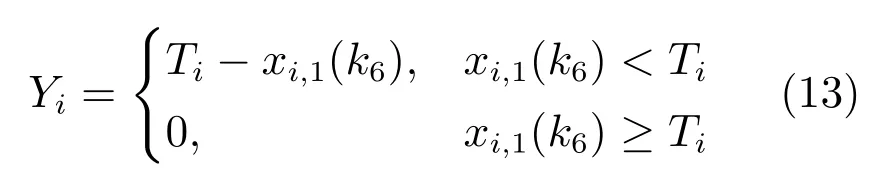
定义2.滞后理想开浇时间的偏差量为

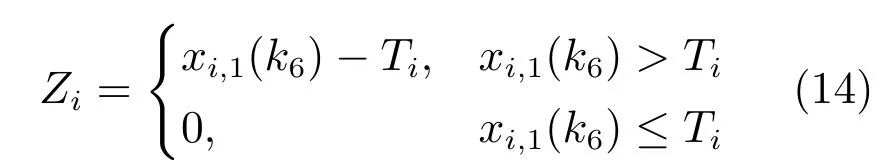
结论1.准时开浇的目标函数等价于提前与滞后理想开浇时间偏差量之和.

证明.由于

注1.结论1说明准时开浇的性能指标等价于浇次提前于理想开浇时间与滞后于理想开浇时间两个指标之和.在实际生产中这两个指标的重要程度是不一样的[19],因此,将准时开浇看成两个指标更符合实际.

3)基于线性规划的冲突解消模型

通过上述分析可知,建立冲突解消模型需要考虑如下4种性能指标:

a)浇次提前于理想开浇时间最小;

b)浇次滞后于理想开浇时间最小;

c)浇次内的炉次要连续浇铸;

d)浇次内各炉次在各操作设备上的冗余等待时间尽量小.

假设上述同类指标赋予相同的权重,则采用加权方法将多目标转化成单目标线性规划模型为

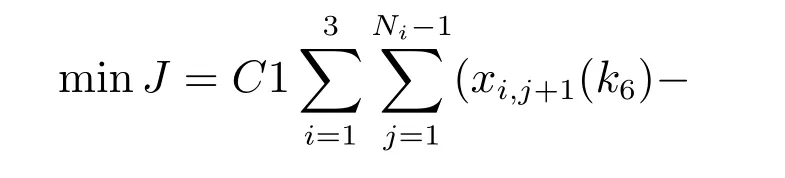
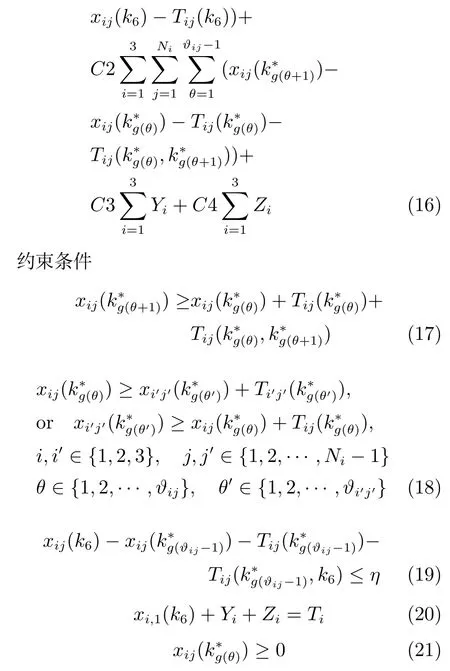
式(16)表示浇次内的炉次连续浇铸,炉次在设备间的冗余等待时间尽可能的小,提前于理想开浇时间和滞后理想开浇时间的时间间隔尽可能小的4个指标加权之和.其中,C1为连铸断浇惩罚系数; C2为炉次等待时间的惩罚系数;C3为前于理想开浇时刻的惩罚系数;C4为迟于理想开浇时刻的惩罚系数.式(17)对于同一炉次必须在前一个设备加工完成后方可在下一个设备上加工.式(18)同一设备上相邻两个炉次只有在前一炉次加工结束后方可进行下一炉次的加工.式(19)表示炉次在连铸前最大等待时间不能超过给定的阈值.式(20)表示准时开浇约束;式(21)表示决策变量非负性约束.

3 两阶段优化模型的求解步骤

3.1 第一阶段求解设备指派模型

1)求出各炉次在连铸机的浇铸时间(分钟),采用如下公式计算:

a)当该炉次为浇次的第一个炉,浇铸时间为

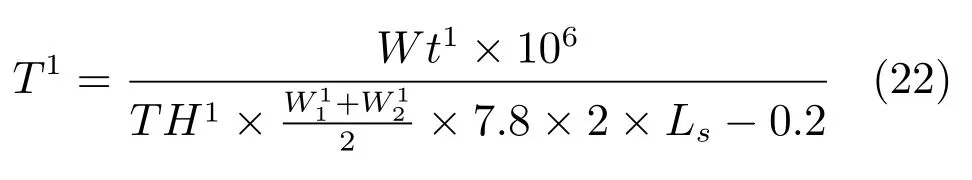
式中,Wt1为第一炉钢水的总重量(吨);TH1为浇铸钢水输出板坯的平均厚度(毫米);为浇铸钢水输出板坯的平均左、右宽度(毫米);Ls为连铸机的标准拉速(米/分钟).

b)当该炉次不是浇次第一个炉,浇铸时间为

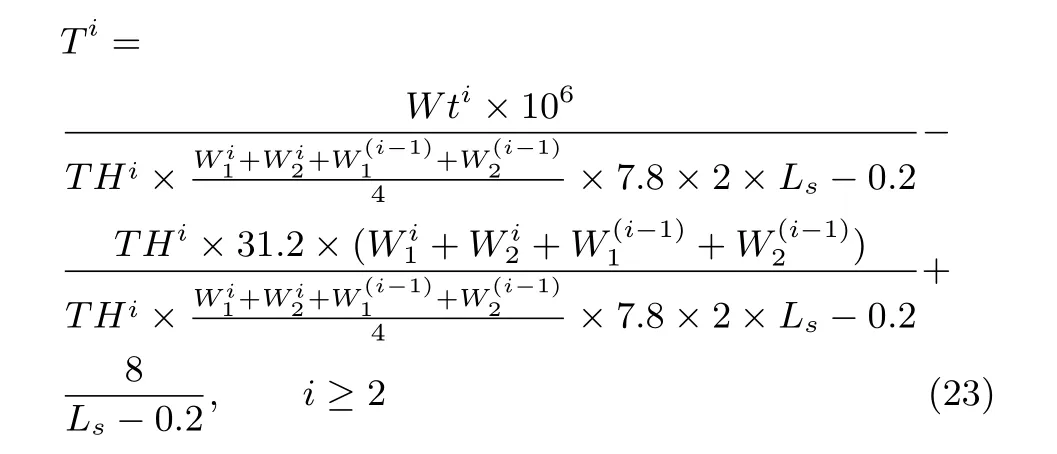
式中,Wti为第i炉钢水的总重量(吨);THi为浇铸第i炉钢水输出板坯的平均厚度(毫米);为浇铸第i炉钢水输出板坯的平均左、右宽度(毫米);为浇铸第(i−1)炉钢水输出板坯的平均左、右宽度(毫米);Ls为连铸机的标准拉速(米/分钟).

2)按照动态规划模型为每个炉次指派加工的设备:

a)计算每个炉次在连铸上的开浇时间xij(k6);

b)利用基本方程即式(9)递推每个炉次在每个阶段的开始作业时间xij(kg(θ));

c)利用最优指标函数即式(10)求出炉次Lij的最优指标函数值Fij(k1,k2,···,ϑij);

e)对每个炉次重复步骤c)～e),直到所有的炉次全部安排完为止.

3.2 第二阶段求解冲突解消模型

1)利用已开发的求解线性规划软件包(称为LP)对冲突解消模型进行求解,但在使用前需要做一个程序转换接口,即将设备指派模型的结果转化成第二个阶段用LP程序求解的输入条件,然后调用LP即可.也可以用Lingo等软件进行求解.

2)将求出的解(x1,x2,···,xn)转化成对应设备的作业开始时间,在利用设备处理时间,就可以得到在该设备上的结束时间,从而形成调度时刻表.

4 工业实验

4.1 实验数据

表1是3个浇次10个炉次计划的现场实际数据.其中开浇时间分别为:第一个浇次7:17;第二浇次7:10;第三个浇次7:25,其他信息见表1.

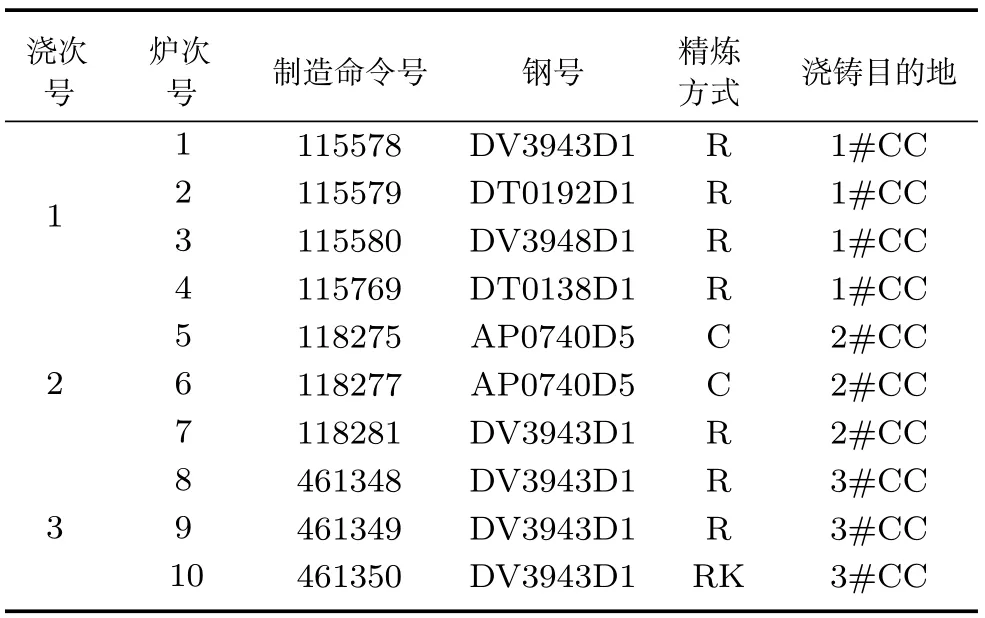
表1 三个浇次10个炉次计划的初始数据Table 1 Initial data of three cast including ten charges

4.2 实验结果

表2是采用本文所建立的动态规划模型为表1中的10个炉次确定出的具体加工设备,对应的处理时间和运输时间由现场给出,见表2.

表2 基于动态规划的设备指派结果Table 2 Equipment assignment base on dynamic programming

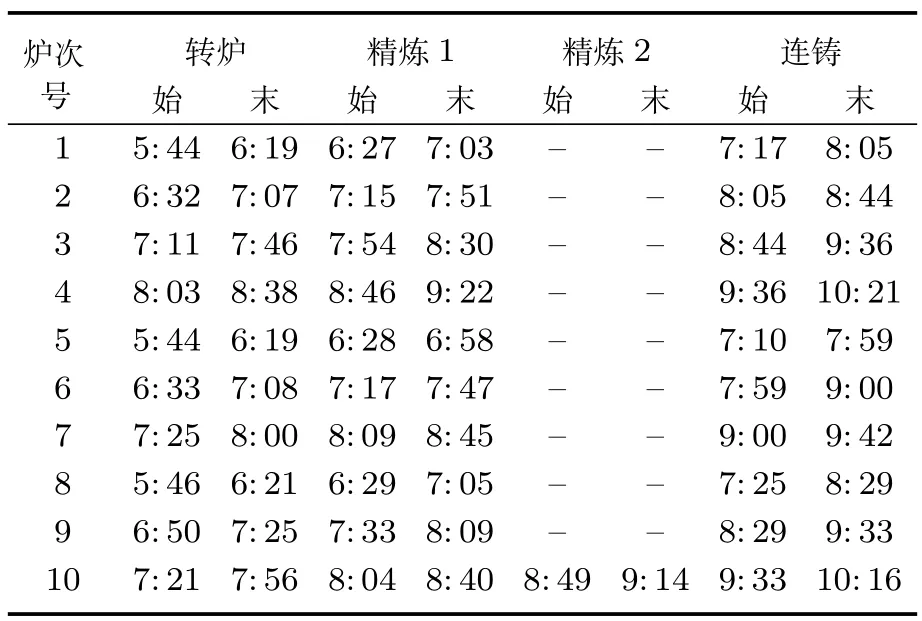
表3 基于动态规划的10个炉次粗调度时刻表Table 3 Ten charges rough schedule base on dynamic programming

由动态规划模型计算出10个炉次在各设备上的作业时间见表3.由于表3不易看出哪个炉次在那个设备上与哪个炉次有冲突,所以将表3用甘特图表示,见图2.从图2可以清楚地看出,第三个浇次中的炉次9与炉次10在1#LD设备上存在设备冲突,在3#RH也存在冲突.利用第二阶段建立的冲突解消模型求解后,得到无冲突的作业时间表和对应的甘特图分别见表4和图3.其中冲突解消模型中的惩罚系数由文献[19]的方法确定,惩罚系数分别为:C1=20,C2=10,C3=30,C4=15.

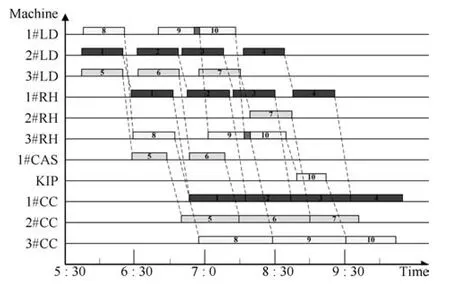
图2 基于动态规划10个炉次的粗调度甘特图Fig.2 Gantt chart of ten charges rough scheduling based on dynamic programming

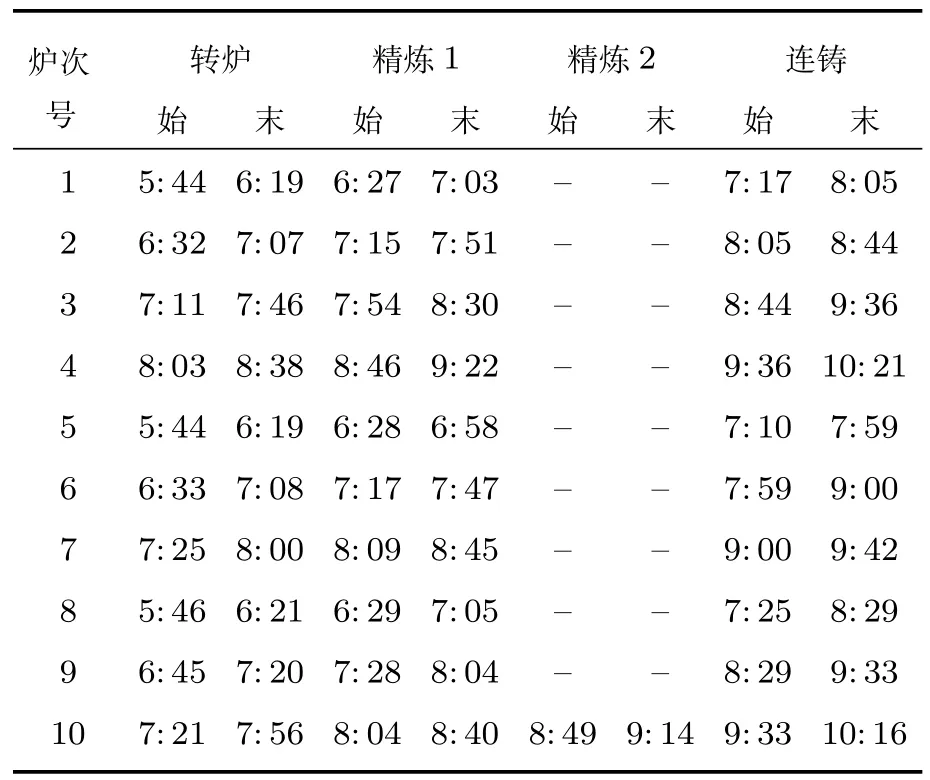
表4 10个炉次机器冲突解消后的调度表Table 4 Ten charges schedule table after conflicts eliminated

5 结论

本文研究了面向国内某大型钢厂炼钢–连铸生产调度过程的两阶段优化建模及求解策略.首先,根据该厂的设备条件和调度需求定义了符合调度过程的符号、调度目标和工艺约束条件,并给出了建模及求解的详细过程.解决了对于具有并行机的多设备、工艺复杂,采用常规建模及求解方法难以满足现场对调度快速响应及求解精度的问题.本文提出的两阶段优化建模方法不仅在解的精度及速度能满足现场的需要,而且当用户想采用一种新的算法求设备指派模型时,无需对整个调度算法的程序进行修改,只需用新的设备指派程序替换旧的设备指派程序即可.从而减少程序开发人员的重复劳动,易于增加调度问题求解算法的多样性和灵活性.

图3 10个炉次冲突解消后的调度甘特图Fig.3 Scheduling Gantt chart after ten charges machine conflicts eliminated

1 Wu Qi-Di,Qiao Fei,Li Li,Wu Ying.Data-based scheduling for complex manufacturing processes.Acta Automatica Sinica,2009,35(6):807−813 (吴启迪,乔非,李莉,吴莹.基于数据的复杂制造过程调度.自动化学报,2009,35(6):807−813)

2 Wang Xiu-Ying,Chai Tian-You,Zheng Bing-Lin.Intelligent scheduling software&its application in steelmaking and continuous casting.Computer Integrated Manufacturing Systems,2006,12(8):1220−1226 (王秀英,柴天佑,郑秉霖.炼钢–连铸智能调度软件的开发及应用.计算机集成制造系统,2006,12(8):1220−1226)

3 Missbauer H,Hauber W,Stadler W.A scheduling system for the steelmaking-continuous casting process.A case study from the steel-making industry.International Journal of Production Research,2009,47(15):4147−4172

4 PacciarelliD,PranzoM.Production schedulingin a steelmaking-continuouscasting plant.Computersand Chemical Engineering,2004,28(12):2823−2835

5 Huang Min,Fu Ya-Ping,Wang Hong-Feng,Zhu Bing-Hu, Wang Xing-Wei.Job-shop scheduling model and algorithm with machine deterioration.Acta Automatica Sinica,2015, 41(3):551−558 (黄敏,付亚平,王洪峰,朱兵虎,王兴伟.设备带有恶化特性的作业车间调度模型与算法.自动化学报,2015,41(3):551−558)

6 Bellabdaoui A,Teghem J.A mixed-integer linear programming model for the continuous casting planning.International Journal of Production Economics,2006,104(2): 260−270

7 Mao K,Pan Q K,Pang X F,Chai T Y.A novel Lagrangian relaxation approach for a hybrid flowshop scheduling problem in the steelmaking-continuous casting process.European Journal of Operational Research,2014,236(1):51−60

8 Tang L X,Zhao Y,Liu J Y.An improved differential evolution algorithm for practical dynamic scheduling in steelmaking-continuous casting production.IEEE Transactions on Evolutionary Computation,2014,18(2):209−225

9 Sbihi A,Bellabdaoui A,Teghem J.Solving a mixed integer linear program with times setup for the steel-continuous casting planning and scheduling problem.International Journal of Production Research,2014,52(24):7276−7296

10 Yu Sheng-Ping,Chai Tian-You.Rescheduling method for starting time delay in steelmaking and continuous casting production processes.Acta Automatica Sinica,2016,42(3): 358−374 (俞胜平,柴天佑.开工时间延迟下的炼钢–连铸生产重调度方法.自动化学报,2016,42(3):358−374)

11 Tan Y Y,Liu S X.Models and optimisation approaches for scheduling steelmaking-refining-continuous casting production under variable electricity price.International Journal of Production Research,2014,52(4):1032−1049

12 Li Tie-Ke,Su Zhi-Xiong.Two-stage genetic algorithm for SM-CC production scheduling.Chinese Journal of Management Science,2009,17(5):68−74 (李铁克,苏志雄.炼钢连铸生产调度问题的两阶段遗传算法.中国管理科学,2009,17(5):68−74)

13 Atighehchian A,Bijari M,Tarkesh H.A novel hybrid algorithm for scheduling steel-making continuous casting production.Computers&Operations Research,2009,36(8): 2450−2461

14 Pan L,Yu S P,Zheng B L,Chai T Y.Cast batch planning for steelmaking and continuous casting based on ant colony algorithm.In:Proceedings of the 2010 International Symposium on Computational Intelligence and Design.Hangzhou, China:IEEE,2010.244−247

15 Li J Q,Pan Q K,Mao K,Suganthan P N.Solving the steelmaking casting problem using an effective fruit fly optimisation algorithm.Knowledge-Based Systems,2014,72: 28−36

16 Pan Q K.An effective co-evolutionary artificial bee colony algorithm for steelmaking-continuous casting scheduling. European Journal of Operational Research,2016,250(3): 702−714

17 Wang X Y,Jiang X J,Wang H H.Optimal modeling and analysis of steelmaking and continuous casting production scheduling.In:Proceedings of the 11th World Congress on Intelligent Control and Automation.Shenyang,China: IEEE,2014.5057−5062

18 Wang Xiu-Ying.Hybrid Optimization Scheduling Method of Steelmaking and Continuous Casting and its Application [Ph.D.dissertation],Northeastern University,China,2012 (王秀英.炼钢–连铸混合优化调度方法及应用[博士学位论文],东北大学,中国,2012)

19 Wang Xiu-Ying,Chai Tian-You,Zheng Bing-Lin.Parameter optimization setting of steel making and continuous casting scheduling model.Journal of Systems Science and Systems Engineering,2011,26(4):531−537 (王秀英,柴天佑,郑秉霖.炼钢–连铸调度模型参数优化设定方法.系统工程学报,2011,26(4):531−537

王秀英 青岛科技大学信息科学技术学院教授.2012年获得东北大学博士学位.主要研究方向为生产计划与调度理论和方法,智能优化算法.本文通信作者.

E-mail:bywxy@126.com

(WANGXiu-Ying Professor at the School of Information Science and Technology,Qingdao University of Science and Technology.She received her Ph.D.degree from Northeastern University in 2012.Her research interest covers theory and method of production planning and scheduling,and intelligent optimization algorithms.Corresponding author of this paper.)

冯 惠 青岛科技大学信息科学技术学院硕士研究生.主要研究方向为智能优化算法,生产计划与生产调度.

E-mail:huifeng0411@163.com

(FENG HuiMaster student at the School of Information Science and Engineering,Qingdao University of Science and Technology.Her research interest covers intelligent optimization algorithm,production planning and scheduling.)

任志考 青岛科技大学信息科学技术学院副教授.主要研究方向为智能优化算法,无线网络技术,机器人通信,云服务技术.E-mail:rzk_888@163.com

(REN Zhi-Kao Associated professor at the School of Information Science and Technology,Qingdao University of Science and Technology.His research interest covers intelligent optimization algorithms,wireless network technology, robot communication and cloud-service technology.)

周艳平 青岛科技大学信息科学技术学院副教授.分别于2003年和2013年在青岛科技大学和华东理工大学获得硕士和博士学位.主要研究方向为智能优化算法,生产计划与生产调度.

E-mail:zypweb@163.com

(ZHOU Yan-Ping Associated professor at the School of Information Science and Technology,Qingdao University of Science and Technology.He received his master degree from Qingdao University of Science and Technology in 2003,and Ph.D.degree from East China University of Science and Technology in 2013.His research interest covers intelligent optimization algorithm, production planning and scheduling.)

Two-stage Optimal Modeling and Algorithm of Production Scheduling for Steelmaking and Continuous Casting

WANG Xiu-Ying1FENG Hui1REN Zhi-Kao1ZHOU Yan-Ping1

Steelmaking and continuous casting production scheduling is a multi-equipment assignment,multi-objective, multi-constraint,discrete and continuous variables hybrid optimization problem.Traditional modeling and solving methods are usually adopted to solve it,but they cannot meet the requirement in terms of high scheduling accuracy and fast problem solving speed.A new two-stage optimal modeling algorithm is proposed in this paper.In stage one,we show that minimizing the waiting time from steelmaking to continuous casting is equivalent to maximizing the converter operating time at first.Then we built a multiple-stage dynamic programming equation and optimization model using discrete variables,with the goal of maximizing the converter operating time.In stage two,we establish a linear programming conflict elimination model using continuous variables by converting a non-linear performance index into two equavalent linear optimization indexes including lead time,lag time between pratical casting and planned casting,and combining the other two indexes including time gap between furnaces on same caster and waiting duration for steel ladle among converters,refining furnaces and casters.On-site industry application validates that the proposed method can solve the scheduling problem with high speed and accuracy.

Steelmaking and continuous casting,production scheduling,optimal modeling strategy,equipment assignment model,conflict solving model

王秀英,冯惠,任志考,周艳平.面向炼钢–连铸调度过程的两阶段优化模型与算法.自动化学报,2016,42(11): 1702−1710

Wang Xiu-Ying,Feng Hui,Ren Zhi-Kao,Zhou Yan-Ping.Two-stage optimal modeling and algorithm of production scheduling for steelmaking and continuous casting.Acta Automatica Sinica,2016,42(11):1702−1710

2016-01-06 录用日期2016-06-22

Manuscript received January 6,2016;accepted June 22,2016

国家自然科学基金 (61104004), 山东省自然科学基金(ZR2014FL019),山东省高等学校科技计划项目(J14LN31)资助

Supported by National Natural Science Foundation of China (61104004),Natural Science Foundation of Shandong Province (ZR2014FL019),Higher Educational Science and Technology Program of Shandong Province(J14LN31)

本文责任编委赵千川

Recommended by Associate Editor ZHAO Qian-Chuan

1.青岛科技大学信息科学技术学院青岛266000

1.College of Information Science and Technology,Qingdao University of Science and Technology,Qingdao 266000

DOI 10.16383/j.aas.2016.c160005