基于混合特征的非刚性点阵配准算法

汤昊林 杨扬,2 杨昆,2 罗毅,2 张雅莹 张芳瑜

基于混合特征的非刚性点阵配准算法

汤昊林1杨扬1,2杨昆1,2罗毅1,2张雅莹1张芳瑜1

提出一种基于混合特征的非刚性点阵配准算法.该算法包含了对应关系评估与空间变换更新两个相互交替的步骤.首先定义了两个特征描述法用于描述两个点阵之间的全局和局部几何结构特征差异,随后合并这两个特征描述法建立一个基于混合特征的能量优化方程.该能量优化方程可以利用线性分配技术进行求解,同时可以灵活地选择使用最小化全局结构特征差异或最小化局部结构特征差异来评估两个点阵之间的对应关系.为了增强前述两个步骤之间的协调性,我们利用能量权重调节在整个配准过程中控制能量优化从最小化局部结构特征差异逐步转变为最小化全局结构特征差异,同时控制用于空间变换的薄板样条函数(Thin plate spline)的更新从刚性变换逐步转变为非刚性变换.我们在二维轮廓配准、三维轮廓配准、序列图像配准和图像特征点配准下对本文算法进行了各项性能测试,同时也与当前8种流行算法进行了性能比较.本文算法展现了卓越的非刚性配准性能,并在大部分实验中超越了当前的相关算法.

非刚性,点阵配准,混合特征,对应关系评估,空间变换更新

非刚性点阵配准(Non-rigid point set registration)是将某一点阵(称为源点阵)与其发生形变后的点阵(称为目标点阵)进行匹配的过程.该技术在计算机视觉、机器学习、医学图像处理、模式识别以及地理信息系统中扮演着极其重要的角色.基于当前算法的特点,非刚性点阵配准算法大体可以分为两大类:基于迭代或非迭代的算法和基于学习或非学习的算法.由于本文算法主要涉及基于迭代的问题,所以我们主要从基于迭代或非迭代的角度来介绍当前的非刚性点阵配准算法.

在基于非迭代的非刚性点阵配准算法中,两组点阵之间的对应关系是通过使用某种高级结构特征(High level structural features)仅进行一次相似性评估后直接找回两组点阵之间的对应关系.在基于非迭代的配准模型中,直线[1]、曲线[2]、表面结构[3]、Shape context[4−5]和图论(Graphs)[6−7]等特征被用于两个点阵之间相似度的评估.在非迭代算法中,Shape context和Graphs是最受欢迎的两种特征描述法,其核心是通过最小化两个点阵之间的分布差异(使用Shape context时)或者拓扑结构差异(使用Graphs时)来找回点阵之间的对应关系[4−9].最近,一部分研究人员[10−14]在传统的基于Graphs特征算法的基础上加入了学习要素,通过在配准前使用适当的学习样本进行学习来优化算法中的参数设置,从而提高了算法的配准精度.但是这类算法由于使用了Shape context或Graphs特征,当相邻点较为接近时该类特征则变得非常相似以至于这类算法并不能达到较好的配准效果[8,15−16].

基于迭代的算法通常包括两个相互交替的过程:对应关系评估(Correspondence estimation)和空间变换更新(Transformation updating).相对于基于非迭代的算法,基于迭代的算法的优势在于它们在迭代过程中逐步地调整源点阵的初始几何形状和空间位置使得源点阵在几何形状和空间位置上变得越来越接近目标点阵,从而使得通过几何结构特征寻找它们之间的对应关系变得更加容易. TPS-RPM[17]是第一个利用迭代技术来进行非刚性点阵配准的算法.它通过使用点阵到点阵的距离、Softassign[18−19]和退火算法[20−21]来评估点阵之间的对应概率和控制薄板样条函数(Thin plate spline,TPS)[22]的更新.Myronenko等[23]在TPSRPM 算法框架基础上提出了在空间变换更新中增加运动一致性约束条件(Motion coherence constraint)[24]来提高配准过程中空间变换的稳定性,并利用最大似然法(Maximum likelihood)来评估点阵之间的对应关系.之后,Myronenko等[25]在文献[23]的基础上发表了著名的CPD算法(Coherent points drift algorithm),他们改良了空间变换模型使之既可以适用于刚性和非刚性的点阵配准问题,并可以在配准精度要求相对不高的情况下通过使用快速高斯变换(Fast Gauss transform)[26]和矩阵低秩逼近(Low-rank matrix approximation)[27]技术减少计算量来提升算法的配准速度.近期, Jian等[16]提出了一种基于高斯混合模型(Gaussian mixture model)的非刚性点阵配准算法(称为GMMREG).该算法不直接在几何空间中配准两个点阵,而是把两个点阵先转变成为两个高斯混合模型,然后在这基础上进行对应关系评估,空间变换更新基于最小化两个高斯混合模型的L2距离[28].最近,国内的Ma等[29]提出了一种基于Shape context特征和L2E评估[30]的算法,Wang等[31]通过使用不对称的高斯模型捕捉空间点阵的不对称分布,并用其作为特征描述进行点阵的非刚性配准.

本文中,我们提出了一种基于混合特征的非刚性点阵配准算法.本算法的主要贡献体现在以下3个方面:

1)全局结构特征描述算法:我们提出了一种利用和向量来描述点阵中各点的全局结构特征的描述算法.

2)局部结构特征描述算法:我们提出了一种利用点阵之间的局部区域相邻点的距离和描述点阵中各点的局部结构特征的描述算法.

3)基于混合特征的点阵对应评估算法:我们通过混合全局和局部结构特征描述算法提出了一种基于混合特征的能量方程,该方程允许使用混合特征进行点阵对应评估,使得在配准过程中所使用的特征不再单一化,使配准精度得到了提高并在大部分实验中超越了当前相关算法.

1 方法

我们首先定义了全局和局部特征描述法以及混合特征能量优化方程,然后对本文算法的两个核心步骤进行介绍.在本章的后面部分,我们将对本文算法的参数设定以及本文算法与当前相关方法的差异进行说明.假设和是两组需要进行配准的点阵,分别为源点阵和目标点阵.

1.1 全局和局部结构特征差异

1.1.1 全局结构特征差异

全局几何结构特征差异被定义为

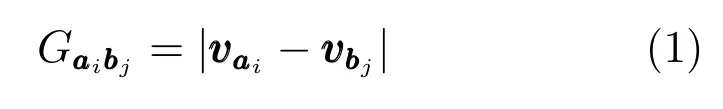
1.1.2 局部结构特征差异

局部结构特征差异被定义为

在这里,我们使用Linear assignment技术来最小化全局结构特征差异矩阵与局部结构特征差异矩阵我们将会获得两种对应关系,它们分别是基于最小化的全局结构特征差异和局部结构特征差异计算而来的.

1.2 基于混合特征的能量优化方程

本文中提出的基于混合特征的能量优化方程被定义为

1.3 配准过程

1.3.1 步骤1:对应关系评估

对于线性分配中的Integer cost问题,在配准前我们首先将需要配准的点阵坐标缩放至[0,1]之间,然后在每一次迭代中把计算出的全局与局部结构特征差异矩阵通过使用和⌉进行数值处理,其中R被设为106.对于非方形矩阵问题(点阵b bb包含冗余点),非方形矩阵和可以通过分配虚拟项(Dummy entries)[33]来转换为方形矩阵,而且不会影响整体能量优化.转换后E(M)则可以使用通常手段求解,并且仍然给出最优解.虽然我们提供了一种针对目标点阵包含冗余点的配准解决方案,但是本文算法并不能很好地处理包含冗余点的配准问题.原因是用于描述各点全局结构特征的和向量容易受冗余点的影响.

通过使用Jonker-Volgenant算法求解的对应关系矩阵M确保了从点阵到点阵的一一对应关系.当前迭代的对应点集由式(7)进行更新

本文提出的基于混合特征的能量优化方程为使用混合特征来评估对应关系提供了一个灵活方法.例如,当α非常大时,最小化E等于最小化局部结构特征差异求出的点对点的对应关系是基于最小化两个点阵之间的局部结构特征差异.当α逐渐变小时,对应关系评估开始转向使用最小化全局结构特征差异,求出的点对点的对应关系是基于最小化两个点阵之间的全局结构特征差异.

1.3.2 步骤2:空间变换更新

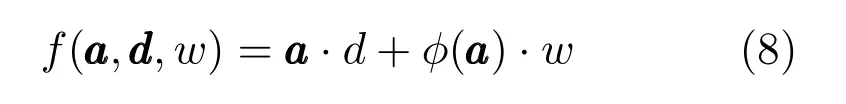
其中正规化参数λ用于调节非刚性形变系数w,同时它也被前述使用在式(6)中用来控制权重参数α的能量权重调节所控制.Φ是TPS内核矩阵,由前述TPS内核方程φ(a aa)计算而来.

为了计算d和w的最小二乘解,矩阵的QR分解技术[34]被用于分离点阵的仿射和非刚性形变空间

其中,Q1∈RN×D,Q2∈RN×(N−D),R1∈RD×D.此外,Q1与Q2拥有相同的正交列.所以式(9)可以转换为

其中w=Q2γ,γ∈R(N−D−1)×(D+1).式(11)的最小二乘解可以通过先最小化γ,然后最小化d来求解.w和d的解为

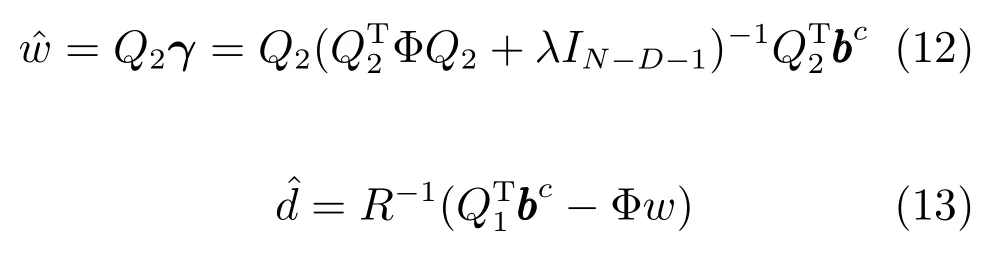
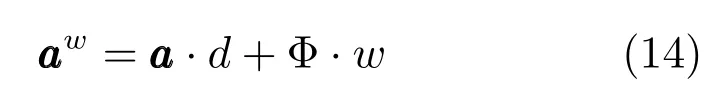
1.4 算法伪代码及参数设置

算法1给出了本文算法的伪代码.

算法1.基于混合特征的非刚性配准算法

预处理.初始化参数Tinit,Tfinal,r,λinit和αinit.设定K并且确定点阵的相邻点集

开始.能量权重调节计划.

步骤2.使用式(12)和(13)更新TPS空间变换.

通过调节减小T,然后更新参数α和λ.

结束.直至满足T≤Tfinal.

本文提出的基于混合特征的非刚性点阵配准算法包含四组重要参数:调节参数Tinit,Tfinal和r,权重参数α,正规化参数λ以及相邻点个数参数K.每组参数的详细设定如下

1)调节参数:能量权重调节中所使用的T[20−21]在配准开始前被设定为一个较高的值Tinit,随后在每次迭代中利用一个线性调节计划T=T×r使得T值在配准过程中被逐步降低,其中r为调节率.当到达一个较低的设定值Tinit时,调节计划停止.本文中设计该线性调节计划的目的主要有2方面:首先利用T来逐步减小式(6)中的权重参数α,使得式(6)的能量优化问题可以从首先最小化局部结构特征差异逐步过度到最小化全局结构特征差异;其次利用T来逐步减小式(9)和(12)中的正规化参数λ,使得TPS空间变换可以从更加刚性的形变更新逐渐转化为更加非刚性的形变更新.由于调节参数从根本上决定了算法迭代的次数,所以Tinit,Tfinal和r的参数设定原则为满足配准所需的足够迭代次数.基于前期使用Fish 1点阵[17]进行的试错实验(Trial-and-error experiment),起始Tinit值被设为点阵到最大距离平方的1/10,终止Tfinal值被设为点阵中各点到其最近点平均距离平方的1/8,调节率r通常被设为0.7.

2)权重参数:权重参数α在每次迭代中,通过使用α=αinit×T被逐渐减小,α的初始值设定原则为能够保证在配准前期整个算法可以集中在利用最小化局部结构特征差异来评估点阵的对应关系.初始值αinit被设为相邻点个数的平方K2.

3)正规化参数:正规化参数λ在每次迭代中,通过使用λ=λinit×T被逐渐减小,由于λ主要用来控制TPS变换中的刚性和非刚性形变(λ较大时, TPS呈现出刚性变换;λ较小时,TPS转为呈现非刚性形变),所以λ的初始值设定原则为能够确保在配准前期TPS处于刚性变换.初始值λinit被设为点阵a a

a中点的数量.

4)相邻点数量参数:参数K的默认值设定是基于用于区别局部结构差异所需的最少相邻点数.例如,当我们需要区别角(Corner,其中包含2个相邻点)和十字(Cross,其中包含4个相邻点)时,我们至少需要借助4个相邻点来判断.基于上述考虑,我们将参数K在二维和三维配准情况下的默认值设为5.

2 相关研究

当前主要有TPS-RPM[17],CPD[25],GMMREG(L2+TPS)[16],Ma等[29]和Wang等[31]5种算法与本文算法相似,表1详细列举了本文算法与上述5种算法之间存在的差异.

表1 本文算法与相关算法的不同Table 1 Methodological differences between our method and the current methods

1)对应关系评估:与上述基于单一特征配准的5种算法不同,本文算法是一种基于混合特征的能量优化问题,且允许使用混合特征进行点阵之间的对应关系评估.因为本文算法与Ma等使用了线性分配技术求解对应关系,所以我们都提供了一个二值对应关系,即在对应关系矩阵Mij中仅使用0和1来描述对应关系.在TPS-RPM,CPD,GMMREG和Wang等[31]算法中,空间变换方程是建立在模糊对应(Fuzzy correspondences,即对应概率)关系基础上的,所以在指导代理点阵改变其空间位置和几何形状时会发生模糊更新,同时也会需要更多的迭代次数才能完成配准.在本文算法中,建立在最小化全局或局部结构特征差异的二值对应关系可以为代理点阵提供一个正确且清晰的空间位置与几何形状的更新指导.

2)空间变换更新:本文算法使用的是标准TPS能量方程.TPS-RPM 在式(6)中增加了λ2tr[d−I]T[d−I]项用于控制仿射参数.由于本文算法在每次迭代中提供了一个较为精确的二值对应关系给TPS空间变换,所以我们仅需要使用λ来控制w系数在刚性和非刚性变换上的作用.同时一个自由的仿射变换(也就是不受控制的仿射系数d)可以帮助代理点阵快速(使用更少的迭代次数)地找到更加接近目标点阵的空间位置和几何形状来完成接下来的非刚性配准.此外,与CPD中强制相邻点集保持运动一致性不同,本文算法通过在整个配准过程中固定相邻点集和来保护代理点阵的拓扑结构特征.

3 实验

我们使用Matlab实现了本文算法的主要过程,其中Jonker-Volgenant算法使用C++编写并利用Matlab mex function调用Jonker-Volgenant算法的C++函数.我们首先基于以下四种配准模式测试了本文算法的各项性能,

1)轮廓配准(2D synthetic point set);

2)3D轮廓配准(3D face point set);

3)序列图像(CMU house and CMU hotel sequence);

4)真实图像特征点配准(Pascal 2007 challenge datasets).

而且,本文算法还与下列当前典型的8种算法进行了性能比较实验,

1)基于迭代的算法:TPS-RPM[17],CPD[25], GMMREG(L2+TPS)[16],Wang等[31];

2)基于Graph的学习算法:Caetano等[10], Leordeanu等[13],Torresani等[14];

3)基于Graph的非学习算法:Zhou等[9].

最后,我们评估了本文算法的计算复杂度并且讨论了如何降低本文算法的计算复杂度.

3.1 实验设计

Line[17]、Fish 1[17]、Fish 2[25]、Chinese character[17]和3D face[25]是非刚性点阵算法在轮廓点阵配准测试中普遍使用的几个流行点阵,它们分别来自TPS-RPM[17]和CPD[25].本文首先使用这5个点阵作为源点阵,并使用下面人工合成的方法创建了一系列丰富的目标点阵与TPS-RPM,CPD和GMMREG进行了性能对比实验.为了达到公平的实验对比,在目标点阵的生成、误差测量和性能评估上我们遵循了TPS-RPM[17]和CPD[25]中所用的方法.由于本文中提出的全局特征描述法(见第1.1.1节)是由和向量设计而来,当配准目标点阵中包含冗余点时,本文算法并不能很好地处理包含冗余点的配准问题,所以在本实验中我们不进行包含冗余点的配准模式性能测试.

目标点阵:

1)形变级别:我们设置8个控制点(三维配准情况是为6个控制点)在每组轮廓点阵边缘.为了创建一系列不同形变级别且适合的目标点阵,每个控制点拥有上、下、左、右4个方向的自由移动以及0.2的移动步长.8个(或6个)控制点的移动循序以及方向被随机设定.在本实验中,TPS空间变换被用于使用这8个(或6个)控制点使前述源点阵发生形变创建新目标点阵.因为被移动的控制点数量反映了点阵的形变大小,所以本实验中形变级别被定义为移动控制点的数量(二维和三维情况下的最大形变级别分别为8和6).

2)噪音比:我们通过利用均值为0且标准偏差从0.01至0.05的高斯白噪声(Gaussian white noise)创建了5个噪音级别的目标点阵.

3)旋转角度:我们认为在适当旋转下的配准性能测试是必要的,因为通常形变发生时都会伴随着旋转.但是过大旋转会导致相关算法产生不稳定或无价值的配准结果,所以我们主要专注于在以15°为间隔,旋转−30°到30°的情况下的配准性能测试.在三维配准实验中,源点阵被沿Z轴旋转来创建新目标点阵.

误差测量:在误差测量中,通常可以选择的测量方法很多.例如,正确匹配百分比、配准后点阵之间的平均距离等.为了保证直接和公平的比较,我们遵循了TPS-RPM与CPD中的误差测量法,即代理点阵与目标点阵之间平均距离的平方.

性能评估:平均误差(即100次测试中的平均距离平方与标准偏差)在本实验中被用来比较不同算法之间的配准性能.对于每组点阵,在每种形变级别、噪音比、旋转角度下执行了100次的随机实验.

3.2 二维轮廓点阵的配准结果

在第一系列的实验中,我们在不同的二维人造轮廓点阵上评估了本文算法的性能.与后面的序列图像(CMU sequences and Pascal 2007 challenge)以及真实图像特征点(Pascal 2007 challenge)配准相比,这些二维轮廓点阵拥有更多的点数以及较密的点阵分布.在这类点阵配准中,由于相邻点彼此靠近且拥有相似的局部结构特征,所以在评价各点的局部特征结构相似度时变得更加困难.本文算法与相关算法的比较结果如下.

3.2.1 Line

在点阵Line的配准测试中,本文算法仅与TPS-RPM 进行对比测试.因为其他算法并没有在该点阵上进行测试并公布相关的参数设定.性能测试统计数据(平均误差与标准偏差)展示在图1的第1行.本文算法在所有的实验中展现了准确的配准结果,并且在所有形变级别、噪音比、旋转角度的测试中,给出了最优的配准结果.图2给出了本文算法的一个配准实例.

3.2.2 Fish 1

在点阵Fish 1的配准测试中,我们测试了本文算法与CPD,TPS-RPM和GMMREG的性能,图1的第2行展示了测试结果.这4种算法均给出了准确的配准结果,本文算法在所有的形变级别和所有旋转角度的测试中展现了最优的性能结果.在目标点阵含有噪音的配准测试中,这四种算法均展现了准确的配准结果,GMMREG表现得更好.图3给出了本文算法的一个配准实例.

3.2.3 Chinese character

在点阵Chinese character的配准测试中,本文算法仅与TPS-RPM进行对比实验.因为CPD与GMMREG并未在非刚性配准中测试过该点阵(GMMREG仅在刚性配准中测试过该点阵).本文算法在所有形变级别、噪音比从0.01至0.03、所有旋转角度的测试中给出了最优的配准结果.图4给出了一个本文算法的配准实例.

3.2.4 Fish 2

本文算法与CPD的性能测试结果展示在图1的第4行.本文算法在所有的实验中展现了准确的配准结果,并且在所有形变级别、噪音比以及旋转角度的测试中给出了最优的配准性能.图5给出了本文算法的一个配准实例.

图1 二维轮廓点阵配准下的性能对比(误差线表示了100次随机测试中平均误差的标准偏差值.从第1行至第4行分别为点阵Line,Fish 1,Chinese character以及Fish 2的实验结果.)Fig.1 Comparison of our results against CPD,TPS-RPM and GMMREG on 2D contour point set registration(The error bars indicate the standard deviations of the mean errors in 100 random experiments.From the top row to bottom row are:Line,Fish 1,Chinese character and Fish 2,respectively.)

在二维轮廓点阵配准测试中,所有的算法均给出了准确的配准结果,但是本文算法在形变与旋转测试中明显地超越了相关算法.

3.3 三维人脸点阵的配准结果

在第二系列的实验中,我们评估了本文算法在三维配准中的性能.本实验中使用的3D face点阵已被CPD和GMMREG等算法用于测试其在三维配准中的性能.图6给出了本文算法与CPD、GMMREG算法的性能测试结果.本文算法在所有实验中给出了准确的配准结果,同时在所有形变级别、噪音比从0.01至0.04以及所有旋转角度的实验中给出了最优的性能结果.图7给出了一个本文算法的配准实例.

3.4 序列图像的配准结果

在第三系列的实验中,我们测试了本文算法在序列图像特征点配准问题上的性能.与二维和三维人造点阵相比,序列图像拥有更少的特征点,这些点稀疏地分布在图像中.CMU house和CMU hotel序列图像是目前用于测试基于Graph的学习算法最流行的实验数据.两个序列图像分别由111和101幅图组成,每幅图拥有30个标记的特征点.在本实验中,我们使用正确配准点数的百分比(称为配准率)为误差测量法.

图2 本文算法的配准实例:LineFig.2 Registration examples on Line point set

图3 本文算法的配准实例:Fish 1Fig.3 Registration examples on Fish 1 point set

图4 本文算法的配准实例:Chinese characterFig.4 Registration examples on Chinese character point set

图5 本文算法的配准实例:Fish 2Fig.5 Registration examples on Fish 2 point set

图6 三维Face轮廓点阵配准下的性能对比(误差线表示了100次随机测试中平均误差的标准偏差值.)Fig.6 Comparison of our results against CPD and GMMREG on 3D face contour point set registration (The error bars indicate the standard deviations of the mean errors in 100 random experiments.)

图7 3D face点阵配准实例Fig.7 Registration examples on 3D face point set

本文算法与三种基于 Graph的学习算法[10,13−14],一种基于Graph的非学习算法[9],和三种基于迭代的算法[16,25,31]分别在这两组序列图像的所有配准可能中进行了性能对比实验.

表2展示了实验结果.在House序列图像的配准中,对于Caetano等[10]与Zhou等[9],我们报告了他们公布的配准率的上限值,对于Leordeanu等[13]、Torresani等[14]和Wang等[31],我们给出了他们公布的配准率.本文算法,Wang等[31]和Torresani等[14]给出了完美的配准结果,也超越了其他算法.但是从算法运行时间角度来看,本文算法的运行时间(平均0.049秒)比Torresani等公布的平均运行时间4.8秒[14]快了很多(该对比也考虑了使用电脑的性能问题).在CMU hotel序列图像的配准中,Wang等[14,31]与Zhou等[9]没有提供他们的实验结果.与CPD,GMMREG,Leordeanu等[13]和Caetano等[10]相比较,本文算法展现了更好的配准精度.图8给出了本文算法的两个配准实例.

表2 CMU house和CMU hotel序列图像中所有可能的图像配准结果(%)Table 2 Matching rates on the CMU house and CMU hotel for all possible image pairs(%)

图8 CMU house与CMU hotel配准实例Fig.8 Registration examples on CMU house and CMU hotel

3.5 图像特征点的配准结果

在第四系列的实验中,我们使用Leordeanu等[13]的测试数据测试了本文算法的性能.这套测试数据集从Pascal 2007 challenge数据库中挑选出来的,包含30对汽车图像与20对摩托车图像.每对图像中包含30～60个特征点.本文算法与CPD, GMMREG,Zhou等[9]和Leordeanu等[13]进行了性能对比,其结果在表3中列出,对于Zhou等[9](A)和Leordeanu等[13](B),我们报告了他们公布的实验结果.本文算法给出了最优的配准率.图9给出了本文算法的两个配准实例.

表3 汽车与摩托车图像库的配准结果(%)Table 3 Matching rates on cars and motorbikes(%)

3.6 计算复杂度

本文算法的计算复杂度主要与两个方面相关: 1)决定收敛性的能量权重调节参数Tinit,Tfinal与r;2)用于求解基于混合特征的能量优化方程的线性分配算法.

3.6.1 收敛范围

收敛范围主要与形变级别和能量权重调节参数设定相关.在其他相关算法中,TPS-RPM的收敛范围由退火算法决定,CPD和GMMREG则分别由容差停止准则(Tolerance stopping criterion)以及最大迭代次数所决定.我们调查了上述这四种算法在点阵Chinese character形变实验中的收敛范围.本文算法、TPS-RPM、CPD与GMMREG的参数设定值遵循前述Fish1实验中的设定值.CPD和TPS-RPM分别平均需要43次与85次迭代来完成整个配准过程,而GMMREG则需要最大迭代次数(100次)才能完成配准.原因是由于容差停止准则被设定为10−10,GMMREG在配准中最小化后的L2距离很难达到该标准.本文算法仅需要17次迭代就可以完成配准.

图9 Pascal 2007 challenge配准实例Fig.9 Registration examples on Pascal 2007 challenge

此外,我们也调查了本文算法在不同能量权重调节参数设定下的收敛范围.图10给出了在Chinese character点阵形变实验中的例子.对于每一个能量权重调节参数设定值,我们在每一个形变级别下运行了100次随机实验.基于图10展示的实验结果,随着调节初始值Tinit降低为默认值的1/10时,本文算法的性能发生了轻微的退化,配准所需迭代次数减少了41%(平均迭代次数从17次减少至10次);随着最终值Tfinal增加为默认值的10倍时,本文算法的性能发生了退化,配准所需迭代次数减少了41%(平均迭代次数从17次减少到10次);随着调节速率r减少为默认值的1/2,本文算法的性能轻微退化,配准所需迭代次数减少了65%(从17次减少至仅需6次).即便能量权重调节参数被显著地改变了,所有的实验依旧展现了非常高的配准精度(也就是误差低于0.0013且标准偏差在±0.0015之内).基于这些结果,本文算法的计算复杂度可以通过调整能量权重调节参数设定大幅降低,同时算法依旧维持了很高的配准精度.

图10 不同能量权重调节参数设定下的配准性能Fig.10 Relationships between performances and different energy tradeoff adjustment parameter settings

3.6.2 Jonker-Volgenant算法性能

为了使用线性分配技术求解二值对应矩阵M,本文算法使用了Jonker-Volgenant算法[32],该算法提供了O(N3)的计算复杂度.我们在一台4GB内存和2.67GHz Intel(R)Xeon(R)CPU的电脑上使用Matlab mex function功能测试了C++代码的Jonker-Volgenant算法性能.表4给出了使用Jonker-Volgenant算法求解不同大小的二值对应矩阵所需时间.Jonker-Volgenant算法展现了快速的求解能力,同时也为本文算法实现快速非刚性点阵配准提供了支撑.

表4 Jonker-Volgenant算法性能(测试矩阵由Matlab的rand函数自动生成.)Table 4 Performance of Jonker-Volgenant algorithm (The cost matrices were generated by Matlab rand function.)

4 结论

我们已经介绍了一种基于混合特征的非刚性点阵配准算法:1)设计出了一种基于和向量特征的全局结构特征描述算法;2)提出了一种利用点阵之间的局部区域相邻点的距离和描述点阵中各点的局部结构特征的描述算法;3)提出一种基于混合特征的能量方程并设计了该方程的能量权重调节,该方程允许使用混合特征进行点阵对应评估.最后将本文算法与8种当前典型算法进行了性能对比测试,本文算法在绝大多数的形变和旋转配准情况中展现了最好的配准结果.

致谢

感谢Chui Hai-Li,Rangarajan Anand,Myronenko Andriy,Song Xu-Bo,Jian Bing,Vemuri Baba,Zhou Feng,De la Torre Fernando, Leordeanu Marius,Torresani Lorenzo和Caetano Tiberio提供了他们的算法源代码和测试数据.这极大地促进了对比实验.我们无偿提供本文算法的Matlab源代码供学术研究.

1 Park S H,Lee K M,Lee S U.A line feature matching technique based on an eigenvector approach.Computer Vision and Image Understanding,2000,77(3):263−283

2 Kong W X,Kimia B B.On solving 2D and 3D puzzles using curve matching.In:Proceedings of the 2001 IEEE Conference on Computer Vision and Pattern Recognition.Kauai, HI,USA:IEEE,2001.II-583−II-590

3 Cochran S D,Medioni G.3-D surface description from binocular stereo.IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(10):981−994

4 Belongie S,Malik J,Puzicha J.Shape matching and object recognition using shape contexts.IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(4): 509−521

6 Balakrishnan V.Graph Theory(lst Edition).New York: McGraw-Hill,1997.

7 Sundar H,Silver D,Gagvani N,Dickinson S.Skeleton based shape matching and retrieval.In:Proceedings of the 2003 Shape Modeling International(SMI'03).Seoul,South Korea:IEEE,2003.130−139

8 Zheng Y F,Doermann D.Robust point matching for nonrigid shapes by preserving local neighborhood structures. IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(4):643−649

9 Zhou F,De la Torre F.Factorized graph matching.In:Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition.Providence,RI:IEEE,2012. 127−134

10 Caetano T S,Cheng L,Le Q V,Smola A J.Learning graph matching.In:Proceedings of the 11th IEEE International Conference on Computer Vision.Rio de Janeiro,Brazil: IEEE,2007.1−8

11 Leordeanu M,Hebert M.Smoothing-based optimization.In: Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition.Anchorage,AK:IEEE,2008. 1−8

12 Caetano T S,McAuley J J,Cheng L,Le Q V,Smola A J.Learning graph matching.IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(6):1048−1058

13 Leordeanu M,Sukthankar R,Hebert M.Unsupervised learning for graph matching.International Journal of Computer Vision,2012,96:28−45

14 Torresani L,Kolmogorov V,Rother C.A dual decomposition approach to feature correspondence.IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(2): 259−271

15 Xiao D,Zahra D,Bourgeat P,Berghofer P,Tamayo O A, Wimberley C,Gregoire M C,Salvado O.An improved 3D shape context based non-rigid registration method and its application to small animal skeletons registration.Computerized Medical Imaging and Graphics,2010,34(4):321−332

16 Jian B,Vemuri B C.Robust point set registration using Gaussian mixture models.IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(8):1633−1645

17 Chui H L,Rangarajan A.A new point matching algorithm for non-rigid registration.Computer Vision and Image Understanding,2003,89(2−3):114−141

18 Rangarajan A,Chui H,Bookstein F L.The softassign procrustes matching algorithm.In:Proceedings of the 15th International Conference on Information Processing in Medical Imaging.Poultney,Vermont,USA:Springer,1997. 29−42

19 Chui H L,Rambo J,Duncan J,Schultz R,Rangarajan A. Registration of cortical anatomical structures via robust 3D point matching.In:Proceedings of the 16th International Conference on Information Processing in Medical Imaging. Visegrd,Hungary:Springer,1999.168−181

20 Gold S,Rangarajan A,Lu C P,Pappu S,Mjolsness E.New algorithms for 2D and 3D point matching:pose estimation and correspondence.Pattern Recognition,1998,31(8): 1019−1031

21 Yuille A L.Generalized deformable models,statistical physics,and matching problems.Neural Computation,1990, 2(1):1−24

22 Bookstein F L.Principal warps:thin-plate splines and the decomposition of deformations.IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(6): 567−585

23 Myronenko A,Song X B,Carreira-Perpin M.Non-rigid point set registration:coherent point drift.In:Proceedings of the 2006 Advances in Neural Information Processing Systems 19.Cambridge,MA:MIT Press,2006.1009−1016

24 Yuille A L,Grzywacz N M.A mathematical analysis of the motion coherence theory.International Journal of Computer Vision,1989,3(2):155−175

25 Myronenko A,Song X B.Point set registration:coherent point drift.IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(12):2262−2275

26 Greengard L,Strain J.The fast Gauss transform.SIAM Journal of Scientific and Statistical Computing,1991,12(1): 79−94

27 Markovsky I.Structured low-rank approximation and its applications.Automatica,2008,44(4):891−909

29 Ma J Y,Zhao J,Tian J W,Tu Z W,Yuille A L.Robust estimation of nonrigid transformation for point set registration. In:Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition.Portland,OR:IEEE,2013. 2147−2154

30 Scott D W.Parametric statistical modeling by minimum integrated square error.Technometrics,2001,43(3):274−285

31 Wang G,Wang Z C,Chen Y F,Zhao W D.A robust nonrigid point set registration method based on asymmetric Gaussian representation.Computer Vision and Image Understanding,2015,141:67−80

32 Jonker R,Volgenant A.A shortest augmenting path algorithm for dense and sparse linear assignment problems. Computing,1987,38(4):325−340

33 Miller M L,Stone H S,Cox I J.Optimizing Murty's ranked assignment method.IEEE Transactions on Aerospace and Electronic Systems,1997,33(3):851−862

34 Wahba G.Spline Models for Observational Data.Philadelphia:SIAM,1990.

汤昊林 云南师范大学信息学院本科生.主要研究方向为图像配准以及医学图像处理.

E-mail:m18487107138@163.com

(TANGHao-Lin Undergraduate student at the School of Information Science and Technology,Yunnan Normal University. His research interest covers non-rigid point set registration and medical imaging.)

杨 扬 云南师范大学信息学院讲师. 2007年获得日本早稻田大学计算机硕士学位,2013年获得新加坡国立大学NGS博士学位.主要研究方向为医学图像处理,图像配准,地理空间信息技术,人体咀嚼系统.本文通信作者.

E-mail:yyang_ynu@163.com

(YANG Yang Lectureratthe School of Information Science and Technology,Yunnan Normal University.He received his master degree from Waseda University,Japan in 2007,and Ph.D.degree from National University of Singapore,Singapore in 2013.His research interest covers medical image processing,image registration,geography information system and human masticatory system.Corresponding author of this paper.)

杨 昆 云南师范大学信息学院教授, 1998年获得澳大利亚新南威尔士大学硕士学位.主要研究方向为地理信息系统,遥感图像处理.

E-mail:kmdcynu@163.com

(YANG Kun Professoratthe SchoolofInformation Science and Technology,Yunnan Normal University.He received his master degree from University of New South Wales,Australia in 1998.His research interest covers geographic information system(GIS)and remote sensing image processing.)

罗 毅 云南师范大学信息学院软件工程系讲师.2014年获得哈尔滨理工大学博士学位.主要研究方向为无线传感器网络,微弱信号拾取,视觉检测技术.

E-mail:luoyi861030@163.com

(LUO Yi Lecturer in the Department of Software Engineering,Yunnan Normal University. He received his Ph.D.degree from Harbin University of Science and Technology in 2014.His research interest covers wireless sensor networks,weak signal detection,and visual detection.)

张雅莹 云南师范大学信息学院本科生.主要研究方向为非刚性点阵配准和医学图像处理.

E-mail:nw_zhyaying@163.com

(ZHANG Ya-Ying Undergraduate student at the School of Information Science and Technology,Yunnan Normal University.Her research interest covers non-rigid point set registration and medical imaging.)

张芳瑜 云南师范大学信息学院本科生.主要研究方向为非刚性点阵配准和医学图像处理.

E-mail:zhfangyu_ynu@163.com

(ZHANG Fang-Yu Undergraduate student at the School of Information Science and Technology,Yunnan Normal University.Her research interest covers non-rigid point set registration and medical imaging.)

Non-rigid Point Set Registration with Mixed Features

TANG Hao-Lin1YANG Yang1,2YANG Kun1,2LUO Yi1,2ZHANG Ya-Ying1ZHANG Fang-Yu1

We present a novel non-rigid point set registration method with mixed features.The proposed method is designed by an alternating two-step process:correspondence estimation and transformation updating.We first design a global and a local feature descriptors for assessing the global and local structural differences between two point sets, respectively.The two feature descriptors are then combined for forming a mixed feature based energy function,so as to provide a flexible way to estimate correspondences by minimizing global or local structural differences using a linear assignment solution.To improve the interactions between the two steps,a tradeoff of energy adjustment is used to gradually adjust the energy minimization from local to global structural differences and the thin plate spline transformation from rigid to non-rigid during registration.We evaluate the performances of our method in contour registration,sequence images and real images;through comparision with other eight state-of-the-art methods,our method shows the best alignments in most deformation and rotation scenarios.

Non-rigid,point set registration,mixed features,correspondence estimation,transformation updating

汤昊林,杨扬,杨昆,罗毅,张雅莹,张芳瑜.基于混合特征的非刚性点阵配准算法.自动化学报,2016,42(11): 1732−1743

Tang Hao-Lin,Yang Yang,Yang Kun,Luo Yi,Zhang Ya-Ying,Zhang Fang-Yu.Non-rigid point set registration with mixed features.Acta Automatica Sinica,2016,42(11):1732−1743

2015-10-10 录用日期2016-05-16

Manuscript received October 10,2015;accepted May 16,2016

国家高技术研究发展计划(863计划)(2012AA121402),云南省教育厅科学研究项目 (2015Z069),云南师范大学博士科研启动基金 (01000205020503065),云南师范大学大学生科研训练基金(0100060502006)资助

Supported by National High Technology Research and Development Program of China(863 Program)(2012AA121402),Key Scientific Research Project of Education Department of Yunnan Province(2015Z069),Doctoral Scientific Research Foundation of Yunnan Normal University(01000205020503065),College Students'Scientific Research Training Project of Yunnan Normal University(0100060502006)

本文责任编委朱军

Recommended by Associate Editor ZHU Jun

1.云南师范大学信息学院昆明650092 2.西部资源环境地理信息技术教育部工程研究中心昆明650092

1.School of Information Science and Technology,Yunnan Normal University,Kunming 650092 2.The Engineering Research Center of GIS Technology in Western China,Kunming 650092

DOI 10.16383/j.aas.2016.c150618