开拓新思路，探究新学法——关于高中数学学习的创新方式研究

江苏省南通市通州区金沙中学(226300)

蒋红雅●



开拓新思路，探究新学法
——关于高中数学学习的创新方式研究

江苏省南通市通州区金沙中学(226300)

蒋红雅●

随着教学理念的不断更新，高中数学的教学内容与教学要求也发生了一定的调整.大趋势的变化也对教学活动的设计提出了要求.我们要顺应教学发展方向，持续创新教学理念与方式，为高中数学课堂提供一种全新的意识氛围，引领学生们在其中更为深刻地感知数学，实现知识能力的有效强化.笔者在教学实践当中以此为目标进行了较长一段时间的尝试，找到了若干行之有效的创新切入点，特在本文当中逐个予以阐述.

一、从预习处创新，做到“超前想”

每一次新知识的学习之前都离不开必要的预习工作.通过预习，学生们可以对即将接触的知识内容形成预先认知，从心理状态与知识能力角度做好准备，以便在正式学习时事半功倍.作为一个重要的铺垫环节，预习工作也就成为了创新性学习的有力开端.如果能够将预习做新、做好，必然可以为整个学习过程增添强大的推动力量.

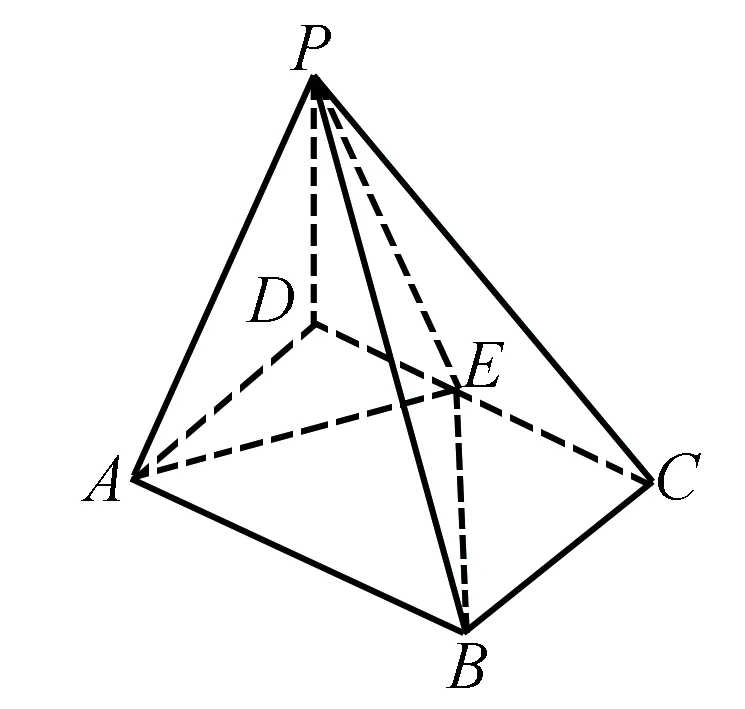
例如，在对立体几何的内容开始学习之前，先为学生们设计了这样一道预习题：如图所示，P-ABCD是一个四棱锥，在它的棱CD上有一个动点E.那么，为了将多面体P-AEB的体积控制为一个恒定值，应当如何确定底面ABCD的面积？如果在还未学习具体知识内容的情况下，要求学生们将最终答案解答出来显然是不适宜的.但是，这个问题也并不是学生们完全无法接近的.通过对这个问题进行思考，学生们很自然地跟随提问对照图形进行了观察与分析，不仅对空间想象能力进行了训练，并从感性上对体积恒定所需要的条件进行了猜想.而在这个猜想的过程当中，学生们为了寻找有力依据，也会很自然地从线面关系的角度展开思考.这也就引出了本次教学的重点.

创新性的数学预习，一定要做到“超前想”，就是要尽可能地将知识学习当中可能会遇到的难点问题提前预见到，并让学生们能够提前接触到、考虑到.这主要是对教师们所提出的要求.在为学生们布置预习任务时，教师们应当有意识地以预习活动作为切入点，让知识重点能够在此环节有所展现.虽然无需学生们过早将之理解掌握，但也应当在正式学习开始之前，对主体知识有感觉、有预知，这样才能在学习活动展开后做到得心应手、游刃有余.

二、从学习处创新，做到“抓典型”

课堂教学是数学学习的核心部分，自然也是创新方式融入的关键环节.对课堂教学进行创新的切入途径有很多，笔者在实践当中比较侧重的方法是“抓典型”，就是通过突出典型知识问题来引起学生关注，并将学习重点加以呈现.抓典型的过程实际上就是一个以点带面的过程，只要抓住了知识学习当中最为有力的一个点，把它学懂学透，其他的边缘性问题也会随之迎刃而解.这种教学方式，既能够大大节约课堂教学时间，还能够收获更有效率的教学效果.

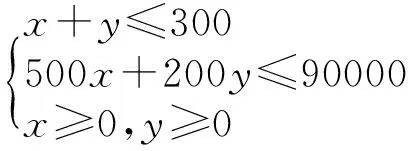
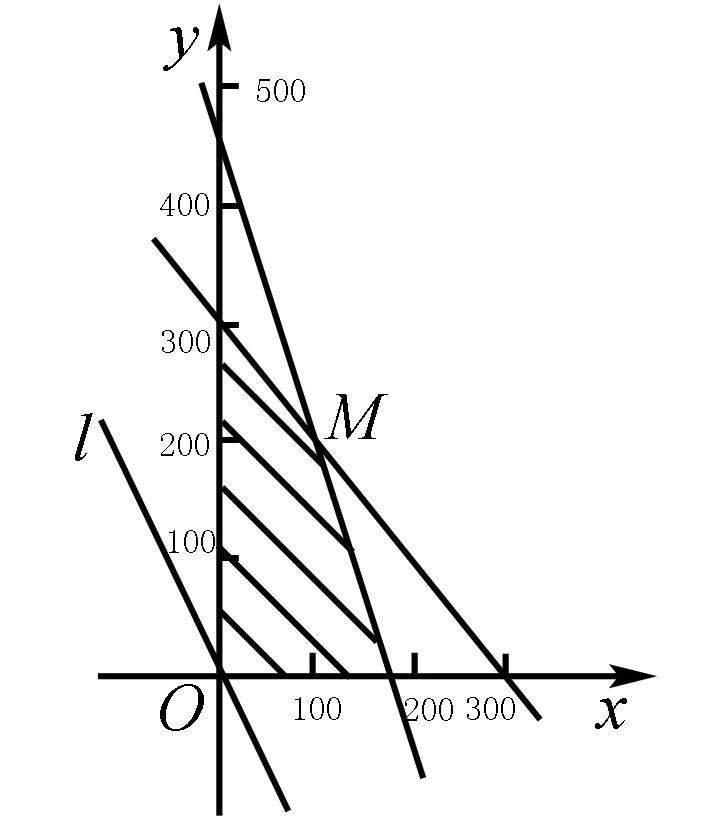
在课堂教学当中，教师们经常会加入例题来呈现知识，这就是“抓典型”做法的开端.从待教学内容当中提炼出精髓的部分融于问题加以提出，便可以让学生们在解答问题的同时意识到知识内容的重点所在，并在典型问题所引导的路径上深化思考，无需教师过多提出硬性要求，同样可以让学生们明确学习要求，找准努力方向.

三、从复习处创新，做到“找方法”

对于数学知识来讲，一次的学习总是不够的.特别是高中数学丰富灵活的学科特点决定了，每个知识模块的学习告一段落之后，都要进行必要的复习，在总结所学的同时，还能够发现新的探究入口，将学习效果推向深入.由此，复习环节也就很自然地成为了教学创新的另一个关键抓手.想要完成高质、高效的复习，仅凭增加时间与精力成本是远远不够的，最重要的是要找到合理有效的方法.

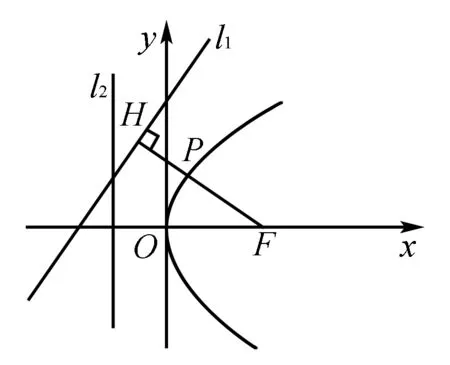
例如，在带领学生们学习过解析几何的内容后，可请学生们以这样一道习题进行复习：现有两条直线分别为l1：4x-3y+6=0，l2：x=-1，且有一条方程式为y2=4x的抛物线.若在该抛物线上有一个动点P，那么，该动点到上述两条直线的距离之和能够取得的最小值是多少？对于这个问题，应当如何快速准确地进行解答呢？停留在文字表面逐个开始计算吗？

当然不是.经过将题目条件以图形的方式表示出来之后(如图)，学生们很轻松地发现，当图中的F、P、H三点共线时能够取得最小值.在这个分析过程中，具体的推导并不是最重要的，而是借助图形分析问题的思想方法，即数形结合.

通过把握方法来进行复习，对于高中数学学习来讲具有两个方面的积极意义：第一，方法就像是一个通行性的工具，掌握了方法，便可以根据具体问题的种类来加以适用，简化解题过程，提高分析质量.第二，对于具体知识内容来讲，方法是数学学习的一种升华.如果学生们能够在复习过程当中将思想方法提炼出来，便可以将整个学习效果顺利推到一个新的高度.如此一举两得的效果，我们何乐而不为呢？

四、从作业处创新，做到“重实践”

作为某一次知识学习的尾声，课后作业总是必不可少的.随着素质教育的要求不断深入，对于作业布置数量的限制愈发严格.为了能够始终保证作业的自身质量与达成效果，就要从作业内容的代表性与精炼性入手加以创新，使之在较小数量的前提之下达到更高的训练实效.那么，如何才能有效强化课后作业的质量呢？笔者认为，“重实践”是一个不可或缺的考量因素.

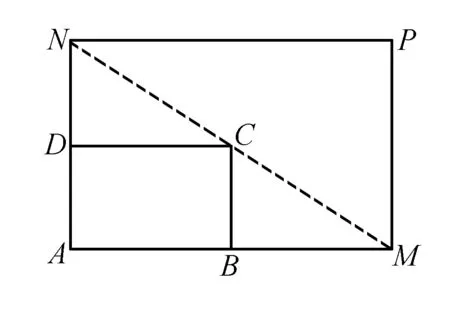
例如，我曾经在分式函数的课后作业中设计了这样一道习题：如图所示，现有一个街心公园ABCD，欲将之扩建为AMPN，二者均是矩形，且点M和点N分别在AB和AD的延长线上，点C在对角线MN上.若AB长为3米，AD长为2米，设AN长为x米，且3≤x<4，那么，为了让扩建后的面积最大，AM和AN的长度需要取得多少？当分式函数的理论知识与实际问题联系起来之后，该理论知识的范围被扩展了不少.通过这个实践过程，也加深了大家对于分式函数的理解.

表面看来，数学学科的理论性是很强的，这也导致很多学生误以为这就是数学学习的全部.笔者通过对作业内容开展广泛调查也发现，单纯的理论性内容也几乎占据了课后作业的全部.这种作业布置导向是存在着较大偏颇的.高中数学学习之中，不仅有理论，实践的内容也有很多.作为对理论知识学习的检验，对于实践的关注必不可少.这种意识也应当通过作业布置予以体现.与此同时，如果能够让学生们在完成作业的同时感受到学以致用的感觉，对于提升大家的学习热情也是助益颇多的.

从本文当中的叙述不难发现，笔者所采取的教学创新是按照教学开展的时间顺序来逐阶段进行的.从预习到课堂教学，再到课后复习，直至作业练习，每一个教学环节之中都是存在着很大的创新空间的.教师们需要做的是，首先发现创新机会之所在，然后结合当前所需开展教学的内容特点与学生们的实际需求，设计选择最为合理且高效的教学方式及活动.经过全方位、多角度的创新渗透，学生们对于高中数学知识学习的热情大增，学习效果也得到了切实提升，真正实现了教学实效的“双收获”.

G632

B

1008-0333(2016)31-0036-02