基于数形结合在高中数学中的应用解析

江苏省靖江市斜桥中学(214500)

杨正辉●



基于数形结合在高中数学中的应用解析

江苏省靖江市斜桥中学(214500)

杨正辉●

一、集合问题中数形结合思想的应用

对于集合的交、并、补等运算，往往都是采取集合运算中的数轴、韦恩图进行计算，通过这样的方式能使得题型简化，从而将运算方式简洁.

例1 已知集合A=[0,4],B=[-2,3],求A∩B.

解析 针对这两个集合，可以在数轴上将其表示出来，那么，久能够很明确的知道结果.

如图1所示，我们很容易就看出A∩B=[0,3].

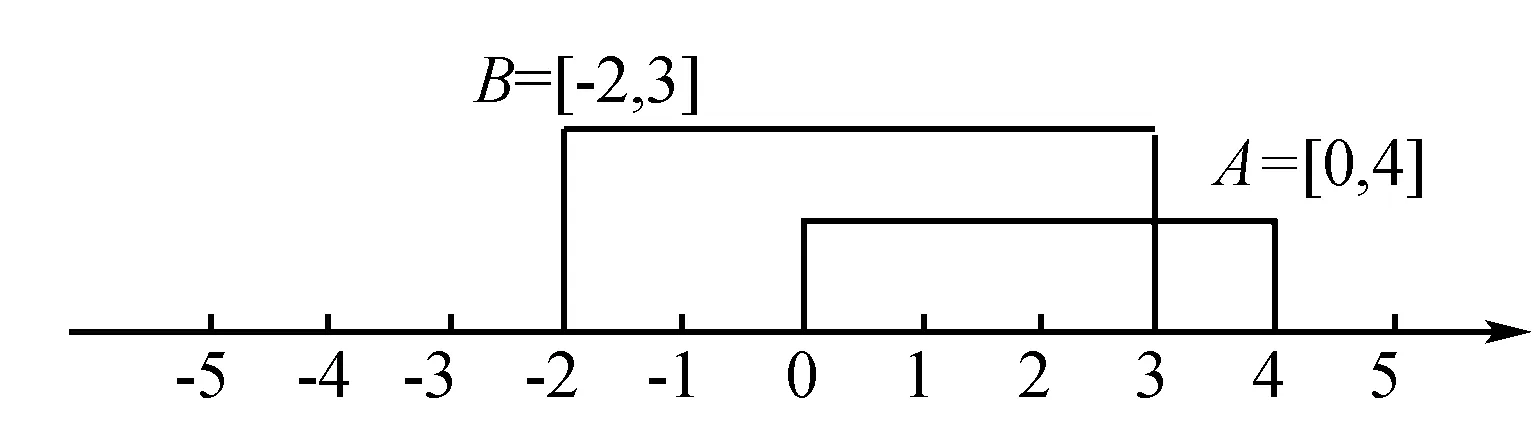
图1

二、函数中属性集合思想的运用

在高中数学教学中，函数是非常重要的一部分内容，它在教学中的作用于地位高于其他方式，而数形结合思想在进行解题时所发挥的效果也非常重要.

例2 函数f(x)是定于R上的偶函数，在(-∞，0]上是减函数，并且f(2)=0，那么不等式f(x)<0的解是____.

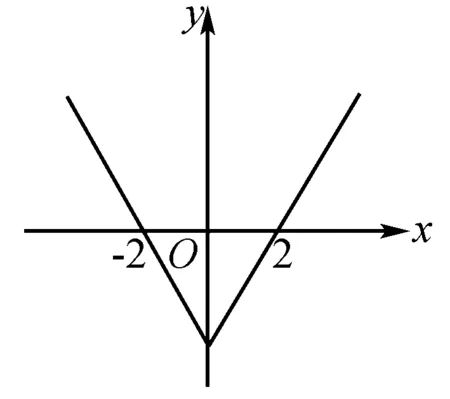
图2

解析 结合题设条件画示意图图2可知，f(x)<0的解集是(-2，2) .

三、通过使用数形结合求三角函数最值

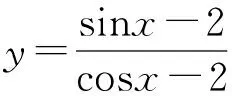
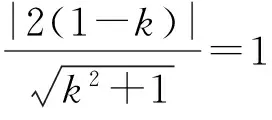
四、复数中数形结合的应用

例4 设z∈C，并且|z|≤1/2，求|z+1|的取值范围.

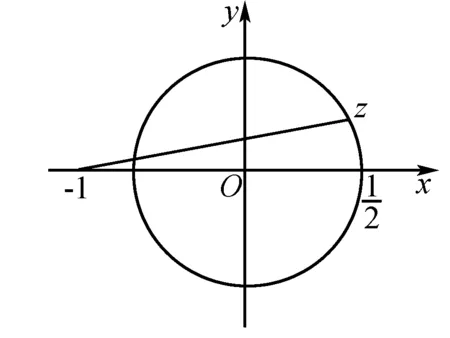
图3

解 |z|≤1/2，表示以原点为圆心，半径为1/2的圆及其内部，|x+1|表示点Z与点-1之间的距离.由图3可见1/2≤|x+1|≤3/2.

五、几何问题中数形结合的应用

A.1个 B.2个 C.3个 D.4个

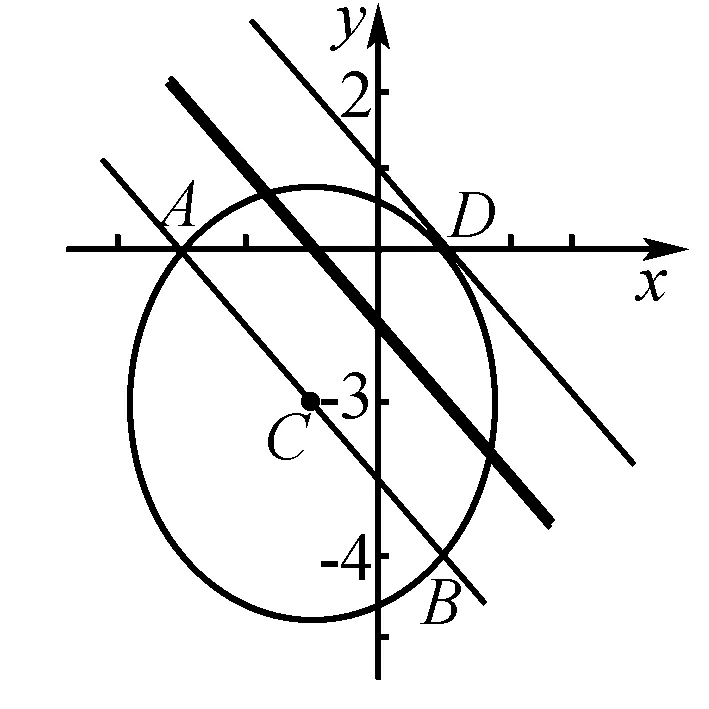
图4

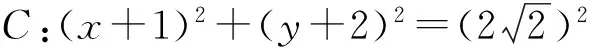
由以上实例分析可知，通过利用图形结合的方式，能够将难解的题型简化为容易分析的题型，能够轻松将求解的问题得出，因此，想要贯通这些数形结合思想，在解题过程中需要重视以下方面内容：

(1)对于题型的图形我们要善于观察，对其中包含的数量关系一定要认知；

(2)需要学会绘制图形，需要能清晰地将图形中相应的数量关系表示出来；

(3)能够掌握数与形两者之间的相互关系，从而能够将形转变成数，能够将数转换成形；

(4)要做好应用数以及形之间的互化，将创造性以及灵活性思维提升.

总而言之，想要让学生能够掌握好数形结合思想的核心，那么就需要使得学生能够有扎实的基础，只有这样，才能够使得数形结合得到有效运用，进而能够提升学生们的解题能力.

G632

B

1008-0333(2016)31-0047-01