例说巧用数学思想解决圆锥曲线综合问题

安徽省利辛高级中学(236700)

陈国林●

江西赣南师范大学科技学院(341000)

寇桂宴●



例说巧用数学思想解决圆锥曲线综合问题

安徽省利辛高级中学(236700)

陈国林●

江西赣南师范大学科技学院(341000)

寇桂宴●

数学思想是解决数学问题不可忽视的一部分内容，在解决圆锥曲线问题时，由于其运算量比较大,而且容易出现计算上的错误,如果在求解问题时能够充分地利用数学思想方法,可以减少运算量,因此同学们在掌握其基础知识的同时,还应注意数学思想的提炼、总结．下面举例介绍,供大家参考．

一、1.数形结合思想

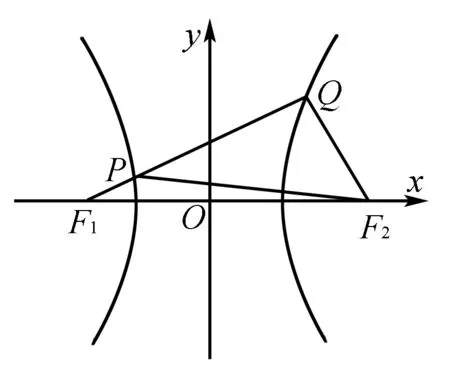
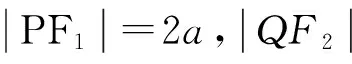
答案:A.

点评 本题考查了余弦定理和双曲线的定义和几何性质.在几何问题的求解中例如离心率、最值问题和取值范围问题，如果能画出图形并结合图形上点的条件进行观察转化，能够帮助你快速求解题目.

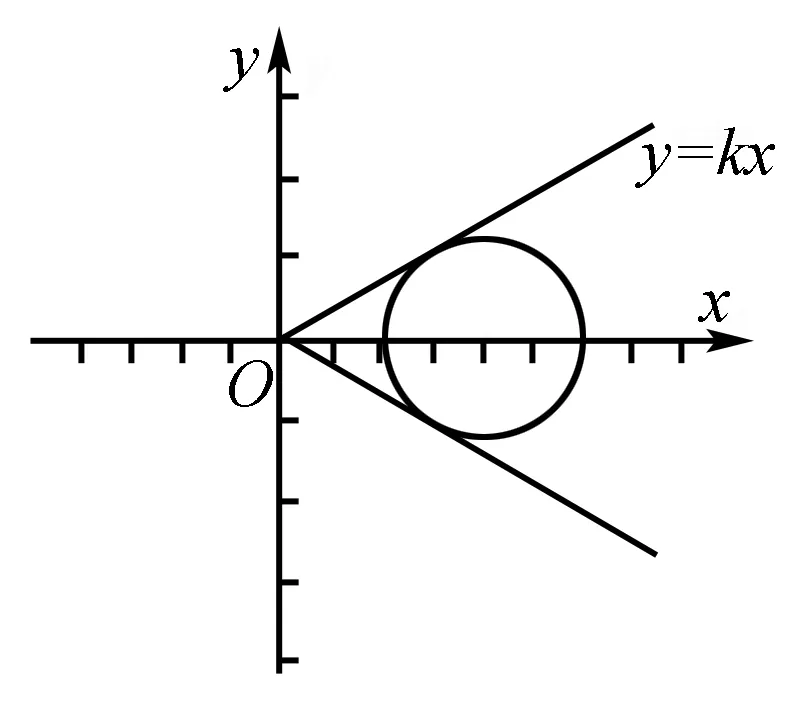
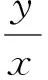
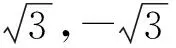
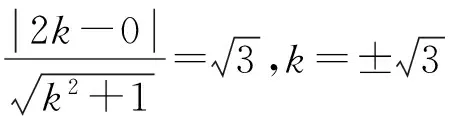
二、分类讨论思想

例2 (2016年浙江省绍兴市高三质检)已知点M(2,1)及圆x2+y2=4，则过点M的圆的切线方程为____.

分析 当切线斜率不存在时，显然x=2成立，当斜率存在时，设斜率为k，利用点到直线间的距离公式d=r列出关于k的方程，解之即可求出.

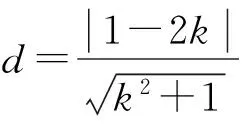
综上可知，切线的方程为x=2或3x+4y-10=0.

点评 本题考查圆的方程和直线与圆间的位置关系．对于直线方程，根据斜率存在与否是本题产生讨论的原因．

(1)求椭圆C的方程；

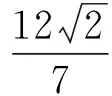
又a2=b2+c2，解得a2=4，b2=3，

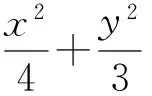
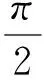
三、函数与方程思想

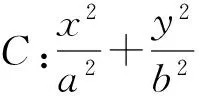
(1)求椭圆C的标准方程;

(2)设点A，B分别是椭圆C的左、右顶点，过点(1,0)的直线l与椭圆交于M，N两点(M，N与A，B不重合),证明：直线AM和直线BN交点的横坐标为定值.

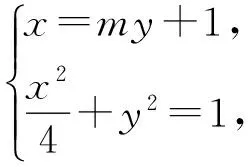
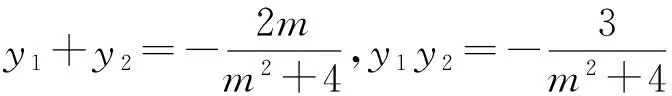
点评 解析几何中的许多问题都需要利用方程思想去解决，例如求定值问题、直线和二次曲线的位置关系问题等等，都需要联立方程通过解二元方程组才能解决，涉及到二次方程与二次函数的有关理论需要建立函数关系或构造函数，一般可以运用函数的图象和性质去分析问题、转化问题使问题获得解决.

四、化归与转化思想

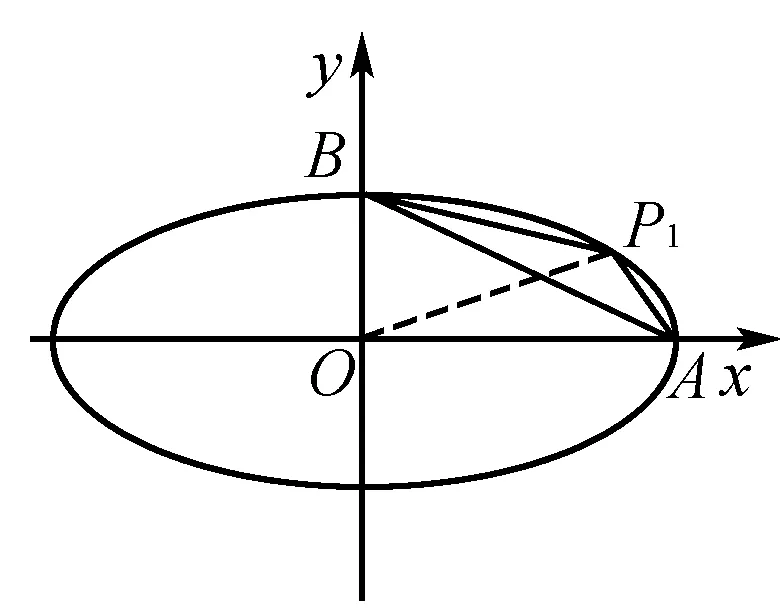
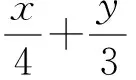
分析 设出P1的坐标，表示出四边形P1AOB的面积S，利用两角和公式整理后，利用三角函数的性质求得面积的最大值，进而求得△P1AB的最大值，利用最大值判断出点P的位置.

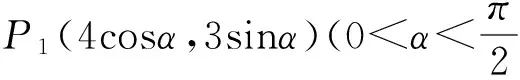
答案:2

点评 化归与转化思想是解析几何中最常用的数学思想之一，在解决解析几何问题中如果遇到一些难处理的问题，如果将问题转化到其它问题上求解会更易处理，比如点的个数，最值问题等.

G632

B

1008-0333(2016)31-0008-02