点差法的改进
——2015年高考浙江理19另解
2016-12-16云南省蒙自市蒙自一中凤凰校区661100
数理化解题研究 2016年31期
云南省蒙自市蒙自一中凤凰校区(661100)
朱东海●
点差法的改进
——2015年高考浙江理19另解
云南省蒙自市蒙自一中凤凰校区(661100)
朱东海●
在2015年理科高考数学试卷中,有安徽、全国(Ⅱ)、陕西和浙江卷中出现了弦中点问题.弦中点问题一般可用点差法来解决,也就是说,若直线l与曲线C交于A、B两点,就可以设A(x1,y1),B(x2,y2),然后把A、B两点的坐标代入曲线C的方程中,两式相减,再按照题目的要求来处理.本文以2015年高考浙江理19为例,对点差法进行改进,同时给出该题的另一种解法

(1)求实数m的取值范围;
(2)求△AOB面积的最大值(O为坐标原点).
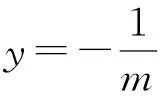

另解:(1)设AB的中点为M(x0,y0),A(x0+t1,y0+t2),B(x0-t1,y0-t2),由题意知m≠0,


①-②得:x0t1+2y0t2=0.


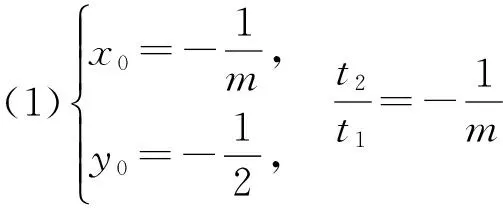
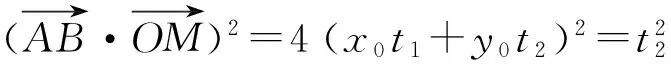


对点差法的改进是,若直线l与曲线C交于A、B两点,利用对称性,设AB的中点为M(x0,y0),A(x0+t1,y0+t2),B(x0-t1,y0-t2),然后把A、B两点的坐标代入曲线C的方程中,两式相减,再按照题目的要求来处理,可以使问题得到简化.
G632
B
1008-0333(2016)31-0019-01
