构造向量求解几类根式的最值问题

江苏省常熟市尚湖高级中学(215500)

马怡平●



构造向量求解几类根式的最值问题

江苏省常熟市尚湖高级中学(215500)

马怡平●

求含两个根式和(差)的最值问题，按常规方法不易求解.如果能由式子的特征构造出相应的向量，再恰当运用向量不等式|a|-|b|≤|a±b|≤|a|+|b|,或|a·b|≤|a||b|来解答，既可开僻新的解题途径，又可使解答更为简捷.本文就几类常见的根式类最值问题，举例说明.

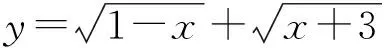
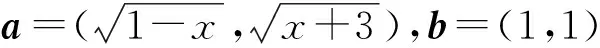
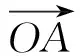
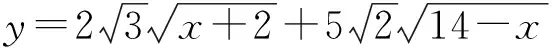
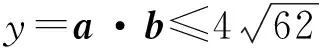
点评 本例中两个根号中的x的系数不是相反数，为了使所构造的向量b满足|b|是常数，需要对各根式的系数适当搭配，这是求解中的难点，应特别关注.

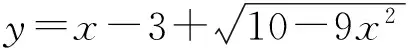
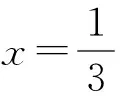
点评 所设的a和b，一方面有y=a·b+c,另一方面应满足|a|和|b|都是常数，因此要结合根号中的式子，对根号外式子的系数进行适当的配凑.这是求解这种类型函数最值的关键所在.我们再看一例，加以体会.

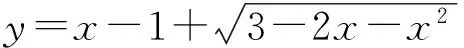
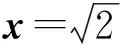
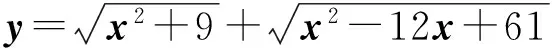
点评 本例是两个根式和的形式，所构造的两个向量a与b要满足两个条件；

(1)a+b是常向量；(2)a与b应同向.

这样才能保证|a|+|b|≥|a+b|中取到等号并得到最小值.

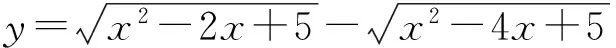
点评 对两个根式的差的形式，在构造向量a、b时要注意：

(1)使a+b是常向量；(2)在|a|-|b|≤|a+b|中取等号的条件是a与b反向.当然了，如果运用|a|-|b|≤|a-b|取等号条件，那么应使a-b是常向量且a与b同向.

G632

B

1008-0333(2016)31-0048-01