贝叶斯冲突Web数据可信度算法

王继奎

(兰州财经大学 电子商务综合重点实验室,甘肃 兰州 730020)



贝叶斯冲突Web数据可信度算法

王继奎

(兰州财经大学 电子商务综合重点实验室,甘肃 兰州 730020)

Web数据融合的关键是判定冲突Web数据的可信度.已有算法只采用观察值之间的相似关系而忽视包含关系对可信度进行修正,针对这一问题,在分析观察值本身特性的基础上定义观察值包含度,提出利用观察值包含度对观察值可信度进行修正的模型.将观察值看作随机变量,观察值的可信度问题可归结为观察值的后验概率分布问题.在贝叶斯分析的基础上,定义数据源可信度,推导出数据源可信度与观察值可信度之间的关系模型；并提出基于贝叶斯理论的冲突Web数据可信度算法DataCredibility.实验结果表明,与基准算法相比,DataCredibility获得了更高的精确度、召回率及F1测度值.

冲突Web 数据; 贝叶斯理论; 可信度；数据融合; DataCredibility

随着互联网技术的飞速发展,Web已经成为一个巨大的、分布广泛的和全球化的信息中心[1].目前整个Web有超过200 000TB的信息量,而且仍在快速地增长[2].2004年4月,UIUC大学推测出整个Web上大约有45.0万个Web数据库以及30.7万个有数据库的站点[3].依据文献[4]的调查,美国的消费者对网上信息的信任度很低,甚至连可信度最高的网上资源、公司网站也仅有22%的美国人信任.Dalvi等[5]研究了Web上数据的冗余问题,但是没有考虑数据的一致性问题.Li等[6]对股票与机票两个领域的数据一致性进行了研究,结果表明：70%的实体有不止一个值,大部分是由于各种歧义造成的；而其中的30%看起来是完全错误的.

如何确定Web数据的可信度成为研究的焦点问题,研究者针对这一问题进行了大量的研究.Yin等[7]首次将从多个冲突值中选择一个作为真值的冲突解决策略称为真值发现问题,并提出基准算法TruthFinder,观察值的可信度取决于其相关数据源的可信度,而数据源的可信度取决于其提供的观察值的可信度,利用两者关系迭代计算,直到算法收敛,或者达到迭代次数阈值.同时,TruthFinder也考虑了观察值之间的相似关系,并通过观察值之间的相似关系修正观察值的可信度.Galland等[8]在TruthFinder的基础上提出了Cosine、2-Estimates和3-Estimates算法、NormalizedSources算法.Cosine算法利用观察值与真值之间的余弦相似度度量观察值的可信度,将观察值的数据源的平均可信度作为观察值的可信度,将可信度最高的作为真值.2-Estimates和3-Estimates算法使用了数据源的错误率与观察值的真值2个估计器,2-Estimates迭代地计算了真值的可信度以及数据源提供错误观察值的概率.真值的可信度通过提供真值的数据源的可信度(1-错误率)计算.3-Estimates算法在2-Estimates的基础上考虑了观察值的获取难度.NormalizedSources算法则考虑了数据源提供观察值数量的情况.Pasternack等[9]提出了一个考虑先验概率的真值发现算法框架.Jøsang等[10]研究了数据源信任传播的机制.张志强等[11]在文献[7]的基础上改进了数据源权威度评价方法.张永新等[12]根据所有观察值的离散程度分两阶段处理.Zhao等[13]基于贝叶斯理论提出了将真值发现问题归结为参数估计问题,提出了一种多真值发现算法.Ravali等[14]考虑了数据源的相关性,并将之应用在真值发现中.Li等[15]提出了一种基于数据源可信度置信区间的真值发现算法.这些工作主要从数据源与观察值之间的结构关系进行研究,对于观察值之间的关系研究甚少.

针对已有算法只采用观察值之间相似关系而忽视包含关系对可信度进行修正这一问题,本文利用数据源精确度定义数据源可信度,推导出数据源可信度与观察值可信度之间的关系模型；定义观察值包含度,提出利用观察值包含度对观察值可信度进行修正的模型,在此基础上提出基于贝叶斯的冲突Web数据可信度算法DataCredibility,并在通用数据集Books-Authors上进行实验.

1 数据可信度问题的定义

为简化讨论,假设实体只有1个属性,并假设只有1个属性真值.

令W={w1,w2,…,wn},W表示数据源集合,用i表示标号为i的数据源.

令E={o1,o2,…,ol},E表示观察的集合,oj,j∈[1,l]表示标号为j的观察,用v(oj)表示观察值,e(v(oj))表示被观察对象,s(oj)表示提供观察oj的数据源.

设离散随机变量X∈{x1,x2,…,xn}代表可能观察值,其中有1个真值,n-1个错误值.p(X=x)表示X在取值空间上的先验概率分布.

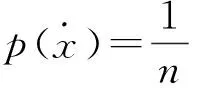
(1)

假设数据源提供不同错误观察值的概率符合均匀分布,则

(2)

式中：a为数据源的精确度,用数据源提供观察值v(o)=x的条件概率表示.

同时,数据源的精确度也可以用其提供的观察值为真值的概率的算术平均值表示,即

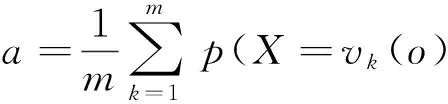
(3)

式中：m为数据源提供的观察值个数,vk(o)为数据源提供的第k个观察值.

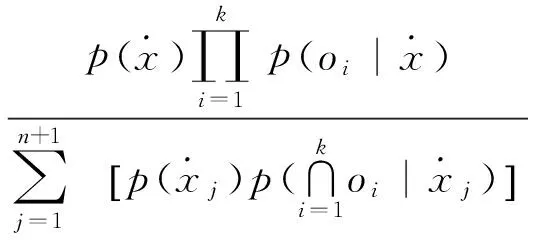
(4)

由于各数据源独立提供观察值,可得

(5)

式中：Wo(x)为观察值为x的数据源集合,Wo为所有提供观察值的数据源集合.

由贝叶斯公式及式(1)、(2)、(5)可得

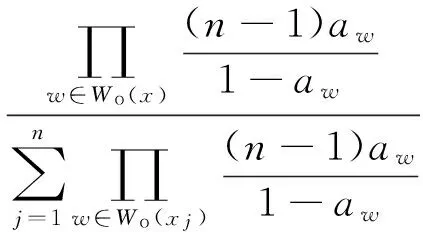
(6)

因此,

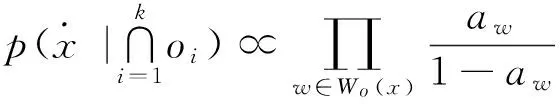
定义1 数据源的可信度：

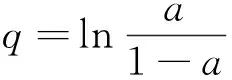
(7)

式中：q为数据源可信度,即q由数据源提供真值的概率与提供错误值的概率的比值决定.

1)当a=0.5时,数据源未提供有利于判断真值的观察值,则q=0.即一个人说的话正确与错误的概率相等,那么这个人就没有任何可信度,其提供的证据也没有任何价值.

2)当a>0.5时,数据源提供真值的概率大于提供错误值的概率,则q>0.即一个人说真话的概率大于说假话的概率,那么这个人说的话就有一定的可信度,说真话的概率越大,则说假话的概率越小,可信度越大.

3)当a<0.5时,数据源提供真值的概率小于提供错误值的概率,则q<0.即一个人说假话的概率大于说真话的概率,那么这个人说的话就有负的可信度,说假话的概率越大,则说真话的概率越小,可信度也就越小.

由于a∈[0,1],实现时为了避免a接近0或1的时候q过小或过大,对q的计算进行修正,则

(8)

式中：ε取0.1左右的值.

定义2 观察值x的可信度c(x)

由于

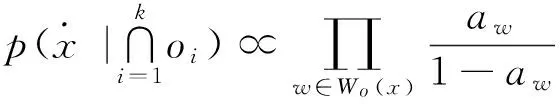
令

则

(9)

即c(x)由提供观察值x的数据源的可信度决定.后验概率分布p(X=x)∝c(x),令

(10)

对同一实体的观察值的可信度归一化,归一化后的结果即为观察值为真的后验概率.其中∑o(y)=o(x)c(y)为归一化因子.

2 观察值包含度

观察值的可信度不仅取决于数据源的可信度,也与观察值之间的关系有关.文献[6]采用了观察值之间的相似关系对观察值的可信度进行了修正.然而数据之间的关系不只是相似关系,在Web世界中,大量存在对同一客观实体正确但不完全的观察值,观察值之间存在包含关系.

2.1 观察值包含度

定义3 包含度[16]

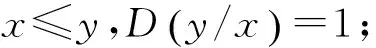
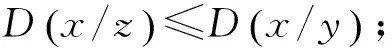
上述定义中：1)是对包含度的规范化.2)是包含度与经典包含的协调性,经典包含仅是包含度为1的特殊情况.3)与4)是包含度的单调性.

设F为一个字符串集合,di,dj∈F,设si与sj分别为字符串di,dj的词项集合,若si⊆sj,则称dj包含di,用didj表示,为二元运算符.由偏序集定义可知,(F,)为偏序集.

定义5 偏序集(F,)上的包含度

(11)

2.2 观察值包含度计算

设s1(bi),s2(bj)分别表示描述d1,d2的词项集合s1,s2中的元素；m,n代表s1,s2中包含的词项个数,n≠0.描述包含度的计算公式为

D(d1/d2)=

(12)

2.3 包含度对观察值可信度的修正

综合考虑数据源的可信度以及观察值之间的包含度,修正后观察值的可信度c′(x)如下：

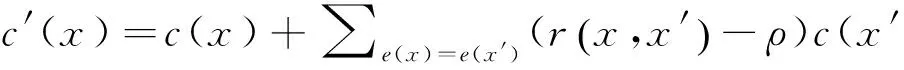
(13)

式中：ρ为包含度阈值,即当包含度大于某一阈值时；做正修正；小于某一阈值时,做负修正.

在DataCredibility算法实现中ρ=1,即如果观察值不能包含被观察值,则被观察值对观察值作负修正.与基于相似度的修正不同,基于包含度的修正是非对称的.

3 数据可信度算法

在未知数据源精确度的先验概率的情况下,统一赋予每个数据源相同的初始精确度a0>0.5.

3.1 算法流程

令A=[a1,a2,…,an]表示数据源精确度向量,Q=[q1,q2,…,qn]表示数据源可信度向量,V=[v1,v2,…,vk]表示观察值向量,C=[c1,c2,…,ck]和C′=[c′1,c′2,…,c′k]分别表示修正前和修正后的观察值可信度向量,M表示数据源与观察值之间的关联矩阵矩阵：

(14)

将数据源集合W和观察值向量V看作顶点,将关联矩阵Mk×n看作边,则G(W∪V,M)是一个二部图.矩阵M包含二部图的结构信息.

令R表示观察值包含度矩阵：

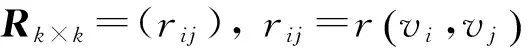
(15)

R蕴涵了观察值之间的包含度信息.

由式(10)得

C=MQ.

(16)

由式(14)得

C′=RC.

(17)

DataCredibility算法的流程如下：

输入：W、A、M、精确度初始值a0、迭代次数阈值t、收敛阈值λ=10-5

Begin

计算包含度矩阵R∥利用式(13)计算包含度矩阵

for allwi∈W∥给所有数据源赋精确度初始值a0

ai=a0

Repeat ∥迭代计算

for allqj∈Q∥计算所有数据源质量

ifaj>0.5

else ifaj<0.5

C←MQ∥利用式(17)计算修正前的观察值可信度向量

C′←RC∥利用式(18)计算修正后的观察值可信度向量

C←C′∥保存观察值可信度向量中间结果}

根据式(3)计算A

Until 迭代次数大于t或A的变化小于λ

输出C,A∥可信度最大的观察值判断为真值

end

3.2 算法复杂度

设数据源集合W的有i个元素,观察值V向量有m个元素.因为数据源的个数往往比其提供的观察值的个数小的多,通常m远大于i.包含度矩阵R的计算取决于实体个数与每个实体的冲突观察值个数.设每个实体平均有k个观察值,则每个观察值与其他k-1个观察值冲突.计算矩阵R的时间复杂度为m/k×k×(k-1),表示为O(mk)；计算向量C的时间复杂度为i×m,表示为O(im),计算向量C′计算的时间复杂度为O(ik2),即O(mk).考虑到算法的迭代实现,设迭代次数为t,则DataCredibility算法的时间复杂度为O(mk+tmk).由于m远大于k、t,DataCredibility算法对观察值个数m有近似线性的时间复杂度.算法的空间复杂度也为O(m).

4 实验结果及分析

实验对比算法为2-Estimates[8]、3-Estimates[8]、NormalizedSources[8]、TruthFinder[7].

实验采用以下指标度量算法的有效性.

1)精确度p、召回率r、F1测度：精确度p度量了算法正确判定为真值的比例；召回率r度量了算法正确判定为真值的观察值占所有真值的比例；F1测度综合考虑了上述2者的结果,由下式计算:

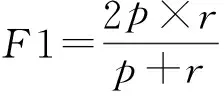
(18)

2)精确度回归曲线：从1个观察值开始,每次增加1个观察值,并计算各算法精确度p和召回率r,将r作为x坐标,p作为y坐标,绘制散点图.利用曲线下的面积作为衡量算法有效性的指标.

4.1 真实数据集

实验采用Books-Authors数据集[17],包括1 265本计算机科学与工程相关的书籍,895个数据源以及33 971个条目.真值通过查看书籍封面获得.

实验选取数据集Books-Authors中给定真值的100本书对应的观察值进行实验，其中包含237个数据源,共有2 455个观察,651个观察值,有85个真值.将数据集中的作者列表信息利用分词工具分割成多个词项.比如将“hoos,holger h.;stutzle, thomas”分割成2条描述“hoos,holger h.”与“stutzle, thomas”.

4.2 精确度p、召回率r和F1测度指标对比

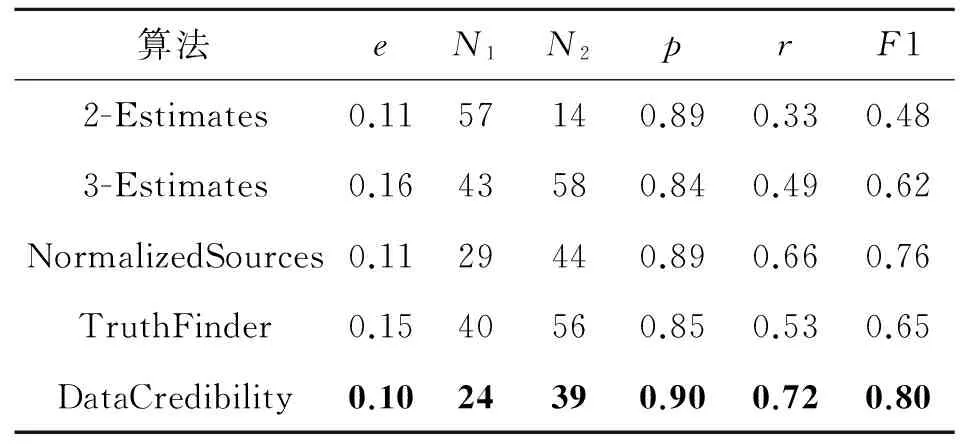
为了使结果具有可比性,采取了与文献[6]相同的运行参数.实验运行参数设置为初始精确度a0=0.8,迭代次数阈值为10,ε=0.1,包含度阈值ρ=1,收敛阈值λ=10-5.DataCredibility算法与以及2-Estimates、3-Estimates、TruthFinder、NormalizedSources算法在错误率e、弃真数量N1、取伪数量N2、精确度p、召回率r和F1测度指标上的性能如表1所示,其中最优结果用加粗字体表示.

表1 各算法在6个指标上的性能对比

Tab.1 Performance comparison of algorithms on six indicators

算法eN1N2prF12-Estimates0.1157140.890.330.483-Estimates0.1643580.840.490.62NormalizedSources0.1129440.890.660.76TruthFinder0.1540560.850.530.65DataCredibility0.1024390.900.720.80

由表1可知,算法DataCredibility 的p、r、F1分别为0.90、0.72、0.80均为最好.DataCredibility算法与NormalizedSources算法的有效性最接近,与其相比F1提高了4%,r提高了6%,p提高了1%.这验证了采用新的数据源可信性度量方式并使用包含度进行观察值的可信度修正能够显著提高算法的有效性.

4.3 精确度回归曲线

利用召回率r作为横坐标,精确度p作为纵坐标,绘制精确度回归曲线图.利用精确度回归曲线下的面积作为衡量各真值发现算法的有效性.实验运行参数设置与4.2节相同.如图1所示为根据实验数据绘制的精确度回归曲线图.

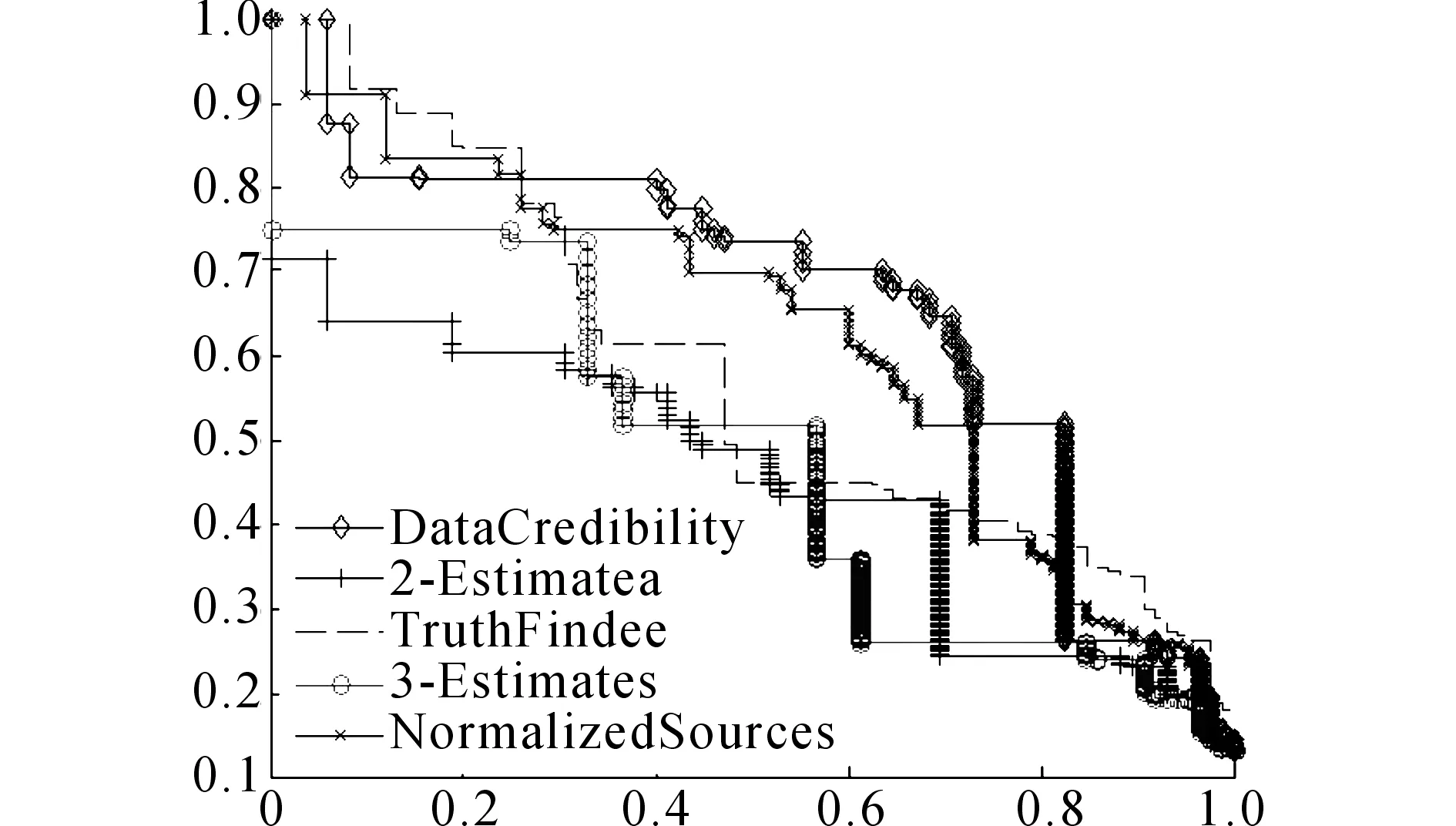
图1 不同算法对应的精确度回归曲线Fig.1 Precision recall curves of different algorithms

由图1可得,算法TruthFinder、3-Estimates、2-Estimates、NormalizedSources对应的曲线面积分别为0.45、0.58、0.48、0.62；而DataCredibility算法对应的曲线面积为0.66,相比于前4种算法分别提高了46.7%、13.8%、37.5%、6.45%.这验证了算法DataCredibility的有效性.

5 结 语

与现有TruthFinder、3-Estimates、2-Estimates、NormalizedSources算法相比,本文提出的DataCredibility算法在精确度、召回率、F1测度3个度量指标方面均获得了较好结果,验证了算法的有效性.这对于Web场景下观察值之间包含等不对称关系的可信度度量很有价值.

DataCredibility算法适用于字符型数据,对数字、日期等类型数据不适用；该算法与TruthFinder等迭代算法一样,对数据源初始可信度值敏感；同时,该算法没有考虑数据融合中的数据动态变化特性,这些问题有待进一步研究.

[1] 董永权.Deep Web数据集成关键问题研究 [D]. 济南：山东大学, 2010. DONG Yong-quan. Key problem of deep web data integration [D]. Jinan: Shandong University, 2010.

[2] FETTERLY D, MANASSE M, NAJORK M, et al. A large-scale study of the evolution of web pages [C] ∥ In proceedings of the 12th international conference on World Wide Web. Budapest: ACM, 2003: 669-678.

[3] CHANG K C C, HE B, LI C, et al. Structured databases on the web: observations and implications [J]. ACM Sigmod Record, 2004, 33(3): 61-70.

[4] ENRIGHT A. Consumers trust information found online less than offline messages [J]. Internet Retailer, 2010, 25.

[5] DALVI N, MACHANAVAJJHALA A, PANG B. An analysis of structured data on the web [C] ∥ In proceedings of the 38th International Conference on Very Large DataBases. Istanbul: ACM, 2012: 680-691.

[6] LI X, DONG X L, LYONS K, et al. Truth finding on the deep web: Is the problem solved？ [C] ∥ In proceedings of the 38th International Conference on Very Large DataBases. Istanbul: ACM, 2012: 97-108.

[7] YIN X X, HAN J W, YU P S. Truth discovery with multiple conflicting information providers on the Web [J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(6): 796-808.

[8] GALLAND A, ABITEBOUL S, MARIAN A, et al. Corroborating information from disagreeing views [C] ∥ In proceedings of the third ACM international conference on Web search and data mining. New York: ACM, 2010: 131-140.

[9] PASTERNACK J, ROTH D. Knowing what to believe (when you already know something) [C] ∥ In proceedings of the International Conference on Computational Linguistics. Beijing: ACM, 2010: 877-885.

[10] JØSANG A, MARSH S, POPE S. Exploring different types of trust propagation [C] ∥ International Conference on Trust Management. Berlin Heidelberg: Springer, 2006: 179-192.

[11] 张志强,刘丽霞,谢晓芹,等.基于数据源依赖关系的信息评价方法研究[J].计算机学报, 2012, 35(11):2392-2402. ZHANG Zhi-qiang, LIU Li-xia, XIE Xiao-qin, et al. Information evaluation based on source dependence [J]. Chinese Journal of Computers, 2012, 35(11): 2392-2402.

[12] 张永新,李庆忠,彭朝晖.基于Markov逻辑网的两阶段数据冲突解决方法 [J]. 计算机学报, 2012, 35(1): 101-111. ZHANG Yong-xin, LI Qing-zhong, PENG Zhao-hui. 2-stage data conflict resolution based on Markov logic networks [J]. Chinese Journal of Computers, 2012, 35(1): 101-111.

[13] ZHAO B, RUBINSTEIN B I, GEMMELL J, et al. A bayesian approach to discovering truth from conflicting sources for data integration [C] ∥ In proceedings of the 38th International Conference on Very Large DataBases. Istanbul: ACM, 2012, 5(6): 550-561.

[14] RAVALI P, ANISH D S, DSONG X L, et al. Fusing data with correlations [C] ∥ In proceedings of the SIGMOD, Snowbird: ACM, 2014: 433-444.

[15] LI Q, LI Y, GAO J, et al. A confidence-aware approach for truth discovery on long-tail data [C] ∥ In proceedings of the 41th International Conference on Very LargeDataBases. Kohala Coast: ACM, 2015: 425-436.

[16] 曲开社,翟岩慧.偏序集,包含度与形式概念分析[J].计算机学报,2006,29(2): 219-226. QU Kai-she, ZHAI Yan-hui. Posets, inclusion degree theory and FCA [J]. Chinese Journal of Computers, 2006.29(2): 219-226.

[17] YIN X, DONG L. Data sets for data fusion experiments (III. Book) [EB/OL]. (2012-12-07) [2015-10-01]. http:∥lunadong.com/ fusionDataSets.htm.

Bayesian conflicting Web data credibility algorithm

WANG Ji-kui

(KeyLaboratoryofelectroniccommerce,LanzhouUniversityofFinanceandEconomics,Lanzhou730000,China)

The key of Web data fusion is to judge the credibility of conflicting Web data. The credibility of observing values was only rectified by their similarity relations, while the inclusion relations was ignored in existed algorithms. To solve this problem, the concept of inclusion degree was defined based on the characteristic analysis of the observing values; a modified model was proposed to rectify the credibility of observing values using inclusion degree was proposed. Taking the observing values as random variables, the reliability problem of the observation values could be attributed to a posterior probability distribution problem. Bayesian theory was adopted to define the conception of data source credibility, to derive the relationship model for data source credibility and observing value credibility, and to propose the Bayesian conflicting Web data credibility algorithm: DataCredibility. The experiment results show that the proposed DataCredibility algorithm achieves better accuracy, recall rate and F1 measure value compared with the baseline algorithms.

conflicting Web data; Bayesian theory; credibility; data fusion; DataCredibility

2015-10-11.

国家自然科学基金资助项目(51475097,61473194)；国家社科基金资助项目(14GSD95)；全国统计科研重点资助项目(2013LZ44)；陇原创新人才扶持计划资助项目(14GSD95)；甘肃省财政厅高校基本科研业务费资助项目(GZ14007, GZ14023).

王继奎(1978—),男,副教授,从事数据治理、数据集成、软件过程技术与方法研究. ORCID： 0000-0001-5926-7007. E-mail: wjkweb@163.com

10.3785/j.issn.1008-973X.2016.12.019

TP 311

A

1008-973X(2016)12-2380-06