考虑质量损失的退化系统维护建模
2016-12-16周炳海刘子龙
周炳海, 刘子龙
(同济大学 机械与能源工程学院,上海 201804)
考虑质量损失的退化系统维护建模
周炳海, 刘子龙
(同济大学 机械与能源工程学院,上海 201804)
为有效解决退化系统的预防性维护问题,以“两设备带缓冲区”的系统模型为研究对象,综合考虑产品质量损失和缓冲区的影响,建立以最小化单位运行成本为目标的预防性维护模型.基于田口质量损失理论,构建系统状态与质量损失间的函数关系;针对退化系统中的瓶颈设备和非瓶颈设备,分别建立基于可靠度和时间的预防性维护策略.根据约束理论,以瓶颈设备的预防性维护作为机会维护(OM)的决策点,利用期望成本节余函数来判断是否对非瓶颈设备进行机会维护.利用迭代算法寻找最优决策组合,并通过蒙特卡罗仿真对算例进行分析.结果表明,所建模型是可行且有效的;与计划维护策略相比,机会维护(OM)策略在降低成本和提高产出方面的表现更优.
退化系统;质量损失;缓冲区容量;机会维护;预防性维护;蒙特卡洛法
合理的预防性维护策略可以有效地保障系统的可靠性、提高产出并降低运行成本.缓冲区的设置能够有效地减少因上游设备故障或计划维护而导致的生产系统停滞,因此,带有缓冲区的生产系统的预防性维护问题一直受到学界的关注.Ribeiro等[1]在已知预防性维护策略的条件下,利用整数规划求解了最优缓冲区的大小.Dimitrakos等[2]在已知缓冲区容量的条件下,应用半马尔可夫链(Semi-Markov)求解了上游设备的最优维护状态点.Meller等[3]提出了以缓冲区容量来触发上游设备预防性维护的策略.成国庆等[4]在假设上游设备“修复如旧”的条件下,以最小化系统运行成本为目标,运用几何过程建立了退化系统维修更换模型.Zequeira等[5]以在上游设备停机时最大化满足下游设备所需为目标,研究了缓冲区大小和预防性维护周期的优化.Karamatsoukis等[6]在文献[2]的基础上利用离散时间马尔科夫决策模型研究了带缓冲区的串联设备预防性维护问题.余佳迪等[7]同时考虑上、下游设备的随机退化,提出了基于周期的预防性维护策略.Zhou等[8]针对带有缓冲区的串行系统提出了基于动态规划的机会维护策略.Li等[9]研究了多机串行系统的机会维护和调度联合优化问题.Javid等[10]研究了机会维护在基于状态的预防性维护下的作用效果.Sun等[11]考虑了刀具退化对质量的影响,以系统成本最小化为目标,建立了多设备系统的预防性维护模型.Radhoui等[12]对“非完美”生产系统提出了质量控制与预防性维护的联合优化策略.Lesage等[13]对质量控制在提高维护水平中的潜在作用提出了评价方法.Panagiotidou等[14]提出了利用休哈特图(Shewhart chart)来安排预防性维护的模型.Radhoui等[15]综合考虑质量损失和预防性维护对退化系统成本的影响,提出了基于不合格品数的预防性维护触发机制.上述预防性维护模型通常未区分设备种类而采用单一的预防性维护策略,将产品的质量损失和缓冲区的容量同时纳入考虑的研究则鲜有报道.
本文在前期研究[16]的基础上,以约束理论(theory of constraints, TOC)为基础,综合考虑产品的质理损失和缓冲区的容量,针对退化系统中不同设备的“角色”,确定不同的预防性维护策略,以实现在给定任务期内单位运行成本的最小化.在此基础上,以瓶颈设备的预防性维护作为机会维护的决策点,建立非瓶颈设备的动态机会维护模型,实现成本的进一步降低.
1 问题描述
根据TOC可知,瓶颈设备决定了系统的产出,因此可以将系统作如下假设:瓶颈设备的上游机器为非能力约束资源(non-capacity constraint resources, NCCR),视为供应机M1;瓶颈设备及其后面的机器为能力约束资源(capacity constraint resources, CCR),视为瓶颈机M2.退化系统包括供应机和瓶颈机以及两者之间的缓冲区,如图1所示.当缓冲区未满时,供应机以速率p将原材料加工为半成品,存入缓冲区,待其满后,速率保持与瓶颈机的速率一致;瓶颈机以速率d从缓冲区中取走半成品加工成成品.
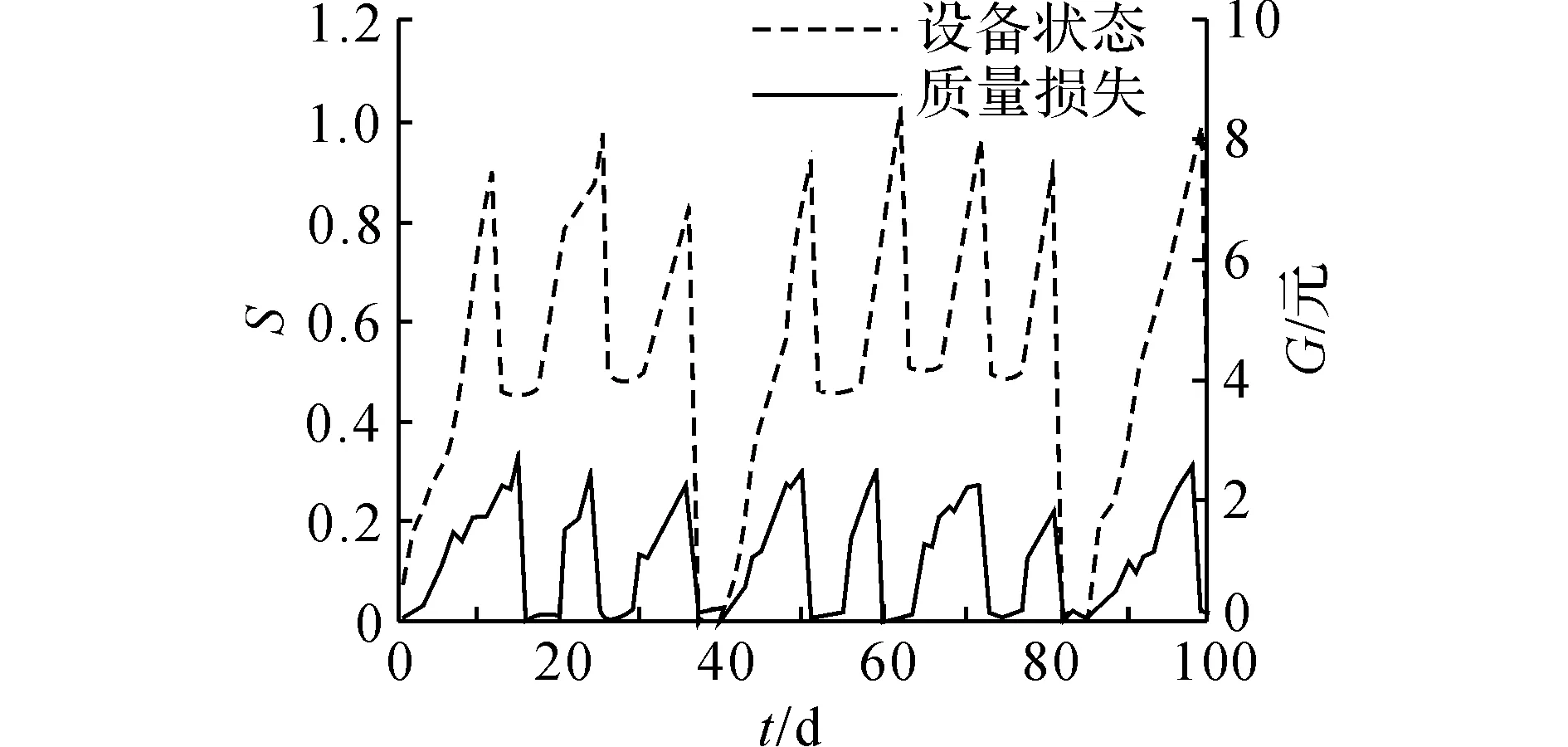
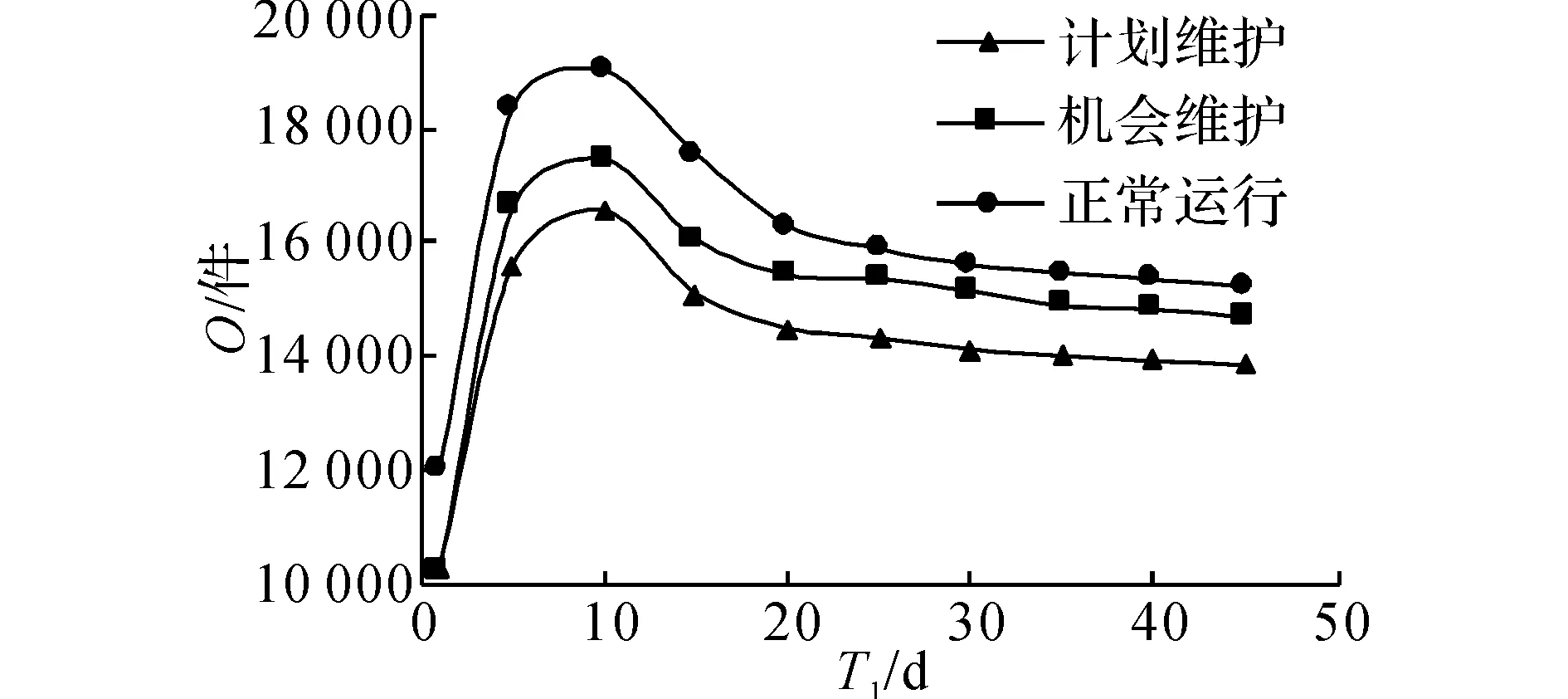
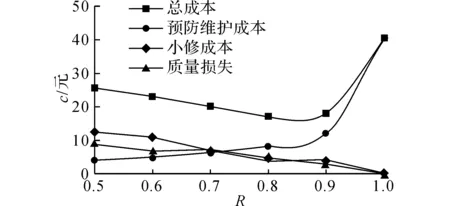
为了更好地描述本文提出的维护建模方法,结合生产实际,作出如下假设.1)缓冲区的最大容量为Bmax,单位产品的库存成本率为ch,缺货成本率为cs.2)两台设备的状态都随使用时间而退化,因此在每个时期末需要对产品质量和设备状态进行检测,以确定本阶段产品质量以及下一时间段内的生产和维护决策,检测可以即时完成.3)系统的初始状态为全新,各设备的故障率hn(t)服从威布尔分布W[βn,ηn],当设备状态达到或超过临界点时则设备发生故障,故障发生后立即采用“小修”模式维修,且“修复如旧”,小修成本率为cn,cm,其中n=1,2(1为供应机,2为瓶颈机).4)由于M1是NCCR,为了方便维护,采用固定周期的预防性维护和机会维护;M2是CCR,为保证其可靠性,采用基于设备可靠度的预防性维护策略;维护成本率为cn,pm,且cn,pm 图1 带缓冲区的双机系统模型Fig.1 Model of two machines system with buffer 2.1 质量损失 实际生产中,设备状态的退化(如:刀具磨损等)会造成加工品的规格参数波动,并且随着设备退化,这种波动会更大,且这种波动会造成产品质量损失.根据田口质量损失公式[17],质量损失函数可表述为 G(m)=K(m-m0)2. (1) 式中:K为不依赖m的质量损失函数系数,m为产品质量的实测值,m0为产品质量的目标值. 为了描述产品质量特性与设备状态间的关系,在文献[11]的基础上,结合本文设备状态的描述形式,构造两者间的关系函数如下: mj(τ)=α[1-exp (-S(τ)]+m0+δ. (2) 式中:mj(τ)为τ阶段第j个产品的质量;α为影响系数;S(τ)表示τ时设备状态;δ是未纳入模型的噪音,且δ~N(0,σ2).若设备在某一时间段[τi,τi+1]内的产量为Q(τi),则可求该时间段内的质量损失为 (3) 2.2 瓶颈机维护建模 根据假设3)和4),当M2的可靠度达到预定阈值Rpm时需要对其进行维护.可靠性方程为 (4) 式中:t为时间,T2,l为M2的第l个维护周期.在τ时刻,设备的可靠度函数为 在实际生产中,一方面设备随役龄的增加故障 率会逐渐提高,另一方面预防性维护通常都“修复非 新”.为了综合这两方面的考虑,引入役龄递减因子 a和故障率递增因子b,则瓶颈设备的故障率公式 h2(l)可表示为 根据假设2),在每个时期末的检测会根据设备 的状态作出下一时期的生产与维护决策,变量的表 示如下: (7) (8) 式中:X(τ)表示时刻τ的生产决策,U(τ)表示时刻τ的维护决策.由此,在任意时刻τI,瓶颈机的状态可以描述为 (1-X2(τi))[ΔsU2(τi)+(1-U2(τi))S2(τk)]}. (9) 式中:Δs是单位时间段内的退化量. 由假设4),当R(τI)≤Rpm时,需要进行预防性维护.若当前τI为维护起始时时刻,维护时长为tpm,则满足 (10) (11) 其中,式(10)为生产约束,表示维护阶段不进行生产;式(11)为维护约束,表示该阶段为预防性维护. 当R(τI)>Rpm且当前状态S2(τI)大于失效阈值S2,bd时,进行“小修”,即故障维修(correctivemaintenance,CM),维护时长为tcm,并满足 (12) (13) 其中,式(12)为生产约束,表示“小修阶段”不进行生产;式(13)为维修约束,表示该阶段为小修. 由以上策略可知预防性维护的间隔期不一定相等,因此,模型以整个加工周期内的单位运行成本最小化为目标.所考虑的成本因素有质量损失、维护成本和惩戒成本,计算方法如下. (14) (15) 式中:Δτ为[τi,τi+1]的时长,本文取Δτ=1.式(14)为产量约束,保证瓶颈机的产量不会超过期初库存量与本期供应机产量之和.式(15)为产能约束,保证产量不超出瓶颈机的能力.总的质量损失为 (16) (17) 3)惩戒成本:瓶颈机决定了整个系统的产出,而实际产出必然低于理想值,为了尽量缩小差距,施以惩戒成本.假设单位成本为c2,th,则整个任务周期内的惩罚成本为 (18) 此外,当供应机处于维护状态且缓冲区内的在制品消耗殆尽时,会导致瓶颈停产,发生缺货.缺货成本在本节不予考虑,将在缓冲区建模中予以体现. 2.3 供应机维护建模 2.3.1 固定周期的计划维护 对于供应机,采用固定周期的预防性维护策略.假设维护周期为T1,pm,整个任务周期可划分为N次.假设前一次维护结束时刻为τk. (19) 式(19)约束了预防性维护阶段不进行生产. (20) 式(20)约束了“小修”阶段不进行生产. 基于以上维护策略,供应机在任务期内发生的成本如下. 1)质量损失:每个时期τ内的产量为 (21) (22) (23) 3)惩戒成本:当缓冲区已满且瓶颈机处于维护时,供应机将发生闲置,造成能力上的浪费.若单位能力惩罚成本为c1,d,则总的能力惩罚为 (24) E(ccm)=c1,cmΔtcm= (25) 式中:“new”为新周期,“old”为原周期,Δtcm为小修的期望总时长. 期望节省的质量损失为 (26) 期望节省的供应机闲置损失与瓶颈机饥饿成本的总和为 (27) 式中:第一个大括号内的式子表示进行机会维护的成本,第二个大括号内的式子表示按原计划维护的成本. 此外,由于供应机提前维护,造成了设备剩余可用能力的浪费,设单位惩罚成本为cw,则总的能力浪费为 (28) 由式(25)~(28)可得,在τb时刻若进行机会维护的期望成本节余函数为 (29) 2.4 缓冲区建模 假设单位产品库存成本率为ch,缺货成本为cs,则在[τi,τi+1]内的缓冲区容量可表示为 B(τi)=B(τi-1)+p(1-|X1(τi)-1|)Δτ- dΔτ(1-|X2(τi)-1|) , (30) B(τi)≤Bmax. (31) 在此,引入二进制辅助变量δ(τ),用1表示发生库存成本,0表示发生缺货成本,即 (32) 则[τi,τi+1]以及整个任务期内的缓冲区成本可分别表示为 cb(τi)= 0.5chδ(τi)|B(τi)-B(τi-1)|+ cs(1-δ(τi))|B(τi)| , (33) (34) G2(Tlen)+C2,m+C2,th+Cb]. (35) 约束:式(1)~(34)并且0 图2 设备状态与质量损失间的关系Fig.2 Relationship of machine state and quality loss 如图2所示为质量特性与设备状态间的函数关系,结果如图2所示.图中,S为状态值,G为质量损失.由图2可知,质量特性随设备状态退化而劣化,表现为质量损失的增加,而当设备状态恢复时,质量特性也随之恢复. 3.1 供应机维护周期T1的分析 图3 各方案(计划维护、机会维护、正常运行)下维护周期对产量的影响Fig.3 Effects of preventive maintenance (PM) period on output under policies of scheduled maintenance, optimistic maintenance and running without maintenance 如图3所示为在确定缓冲区容量和瓶颈机可靠度(Bmax=10,R=0.85)时,在不同的维护策略下,供应机维护周期对系统产出O的影响.图中“正常运行”表示瓶颈机一直正常运行.整体上,系统产量随供应机维护周期的延长先增加后降低,最后在低水平上趋于稳定.分析其原因,瓶颈机在维护过于频繁时得不到足够的输入,导致低产出;而随着维护周期的延长,由于供应机的过多失效导致系统产出降低.这一结果也与前人的分析相一致[4,6],从而验证了所建模型及方法的正确性.由图3可知,当缓冲区容量不能在供应机失效时满足瓶颈机的需求时,对供应机进行动态机会维护可以节省停机时间,从而提高系统产出. 图4 各方案(计划维护、机会维护、正常运行、事后维护)下,维护周期对单位成本的影响Fig.4 Effects of PM period on average cost under polices of scheduled maintenance, opportunistic maintenance, running without maintenance and breakdown maintenance 图5 缓冲区容量对各类成本(总成本、总缺货成本、总库存成本)的影响Fig.5 Effects of buffer size on total cost, total shortage cost and total holding cost 3.2 缓冲区最大容量Bmax分析 缓冲区容量对系统成本的影响主要作用于库存成本和缺货成本.由图5可知,图中c表示单位时间内的成本,随着缓冲区最大容量的提高,库存成本相应提高.最后趋于稳定的原因是周期性预防性维护的实施使得缓冲区尚未达到最大值.缺货成本逐渐降低,最后趋近于0,而总成本也逐渐降低,最后趋于稳定.图6则反映了缓冲区在一定程度上可提高系统产出. 图6 缓冲区容量对系统产出的影响Fig.6 Effect of buffer size on system output 3.3 瓶颈机可靠性R分析 瓶颈机的可靠性直接影响系统的产出,但若为了提高可靠度而过度维护,不仅增加维护成本,也占用生产时间,从而导致产出降低.由图7可知,随着可靠度的提高,PM成本急速增加,CM成本和质量损失相应降低,但总成本先降低后升高.这也说明瓶颈机的可靠度并非越高越好.图例中,单位运行成本最低时为22.63元,对应可靠度为0.83;而图8反映了产出随可靠度的变化曲线,最大产出为23 151件,其对应可靠度为0.90,说明两目标下的最优可靠度可能相异.机会维护的实施使得最大产出提高为23 636件,对应的可靠度为0.89. 图7 瓶颈机可靠度对各类成本(总成本、预防维护成本、小修成本、质量损失)的影响Fig.7 Effects of realiability on total cost, PM cost, CM cost and quality loss 图8 2种方案(计划维护与机会维护)下,瓶颈机可靠度对产出的影响Fig.8 Effects of realiability on output under scheduled maintenance and opportunistic maintenance 3.4 计划维护与机会维护策略的对比 表1 计划维护和机会维护方案下最优解组合对比 Tab.1 Comparison of optimal combinations under scheduled maintenance and opportunistic maintenance 最优解组合 计划维护 机会维护 RBmax/件T1/dC/元O/件C/元O/件0.9843822.972409722.0625.6920.9536720.412483219.6226.2610.9035824.162405423.8725.5160.8539829.242318828.0124.6520.8031833.422210435.1223.148 当[T1,Bmax,R]的值为[7,36,0.95]时,单位运行成本最低值20.41元,产出最高值24 832件;而使用动态机会维护策略,最低成本降为19.62元,系统产出增加为26.261件. (1)产品的质量损失在成本方面占有重要部分,而设备的状态对产品质量具有直接影响. (2)维护周期长短、缓冲区大小以及预防性维护阈值对系统的表现具有综合的影响,需要权衡决策. (3)区分对待瓶颈设备与非瓶颈设备的综合预防性维护模型比传统不做区分的维护更加有效. (4)基于TOC提出的成本节余函数可以用于确定机会维护的实施,且机会维护策略能够很好地降低成本、提高产出. (5)蒙特卡洛仿真可以解决模型中的随机失效问题,进而可利用数值迭代算法对问题求解. 本文在考虑质量损失的条件下研究了退化系统的预防性维护问题,对刀具车床、加工中心等设备的维护具有一定的参考作用.未来可进一步探究质量与维护,以及多产品系统的维护问题. [1] RIBEIRO M A, SILVEIRA J L, QASSIM R Y. Joint optimisation of maintenance and buffer size in a manufacturing system [J]. European Journal of Operational Research, 2007, 176(1): 405-413. [2] DIMITRAKOS T, KYRIAKIDIS E G. A semi-Markov decision algorithm for the maintenance of a production system with buffer capacity and continuous repair times [J]. International Journal of Production Economics, 2008, 111(2): 752-762. [3] MELLER R D, KIM D S. The impact of preventive maintenance on system cost and buffer size [J]. European Journal of Operational Research, 1996, 95(3): 577-591. [4] 成国庆,周炳海,李玲,等.考虑缓冲区库存的退化系统最优维修更换策略[J].计算机集成制造系统,2015,21(6): 1593-1600. CHENG Guo-qing, ZHOU Bing-hai, LI Ling, et al. Optimal maintenance strategy for deteriorating systems with intermediate buffers [J].Computer Integrated Manufacturing Systems, 2015, 21(6): 1593-1600. [5] ZEQUEIRA R I, VALDES J E, BERENGUER C. Optimal buffer inventory and opportunistic preventive maintenance under random production capacity availability [J]. International Journal of Production Economics, 2008, 111(2): 686-696. [6] KARAMATSOUKIS C C, KYRIAKIDIS E G. Optimal maintenance of two stochastically deteriorating machines with an intermediate buffer [J]. European Journal of Operational Research, 2010, 207(1): 297-308. [7] 余佳迪,周炳海.带缓冲的串行生产系统预防性维护策略[J].上海交通大学学报,2014, 48(12): 1694-1699. YU Jia-di, ZHOU Bing-hai. Preventive maintenance policy for series production systems with intermediate buffers [J]. Journal of Shanghai Jiaotong University, 2014, 48(12): 1694-1699. [8] ZHOU X, LU Z, XI L. A dynamic opportunistic preventive maintenance policy for multi-unit series systems with intermediate buffers [J]. International Journal of Industrial and Systems Engineering, 2010, 6(3):276-288. [9] LI M, LI H, LIU Q. Integrated production scheduling and opportunistic preventive maintenance in the flowshop manufacturing system [C]∥ The 2nd International Conference on Information Science and Engineering.Moscow: IEEE, 2010: 294-298. [10] JAVID K, JOS A C, BOKHORST, et al. Condition based maintenance in the context of opportunistic maintenance [J]. International Journal of Production Research, 2012, 50(23): 6918-6929. [11] SUN J, XI L, DU S C, et al. Tool maintenance optimization for multi-station machining systems with economic consideration of quality loss and obsolescence [J].Robotics and Computer-Integrated Manufacturing, 2010, 26(2): 145-155. [12] RADHOUI M, REZG N, CHELBI A. Integrated model of preventive maintenance, quality control and buffer sizing for unreliable and imperfect production systems[J]. International Journal of Production Research, 2009, 47(2): 389-402. [13] LESAGE A, DEHOMBREUX P. Maintenance and quality control: a first methodological approach for maintenance policy optimization [J]. IFAC Proceedings Volumes, 2012, 45(6): 1041-1046. [14] PANAGIOTIDOU S, NENES G. An economically designed, integrated quality and maintenance model using an adaptive Shewhart chart [J]. Reliability Engineering and System Safety, 2009, 94(3): 732-741. [15] RADHOUI M, REZG N, CHELBI A. Joint quality control and preventive maintenance strategy for imperfect production processes [J].Journal of Intelligent Manufacturing, 2010, 21(2): 205-212. [16] 周炳海,余佳迪,邵健一.基于可用度评价的串行生产线缓冲分配方法[J].浙江大学学报:工学版,2015,49(5): 893-900. ZHOU Bing-hai, YU Jia-di, SHAO Jian-yi. Buffer allocation method for series production lines based on availability assessments [J]. Journal of Zhejiang University: Engineering Science, 2015,49(5): 893-900. [17] ZHANG J, LI W, WANG K, et al. Process adjustment with an asymmetric quality loss function [J]. Journal of Manufacturing Systems, 2014, 33(1):159-165. Maintenance modeling for deteriorating system considering quality loss ZHOU Bing-hai,LIU Zi-long (CollegeofMechanicalEngineering,TongjiUniversity,Shanghai201804,China) An optimization decision model was built to minimize operation cost per unit time, thus to efficiently solve the preventive maintenance (PM) problem of deteriorating systems. This model considered the production quality loss and influence of buffer, where “two machines with an intermediate buffer” system model was taken as research object. First, a function relation between system status and quality loss was constructed based on the Taguchi quality loss theory. Next, the condition-based PM policy and time-based PM policy were adopted for the bottleneck machines and non-bottleneck machines, respectively. Then, an opportunistic maintenance (OM) policy was proposed based on the theory of constrains (TOC). According to TOC and using PM of bottleneck machines as decision point of OM, the expected cost saving function was used to determine whether to operate OM for non-bottleneck machines or not. Finally, the iterative algorithm was applied to find the optimal decision combinations; Monte Carlo method was applied to analyze the results. Results show that the proposed model is feasible and effective; OM policy is better for saving cost and improving output compared with scheduled maintenance. deteriorating system; quality loss; buffer size; opportunistic maintenance; preventive maintenance; Monte Carlo method 2015-11-13. 国家自然科学基金资助项目(61273035,71471135). 周炳海(1965—),男,教授,博导.从事离散制造系统维护、调度与仿真研究.ORCID: 0000-0002-6599-9033. E-mail: bhzhou@tongji.edu.cn 10.3785/j.issn.1008-973X.2016.12.004 TP 391 A 1008-973X(2016)12-2270-07

2 问题建模

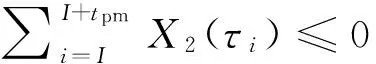
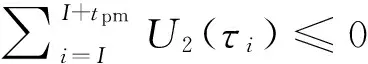

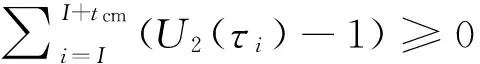
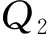






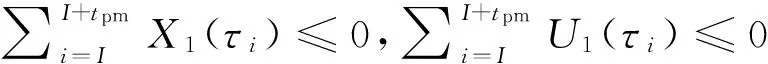

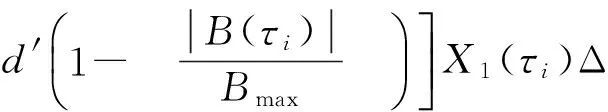

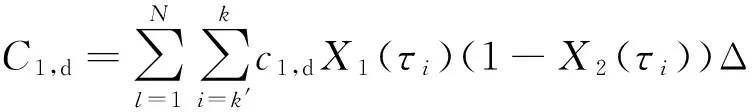
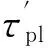

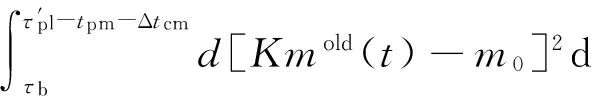

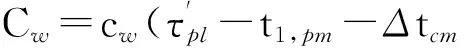
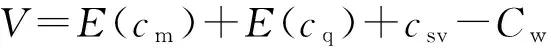
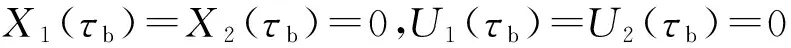

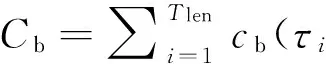
3 数值分析







4 结 论
