乘用车稳定性自抗扰控制策略

刘 刚, 靳立强, 王 熠

(1. 吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130025; 2. 河南工学院 自动控制系, 河南 新乡 453000;3. 燕山大学 信息学院计算机教学实验中心, 河北 秦皇岛 066004)



乘用车稳定性自抗扰控制策略

刘 刚1,2, 靳立强1, 王 熠3

(1. 吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130025; 2. 河南工学院 自动控制系, 河南 新乡 453000;3. 燕山大学 信息学院计算机教学实验中心, 河北 秦皇岛 066004)

为了提高汽车驾驶过程中的安全性能,研究传统乘用车的操纵稳定性控制策略,并采用分层控制结构设计稳定性控制系统.控制策略包含参考模型、UniTire轮胎模型、参数估计模块,控制量期望值计算模块、自抗扰控制(ADRC)部分及直接横摆力矩分配和滑移率控制模块.采用动力学计算的方法估计质心侧偏角,将估算得到的质心侧偏角和传感器采集得到的横摆角速度作为控制变量.当控制变量超过设定门限值时,采用ADRC计算横摆力矩.基于UniTire轮胎模型建立主动横摆力矩和车轮滑移率的关系确定目标滑移率,通过变参数PID实现滑移率控制.应用硬件在环仿真(HILS)平台分别进行单移线和双移线仿真实验,结果表明：所提出的稳定性控制策略能够提高车辆的操稳性能,使得控制变量能够紧密跟踪期望值.

自抗扰控制(ADRC)；车辆动力学；电子稳定控制系统；横摆力矩控制；硬件在环仿真(HILS)

车辆电子稳定系统(electronic stability program, ESP)是汽车主动安全技术领域一个重要的研究方向.ESP用于保证汽车在行驶过程中的稳定性,即在车辆出现转向不足或者转向过多危险情况时,ESP通过发动机转矩与制动转矩产生直接横摆力矩来纠正车辆行驶状态,从而保证车辆的稳定状态.ESP产品目前只有博世、大陆等外企能够生产,国内尚无相关产品.关于ESP系统的大量研究,集中在直接横摆力矩的控制算法和横摆力矩分配策略.目前在接横摆力矩控制算法方面,滑模控制[1]、模糊控制[2]、模型预测控制[3]、H∞算法[4]等已有运用.在横摆力矩分配策略方面,Yang[5]采用二次规划法设计横摆力矩分配器,采用有效集法求车轮横摆力矩分配最优解.付皓[6]利用转矩矢量进行力矩分配,实车试验表明,这类方法有效提高了电动车的侧向稳定性能.Li等[7]提出了基于车载轮胎模型的横摆力矩分配和制动压力控制方案,并讨论了轮胎模型不准确和极限附着椭圆偏差2种情况下的目标值选取方法.Chen等[8-10]将横摆力矩分配和目标滑移率值的确定问题转换成了有约束的优化问题,使用数学方法获得横摆力矩分配最优解.

本文采用分层控制策略,将车辆稳定控制系统分成上、下两层.上层控制器计算车辆稳定所需直接横摆力矩,考虑到车辆在复杂工况下会产生强非线性、模型参数扰动等控制难题,采用自抗扰控制算法来解决车辆行驶过程中的非线性和不确定性的问题.下层控制器用于横摆力矩分配,通过研究UniTire轮胎模型建立直接横摆力矩和轮胎目标滑移率之间的关系,采用自适应变参数比例积分微分(proportion integration differentiation, PID)算法实现滑移率控制.

1 UniTire轮胎模型

车辆动力学性能严重依赖轮胎与路面之间的作用力,因此建立高精度的轮胎模型是车辆电子稳定研究领域的关键问题,本文采用Guo等[11]提出的UniTire轮胎模型计算车辆在复杂工况下轮胎受力.

在UniTire模型中,定义纵向滑移率Sx和侧向滑移率Sy分别为

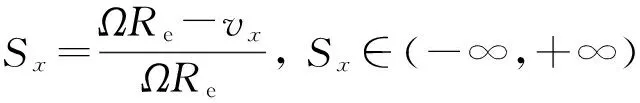
(1)

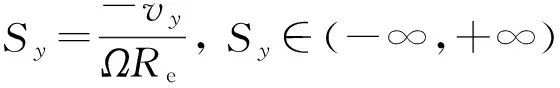
(2)

式中：Ω为车轮角速度,Re为车轮有效半径,vx和vy分别为轮心的纵向速度和侧向速度.

在UniTire轮胎模型中,无量纲的纵向滑移率φx和无量纲侧向滑移率φy分别为

(3)

式中：Kx为纵滑刚度,Ky为侧偏刚度,Fxm和Fym分别为轮胎的纵向力极值和侧向力极值,φ为无量纲总滑移率.

由式(1)～(3)可得UniTire轮胎的侧向力和纵向力分别为

(4)

(5)

式中：Fz为轮胎z轴方向受力；μx为纵向滑移摩擦系数；μy侧向滑移摩擦系数；E为曲率因子,用来调节受力曲线的弯曲度.

考虑到车辆稳定性控制时的加速、制动工况对车轮垂直载荷的影响,车轮载荷为

(6)

式中：Lf和Lr分别为车辆前后轴到车辆质心的距离,hcg为质心到地面的距离,L为前、后轴之间的距离,Bf为车辆宽度.

2 ESP分层控制策略

ESP在汽车实际运动状态偏离驾驶员期望运动状态时主动介入进行稳定性控制.本文设计的电子稳定系统采用分层控制策略,上层控制器负责采用自抗扰控制算法计算稳定性控制所需的直接横摆力矩,下层控制器负责将计算所得横摆力矩分配到被控车轮进行滑移率控制从而实现车辆的稳定性控制.上层控制器的控制变量选择质心侧偏角和横摆角速度,因为质心侧偏角和横摆角速度能够反映车辆的转向特性,其中横摆角速度用来判断车辆转向过程中是否出现转向不足或转向过多的情况,质心侧偏角用来判断在转向过程中是否出现轨迹偏离的情况,两者共同决定了车辆的稳定状况.将这2个变量与其期望值分别作差,当其中任何一个的差值大于介入门限值时,就采用自抗扰算法进行横摆力矩计算.下层控制器首先根据车辆状态判断选取被控车轮,然后根据上层计算所得横摆力矩和UniTire轮胎模型计算得出目标滑移率,通过采用自适应变参数PID算法实现滑移率控制,从而使得车辆状态达到稳定.如图1所示为控制策略架构图.

图1 车辆电子稳定性控制策略架构图Fig.1 Architecture of proposed vehicle electronical stability controlscheme

3 上层控制器设计

3.1 理想横摆角速度和理想质心侧偏角计算

采用车辆线性二自由度模型稳态响应模型计算横摆角速度和质心侧偏角的期望值.

通过文献[12]所提公式计算得到横摆角速度的期望值为

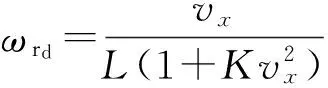
(7)

其中稳定性因数为

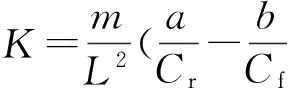
(8)

式中：ωrd为汽车等速圆周运动时的横摆角速度期望值；vx一般采用估算的方法得到,可参考文献[6]；δ为前轮侧偏角,可通过方向盘转角传感器得到；m汽车的质量；Cf为前轮侧偏刚度,Cr为后轮的侧偏刚度.

由于式(7)未考虑路面工况的复杂,因此采用文献[7]中利用附着系数对期望值进行限制,即横摆角速度的期望值的取值范围为

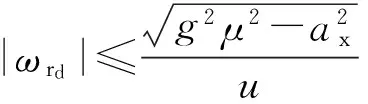
(9)

考虑到模型的瞬态响应特性,增加一阶滞后环节最终得到横摆角速度的期望值为

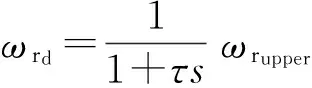
(10)

式中：τ为目标响应时间.

根据二自由度车辆模型做等速圆周运动的情况,在稳态时,可得理想质心侧偏角为

(11)

式(11)是根据侧向力与轮胎的侧偏角成正比而得出的,并未考虑在轮胎附着接近极限值,此时侧向力和轮胎侧偏角已不成线性的关系.根据文献[13-15]中提及的经验结论,即在路面附着系数为0.90时,质心侧偏角的期望值上线为10°；在路面附着系数为0.35的工况下,质心侧偏角期望值上限值为4°,因此修正的质心侧偏角的期望值为

(12)

式中：βupper为质心侧偏角的上限值：

|βupper|=arctan (0.02μg).

(13)

3.2 质心侧偏角估算

质心侧偏角在车辆稳定性控制中多采用参数估计的方法.目前常见的质心侧偏角估算研究多采用卡尔曼滤波、非线性状态观测器等方法.此类方法多是以非线性模型为基础,算法复杂,实时性较差,在实际ESP系统中受限.本文利用线性模型进行质心侧偏角估算.

考虑到在稳定性控制中,车辆的质心侧偏角上限值仅为10°,是一个较小的角度值,将质心侧偏角的公式变化为

(14)

本文设计的电子稳定系统需要每10 ms对质心侧偏角进行一次估算,在10 ms的时间内车辆的纵向车速可以认为是一个常数,因此式(14)的导数为

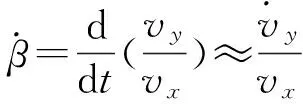
(15)

汽车理论中线性二自由度车辆模型微分方程为

(16)

将式(16)代入式(15)可得质心侧偏角的微分值为

(17)

式中：ay和ωr分别为侧向加速度和横摆角速度,两者均可以通过汽车上的偏航率传感器采样得到.对式(17)求积分即可得到质心侧偏角.

3.3 路面附着系数

采用Fukada[16]提出的利用非线性度的附着补偿系数加侧向加速度的方式确定路面附着系数为

μ=|Gy|+μe.

(18)

式中：μ为路面附着系数；Gy=ay/g,g为重力加速度；μe为附着补偿系数,该系数前轮转角的偏差值之间的关系如图2所示.其中前轮转角偏差为

(19)

式中：vc为特征车速.

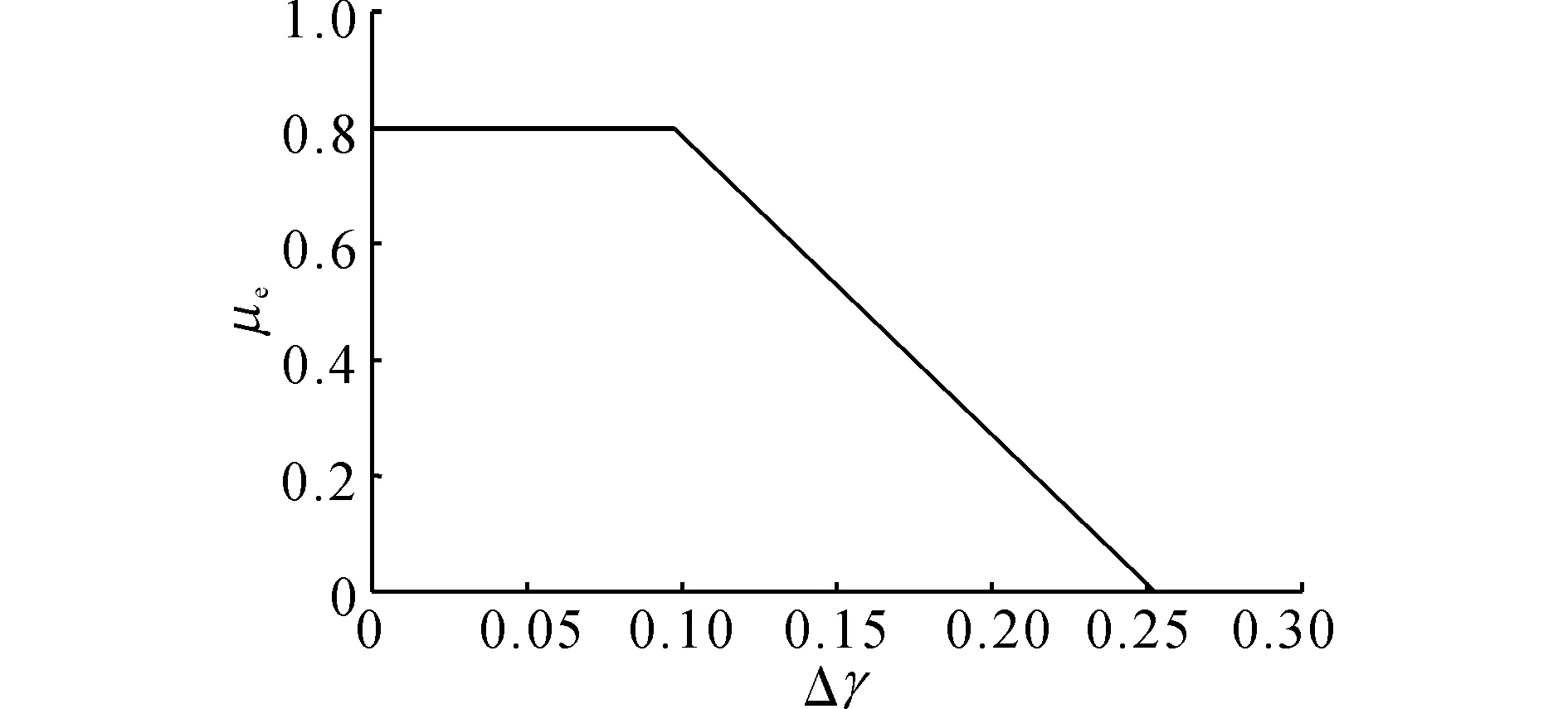
图2 附着补偿系数与前轮转角差值的关系Fig.2 Curve of compensation factor versus front wheel angle difference

3.4 自抗扰控制器设计

自抗扰控制器的模型采用线性二自由度模型:

(20)

(21)

车辆在行驶过程中,利用偏航率传感器采集横摆角速度,然后将其与横摆度速度的期望值相减;当差值大于系统设定的门限值时,基于横摆角速度的自抗扰控制器就会介入控制.基于质心侧偏角的自抗扰控制器同理.

3.3.1 横摆角速度控制

将式(21)改写为以直接横摆力矩ΔM为控制量的仿射模型:

(22)

式中：

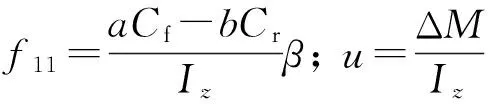
其中，u为输出的直接横摆力矩；f10为模型中的已知部分,其中的变量均可通过传感器测量得到；f11为模型中的未知部分即车辆在运行过程中受到的各种“外扰”和“内扰”的总和作用.

横摆角速度动态方程式(式(22))的扩张观测器为

(23)

式中：

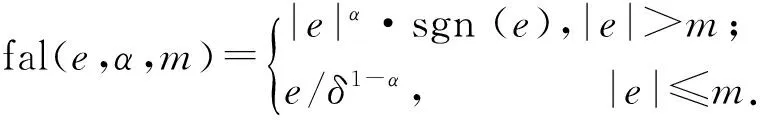
其中，z11为横摆角速度ωr的观测器；z12为式(23)中f11的估计值；α1为滤波因子,取值范围在(0,0.8)；m1为非线性因子；k01和k02皆为输出误差矫正增益；fal(e,α,m)为坐标系下在原点附近的幂次函数.

式(22)的非线性误差反馈控制率为

e2=ωrd-z11,

uωr=k1fhan(e2,α2,m2).

(24)

在自抗扰算法中,k01、k02、k1、α2、m2、b0皆为待调节参数.其中,k01、k02、k1是由系统的采样步长确定的,韩京清[17]提出了与斐波那契数列相关的方法为

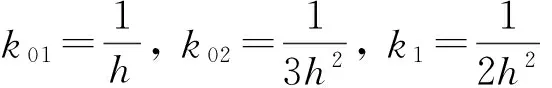
(25)

根据该方法得到观测器系数的范围后,利用Simulink软件最终得到k01=800,k02=30 000,k1=18 000；参数α2为控制量增益,一般取2 000；参数m2和b0分别类似于PID控制算法中的比例增益系数和积分增益系数,利用Simulink软件优化确定m2=600,b0=3.

最终,基于横摆角速度控制的直接横摆力矩为

ΔMωr=Iz(uωr-f10-z12).

(26)

3.3.2 质心侧偏角控制

当车辆运行时质心侧偏角与其期望值的差值达到门限值时,基于质心侧偏角的自抗扰控制器就会介入控制.针对式(18)作如下修改,将其改成以直接横摆力矩ΔM为控制量的一阶仿射模型：

(27)

式中：

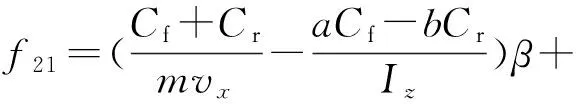
对基于质心侧偏角动态方程式(23)设计扩张状态观测器:

(28)

式中：z21为质心侧偏角β的观测值,z22为f21的估计值.接着对式(26)设计非线性状态误差反馈率为

(29)

式中：k2、k03、k04、α4、m4、b1为待调试参数.由式(25)得到k2=600、k03=28 000、k04=15 000、α4=1 700、m4=500、b1=2.

基于质心侧偏角控制的直接横摆力矩为

ΔMβ=Iz(z22-uβ).

(30)

最终ESP在介入控制时上层控制器输出的直接横摆力矩为

(31)

式中：eβ-lim和erd-lim分别为质心侧偏角和横摆角速度在ESP介入控制时的门限设定值.

4 下层控制器设计

4.1 直接横摆力矩的分配策略

车辆的转向状态可以通过理想横摆角速度和实际横摆角速度的差值进行判断,判断方法如图(3)所示.图中w为横摆角速度偏差的门限值,当偏差值小于门限值时,车辆正处在中性转向状态.而横摆角速度差值大于门限值,且当ωr-ωrd<0时,车辆处于不足转向；相反的情况下则处于转向过度.

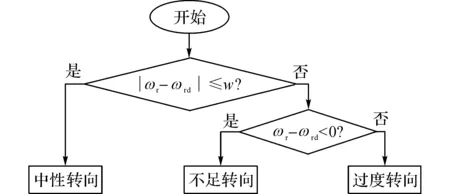
图3 车辆转向状态估算流程图Fig.3 Flow chart of vehicle steering state estimation

直接横摆力矩的分配部分需要考虑2个问题,一个是被控车轮的选择,二则是需要确定被控车轮的目标滑移率.对于目前将直接横摆力矩的分配转换成有约束的优化问题,目前通过优化算法来求出每个车辆的最优解[18].这种将横摆力矩分配到4个车轮的方式可以有效地提高控制效果.但是此类方法算法复杂,实时性不太好,因此本文尽可能地将直接横摆力矩分配到单个车轮,如果分配的纵向力大于轮胎的极限值,则可以选择同侧车轮作为辅助制动轮.当车辆行驶过程中出现转向不足时,ESP介入控制选择内侧后轮作为主要的控制对象;当车辆出现转向过度的情况时,则选择外侧前轮作为主要制动对象,以此减小转向过度的趋势.被控车轮的选择策略如表1所示.

表1 被控车轮选择策略

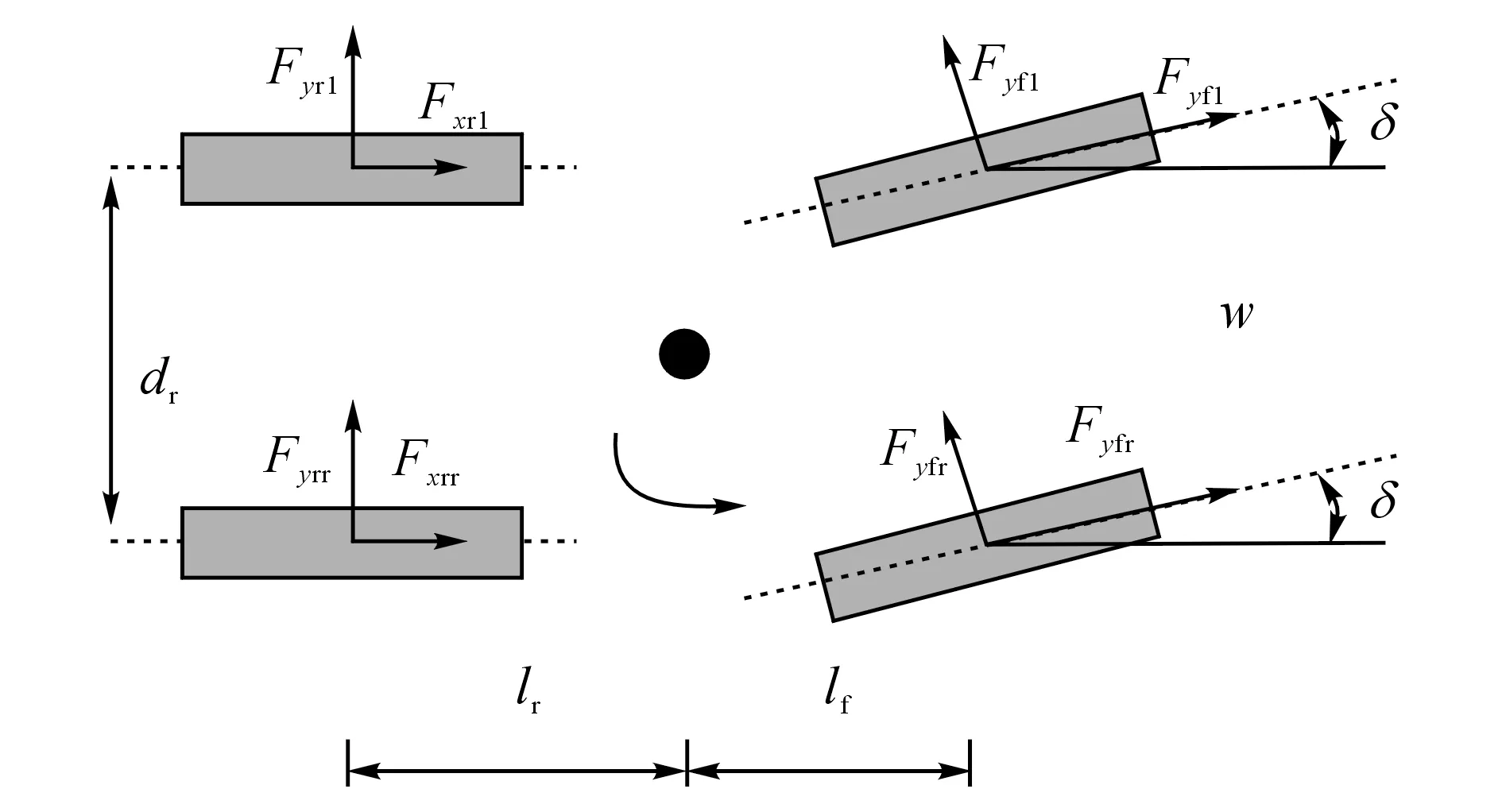
图4 车辆模型中的轮胎受力图Fig.4 Force diagram of tire in vehicle motion model

根据轮胎摩擦圆理论,当汽车的车轮在纵向的滑移率增加Δλ,该轮胎的纵向力则会增加ΔFxfj,同时轮胎的侧向力会减少ΔFyfj.如图(4)所示为车辆模型中轮胎受力图,当ESP介入控制时,前轮有转角,后轮没有转角,因此直接横摆力矩分配至前轮与直接横摆力矩分配至后轮的公式为

(32)

式中：δf为前轮转角,df为车辆宽度,lf为前轴到质心的距离.

由式(32)可知,直接横摆力矩的期望值由轮胎纵向力产生的力矩增量减去侧向力的力矩增量构成,接着我们对该式改写构建横摆力矩的期望值与轮胎滑移率的关系为

(33)

由文献[11]的UniTire轮胎模型得到纵向力公式和侧向力(式(4)),对式(4)纵向滑移率微分后带入得式(33),即可确定直接横摆力矩期望值和轮胎目标滑移率增量之间的关系为

ΔM=g(μ,Fzi)Δλi.

(34)

式中：Δλi为车轮分配得到的直接横摆力矩而引起的滑移率的变化量,μ为地面附着系数,Fzi为车轮的垂直载荷.式(34)中的路面附着系数和车轮垂直载荷可以分别根据式(18)和式(6)计算得出.

4.2 目标滑移率控制

通过将目标滑移率和汽车当前车轮的滑移率做差,即e(k)=λd(k)-λ(k),采用变参数自适应PID计算得到车轮的目标制动压力变化率为

Δp(k)=Kpe(k)+Kie(k)+Kd[e(k)-e(k-1)].

(35)

式中：的比例系数Kp、积分系数Ki及微分系数Kd的值均可根据滑移率差值e(k)进行选取,如表2所示,表2中E1=0.2,E2=0.5,e为滑移率差值e(k)在当前周期的值.

表2 自适应比例积分微分(PID)控制参数值列表

Tab.2 Parameters of adaptive proportion integration derivative (PID)

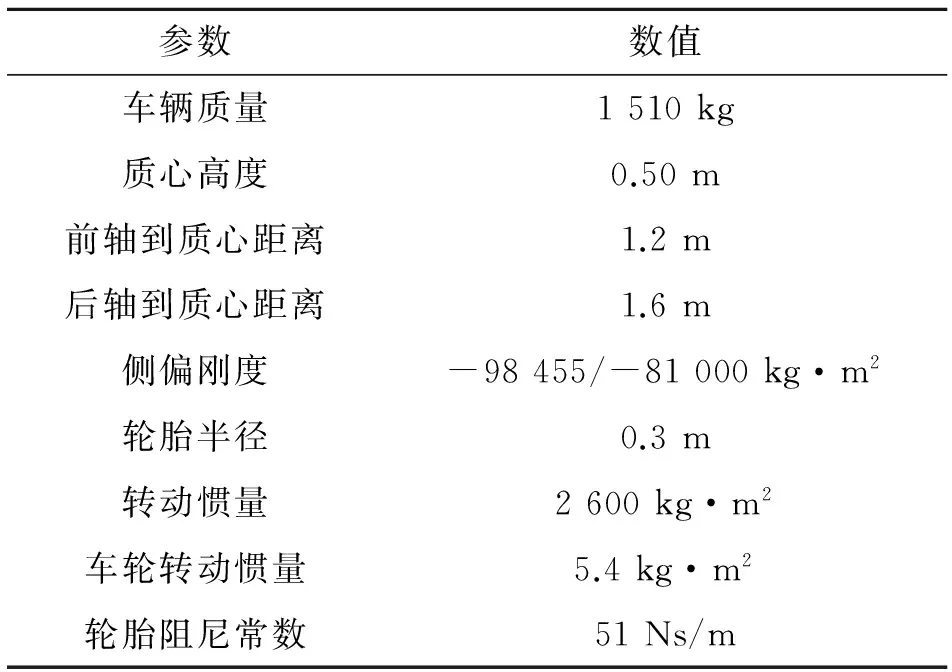
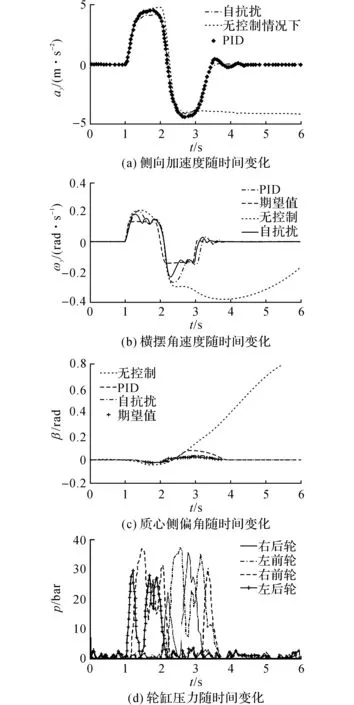
ePIDe>E2300115E1

5 硬件在环仿真

图5 硬件在环仿真HIC平台及车辆电子稳定系统(ESP)控制器Fig.5 Image of Hardware-in-the-loop (HIL) and electronic stability program (ESP) controller circuit

为了验证本文提出的控制策略,采用基于dSpace硬件在环平台(Hardware-in-the-Loop, HIL)进行一系列的实验.硬件在环平台是将部分硬件系统与计算机仿真软件系统结合起来,硬件部分能够准确反映系统的机械特性及液压特性,仿真软件能够模拟各种路况,通过这种方式验证算法的有效性和可靠性.如图5所示为项目组设计的硬件在环仿真平台和ESP控制器.

如图6所示为硬件在环平台的结构原理图.平台采用了dSpace公司的Simulator仿真系统及MicroAutobox快速原型控制器.通过计算机将Carsim整车模型下载并连接到Simulator中,再将本文基于Matlab/simulink的ESP控制策略下载至MicroAutobox.

图6 硬件在环平台结构原理图Fig.6 Architecture of HIL stucture

驾驶员通过方向盘、驱动踏板将方向盘转角信号和踏板位置信号输入Simulator中.同时Simulator根据实时工况,通过CAN总线和IO口将纵向加速度、侧向加速度、横摆角速度、轮速信号输出至ESP控制器.MicroAutobox作为ESP控制器,接收Simulator和驾驶员输入的车辆状态信号和传感器信号.MicroAutobox中的ESP控制策略根据车辆状态及路况进行实时计算,将控制指令以PWM信号的方式发送给液压调节单元,通过液压调节单元中的电磁阀和液压泵驱动制动执行机构,实现车辆的主动安全控制,最后通过轮缸压力传感器将压力信号送至ESP控制器以实现闭环控制.其中ESP控制器部分可以采用MicroAutobox,也可将Simulink的ESP控制算法生成C代码下载至32位的单片机,将单片机作为ESP控制器.

本文在单移线和双移线工况上进行仿真实验以验证稳定性控制策略的效果.仿真车型数据如表3所示.仿真条件设置如下：车速110 km/h,在附着系数为0.35和0.85的工况下只做转向操作,车辆没有加速或者制动的信号输入,进行3种工况的仿真，分别是关闭ESP功能、基于PID算法的ESP控制器和以本文提出的算法作为控制器.

表3 某乘用车技术参数

如图7所示在单移线工况下的仿真结果.图中t表示时间,p表示轮缸压力.如图7(a)所示为侧向加速度实验结果,在关闭ESP功能后车辆在2.5 s时就表现出了失稳状态；采用自抗扰算法控制的车辆的侧向加速度的变化趋势紧密跟随方向盘转角变化趋势；PID算法控制下的车辆的侧向加速度未能及时跟随方向盘转角变化趋势,且在回正的过程中波动较大.如图7(b)和图7(c)所示分别为横摆角速度和质心侧偏角的仿真结果.从图中可以看出,采用本文算法控制的车辆的横摆角速度和质心侧偏角的值紧密跟随期望值,而采用PID算法控制的车辆对目标值的跟随性能较差.如图7(d)所示为本文算法控制下的车辆4个车轮的轮缸压力,本文提出的下层算法通过调整被控车轮的制动压力实现目标滑移率的控制.

图7 单移线工况下硬件在环实验数据Fig.7 Simulation results of HIL during single lane

如图8所示为双移线工况下的实验结果.该工况下的仿真条件设置为时速110 km/h,路面附着系数为0.85的高附着路面,车辆在仿真过程中没有加速、制动的信号输入.如图8(a)所示为双移线工况下的侧向加速度结果,关闭ESP功能的车辆在4 s时出现失稳状态.由图可见,本文提出的自抗扰控制的车辆的侧向加速度跟随方向盘转角变化趋势的性能优于PID算法.如图8(b)和(c)所示为横摆角速度和质心侧偏角的实验数据,本文提出的算法紧密跟随期望值,且将质心侧偏角的值控制在10°以内(根据文献[9],在附着系数为0.9的路面,质心侧偏角的上限值为10°),保证了车辆稳定性,控制效果要优于PID控制.

图8 双移线工况下硬件在环实验数据Fig.8 Simulation results of HIL during double lane

6 结 语

本文针对传统乘用车提出了基于自抗扰控制的ESP控制策略.ESP控制策略采用分层控制的方法,上层进行相关参数的估计及控制量期望值的计算,当质心侧偏角和横摆角速度两者中任一超过门限值后,采用自抗扰控制算法计算直接横摆力矩的计算.下层负责直接横摆力矩的分配,依靠直接横摆力矩和目标滑移率之间的数学关系进行被控车轮的选择,再进行滑移率控制,从而提高直接横摆力矩的控制精度.

基于dSpace硬件在环实验平台的单移线和双移线实验表明：与PID控制算法相比,本文所提控制策略显著增强了汽车在复杂工况下的操稳性能；该方法能够有效准确估计质心侧偏角,且准确地跟踪控制变量的理想值.下一步研究将针对车辆状态参数准确估计,从而最终实现ESP产品化.

[1] 林程,彭春雷,曹万科.独立驱动电动汽车稳定性的滑模变结构控制[J].汽车工程,2015, 37(2): 132-138. LIN Cheng, PENG Chun-lei, CAO Wan-ke. Sliding mode variable structure control for the stability of independent drive electric vehicle [J]. Automotive Engineering, 2015, 37(2): 132-138.

[2] 许建,张政,李翔,等.独立驱动电动汽车横摆力矩的模糊控制算法[J].西安交通大学学报,2014,48(7): 83-91. XU Jian, ZHANG Zheng, LI Xiang, et al. A fuzzy control system for the direct yaw moment of 4WD electric vehicles [J]. Journal of Xi’an JiaoTong University, 2014, 48(7): 83-91.

[3] 邹广才,罗禹贡,李克强.基于全轮纵向力优化分配的4WD车辆直接横摆力矩控制[J].农业机械学报, 2009, 40(5): 1-9. ZHOU Guang-cai, LUO Yu-gong, LI Ke-qiang. 4WD vehicle DYC based on tire longitudinal forces optimization distribution [J].Transactions of The Chinese Society for Agricultural Machinery, 2009, 40(5): 1-9.

[4] 玄圣夷,宋传学,靳立强,等.基于多级鲁棒PID控制的汽车稳定性控制策略[J].吉林大学学报：工学版,2010,40(1): 13-18. XUAN Sheng-yi, SONG Chuan-xue, JIN Li-qiang, et al. Multilevel robust PID control strategy for vehicle stabilitycontrol [J]. Journal of Science Jilin University： Engineering Science, 2010, 40(1): 13-18.

[5] YANG P. Stability control strategy design and experiment of distributed electric drive vehicle [J]. Journal of Mechanical Engineering, 2013, 49(24): 128-136.

[6] 付皓.汽车电子稳定系系统质心侧偏角估计与控制策略[D].吉林:吉林大学,2008: 76. FU Hao. Research on sideslip angle estimation and control algortihm for vehicle electronic stability system [D]. Jilin: Jilin University, 2008: 76.

[7] LI L, JIA G, CHEN J, et al. A novel vehicle dynamics stability control algorithm based on the hierarchical strategy with constrain of nonlinear tyre forces [J]. Vehicle System Dynamics, 2015, 53(8): 1093-1116.

[8] CHEN Y, HEDRICK J K, GUO K A novel direct yaw moment controller for in-wheel motor electric vehicles [J]. Vehicle System Dynamics, 2013, 51(6): 925-942.

[9] GOODARZI A, MOHAMMADI M. Stability enhancement and fuel economy of the 4-wheel-drive hybrid electric vehicles by optimal tyre force distribution [J]. Vehicle System Dynamics, 2013, 52(4): 539-561.

[10] SHUAI Z, ZHANG H, WANG J, et al. Lateral motion control for four-wheel-independent-drive electric vehicles using optimal torque allocation and dynamic message priority scheduling [J]. Control Engineering Practice, 2014, 24(1): 55-66.[11] GUO K, LU D, CHEN S K, et al. The UniTire model: a nonlinear and non-steady-state tyre model for vehicle dynamics simulation [J]. Vehicle System Dynamics, 2005, 43(1): 341-358.

[12] SONG P, TOMIZUKA M, ZONG C. A novel integrated chassis controller for full drive-by-wire vehicles [J]. Vehicle System Dynamics, 2015, 53(2): 215-236.

[13] LI L. Progress on vehicle dynamics stability control system [J]. Journal of Mechanical Engineering, 2013, 49(24): 95-110.

[14] YAN C, WANG J. Energy-efficient control allocation with applications on planar motion control of electric ground vehicles[C] ∥ American Control Conference 2011. San Francisco: [s. n.], 2011: 2719-2724.

[15] HE P, HORI Y, KAMACHI M,et al. Future motion control to be realized by in-wheel motored electri vehicle[C] ∥ 31st Annual Conference of IEEE. Raleigh: [s. n.], 2005: 263-283.

[16] FUKADA Y. Slip-angle estimation for vehicle stability control [J]. Vehicle System Dynamics, 1999, 32(4/5): 375-388.

[17] 韩京清.扩张状态观测器参数与斐波那契数列[J].控制工程,2008,15(2): 1-3. HAN J Q. Parameters of the extended state observer and Fibonacci sequence [J]. Control Engineering of China, 2008,15(2): 1-3.

[18] BUCCHI F, FRENDO F. A new formulation of the understeer coefficient to relate yaw torque and vehicle handing [J]. Vehicle System Dynamics, 2016, 54(6): 1-22.

Vehicle stability control system based on active disturbance-rejection control strategy

LIU Gang1,2, JIN Li-qiang1, WANG Yi3

(1.StateKeyLaboratoryofAutomotiveSimulationandControl,JilinUniversity,Changchun130025,China；2.DepartmentofAutomaticControl,HenanInstituteofTechnology,Xinxiang453000,China；3.YanshanUniversity,QinhuangIsland066004,China)

The steering stability control strategy of traditional passager vehicle was investigated and an electronic stability control system based on hierarchical control strategy was designed to improve safety performance during vehicle driving. The control strategy insisted of reference model, UniTire model, parameter estimation model, desired parameter calculation model, active disturbance rejection control (ADRC) model, direct yaw moment distrubution and slip ratio regulation model. First of all, side slip angle was calculated using dynamics calculation method. Secondly, take the evaluated side slip angle and the yaw rate obtained by sensors as control variables. When the control variables exceeded threshold value, ADRC was adopted to calculate the yaw moment. In order to determine the target slip ratio, the relation between active yaw moment and wheel slip ratio was built up based on the UniTire model; the variable PID parameters were used to control slip ratio. Finally, hardware in loop simulation (HILS) was taken under single line and double line conditions. Results show that the proposed stability controller strategy can improve the vehicle’s controllability and stability, making the control variable track the expectation closely.

active disturbance rejection control (ADRC); vehicle dynamics; electronic stability control system; yaw moment control; hardware in loop simulation (HILS)

2015-12-08.

国家自然科学基金资助项目(50907030)；中国博士后科学基金资助项目(2013M54024B).

刘刚(1981—).男,博士生.从事汽车底盘电子控制技术研究, ORCID: 0000-0001-8849-169X.E-mail: gliu14@mails.jlu.edu.cn 通信联系人：靳立强(1976—),男,教授.ORCID: 0000-0002-0545-3872.E-mail: jinlq@jlu.edu.cn

10.3785/j.issn.1008-973X.2016.12.007

U 461.2

A

1008-973X(2016)12-2289-08