基于等效铁芯电感的磁通门HSPICE分析模型*

崔智军，杨尚林

（1.安康学院电子与信息工程学院，陕西安康725000；2.西北工业大学电子信息学院，西安710129；3.北方民族大学电气信息工程学院，银川750021）

基于等效铁芯电感的磁通门HSPICE分析模型*

崔智军1，2*，杨尚林3

（1.安康学院电子与信息工程学院，陕西安康725000；2.西北工业大学电子信息学院，西安710129；3.北方民族大学电气信息工程学院，银川750021）

提出了一种基于随电流变化的铁芯电感的磁通门HSPICE（High Simulation Program with IC Emphasis）模型，该磁通门模型铁芯的磁滞回线使用反正切函数来描述，其激励与测量线圈等效为一种随电流变化的电感电路模型。本文给出了全电路元件的磁通门模型的参数及提取方法，此模型可以在任意形状的电压激励波形下仿真，与已有的磁通门模型相比，具有仿真精度高、需要参数少且计算容易和可以方便进行输出信号处理的特点。实验和仿真结果对比表明，双铁芯磁通门HSPICE模型仿真的输入电流和输出电压的幅值分别为146 mA和1.03 V，与实际测试的146.6 mA和1.177 V相比，输入电流有0.6 mA的误差，输出电压有0.147 V的误差。

磁通门传感器；HSPICE模型；磁滞回线；非线性电感

磁通门传感器（简称磁通门）是利用软磁铁芯的非线性特性在周期激励磁场下调制外界磁场而检测外磁场方向和大小的磁性传感器［1］。它能测量大小在10-10到10-4T的直流或是低频磁场，且具有nT级的稳定性和0.1 nT的分辨率，是一种具有很好综合性能［2］的弱磁场测量传感器，在工业、军事、航空航天、生活消费等方面都有广泛的应用。

合适的磁通门模型分析方法对于磁通门的性能改进和参数调整具有重要的意义，通常通过数值模型分析磁通门的方法主要有：有限元分析、利用各种模型的SPICE仿真、利用物理关系式和利用数值方法解模型的微分方程的分析方法。Andrea Bas⁃chirotto［3］等应用Flux3D和Magnet 6.0有限元分析软件对磁通门进行了仿真优化；Hector Trujillo等［4］用SPICE（Simulation Program with IC Emphasis）对磁通门进行了建模仿真；刘诗斌［5］、张学孚［6］、JOHN R［7］等都给出了分析磁通门的理论公式，根据公式中的参数对传感器进行优化分析；王锋［8-9］、蒋顺平［10］、何乃明［11］等用解微分方程的方法对电压激励的磁通门进行建模仿真。在这些分析方法中用有限元方法进行分析仿真时间较长且用电压激励有时候难以完成仿真；用SPICE或是用功能相似的软件仿真时，有些对铁芯磁性能仿真的模型过于简单，有些比如Jiles-Atherton（JA）模型［12］或是改进后的JABrachtendorf模型［13］，它们是被大家知晓和应用最广泛的磁通门应用模型，但是对于很多类型的磁性材料，虽然它们很符合物理意义，但都不容易从测量数据中得到模型参数，复杂的数值计算的优化过程是不可避免的。对磁通门建立理论公式进行分析大多数情况下都是电流激励的，这与实际绝大部分是用电压激励的情况不一致。建立微分方程的方法分析磁通门虽然解决了电压激励的问题，但也有其数值计算速度较慢和不能与微型磁通门片上系统的后续电路相关联进行仿真分析的缺点。

本文建立了一种基于等效铁芯电感的磁通门HSPICE模型，用一个随电流变化的电感来模拟铁芯的磁特性，此模型中需要磁滞回线数据较少且参数计算方便，同时很容易的加入到等效电路中来模拟磁通门后续信号处理过程。

1 铁芯模型描述

1.1 等效铁芯电感

铁芯磁特性的描述对于磁通门建模至关重要，正确的描述铁芯的变化，才能正确描述磁通门的性能。铁芯通过线圈与电路进行电磁耦合，它将外界磁场和电路联系起来。软磁材料铁芯通过激励磁场和外界磁场的共同作用，在其内部的磁感应强度也随之变化，此时在其上缠绕的线圈上产生变化的感应电动势。这个过程就是外部电压随电流的变化而变化，这与电感的变化很相似，但是此时的电感是一个随电流变化的电感。根据磁介质磁通链的定义、安培环路定理、导数磁导率和电感的定义可以得到如式（1）。

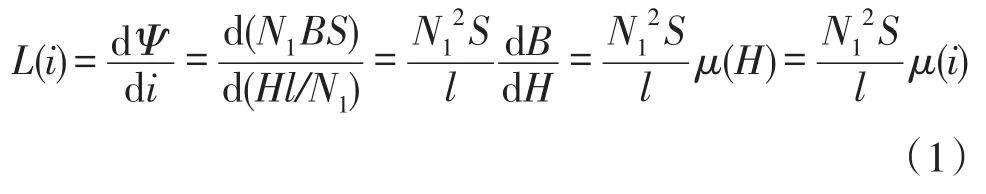
式中，L（i）是等效铁芯电感，Ψ是带铁芯线圈的磁通链，N1是初级线圈匝数，B是带铁芯线圈的磁感应强度，S为铁芯的横截面积，H为铁芯的磁场强度，l是铁芯的有效磁路长度，μ(H)是随磁场强度变化的微分磁导率，μ(i)是随电流变化的微分磁导率。式（1）中N1、S和l可以根据线圈规格和铁芯的几何尺寸获得，通过铁芯的磁滞回线得到 μ(H)，因为实际情况下铁芯在交变磁场下就是按照磁滞回线变化的。μ(i)可以通过安培环路定理换算得来。

1.2 铁芯迟滞回线

磁通门铁芯磁滞回线描述的准确性直接决定了整个磁通门模型的准确性。由于反正切函数（atan）的‘S’形状与磁滞回线形状接近，在数据量较少的情况下，拟合磁通门铁芯特性亦可获得较好的效果，采用如下式（2）分别拟合铁芯磁滞回线的上升和下降曲线数据，其中a、b和c是拟合参数。

1.3 铁芯迟滞回线数据采集与拟合

本文使用NI（National Instruments）公司的数据采集卡（NI PCI-6250）和测试原理如图1所示的自制实验装置测试了实验铁芯坡莫合金1J85的磁滞回线，这样做避免了考虑退磁效应，可以测得要求频率下的磁滞回线。

图1 Labview测试磁滞回线原理图

在Labview测试系统中，激励电压为幅值3 V、频率1 kHz的正弦波，频率1 kHz符合磁通门的应用频率。其中铁芯的有效磁路长l为30 mm，横截面积S为0.1 mm2。对采集到的电阻两端的电压根据安培环路定理进行比例缩放，对于线圈输出电压进行积分和比例缩放，最后利用如图1所示的系统测试铁芯坡莫合金1J85的磁滞回线如图2所示。

图2 Labview测试1J85的磁滞回线

本文利用Matlab拟合工具箱，运用 B=a× arctan(b×H±c)函数分别对如图2所示的磁滞回线的上升和下降曲线数据进行非线性最小二乘拟合，上升阶段式（2）中参数c取负，下降阶段则取正。分别用上升和下降阶段两组拟合参数a、b、c的平均值作为拟合参数，得到a=0.386 1，b=0.008 317，c=0.225 4，拟合后的均方值误差的平均值为0.013。拟合后的图形如图3所示，其中点是原始数据，实线为拟合后的曲线。包含10个参数的JA模型需要大量的实验数据以及很复杂的数值优化过程才能最终确定这10个模型参数，故稳定性差［14-15］；本文使用包含3个参数的反正切函数拟合铁芯磁滞回线，且这3个参数仅通过最小二乘拟合取平均值即可获得，所以本文的拟合方法对初值不敏感、与估计方程次序无关且不会出现不收敛的情况［12］。最后拟合后的磁滞回线的曲线函数式为：

则微分磁导率为：

图3 arctan函数拟合磁滞回线图

2 磁通门分析模型

2.1 双铁芯磁通门原理

双铁芯磁通门是一种比较常见的磁通门传感器，它的构造简单且易于加工。它是由两个单铁芯磁通门组合而成，它们的测量线圈顺接，激励线圈反接。在交变激励信号的任何时间，外磁场都与某个铁芯内的磁场相同，与另外一个铁芯内的磁场相反。双铁芯磁通门的示意图如图4所示。

图4 双铁芯磁通门

2.2 双铁芯磁通门HSPICE电路模型

2.2.1 单铁芯等效模型

单铁芯磁通门是将铁芯插入螺线管组成，在1.1部分已经介绍将铁芯的电磁变化用一个随电流变化的电感表示，铁芯的电磁变化通过螺线管与电路联系起来，这样整个单铁芯磁通门的等效电路就由一个变化的电感串联一个固定线圈电感和一个电阻，再与螺线管线间电容并联构成初级。次级通过铁芯与初级线圈耦合，构成与初级类似。整个单铁芯的等效模型如图5所示。1、2端为线圈初级，3、4端为线圈次级。

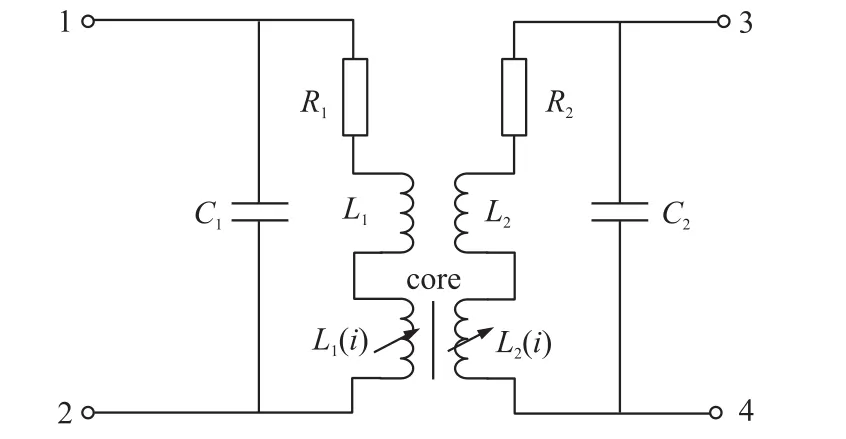
图5 单铁芯等效模型图

2.2.2 双铁芯等效模型

因为磁通门是由两个单铁芯磁通门构成，双铁芯磁通门等效模型是两个单铁芯磁通门的串联，只是这里为了区分螺线管的缠绕方向以符合双铁芯磁通门原理，将两个单铁芯磁通门的初级正向串联，次级反向串联，规定外磁场相对于两个铁芯的方向相反。双铁芯等效模型如图6所示，为了有效区别，将其中一个单铁芯磁通门的标记符号都加了一撇，其中双铁芯等效模型的初级的2端和1′端相连，次级4端和4′端相连，外磁场相对两个铁芯的方向相反。激励电压加在1和2′端，次级输出电压为3和3′端。在次级3和3′端加入电容可以对输出信号进行调谐，同时可以与其他信号处理电路相连。

图6 双铁芯等效模型图

2.3 磁通门模型的HSPICE实现

2.3.1 单铁芯HSPICE模型实现

根据2.2.1部分单铁芯磁通门HSPICE电路模型，在HSPICE仿真软件中利用受控源组合、相应的电阻和电容模型来实现单铁芯磁通门电路模型。首先，根据式（1）、式（4）、线圈匝数、铁芯的几何尺寸以及外磁场的影响，得到L(i)为：

式中，螺线管的初级线圈匝数N1为326，外磁场Hx前的正负号分别在两个单铁芯磁通门取值正好相反，来实现前面的双铁芯模型。第二个正负号是由于磁滞回线的磁滞带来的，它随着铁芯中的磁感应强度的斜率正负而负正。其次，等效电路中的其他参数，比如串联电阻R1、R2、串联线圈电感L1、L2以及螺线管的线间电容C1、C2通过MT4090 LCR METER在1 kHz频率测量和经验公式计算得到R1=6.907 Ω、R2=31.92 Ω、L1=66.57 mH、L2=1.413 mH、C1=0.53 pF、C2=0.61 pF。最后，因为是铁芯耦合，确定耦合因数k约为1，则铁芯互感M（i）为：

式中，N2=1 150为次级线圈的匝数，实验证明这样定义铁芯互感是正确的。同理串联的固定线圈互感M为：

在频率为1 kHz、幅值为1 V的正弦波激励下，对单铁芯磁通门进行实验和仿真，结果如图7所示。

单铁芯磁通门模型仿真的输入电流和输出电压的幅值分别为293 mA和2.95 V，与实际测试的293.4 mA和2.947 V相比，输入电流有0.4 mA的误差，输出电压有0.013 V的误差。

图7 单铁芯仿真VS实验

2.3.2 双铁芯HSPICE模型实现

根据2.2.2部分双铁芯磁通门的HSPICE模型，双铁芯磁通门HSPICE模型实际就是两个完全相同的单铁芯磁通门连接在一起，它们的参数是一样的，只是要注意连接的方式和外磁场对两个单铁芯磁通门的影响的不同。同理，在HSPICE仿真软件中利用受控源组合、相应的电阻和电容模型来实现双铁芯磁通门电路模型。在外磁场为50 A/m的情况下，通过施加频率为1 kHz、幅值为1 V的正弦波激励对双铁芯磁通门进行实验和仿真，结果如图8所示。双铁芯磁通门模型仿真的输入电流和输出电压的幅值分别为146 mA和1.03 V，与实际测试的146.6 mA和1.177 V相比，输入电流有0.6 mA的误差，输出电压有0.147 V的误差。原因是由于实验磁通门传感器两个线圈和铁芯不是完全匹配导致基波信号较大、测试环境磁场的误差以及磁滞回线拐点的误差所致。

图8 双铁芯仿真VS实验

3 结论

本文从电感的定义出发，将磁通门等效为一种基于随电流变化的铁芯电感的HSPICE模型。使用反正切函数来拟合磁通门模型铁芯的磁滞回线，而激励与测量线圈则等效为一种随电流变化的电感电路模型。本文详细描述了双铁芯磁通门模型的参数及提取方法；与现有的磁通门模型相比，此模型可以在任意形状的电压激励波形下仿真，同时对磁通门的输入电流和输出电压的仿真结果不论在波形形状还是幅值上都与实际测试相吻合。

［1］Ripka P，Billingsley S W.Fluxgate：Tuned vs.Untuned Output［J］.IEEE Transactions on Magnetics，1998，34（4）：1303-1305.

［2］Ripka P，Janosek M.Advances in Magnetic Field Sensors［J］.IEEE Sensors Journal，2010，10（6）：1108-1116.

［3］Andrea B，Enrico D，Piero M，et al.From a PCB Fluxgate to an In⁃tegrated Micro Fluxgate Magnetic Sensor［C］//IEEE Instrumenta⁃tion and Measurement Technology Conference.Ottawa，2005：1756-1760.

［4］Hector T，Cruz J，Rivero M，et al.Analysis of the Fluxgate Re⁃sponse Through a Simple Spice Model［J］.Sensors and Actuators，1999，75（1）：1-7.

［5］刘诗斌.微型智能磁航向系统研究［D］.西北工业大学，2001：15-18.

［6］张学孚，陆怡良.磁通门技术［M］.北京：国防工业出版社，1995：6-9.

［7］John R B.The Theoretical Output of a Ring Core Fluxgate Sensor［J］.IEEE Transactions on Magnetics，1972，MAG-8（4）：791-796.

［8］王锋，刘仁浩，张有维.三端式磁通门传感器的数学建模［J］.中北大学学报（自然科学版），2008，29（2）：117-119.

［9］王锋，焦国太，安晓红.三端式磁通门传感器的数学建模及数值分析［J］.探测与控制学报，2008，30（5）：22-25.

［10］蒋顺平，曹大平，刘斯.磁通门磁强计激励电路的分段解析模型［J］.武汉大学学报（理学版），2010，56（5）：605-608.

［11］何乃明，洪泽宏.磁通门探测器的数值分析与仿真［J］.海军工程大学学报，2000（5）：34-38.

［12］Liorzou F，Phelps B，Atherton D L.Macroscopic Models of Magne⁃tization［J］.IEEE Transactions on Magnetics，2000，36（2）：418-428.

［13］Brachtendorf H G，Eck C，Laur R.Macromodeling of Hysteresis Phenomena with SPICE［J］.IEEE Transactions on Circuits and Systems II：Analog and Digital Signal Processing，1997，44（5）：378-388.

［14］侯晓伟，刘诗斌，李菊萍，等.磁通门的数值分析与HSPICE仿真［J］.传感技术学报，2013，26（6）：810-814.

［15］侯晓伟，刘诗斌，李菊萍，等.基于HSPICE温度对长条形磁通门输出的影响［J］.传感技术学学报，2012，25（7）：941-944.

崔智军（1978-），男，陕西渭南人，讲师，西北工业大学电子信息学院在读博士生，专业方向为微电子器件与微传感器，现在主要从事微型磁通门传感器研究，Cuizj_163@163.com；

杨尚林（1983-），男，宁夏灵武人，讲师，博士，现在主要从事微型磁通门传感器研究，ysl029@163.com。

HSPICE Analysis Model of Fluxgate Based on Equivalent Core Inductance*

CUI Zhijun1，2*，YANG Shanglin3
（1.College of Electronics and Information Engineering，An kang University，Ankang Shaanxi 725000，China；2.College of Electronics and Information Northwestern Polytechnical University，Xi’an 710129，China；3.College of Electrical and Information Engineering Beifang University of Nationalities，Yinchuan 750021，China）

An HSPICE（High Simulation Program with IC Emphasis）model of the fluxgate based on core inductance with the change of current is proposed.The hysteresis loop of fluxgate core was described with the arctangent func⁃tion for the proposed fluxgate model，the excitation and measurement coils of the fluxgate were equivalent to a cir⁃cuit model that contains a kind of non-linear time-varying inductance.The parameters and the extraction method of the whole circuit element of the fluxgate model were provided.The model can be simulated under arbitrary wave⁃form of the voltage excitation.The proposed model owns the characteristics of high simulation precision，few parame⁃ters，easily calculated parameters and conveniently carried out output signal compared with the previous model.The simulated results showed that the amplitude of input current and output voltage of dual core fluxgate HSPICE simu⁃lation model are 146 mA and 1.03 V，respectively.The input current and the output voltage have errors of 0.6 mA and 0.147 V respectively compared with test results of 146.6 mA and 1.177 V.

fluxgate sensor；HSPICE model；hysteresis loop；nonlinear inductance

TP212.1；TM936.2

A

1004-1699（2016）11-1673-05

EEACC：7230 10.3969/j.issn.1004-1699.2016.11.008

项目来源：国家自然科学基金项目（61461025，61202314）；高等学校博士学科点专项科研基金项目（20126102110031）

2016-04-28 修改日期：2016-07-11