群混合智能算法优化异构WSN的生命周期*

唐玲艳，吴 雪，吴 喆，罗小娟

（华东理工大学信息科学与工程学院电子与通信工程系，上海200237）

群混合智能算法优化异构WSN的生命周期*

唐玲艳，吴 雪*，吴 喆，罗小娟

（华东理工大学信息科学与工程学院电子与通信工程系，上海200237）

为了优化异构无线传感器网络的生命周期，找到尽可能多的连通覆盖子集（CCS），本文建立了以网络覆盖约束、收集约束、连通约束作为目标评价函数的模型。针对该模型，在蚁群算法基础上，引进鱼群拥挤度的概念，解决了蚁群在算法初期陷入局部收敛的问题。实验结果表明，该改进算法比一般蚁群算法具有更好的全局搜索能力和收敛速度，同时针对蚁群算法在构建子集中存在大量冗余节点的问题，提出了关键域法（KFM）判断各子集中冗余节点且利用冗余节点构建新的子集，这不仅能有效提高节点的利用率，而且延长了异构网络的生命周期。

异构无线传感器网络；网络生命周期；连通覆盖子集；蚁群算法；鱼群拥挤度；关键域法

由于大多数传感器设备是由不可再生的电池供电，而评估无线传感器网络的基本准则是网络生命周期［1］，所以如何优化延长网络生命周期的研究成为了无线传感器网络的研究热点和难点。尽管在同构无线传感器网络［2］中存在一些方法来解决这一问题，但是在异构无线传感器网络［3，4］中关于这一问题的研究进展缓慢。本文所考虑的异构无线传感器网络是Sensor和Sink节点半径、数量的异构。针对这种异构，现有延长异构网络生命周期的方法，是找到多组连通覆盖子集［5，6］（每个子集设备可以解决网络覆盖和连通性问题），其中一个子集设备工作，其余设备可以改用节能的睡眠状态。

为了找到尽量多的连通覆盖子集，文献［7］提出了启发式算法，所得到的连通覆盖子集在某些标准下是最优的，但是并不能一定保证网络生命周期的优化。文献［8］提出了基于前向编码的混合遗传算法，该算法没有考虑网络的连通性问题。文献［9］提出了贪婪算法，虽然解决了网络覆盖和连通问题，但该算法只能处理离散点的覆盖问题。文献［10］提出了基于蚁群优化算法最大化异构无线传感器网络的生命周期，它可以处理点覆盖和区域覆盖，但算法初期由于信息素影响，易陷入局部收敛，影响全局搜索能力和收敛速度，同时节点存在大量冗余。针对以上各算法存在的收敛速度慢和节点冗余等问题，本文在蚁群算法的基础上，将鱼群拥挤度的概念引入到蚁群算法中，同时针对子集中的冗余节点，本文提出了用关键域法去冗余的方法。仿真实验表明，该算法具有更好的全局搜索能力和收敛速度，同时提高了节点利用率并且延长异构网络的生命周期。

1 连通覆盖问题描述

在无线传感器网络中，连通与覆盖是两个最基本的问题。覆盖是指利用网络中的传感器节点对整个目标区域进行监测，从而达到信息采集的目的。连通是指网络中任意两个节点之间都能够进行通信，并且连通也是节点自组织形成网络的前提。本文涉及到的连通覆盖问题，不仅需要考虑网络的感知覆盖而且需要考虑网络的连通性需求。

本文构建的异构无线传感器网络通过传感器（Sensor）和收集器（Sink）的配合来解决连通覆盖问题。传感器监测目标并传输监测结果给收集器。收集器转播监测结果到目的地。因此在解决连通覆盖问题的过程中，需要满足以下三个约束条件：（1）传感器对目标区域形成完全覆盖；（2）所有传感器的监测结果都能被收集器所收集；（3）收集器组成一个无线连通网络。如图1所示，圆点代表Sensor，三角形代表Sink，图1所描述的是一层连通覆盖子集需要满足的三个约束条件，可以看出满足了这三个条件，就可以解决感知覆盖和网络连通性问题。

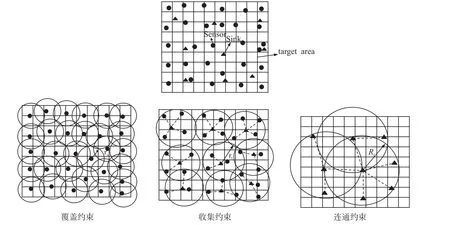
图1 一层连通覆盖子集示意图

2 核心问题描述

2.1 关键区域集CF与优化连通覆盖子集上界值|CF|

在无线传感器网络中，解决连通覆盖问题既需满足感知覆盖也要满足连通性需求，而覆盖只需要满足感知覆盖。因此，在部署相同节点数情况下，满足连通覆盖最优子集的数量少于满足感知覆盖最优子集的数量，即连通覆盖最优子集数可以趋近感知覆盖最优子集的数量但不会超过它，因此感知覆盖最优子集的数量可以作为连通覆盖子集的上界［10，11］，这个上界值称为优化连通覆盖子集（OCCS）。找到感知覆盖子集最优数量是一个NP问题，可以用下面的方法求解。

由于本文涉及到的变量较多，在介绍求解问题之前将本文出现的变量定义如表1所示。

假设在L×W区域里（目标区域初始化网格点）部署了足够多的传感器节点SR={SR1，SR2，SR3，…，SRn}和收集器节点SK={SK1，SK2，SK3，…，，SKm}，当所有传感器节点部署完成后，通过分析传感器节点对目标区域网格点覆盖的情况，将目标区域分为若干区域，如图2所示5个传感器节点把整个目标区域分成15个区域，可知C1={SR1}，C2={SR2}，C3={SR1，SR2}，C4={SR4，SR5}，C5={SR1，SR5}，C6={SR2，SR4，SR5}，C7={SR1，SR2，SR5}，C8={SR1，SR3}，C9={SR3}，C10={SR1，SR3，SR5}，C11={SR2，SR5}，C12={SR3，SR5}，C13={SR2，SR4}，C14={SR5}，C15={SR4}，由文献［7］可知，在目标区域内存在一些关键区域集CF，这些关键区域集由最少传感器节点所覆盖。由图2可知C1，C2，C9，C14，C15五个区域都只被一个传感器节点所覆盖，因此关键区域集CF={C1，C2，C9，C14，C15}。文献［7］中定义优化连通覆盖子集上界值为关键区域集的模，即|CF|=5，则可以找出5层连通覆盖子集。以上述5层连通覆盖子集为例，当其中任意一层子集工作时，其他子集均休眠，若工作的子集生命周期耗尽，启用休眠中的一层子集继续工作，从而达到延长异构无线传感器网络生命周期的目的。

表1 本文变量定义描述

图2 区域与关键区域示意图

2.2 目标评价函数

为了找到尽可能多的满足连通覆盖子集数，并且确保找出的子集是当前最优解，本文构建的目标评价函数是由网络覆盖约束、收集约束、连通约束组成，用它来对各子集进行满意程度评价。以下是目标评价函数的具体描述。

定义一组连通覆盖集S={S1，S2，S3，…，S|CF|}，其中Si∈SR∪SK，表示由传感器和收集器组成的一组子集且i=1，2，3，…，|CF|。用以下三个约束标准来评价每组子集满意程度。

覆盖约束：Si的覆盖率可以直接用作覆盖约束的标准。将监测区域初始化为网格，每个网格是否被传感器节点覆盖作为衡量标准。本文覆盖率Fi表示覆盖的网格面积与整个监测区域面积的比例，如式（1）所示：

式中，Aj表示被覆盖的网格面积，A表示监测区域面积，Si表示第i组连通覆盖子集，SRj表示Si中传感器节点。

收集约束：实现对传感器节点监测信息的收集，则要求每一个传感器节点都至少处于一个收集节点的收集半径内，这样所有的监测信息才能被成功地传输到收集节点。本文在Si中的收集约束可以定义为每组子集能被收集节点有效收集的传感器节点数与其总的传感器节点数的比值，即Xi，如式（2）所示：

式中，CollectNum（SRj）表示在子集Si中，能被收集节点有效收集的传感器节点的数量，AllNum（SRj）表示子集Si中总的传感器节点数量。

连通约束：收集节点收集到的监测信息能有效地传递到目的地，需要收集节点组成一个无线连通网络，当且仅当Gi是一个连接图。基于图论的知识，一个图的连通可以通过它的极大连通子图［12］的相对尺寸Li来测量出来。连通约束标准定义公式如式（3）所示，其中Bi表示极大连通子图中收集节点的数量，Si表示第i组连通覆盖子集，AllNum（SKj）表示子集Si中总的收集节点数量：

上述三个标准值都在［0，1］的范围内。值越大表明找出的子集越优。如果Fi=Xi=Li=1，则Si实现了三个约束条件并且构建了一个连通覆盖子集。应用这三个标准来评估所有的S集，目标优化函数可以定义为如式（4）所示：

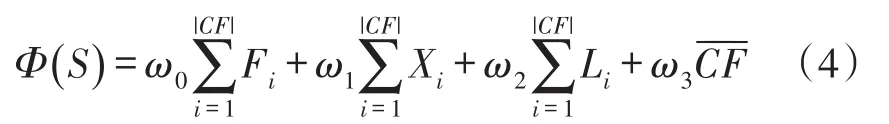
式中，w0，w1，w2，w3＞0是预定义值，是S中连通覆盖子集数量，它随着迭代次数的增加而增加。由式（4）可知，目标函数由两部分组成：第一部分总结了所有子集满足约束条件的情况；第二部分定义了基于连通覆盖数量的目标值。本文提出的算法是通过蚂蚁迭代寻优构建连通覆盖子集，构建过程中可以由式（4）求出该子集的目标评价函数值，并与实验初始设置的目标评价函数值进行比较，将比较值中较大的作为下一次比较的初始值，在每一轮中直到所有蚂蚁完成子集构建，此时目标评价函数值最大的子集即是目前最优子集，重复上述步骤，直到完成最大迭代次数，得到全局优化子集，从而达到寻优目的。

3 群混合智能算法

3.1 蚁群与鱼群混合算法

蚁群算法［13］是Dorigo M等学者于1991年提出的一种优化算法，它以蚂蚁的觅食行为为基础，用蚂蚁的行走路线表示待求解问题的可行解，不依赖于具体问题的数学描述，具有很强的全局优化能力，已广泛应用于解决组合优化问题中的NP完全问题。但蚁群算法本身也存在一些缺点，如收敛速度慢、易陷入局部最优等问题。

鱼群算法［14］于2002年首次提出，通过模拟鱼群的觅食活动来实现空间寻优的一种新智能算法。它具有对初值和参数选择不敏感、简单、易实现、不易陷入局部最优等优势，它主要有觅食、聚群、追尾、随机四种行为。

3.2 群混合智能算法思想

人工鱼群算法和蚁群算法相融合的基本思想：在蚁群算法前期引入鱼群拥挤度，初期可以避免个体过早地集结到信息素高的路径上来，从而可避免算法出现早熟的现象，提高算法的全局寻优能力。在算法后期，由于拥挤度逐渐减为零，完全由蚁群信息素和启发信息来寻优，加速全局收敛。

3.2.1 群混合智能算法构建子集规则

该算法通过鱼群拥挤度、蚁群信息素、启发式信息的共同作用，把节点分配到相应的子集中，然后找到满足连通覆盖的子集，这样在每一轮迭代结束，就可以找出一条当前最优路径。如图3所示，描述是该算法寻优路径的结构构造示意图，图中SRj表示传感器节点，SKj表示收集器节点，灰色线代表蚂蚁的潜在路径，黑色箭头代表蚂蚁选择的一条较优路径。

图3中（v11，v32，v23，v44，v25，v36，v17，v48，v29，v310，v111，v412）（由黑箭头定义），代表一个连通覆盖集S={S1，S2，S3，S4}，其中S1={SR1，SR7，SK3}，S2={SR3，SR5，SK1}，S3= {SR2，SR6，SK2}，S4={SR4，SR8，SK4}是连通覆盖集中的4层子集。根据上述子集构建规则，其步骤描述如下：

Step 1 首先蚂蚁根据路径上的初始信息素浓度和启发式信息的转移概率大小，把当前节点分配到某个子集中。其中使用上述的信息素和启发式信息的设计方法，分配一个未配置的节点j到一个子集Si（i=1，2，…，|CF|）的概率计算如式（5）所示：

式中，Ti（j）表示j节点分配到i子集中的平均信息素浓度；ηi（j）表示j节点被分配到i子集中启发式信息的变化率，如果j节点是传感器节点，则启发式信息表示j节点分配到i子集中覆盖百分比变化量；若j节点是收集器节点则启发式信息是j节点分配到i子集中收集器能有效收集传感器节点的变化率；TK（j）和ηK（j）分别表示j节点分配到任意子集中的平均信息素浓度和启发式信息的变化率；β是一个预定义的参数，用来控制启发信息的影响。

Step 2 按照上述转移概率，把未分配的节点分配到预分配子集时，利用鱼群拥挤度的概念，计算该子集的拥挤度qi（j）如式（6）所示：

如果qi（j）＜σ（t），则表示路径不拥挤，选择当前j节点分配到i子集中，否则，表示该路径拥挤，则在可行邻域内重新计算当前j节点分配到其他子集的期望。其中，σ（t）表示t时刻的拥挤度阈值，按式（7）进行更新：

式中，c为阈值变化系数。

Step 3 重复上述Step1～Step2步骤，直到所有蚂蚁完成子集构建。

图3 构建子集结构示意图

3.3 关键域法（KFM）

在实际应用中，为了保证监控区域被完全覆盖甚至多重覆盖，传感器节点通常大量、随机地部署在监测区域内，从而会产生很多冗余节点。为了除去冗余节点，提高节点利用率，现有的CCP算法［15］、圆周覆盖算法（CCA）［16］在去除冗余节点后网络会产生覆盖盲区，基于Voronoi图［17］的算法计算量大且只能用于同构网络，本文提出了用关键域法去冗余的方法，分别对各子集进行冗余节点判断，不仅不会产生覆盖盲区，而且可以用于异构网络。

如图4所示，传感器节点1，2，3，4，5实现对目标区域完全覆盖。由文献［2］知，图4中灰色区域即为关键区域集（由最少传感器节点所覆盖区域）。要实现对目标区域覆盖，传感器节点1，2，3，4必须存在，剩下节点可能是冗余节点，需要通过进一步计算判断。若移除节点，整个目标区域覆盖率未变化，即为冗余节点，反之不是。由图可知节点5为冗余节点。在判断出所有冗余节点后，对其进行新的子集构建，构建出更多覆盖子集，这不仅提高了节点利用率，同时延长了网络的生命周期。

图4 关键区域判断

3.4 算法流程

本文提出的群混合智能算法是通过鱼群拥挤度、蚁群信息素、启发式信息的共同作用来构建连通覆盖子集，当蚂蚁完成连通覆盖子集的构建后需要进行局部信息素更新，然后利用目标评价函数对各子集进行评优，找出当前最优子集，接着通过关键域法去冗余，构建出更多子集，最后对当前最优子集的节点进行全局信息素更新，直到迭代完成，找出全局优化连通覆盖子集。以下是对算法流程的具体描述：

①初始化节点，设置蚂蚁数m，最大迭代次数max及优化参数（β，τ0，ρ，ζ，w0，w1，w2，w3，c）。

②预估优化连通覆盖子集上界值|CF|。

③基于鱼群拥挤度、蚁群信息素、启发信息构建连通覆盖子集。

④局部蚁群信息素更新：在蚂蚁构建完子集后，对每个子集中任意两个节点J、K间进行信息素更新，并按式（8）更新为：

式中，ρ∈（0，1）是局部信息素更新的蒸发率，τ0表示初始信息素浓度。

⑤评估出当前最优子集Sbs：综合考虑构建的各连通覆盖子集对覆盖约束、收集约束、连通约束的满足程度，通过式（9）目标评价函数进行评估：

⑥对当前最优子集Sbs进行关键域法去冗余。

Step 1 对Sbs各层子集分别进行关键域计算，并判断覆盖关键域的节点，即判断非冗余节点。

Step 2 遍历子集中剩余节点，进行冗余判断。判断标准为：移除节点是否降低目标区域覆盖率，若减少，非冗余节点；反之为冗余节点。

Step 3 对所有冗余节点进行新的子集构建。

⑦全局蚁群信息素更新：为了保留连通覆盖子集的结构特征，吸引更多蚂蚁至全局最优解的周围进行搜索。将去冗余后的优化子集的任意两个节点J、K间进行全局信息素更新，如式（10）所示：

式中，ζ∈（0，1）是全局信息素更新的蒸发率，δτ是信息素浓度增量，由式（11）定义：

⑧算法每一次完成全局信息素更新即算法完成一次迭代，此时如满足停止条件，则终止整个算法并得到优化连通覆盖子集，否则返回（3）继续优化。

根据上述算法流程，可得算法流程图如图5所示。

图5 群混合算法流程图

4 仿真实验

4.1 仿真环境

为验证本文提出的算法的有效性，利用蚁群算法（ACO）与本文的群混合智能算法（HSIAO）进行对比。在搜索过程中，由于蚁群算法与改进后群混合智能算法都含有一定的随机性，为减小随机性带来的误差，在本文每组实验中，每个算法都执行25次独立试验，分别取各算法的平均值（除不尽的平均值保留二位小数）作为最后的实验结果。其中实验中的控制参数设置为蚂蚁数m=5，β=2，ρ=ζ=0.1，w0，w1，w2= 1/3，w3=|CF|，最大迭代次数max=10，阈值c=1。仿真结果表明，本文所提出的算法效果上优于蚁群算法。

4.2 实验结果分析

4.2.1 优化连通覆盖子集数的均值比较

实验在50 m×50 m目标监测区域进行。随机部署大量SR和SK节点。表1汇总了网络的设置，包括|SR|和|SK|数量，传感器感知半径rs，收集器收集半径rt，收集器传输半径Rt，理想连通覆盖子集数量的上界值|CF|，两种算法寻优的平均优化连通覆盖子集数。一共进行了十组不同的实验，其中每组的节点规模不同。从表1中可以看出，在|SR|=100、|SK|=50、rs=15、rt=18、Rt=32、|CF|=9相同情况下，本文算法平均找出了9层连通覆盖子集，而蚁群算法只找出6.83层连通覆盖子集，没能达到理想连通覆盖数量的上界值|CF|。同时由整个列表结果可以得知，本文算法明显优于蚁群算法，并且在迭代次数相同条件下，本文算法比蚁群算法更早找到全局最优值。

表2 两种算法构建优化连通覆盖子集数的均值比较

为了更加直观说明改进后算法优越性，本文画出了在|SR|=100、|SK|=50、rs=15、rt=18、Rt=32、|CF|=9参数下，改进后的群混合智能算法完成10次迭代后，找到的9层连通覆盖子集在目标区域内满足覆盖约束、收集约束、连通约束效果示意图，如图6和图7所示。其中图中方框代表50 m×50 m的目标监测区域，●表示传感器节点，▲表示收集器节点，图中编号0-99是不同传感器节点，100-149是不同收集器节点，其中以传感器节点为圆心和rs为半径所画的深色圆代表传感器节点对目标区域监测效果，以收集节点为圆心和rt为半径所画的浅色圆区域代表收集节点对传感器节点信息收集效果。从图6（a）～（i）子图中可以看出，每一组子图的传感器节点都能对目标监测区域实现完全覆盖，且全部传感器节点至少处于一个收集节点的收集半径内，实现了收集节点对传感器节点信息的收集。从图7（a）～（i）子图中可以看出，以收集节点为圆心和Rt为半径所画的圆区域，每个子图中任意两个收集器节点能进行传输通信，即形成了一个无线连通网络，同时9层连通覆盖子集节点冗余度极少，可以看出本文算法的有效性。

图6 覆盖收集子集示意图

图7 连通子集示意图

4.2.2 鱼群拥挤度对实验结果影响分析

为了说明鱼群拥挤度对本文提出的群混合算法实验结果的影响，在相同的仿真条件下，分别对蚁群算法和本文提出的群混合算法进行了寻优值收敛性分析。图8（a）、（b）分别在|SR|=100，|SK|= 50，rs=15，rt=18，Rt=32和|SR|=800，|SK|=150，rs=8，rt= 18，Rt=30的条件下，所得到的结果。横坐标代表迭代次数，本文最大迭代次数设为10，纵坐标表示满足连通覆盖的平均优化子集数S。对图8的曲线分析可知，在算法初期，本文提出的群混合算法在鱼群拥挤度作用下，能够更快地跳出局部最优，这表明该算法增强了全局寻优能力，并且在相同迭代次数下，本文提出的群混合算法找到的平均子集数较蚁群算法多，更说明本文算法寻优效果明显。

4.2.3 节点冗余分析

为了说明本文提出的关键域法去冗余节点的有效性，在算法前期利用蚁群算法构建子集解，而在算法后期分别应用关键域法（KFM）、圆周覆盖算法（CCA）判断冗余节点。图9所示是在|SK|=100，rs=10，rt=20，Rt=32的条件下，部署不同传感器节点数a所产生平均冗余节点的个数变化，即是平均冗余节点数b。

图8 鱼群拥挤度对实验结果影响分析

图9 部署传感器数与节点冗余数比较

图9中横坐标表示随机部署不同传感器节点数，纵坐标表示不同传感器节点数下，构建子集出现的平均冗余节点数量。从图9可以看出蚁群算法构建子集存在大量冗余节点，在应用去冗余算法后，可有效地减少冗余节点，对比图中各曲线，可以看出关键域法去冗余效果比圆周覆盖算法更优。

5 结论

针对异构无线传感器网络中多层覆盖问题，本文结合了基本鱼群算法和蚁群算法各自的优点，将鱼群拥挤度引进到蚁群算法中，防止算法早期陷入局部最优，该混合智能算法提高了算法的收敛速度，增强了全局寻优能力；同时提出的关键域法去冗余，提高了节点利用率，延长了网络生命周期。通过对理论的分析以及实验的仿真，结果都表明该方法模型的有效性。

［1］Dietrich I，Dressler F.On the Lifetime of Wireless Sensor Net⁃works［J］.ACM Trans Sensor Networks，2009，5（1）：1-37.

［2］毛科技，陈庆章.基于改进蚁群算法的无线传感器网络栅栏覆盖优化研究［J］.传感技术学报，2015，28（7）：1058-1065.

［3］杜晓玉，孙力娟.异构无线传感器网络覆盖优化算法［J］.电子与信息学报，2013，36（3）：696-701.

［4］陈业钢，徐则同.无线传感器网络最小连通覆盖的节能算法［J］.计算机仿真，2014，31（3）：324-350.

［5］张蕾.无线传感器网络中多重覆盖算法的研究［J］.传感技术学报，2014，27（6）：802-806.

［6］Zhu C，Zheng C L.A Survey on Coverage and Connectivity Issues in Wireless Sensor Networks［M］.Journal of Network and Comput⁃er Applications，2012，35（2）：619-632.

［7］Slijepcevic S，Potkonjak M.Power Efficient Organization of Wire⁃less Sensor Networks［C］//IEEE International Conference on Com⁃munication，2001，2：472-476.

［8］Hu X M，Luo X N.Hybrid Genetic Algorithm Using a Forward En⁃coding Scheme for Lifetime Maximization of Wireless Sensor Net⁃works［J］.IEEE，2010，14（5）：766-781.

［9］Attea B A，Khalil E A.A Multi-Objective Disjoint Set Covers for Reliable Lifetime Maximization of Wireless Sensor Networks［J］.Wireless Pers Commun，2015，81（2）：819-838.

［10］Lin ，Zhang J.An Ant Colony Optimization Approach for Maxi⁃mizing the Lifetime of Heterogeneous Wireless Sensor Networks［J］.IEEE Transactions on Systems，2012，42（3）：408-420.

［11］Zhong Y P，Huang P W，Wang B.Maximum Lifetime Routing Based on Ant Colony Algorithm for Wireless Sensor Networks［C］//IET Conference on Wireless，Mobile，Sensor Networks，Shanghai，2007：789-792.

［12］Chartrand G，Zhang P.Introduction to Graph Theory［M］.The People’s Post Telecommun，2006：140-156.

［13］Liao T，Socha K.Ant Colony Optimization for Mixed-Variable Op⁃timization［J］.IEEE Transactions on Evolutionary Computation，2014，18（4）：503-518.

［14］Huang Y Y，Li K Q.Coverage Optimization of Wireless Sensor Network Based on Artificial Fish Swarm Algorithm［J］.Applica⁃tion Research of Computer，2013，30（2）：554-556.

［15］Xing G L，Wang X R.Integrated Coverage and Connectivity Con⁃figuration for Energy Conversation in Sensor Network［J］.ACM Transactions on Sensor Networks，2010，1（1）：36-72.

［16］刘潇，张锦.SCCP无线传感器网络自调节圆周覆盖协议［J］.计算机应用研究，2010，24（4）：1407-1409.

［17］杨海雳，赵静.基于Voronoi图的无线传感器网络覆盖算法研究［J］.信息通信，2015，151（7）：28-31.

唐玲艳（1991-），女，华东理工大学硕士研究生，主要研究方向为无线传感器网络；

吴 雪（1957-），通信作者，女，副教授，硕士研究生导师，先后任教于华中科技大学、天津大学和华东理工大学。主要研究方向为计算智能与自然计算，图论及通信网系统优化，无线传感器网络，wuxue@ecust.edu.cn；

吴 喆（1991-），男，华东理工大学硕士研究生，主要研究方向为无线传感器网络。

罗小娟（1974-），女，博士，讲师，主要研究方向为网络优化，物联网及无线传感器网络。

Hybrid Swarm Intelligence Algorithm Optimizing Heterogeneous Wireless Sensor Network LifeTime*

TANG Lingyan，WU Xue*，WU Zhe，LUO Xiaojuan
（School of Information Science and Engineering，East China University of Science and Technology，Shanghai 200237，China）

In order to optimize the lifetime of heterogeneous wireless sensor network，the key methodology is based on finding more connected covers subsets.This paper proposes to form the target evaluation function from coverage constraints，collection constraints and connectivity constraints.According to the model，this paper introduces the fish crowded degree into the ant colony algorithm to prevent ant colony algorithm from local convergence at the be⁃ginning of the algorithm.The experiments show that the improved algorithm is better than general ant colony algo⁃rithm in global search ability and convergence speed.And as for the ant colony algorithm in building a subset that exists a number of redundant nodes，this paper puts forward the key field method（KFM）to judge redundant nodes in each subset and constructs new subsets by the use of the redundant nodes.Not only it improves the utilization effi⁃ciency of nodes，but also extends the lifetime of heterogeneous networks.

heterogeneous wireless sensor network；network lifetime；connected covers subsets；ant colony algo⁃rithm；fish crowded degree；key field method

TP212.9；TP18；TP393

A

1004-1699（2016）11-1759-09

EEACC：6150P；6210C 10.3969/j.issn.1004-1699.2016.11.022

项目来源：上海市自然科学基金项目（15ZR1408700）

2016-03-28 修改日期：2016-07-27