基于QS-ML-PMHT的多目标无源协同定位方法*

郭云飞，滕方成，曾泽斌

（1.杭州电子科技大学自动化学院通信信息传输与融合技术国防重点学科实验室，杭州310018；2.浙江理工大学机械与自动控制学院，杭州310018）

基于QS-ML-PMHT的多目标无源协同定位方法*

郭云飞1*，滕方成1，曾泽斌2

（1.杭州电子科技大学自动化学院通信信息传输与融合技术国防重点学科实验室，杭州310018；2.浙江理工大学机械与自动控制学院，杭州310018）

针对目标个数未知时无源协同定位系统低可观测目标的航迹起始及维持问题，提出一种基于拟蒙特卡罗模拟退火极大似然概率多假设的双基站多目标无源协同定位方法。首先，建立双基站无源协同定位系统数学模型。其次，提出基于极大似然概率多假设的多目标无源协同定位航迹起始算法，通过假设法确定目标个数，并首次利用拟蒙特卡罗模拟退火算法解决极大似然概率多假设中多目标的优化求解问题，以提高多目标检测跟踪性能。最后，通过滑窗法实现航迹维持。仿真结果表明，所提方法能够有效解决目标个数未知时双基站无源协同定位系统低可观测目标的航迹起始及维持问题。

无源协同定位；极大似然概率多假设；拟蒙特卡罗；模拟退火；低可观测目标

无源协同定位［1］PCL（Passive Coherent Location）指的是雷达本身不发射电磁波，借助非合作外辐射源（如手机通信基站［2］，数字电视信号基站［3］等）发射的电磁波来检测跟踪目标。与传统的有源雷达［4］相比，PCL系统体积小，抗干扰能力强，自身静默，具有较强的生存能力。除此外，PCL系统利用双基站的空间分布性大幅提高了系统对低空和隐身目标的探测性能，受到了国内外学者的广泛关注［1-3］。

由于PCL系统中被检测目标的信噪比很低且目标个数未知，如何利用PCL系统实现目标个数未知时低可观测目标的航迹起始及维持［5］是亟待解决的关键问题之一。文献［6］在目标个数已知时对目标的航迹维持做了研究。文献［7］基于主动雷达系统研究分析了多目标的航迹起始及维持问题。文献［8-9］重点研究了低信噪比情况下单目标的检测跟踪问题，不适用于多目标场景。文献［10］假设目标航迹起始状态为已知，重点在于航迹维持。为解决目标个数未知时PCL系统低可观测目标的航迹起始及维持问题，本文提出一种基于拟蒙特卡罗模拟退火［11］极大似然概率多假设［12］QS-ML-PMHT（Quasi-Monte Carlo Simulated Annealing Maximum Likeli⁃hood Probabilistic Multi-Hypothesis）的多目标无源协同定位方法。该方法基于双基站PCL系统的检测跟踪数学模型，通过对多帧测量进行积累，构建对数似然函数，通过假设法确定目标个数，并利用拟蒙特卡罗模拟退火技术优化求解，以实现航迹初始化。最后采用滑窗［13］批处理技术，进行航迹维持。本文剩余章节安排如下：第1节建立了双基站PCL系统检测跟踪的数学模型。第2节提出了基于QS-MLPMHT的双基站多目标无源协同定位算法，第3节仿真分析所提方法的性能，第4节是总结。

1 问题描述

考虑图1所示的双基站PCL系统，Tx表示外辐射源，Rx表示接收站，Oj表示第 j个目标，表示Oj与Rx间的距离，表示Oj与Tx间的距离，dRT表示Rx与Tx间的距离，θj表示Rx与Tx、Oj间的夹角。Rx由监控天线和参考天线组成，其中监控天线接收由Tx发射且经Oj反射的信号，参考天线接收Tx发射的直达信号。通过比较回波信号和直达信号，实现Oj的无源定位。

图1 双基站PCL系统示意图

记Oj在第k帧的状态为，其中和分别表示Oj在x,y方向的位置和速度。假设在测量时间内，Oj近似做如下匀速直线运动：

为实现低可观测多目标的航迹起始，通常做如下基本假设［12］：（1）不同帧之间的测量相互独立；（2）每帧的测量集中包含任意个源于目标的测量，每个目标的检测概率为Pd，其余测量为杂波；（3）杂波在测量空间Ω内服从均匀分布，杂波个数服从参数为λ的泊松分布。基于如上假设，PCL系统中低可观测多目标的测量模型为：

式中，zki表示第k帧第i个测量。表示目标状态在测量空间Ω中的非线性映射，其中：

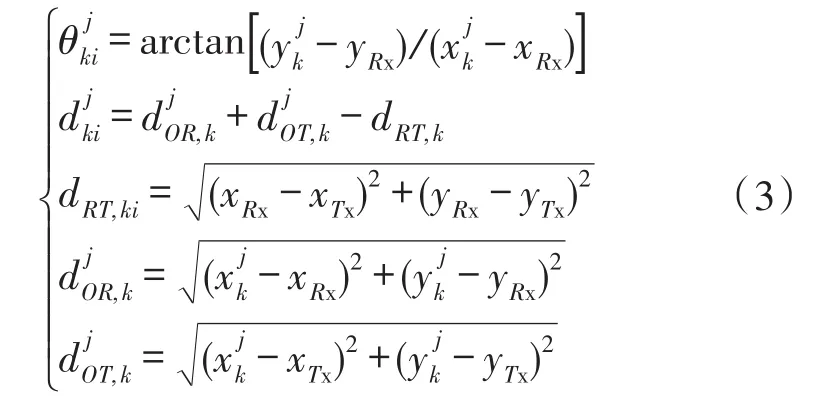
式中，[xRx,yRx]和[xTx,yTx]分别表示Rx和Tx的位置。若测量源自Oj，则测量噪声Wki服从零均值高斯分布，，N表示高斯分布，σθ和σd表示方位角和距离差的测量标准差。若测量为杂波Θki，则假设其均匀分布在测量空间Ω=Ωθ×Ωd内，其中Ωθ和Ωd分别表示的测量范围。假设第k帧测量个数为mk，记第k帧测量集合为，则K帧测量集合记为。双基站无源协同定位目的是利用Z1:K确定目标个数并检测Oj是否出现及估计其状态。

2 QS-ML-PMHT

QS-ML-PMHT算法的基本思想是首先通过对Rx获取的测量信息多帧积累，构建对数似然比LLR（Log Likelihood Ratio），通过假设法确定目标个数，然后利用QS优化算法求解LLR的最优状态估计，实现目标航迹初始化，最后采用滑窗法实现目标航迹维持。

2.1 LLR的构建

根据PCL测量模型（2）和全概率理论［12］，当目标个数为J时，则K帧测量集合Z1:K的LLR为：

式中，π0表示测量为杂波的先验概率，πj表示测量源自Oj的先验概率，且，V表示测量空间大小，表示源自Oj的测量的似然函数：

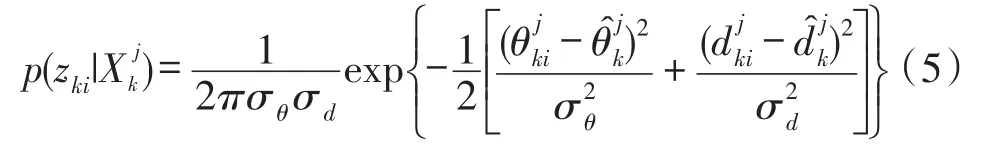
2.2 假设法求解目标个数

在目标个数未知情况下，需确定目标个数后才能进行LLR的优化求解过程，已知目标最多有Jmax个，假设法为首先假设目标有J=1,2,…,Jmax个，根据式（4）分别求出对应的对数似然函数值，则目标实际个数Jtrue为：

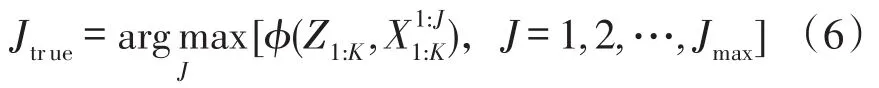
2.3 LLR的优化求解

在ML-PMHT框架下，目标状态估计问题转化为求解如下优化问题：

当目标个数为J时，目标状态向量变成4J×1的向量。能否快速有效获得全局最优解，直接影响ML-PMHT的算法性能。网格搜索GS（Grid Search）法在优化目标状态时，计算量随着目标个数增加呈指数倍上升，当有多个目标时，计算量很大，GS无法得到实际应用。为了提高ML-PMHT的优化性能，控制多目标优化的计算量，改善目标检测跟踪结果，本文提出基于QS的优化求解方法，实现步骤如下：

Step 1 在对数似然函数解空间内采用基于Halton序列的拟蒙特卡罗方法产生分布更加均匀的M个状态采样点，解空间内状态采样点的集合为：

Step 3 设温度初始值为t0，温度tξ时的当前解为，进行第le+1次搜索，其中0≤le＜Le，Le为 Markov链长。

②计算转移概率P：

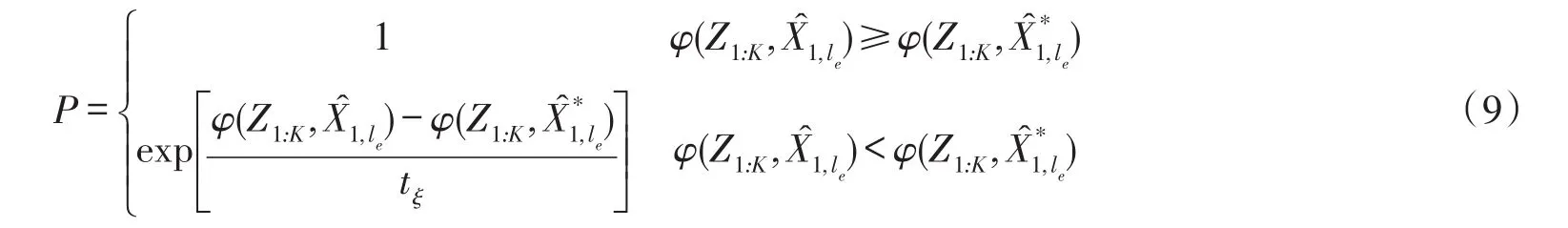
③当le＜Le时，重复Step 3，否则进入Step 4。

Step 4 当tξ＜tmin时，终止本算法，否则进入Step 5，其中tmin为温度停止下限。

Step 5 产生新的温度tξ+1=τ·tξ，进入Step 3重新搜索，其中τ为温度衰减参数。

2.4 滑窗法实现航迹维持

滑窗法即当Rx获取新一帧的测量信息后，移除W帧测量中的第一帧，将最新获得的测量作为滑窗中的第W帧，根据测量集Zk:k+W-1来估计目标第k帧的状态：

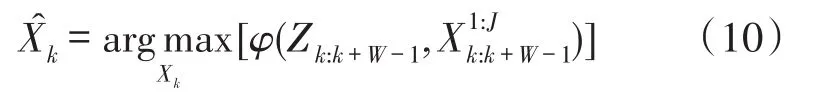
3 仿真分析

本节选择数字电视广播作为外辐射源［14］，通过两个典型场景，对比同类算法GS-ML-PMHT和基于遗传算法GA（Genetic Algorithm）的GA-ML-PMHT来说明所提方法的有效性。场景1：目标不存在；场景2：目标中途进入并离开探测区域。场景参数如下：探测时间70 s，测量间隔1 s，Rx的位置为［0 km，0 km］，Tx的位置为［0 km，10 km］，Ωθ=［0.17 rad，1.40 rad］，Ωd=［0.01 km，20 km］，σθ=0.02 rad，σd=0.05 km，Pd=0.9，λ=5。算法参数如下：t0= 60℃，τ=0.8，tmin=20℃，Le=100，W=20，M= 10 000，V=2.4×107，π0=0.85，π1=π2=π3=0.05；GS-ML-PMHT算法状态向量每个维度划分4格，步长为10 m；GA-ML-PMHT算法调用Matlab工具箱GA函数，参数为：种群大小20，创建初始种群函数为Constraint dependent，初始种群向量为［0；1］，交叉概率为0.8，遗传代数100，变异率为0.2，算法停止下界1×10-6。计算机参数如下：Intel（R）Core（TM）i5 CPU M480@2.67 GHz，内存2.00 GB，32位操作系统；仿真软件为MATLAB2013a。

场景1：目标不存在

图2（a）、2（b）给出了目标不出现情况下，速度和位置分别取真值时，位置解与速度解的分布。可以看出存在多个位置解和速度解，经门限检测后［12］，判定目标不存在。

图2 目标不存在时LLR解的分布

场景2：目标出现

针对已知目标个数最大值Jmax=4，目标个数未知的场景进行验证所提算法的有效性。目标实际个数Jtrue=3，目标第21 s出现，第41 s消失，出现20 s。目标1的初始状态为［5 km，0.2 km/s，4 km，0.1 km/s］，目标2的初始状态为［6 km，0.2 km/s，3.5 km，0.2 km/s］，目标3的初始状态为［6 km，0.1 km/s，3 km，0.05 km/s］。图3（a）、3（b）分别给出了角度和距离差的原始测量。图4（a）、4（b）分别给出了目标存在情况下，LLR当速度和位置取真值时，位置解和速度解的分布。可以看出目标存在时，经门限检测后，目标的位置解和速度解是唯一的。

图3 传感器原始测量

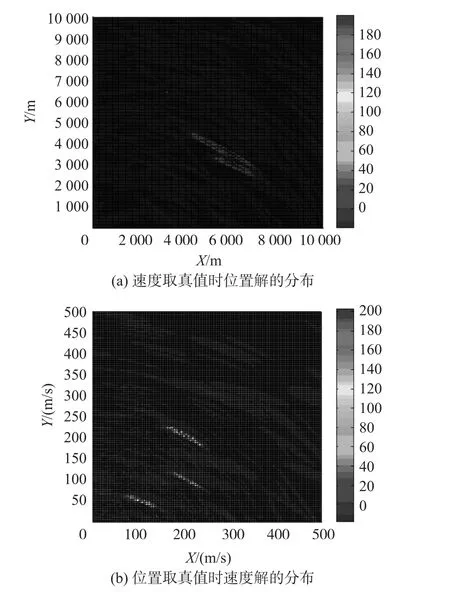
图4 目标存在时LLR解的分布

图5给出了不同目标个数时所对应的LLR值，通过假设法可知当目标个数为3时LLR值最大，则确定探测周期内共有3个目标。图6给出了QS-MLPMHT算法的跟踪效果图，从图6可知所提算法能有效处理多目标的检测跟踪问题。

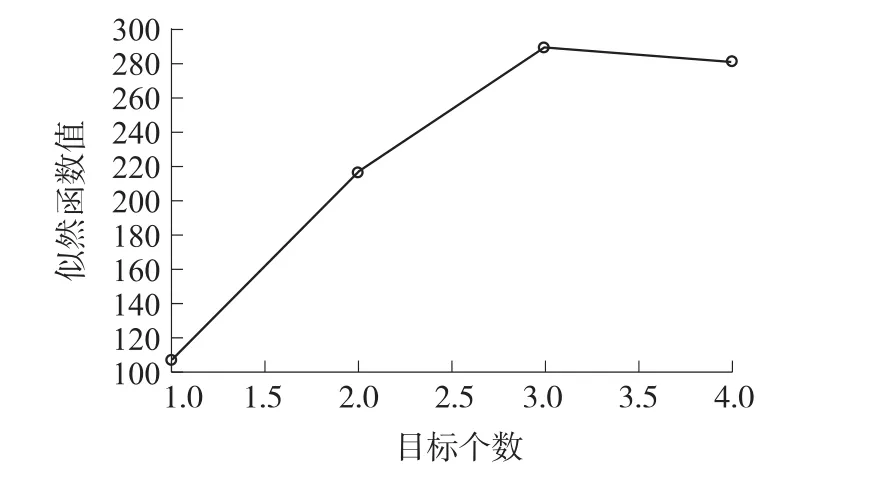
图5 不同目标个数时相对应LLR值

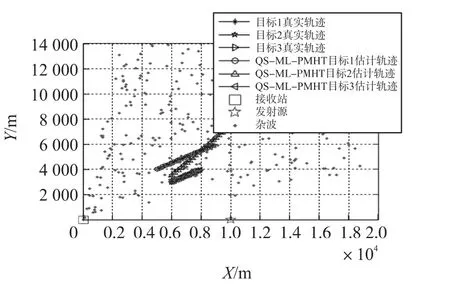
图6 QS-ML-PMHT算法跟踪效果图

进一步，该场景下仿真对所提方法与同类算法GS-ML-PMHT、GA-ML-PMHT进行了比较。图7（a）和7（b）分别给出了3种算法的距离估计RMSE和速度估计RMSE，表1给出了不同目标个数时3种算法的单次耗时。相比GS-ML-PMHT算法，所提算法减小了目标速度估计误差，增加了目标位置的估计误差，极大缩短了单次耗时；相比GA-ML-PMHT算法，所提算法牺牲少量实时性来较大提高目标估计精度。本文所提QS-ML-PMHT算法适用于多目标情况下跟踪精度较高，实时性较强的场景。

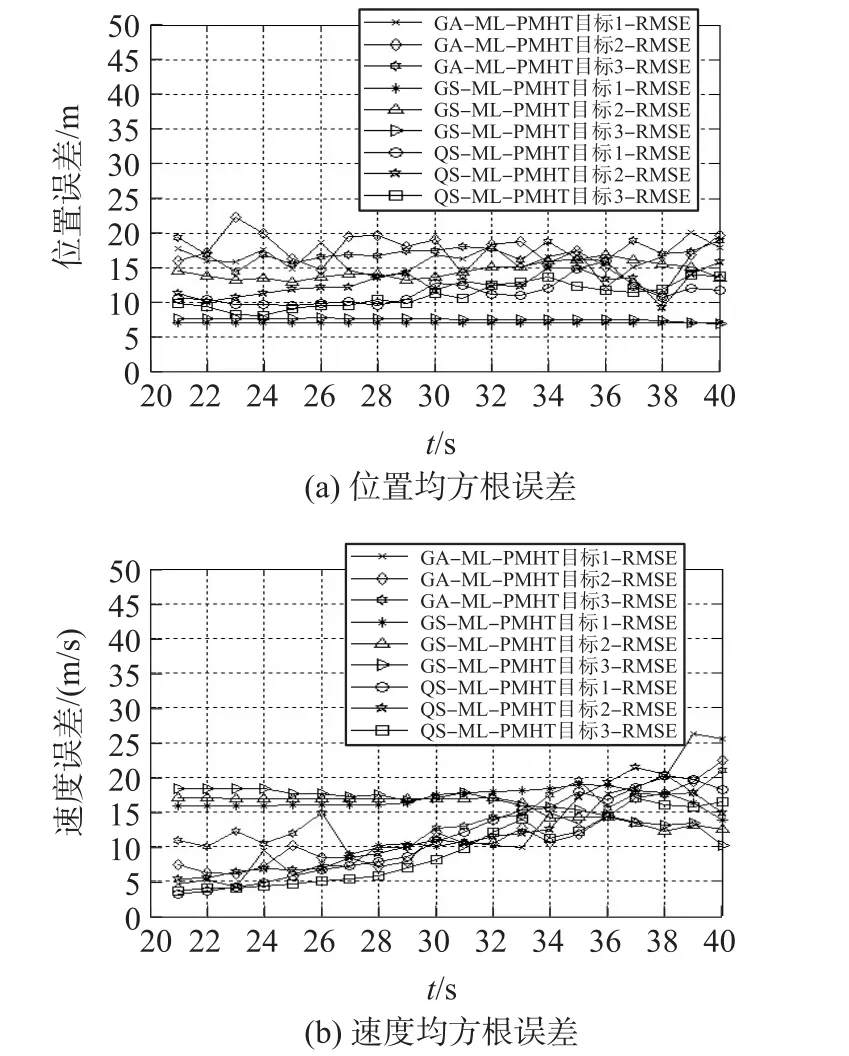
图7 3种算法的跟踪误差

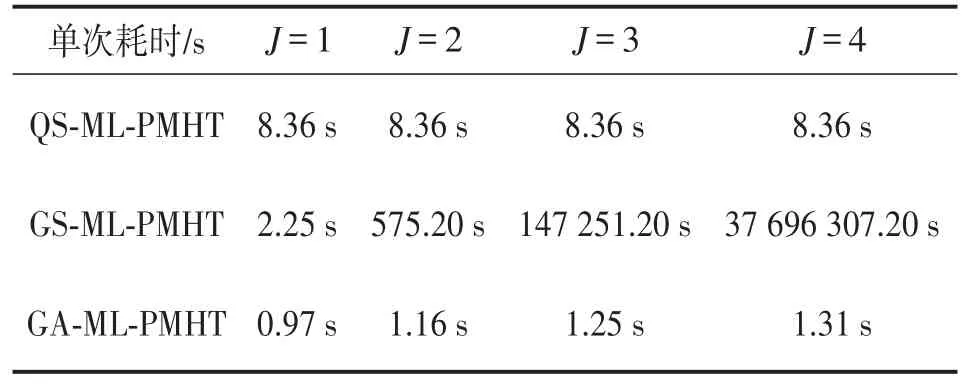
表1 不同目标个数时三种算法的单次耗时

表2和表3分别给出了不同滑窗宽度和不同QMC样本数时QS-ML-PMHT算法的跟踪误差，从表2和3可知，随着滑窗宽度和QMC样本数的增加，所提算法跟踪误差下降，算法跟踪精度提高。

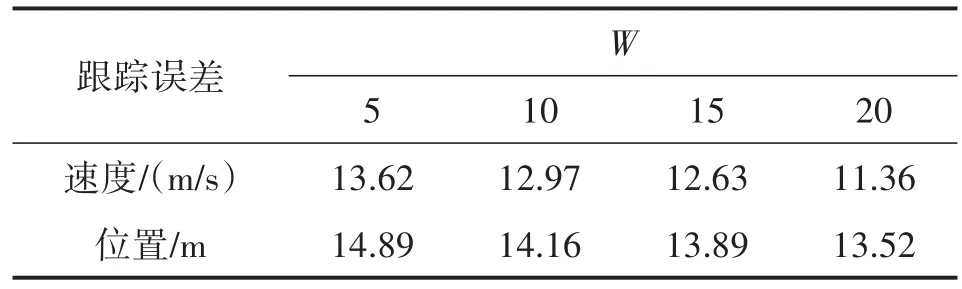
表2 不同滑窗宽度时QS-ML-PMHT跟踪误差

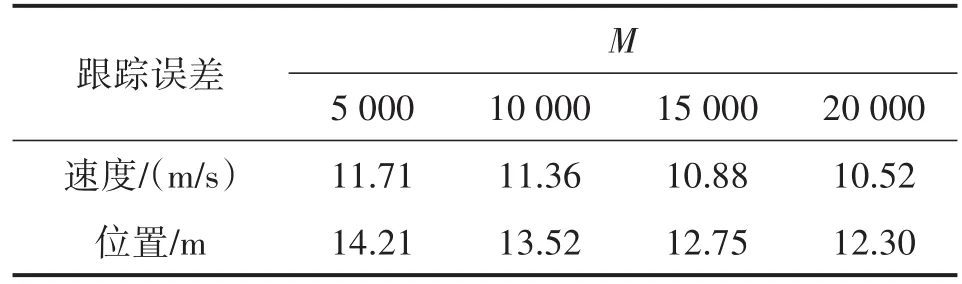
表3 不同QMC样本数时QS-ML-PMHT跟踪误差

4 结论

本文针对双基站PCL系统下低可观测目标检测跟踪问题，提出了QS-ML-PMHT算法。经仿真分析，与同类算法相比，所提算法能有效地减小计算量，提高实时性。接下来的工作将重点研究杂波环境下的PCRLB推导与分析，以及该算法在门限检测方面的研究。

［1］Fabiola C，Pierfrancesco L.Polarimetric Passive Coherent Loca⁃tion［J］.IEEE Transactions on Aerospace and Electronic Systems，2015，51（2）：1079-1097.

［2］Li H W，Wang J.Particle Filter for Manoeuvring Target Tracking Via Passive Radar Measurements with Glint Noise［J］.IET Radar Sonar Navig，2012，6（3）：180-189.

［3］Mojtaba R，Seyyed M K，Mohammad M N.Data Fusion in MIMO DVB-T-Based Passive Coherent Location［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（3）：1725-1737.

［4］李程，王伟，施龙飞.基于多源信息融合的有源雷达组网方式序贯识别方法［J］.电子与信息学报，2014，36（10）：2456-2463.

［5］李家强，赵荣华，陈金立.基于蚁群相似度加权霍夫变换的航迹起始［J］.传感技术学报，2016，29（4）：552-558.

［6］Mateuse M，Krzysztof K.Two Methods for Target Localization in Multistatic Passive Radar［J］.IEEE Transactions on Aerospaceand Electronic Systems，2012，48（1）：572-580.

［7］Steven S，Peter W，Yaakov B S.ML-PDA and ML-PMHT：Compar⁃ing Multistatic Sonar Trackers for VLO Targets Using a New Multi⁃target Implementation［J］.IEEE Journal of Oceanic Engineering，2014，39（2）：303-317.

［8］齐立峰，惠小平.基于ML-PDA算法的低可见目标跟踪研究［J］.导弹与制导技术，2014，34（1）：27-32.

［9］Domenico C，Peter W，Yaakov B S.Tracking the Tracker from Its Passive Sonar ML-PDA Estimates［J］.IEEE Transactions on Aero⁃space and Electronic Systems，2014，50（1）：573-590.

［10］陈延军，梁新华，潘泉.两级量测更新的粒子滤波检测前跟踪算法［J］.传感技术学报，2015，28（1）：115-120.

［11］Rodrigucz F J，Garcia-Martinez C，Lozano M.Hybrid Meta-Heuris⁃tics Based on Evolutionary Algorithm and Simulated Annealing：Taxonomy，Comparison，and Synergy Test［J］.IEEE Transactions on Evolutionary Computation，2012，16（6）：787-800.

［12］Steven S，Peter W，Yaakov B S.Extreme-Value Analysis for MLPMHT，Part1：Threshold Determination［J］.IEEE Transactions on Aerospace and Electronic Systems，2014，50（4）：2500-2514.

［13］Steven S，Peter W，Yaakov B S.The ML-PMHT Multistatic Track⁃er for Sharply Maneuvering Targets［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（4）：2235-2249.

［14］高志文，陶然，王越.单频网数字电视广播辐射源雷达目标定位算法［J］.兵工学报，2010，31（6）：791-795.

郭云飞（1978-），男，副教授，河北省武安市人，2007年毕业于浙江大学电气学院控制理论与控制工程专业，获博士学位，中国航空学会信息融合分会副总干事，长期从事目标跟踪、弱目标检测、非线性滤波、雷达及声纳数据处理等领域的研究，gyf@hdu.edu.cn；

滕方成（1991-），男，硕士研究生，浙江省杭州市人，就读于杭州电子科技大学控制工程专业，研究方向为无源协同定位，目标检测跟踪，tengtfc@163.com；

曾泽斌（1964-），女，副教授，硕士，研究方向为信息融合，弱目标检测与跟踪，无源协同定位等。

A QS-ML-PMHT Based Multitarget Passive Coherent Location Method*

GUO Yunfei1*，TENG Fangcheng1，ZENG Zebin2
（1.Key Laboratory of Fundamental Science for National Defense-Communication Information Transmission and Fusion Technology，Automation School，Hangzhou Dianzi University，Hangzhou 310018，China；2.School of Mechanical Engineering&Automation，Zhejiang Sci-Tech University，Hangzhou 310018，China）

In order to track very low observable targets with a bistatic passive coherent location system，where the number of targets is unknown，a quasi-Monte Carlo simulated annealing maximum likelihood probabilistic multi-hy⁃pothesis algorithm is proposed.The contributions consist of three aspects.First，the mathematical model for target detection and tracking is established.Second，a maximum likelihood probabilistic multi-hypothesis method is pre⁃sented for multitarget track initialization and determining the number of targets.In addition，the quasi-Monte Carlo simulated annealing algorithm is used for optimization and hence improving the estimation performance.Last，the track maintenance is achieved in a sliding window manner.Simulation results show the effectiveness of the pro⁃posed algorithm.

passive coherent location；maximum likelihood probabilistic multi-hypothesis；quasi-Monte Carlo；simulated annealing；low observable targets

TN958.97

A

1004-1699（2016）11-1753-06

EEACC：7220；7950 10.3969/j.issn.1004-1699.2016.11.021

项目来源：国家自然科学基金项目（61573123）

2016-05-06 修改日期：2016-06-13