基于Hamilton体系的加载边简支矩形薄板稳定性分析

杨洪澜，赵亚荣，郑俊，周涛



基于Hamilton体系的加载边简支矩形薄板稳定性分析

杨洪澜1，赵亚荣2，郑俊3，周涛1

（1. 齐齐哈尔大学 机电工程学院，黑龙江 齐齐哈尔 161006；2. 长春迪瑞医疗科技股份有限公司，吉林 长春 130000；3. 江苏大学 能源与动力工程学院，江苏 镇江 212013）

在板微弯曲最小势能变分原理的基础上，选用状态变量和对偶变量，导向一般变分原理．经过变分运算，得出全状态变量表示的微分方程组．采用分离变量法得到本征值方程，给出了本征值方程的解，导出加载边简支矩形薄板挠度的级数表达式．可以根据各种边界条件建立板稳定性问题方程．

Hamilton体系；弹性薄板；稳定性；分离变量法

近年来，Hamilton体系成为一个重要研究领域．钟万勰教授[1]首先把Hamilton体系下的对偶变量方法引入到弹性力学问题中，该方法的核心在于方程的正则化，将欧氏空间问题转化到辛空间．文献[2]揭示了多门力学学科具有辛对偶变量体系这一共同数学基础，指出保守体系的各种近似分析皆应保辛．姚伟岸[3]等研究了薄板弯曲问题的分离变量及辛本征函数展开的直接解析法．钟阳[4]在Hamilton体系下，利用辛几何方法给出了四边固支矩形薄板自由振动问题的解析解．胡志强[5]将Hamilton体系引入到比例边界有限元方法中，得到了边界刚度阵所满足的黎卡提方程，采用精细积分等方法予以求解．鲍四元[6]建立了Mindlin的Hamilton正则方程，采用直接解法得出了对边简支矩形板弯曲问题的解析解．李俊永[7]等通过在Hellinger-Reisser广义势能中引入应变的非线性项，计入剪切变形的影响，导出了Hamilton体系下的屈曲基本方程．但在求解临界载荷时，仍假设一个屈曲函数，将其代入屈曲基本方程．可以看出，Hamilton体系在弹性力学的各个课题中取得了较好的应用．自从钟万勰教授在文献[1]中指出，弹性力学新体系在弹性稳定性方面也可以有所发挥以来，这方面的研究成果很多．本文通过在能量泛函中引入拉格朗日乘子以及全状态变量，经过变分运算导向Hamilton体系，用分离变量法得到对边简支板挠度函数的级数表达式．然后通过边界条件确定临界载荷．与传统方法相比，本文方法不必事先假定挠度函数，因而富于理性．

1 单向受压矩形薄板稳定性方程在Hamilton体系中的表示

加载边简支矩形薄板的力学简图见图1．

图1　加载边简支矩形板受力简图

相对于基本平衡状态（平面问题），微弯状态的应变能增量是

2 用分离变量法导出受压薄板微屈的挠度的表达式

代入式（5），得

化简式（10），得

式（11）开方，得

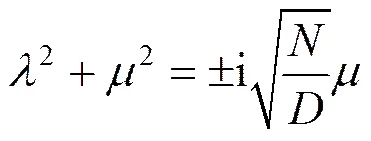
将式（13）代入式（12），得

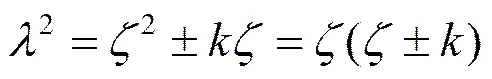
于是得

3 加载边简支的矩形板稳定问题的解

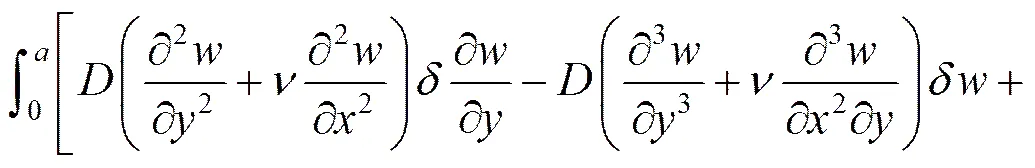
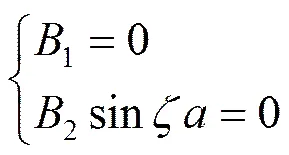
其中

这里

将式（25）代入式（23）的第1式，得

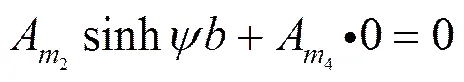
解出

进一步求临界载荷的讨论可见文献[8-9]．应用公式（19）还可求其它约束条件，如加载边简支对边都固支的矩形薄板的临界载荷[10]．

4 结束语

在板微弯状态应变能中引入拉格朗日乘子，得到全状态变量及一般的变分原理．经过变分运算得到哈密顿对偶方程，采用分离变量法得到了挠度表达式的通项．通过求解加载边和非加载边都简支的矩形薄板临界载荷的算例，阐明了Hamilton方法求解薄板稳定性问题的过程．

[1] 钟万勰．弹性力学求解新体系[M]．大连：大连理工大学出版社，1995

[2] 钟万勰．应用力学的辛数学方法[M]．北京：高等教育出版社，2006

[3] 姚伟岸，钟万勰．辛弹性力学[M]．北京：高等教育出版社，2002

[4] 钟阳，李锐，田斌．四边固支矩形薄板自由振动的哈密顿解析解[J]．应用力学学报，2011，28（4）：323-328

[5] 胡志强，林皋，王毅，等．基于Hamilton体系的弹性力学问题的比例边界有限元方法[J]．计算力学学报，2011，28（4）：510-516

[6] 鲍四元，邓子晨．Mindlin 中厚板的辛求解方法[J]．固体力学学报，2005，26（1）：102-106

[7] 李俊永，吕和祥．弹性力学Hamilton体系下的稳定问题[J]．工程力学学报，2007，24（8）：81-85

[8] 黄克智．板壳理论[M]．北京：清华大学出版社，1987

[9] 徐芝纶．弹性力学[M]．北京：高等教育出版社，2006

[10] 胡海昌．弹性力学的变分原理及其应用[M]．北京：科学出版社，1981

Stability analysis of simply supported rectangular thin plate for loaded side based upon Hamilton system

YANG Hong-lan1，ZHAO Ya-rong2，ZHENG Jun3，ZHOU Tao1

（1. School of Mechanical and Electrical Engineering，Qiqihar University，Qiqihar 161006，China；2. Changchun Dirui Medical Technology Co.，Ltd，Changchun 130000，China；3. School of Energy and Power Engineering，Jiangsu University，Zhenjiang 212013，China）

The variational principle for the micro bending plate was derived through the principle of the minimum potential energy with the state variables and dual variables．The differential sate equation set，was then obtained from the variational equation of the generalized functional．The characteristic equation of the equation set was derived by the method of separation of variables，which yields the series solution of the deflection of the thin square plate．Other stability problems of the plate could also be modeled for under different boundary conditions．

Hamilton system；elastic thin plate；stability；separation variable method

1007-9831（2016）11-0036-05

O343

A

10.3969/j.issn.1007-9831.2016.11.010

2016-09-07

江苏省自然科学基金项目（BK20130478）

杨洪澜（1968-），男，黑龙江克山人，讲师，博士，从事超空泡流和弹性理论研究．E-mail：yanghl2020@163.com