双棱镜干涉实验中数据的处理方法

张伦，于建勇，李艳，郭三栋，渠立成



双棱镜干涉实验中数据的处理方法

张伦，于建勇，李艳，郭三栋，渠立成

（中国矿业大学 理学院，江苏 徐州 221116）

双棱镜干涉实验是面向工科大一学生开设的光学实验，其中涉及到较多的数据计算．为了辅助学生在有限的课堂时间内能够测量得到精准的实验数据和正确的实验结果，通过分析3组实验数据，阐述了心算入射光波长的具体步骤和快速排查错误而获得合理数据的方法，旨在培养大学生心算能力、实验技巧以及数据处理技能．

双棱镜干涉实验；心算能力；实验技巧；数据处理技能

随着手机的普及，大学生可谓是人手一部手机，而手机带有许多日常应用工具，这让学生垂手而得计算器．在实验教学中发现，由于大学生随身携带“计算器”，遇到数据计算，即使是很简单的数据，也会首先使用计算器进行计算．如分光计测光栅常数实验涉及到衍射角的计算，实验中测得0级衍射条纹的左游标的读数为280º10´，一级衍射条纹的相应游标读数为276º52´，有学生错误地算出一级衍射角为3º58´．而且，诸如此类的错误屡见不鲜．究其原因，学生使用计算器进行计算时，把“1º”当成“100´”算的．其实，此类数据心算即可，很容易得到正确的结果．

无独有偶，在指导双棱镜干涉实验时也发现同样的问题，明明学生心算就能快速而且准确地得到答案，而学生却按着计算器很慢地给出计算结果，甚至有时还是错误的．这些现象表明，学生的一种能力正在缺失，即心算能力．因此，本文通过双棱镜干涉实验，阐述对大学生心算能力的培养．双棱镜干涉实验是一个比较经典的光学实验，许多高校都在开设．迄今为止，已有多篇关于减小实验误差或提高实验精度[1-4]，改进调节方法或设计参量取值[4-8]，实验仿真[9]以及因材施教[10]的文献报道．本文结合心算能力培养大学生实验技巧和数据处理技能．

1 双棱镜干涉实验原理简介

双棱镜干涉实验原理首先通过双棱镜干涉产生明暗交替的、等间距的干涉条纹（见图１）．其次，在实验中分别测出相邻明（暗）纹的条纹间距，像距以及两实像像点和之间的距离．最后，根据公式以及，计算得到入射光波长．式中：为物距；为透镜的焦距（100 mm）；表示两虚像像点和之间的距离；为虚光源平面中心到屏的中心之间的距离．

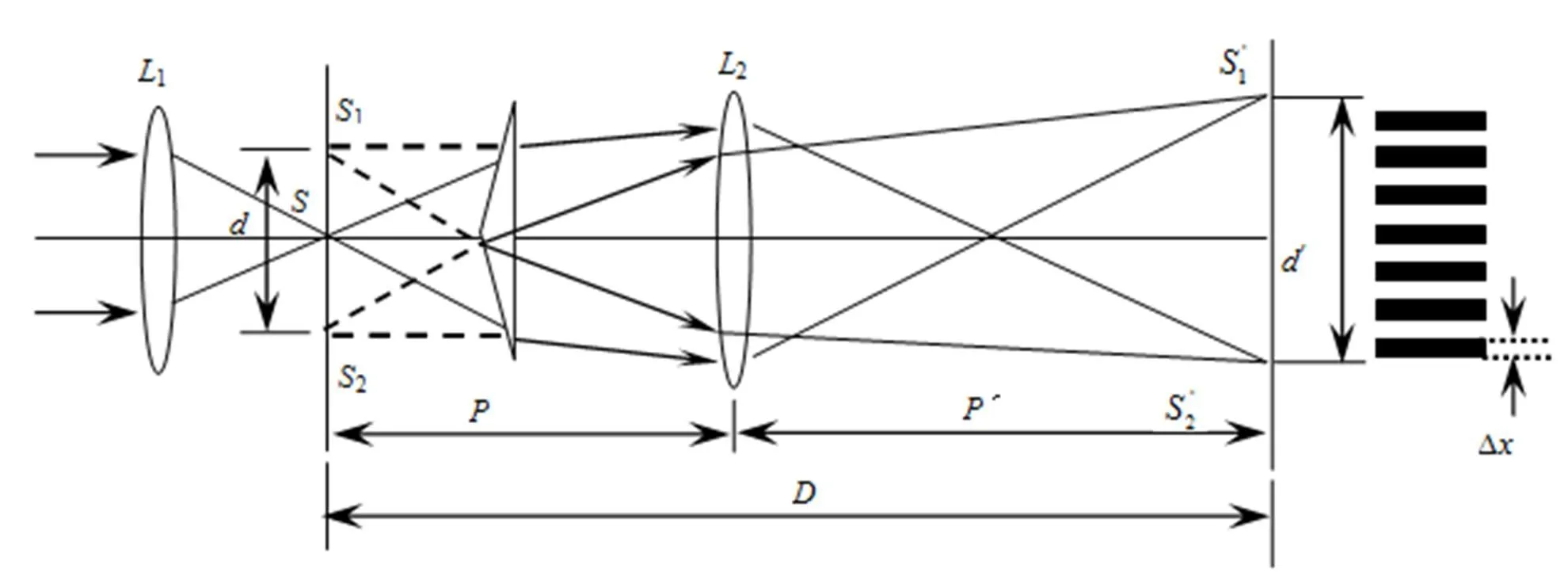
图1 双棱镜干涉实验原理图

2 心算入射光波长的步骤

表1 实验测得的6个暗纹中心的位置 mm

表1 实验测得的6个暗纹中心的位置 mm

暗纹名称x1x2x3x4x5x6 暗纹位置75.95277.71878.94480.61282.03083.486

2.2 统一各物理量的单位

在指导学生实验时，时常发现一些学生忽略考虑各物理量的单位，直接将各量的数值带入公式进行计算而得到错误的结果．例如：学生所测的和常用单位为mm，如mm，mm，而像距常用单位为cm，如cm．时常有学生直接将各量数值带入公式（=100 mm），计算得到像距为负值．因此，课上给学生强调在计算前统一各物理量的单位尤为重要，在此实验中不妨将所有物理量的单位全部统一为mm．

2.3 估算入射光波长

北大赵凯华教授在他的专著[11]中提及：理论物理学家在进行详细计算之前，为了选择和建立恰当的物理和数学模型，需要先粗略地估计各量的大小和各种可能效应的相对重要性，以判断什么是决定现象的主要机制．同理，在物理实验中对待测量进行半定量的估算，可以初步判断实验结果的正误，辅助实验有序地进行．实验表明，在双棱镜干涉实验中，估算入射光波长可以有效地提高实验效率．

就测量数据进行说明，本实验所用红色激光波长为650 nm，考虑到误差存在，一般要求学生测试光波长应该落到可见光波段（390~760 nm），而测量结果超出此范围的要求其重新测量．大量实验数据和计算结果表明，物距和虚光源平面中心到屏的中心之间的距离都可以按和进行估算，因此可将mm和mm代入估算公式计算得到：

3 分析3组实验数据以示心算能力和实验技巧的培养

3.1 数据分析1

从表1数据估算得到的光波长偏小，精确计算各量数值，进而计算光波长．

虽然光波长精确计算结果（419.1 nm）比估算结果（360 nm）大59 nm，但仍比真实值偏小很多．究其原因，的数值和的数值大小不匹配．大量数据表明，的数值和的数值大小在一定范围内具有匹配关系，当然学生不知道这一点，但教师可以适当指导学生明白这一规律．如果数值正确，则测量值偏小；反之，如果数值正确，则测量值偏小．根据数据规律，本次实验测量错误致使错误的可能性不大．本着快捷的原则，应该先假设数值正确，然后检查正确与否，因为的测量比方便快捷很多．如果测量无误，再检查正确与否．总之，排查错误时应该有优先次序．

3.2 数据分析2

表2 实验测得6个暗纹中心的位置 mm

表2 实验测得6个暗纹中心的位置 mm

暗纹名称x1x2x3x4x5x6 暗纹位置88.76390.30791.56093.67295.62496.866

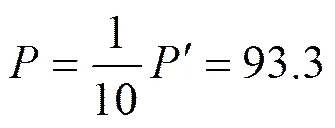
虽然估算光波长（850 nm）比精确计算结果（977.7 nm）小约128 nm，但测试结果偏大的结论仍是对的．究其原因，仍然是的数值和的数值大小不匹配．如果数值正确，则测量值偏大；反之，如果数值正确，则测量值偏大．而因测量错误导致错误的可能性不大．排查错误的优先次序同上，不再赘述．

3.3 数据分析3

表3 实验测得6个暗纹中心的位置 mm

表3 实验测得6个暗纹中心的位置 mm

暗纹名称x1x2x3x4x5x6 暗纹位置97.48496.35295.15094.43093.23091.996

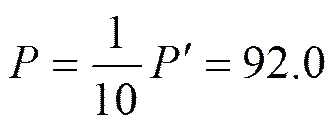
估算光波长（520 nm）比精确计算结果（616.7 nm）小约97 nm．虽然本次光波长计算结果是合理的，但仍有一处结果值得推敲．根据实验现象和规律：干涉条纹的宽度与虚光源平面中心到屏的中心之间的距离有关，（）值越大，越小．根据数据分布规律，纵观数据分析1和数据分析2，的测量值可能偏小，所以应该检查的测量是否有误．

由3组数据分析结果可见，用文中所述的心算方法估算得到的波长一般比精确计算结果偏小，但所估算测量波长的大小趋势（偏大、偏小或合理）是正确的．因此，可以辅助学生快速检查实验结果正确与否．

4 结论

本文基于双棱镜干涉实验，首先通过一组实验数据，阐述了心算入射光波长的具体步骤：准确计算相邻明（暗）纹间距；统一各物理量的单位；估算入射光波长．最后，通过分析3组实验数据，结合心算技巧讨论了快速排查错误而获得合理数据的技巧与方法．

[1] 王明吉，张利巍，王晓莉．双棱镜干涉４种实验方法的研究与探讨[J]．物理实验，2008，28（4）：25-27

[2] 陈华，李艳，渠立成．基于Mathematica 改进双棱镜干涉实验[J]．物理实验，2015，35（8）：25-27

[3] 梁雄，赖国忠．双棱镜干涉实验测量方法的改进[J]．物理实验，2013，33（12）：24-26

[4] 韩修林，孙梅娟．双棱镜干涉实验的研究[J]．安庆师范学院学报：自然科学版，2008，14（3）：96-99

[5] 王秀敏．浅谈“双棱镜干涉实验”的距离参数[J]．大学物理实验，2007，20（3）：52-53

[6] 张胜海，吴天安，张岩．双棱镜干涉实验中调节方法的改进[J]．大学物理实验，2016，29（4）：59-61

[7] 李光明，王宝莲．双棱镜干涉实验中的参量取值研究[J]．物理与工程，2011，21（1）：28-33

[8] 葛松华，唐亚明．菲涅尔双棱镜干涉实验中双棱镜两种放置方法的讨论[J]．大学物理实验，2012，25（1）：35-37

[9] 董键，崔秀芝．用光线追迹方法仿真菲涅尔双棱镜干涉实验[J]．物理实验，2013，33（11）：32-36

[10] 陈余行，陈良雷．双棱镜干涉中虚光源的测量方法对实验的影响[J]．大学物理实验，2014，27（1）：32-33

[11] 赵凯华．定性与半定量物理学[M]．北京：高等教育出版社，20008：100-154

Data processing technique in biprism interference experiment

ZHANG Lun，YU Jian-yong，LI Yan，GUO San-dong，QU Li-cheng

（School of Sciences，China University of Mining and Technology，Xuzhou 221116，China）

Biprism interference experiment which can be categorized as optic experiments are offered for freshmen in engineering．It involves many datum calculation．Therefore，in order to help students to obtain accurate experimental datum and correct results in limmited class teaching hours，analysized three groups of experimental datum and discussed how to perform mental arithmetic for incident light wavelength in detail and get correct datum quickly through mistake investigation．It aims at studying the cultivation of mental arithmetic ability，experimental skills and data processing technique for university students．

biprism interference experiment；ability of mental arithmetic；experimental skill；data processing technique

1007-9831（2016）11-0084-04

O436∶G642.0

A

10.3969/j.issn.1007-9831.2016.11.023

2016-10-08

国家自然科学基金项目（11404391）

张伦（1978-），女，安徽寿县人，讲师，博士，从事纳米发光材料和纳米半导体催化剂的研究．E-mail：zhanglun05@163.com