某型号激光陀螺温度补偿技术的应用研究

张　震，张　林，陈善秋，杜少军

（北京航天时代激光导航技术有限责任公司，北京100094）

某型号激光陀螺温度补偿技术的应用研究

张震，张林，陈善秋，杜少军

（北京航天时代激光导航技术有限责任公司，北京100094）

温度是影响激光陀螺输出漂移的主要因素之一。在高精度的激光捷联惯导系统中，建立激光陀螺的温度误差模型具有十分重要的意义。在大量实验的基础上，研究了激光陀螺在不同环境温度下的漂移特性，提出了一种将静态温度模型与动态温度模型分开建模的方法。环境适应性实验验证该方法建立的温度补偿模型对于缓变温度环境与快速温变环境均适用。最后通过实际导航实验验证了该模型具有工程实用性。

激光陀螺；温度补偿；静态温度误差模型；动态温度误差模型

0 引言

机抖激光陀螺是基于Sagnac效应的光学陀螺，以其自身诸多优点［1］成为捷联惯导系统的理想器件，其性能的好坏直接影响惯性导航系统的精度。激光陀螺零偏对环境温度的敏感性［2］制约了其精度的进一步提高，因此建立其零偏温度误差模型并进行实时补偿具有重要的工程意义和实用价值［3⁃6］。

激光陀螺温度补偿模型按其适用环境不同可分为静态模型与动态模型。静态模型不考虑温度变化过程中温度变化率的影响，适用于外界环境温度变化较为缓慢的场合。动态温度误差模型考虑温度变化过程中变温率的影响，适用于环境温度变化较快的场合［7］。为了使所建立温度补偿模型在各种环境下均具有良好的补偿效果，这里结合工程实际，针对某型号二频机抖激光陀螺，采用一种将静态温度补偿模型与动态温度补偿模型分开建模再综合考虑的方法，即首先通过恒温实验得到静态温度误差模型，然后设置变温实验对激光陀螺进行测试，对采集的陀螺输出扣除该温度下静态模型输出值后，对扣除后的数据建立动态模型，最后再将两部分模型综合起来的建模方法。

1 激光陀螺温度补偿实验方案设计

1.1 数据采集及处理

实验采用某型号的机抖激光陀螺进行研究，首先在激光陀螺阴极附近放置测温电阻，激光陀螺安装在磁屏蔽盒中，通过金属底板将其固定于温箱的水平台面上。为了消除温度变化对电路的影响，将陀螺电源、数据处理与采集电路都放在温箱外，按1Hz的采样频率采集陀螺输出与测温电阻的温度值。通电启动后，陀螺实际测量值为地球自转角速度在当地水平面的分量ωiesinL。其中，ωie为地球自转角速度，L为当地纬度值。只要保证每次试验陀螺的安装位置固定不变，该值在每次实验中均为常值，因为陀螺的温度误差补偿模型主要是对陀螺的零偏漂移进行补偿，因此该常值的影响可不用考虑。

1.2 实验环境温度设置

实验中为得到静、动态温度误差模型，需分别设置不同的环境温度实验。其中，静态环境温度实验分别在-40℃～60℃。每隔10℃取1个温度点，设置温箱在对应温度点下保温，将陀螺通电启动，待温度稳定后取1h的陀螺脉冲平均值与采样温度平均值，作为该温度下陀螺的输出。动态温度环境试验设置温箱温度环境为25℃-60℃-0℃的温度循环，在60℃、0℃温度点下保温2h，每次实验进行2个温度循环，实验结束后在25℃室温下保温。温箱温度设置如图1所示，在升降温过程分别中设置0．15℃／min、0．5℃／min、1℃／min、3℃／min不同温变速率进行多组实验。

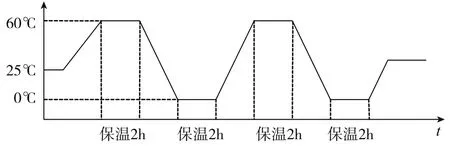
图1　温箱温度环境设置Fig.1 Environment setting of temperature box

2 激光陀螺温度补偿模型的建立

2.1 静态温度补偿模型

静态环境温度实验得到11个不同恒定温度点下的陀螺输出零偏值，静态模型即要根据这些实验数据，建立陀螺静态零偏B0（T）［（°）／h］与传感器测量温度T（℃）之间的关系，可以直接采用式（1）所示的多项式拟合它们之间的关系。其中，k0为模型的常数项，其与温度无关，最终的温度误差模型不包含该常数项，这里为了对比模型补偿效果方便，先将其保留，ki为温度对应阶次的系数，n为多项式模型的阶次。

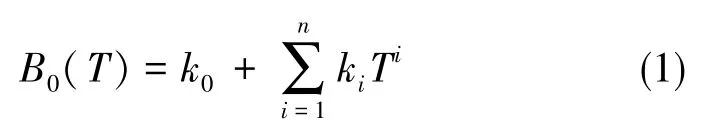
图2所示为实验测得陀螺在恒定温度点下的零偏值，图2中给出了1阶、2阶、3阶模型的拟合效果，可以看出曲线的拟合阶次越高，拟合精度越好，但相应的计算量也越大。综合补偿效果与计算量考虑确定拟合模型为3阶，根据实验数据利用最小二乘法可得静态温度误差模型如式（2）所示。

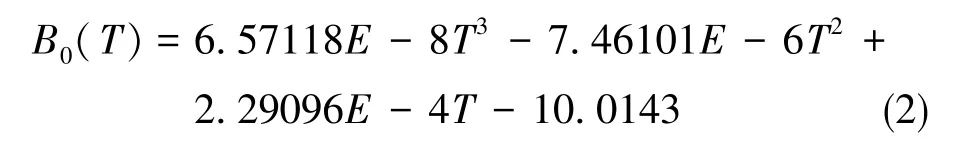
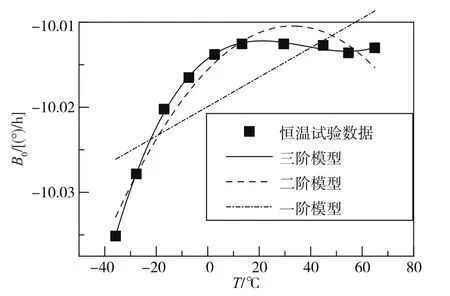
图2　恒温下陀螺输出Fig.2 Gyro output in constant temperature

2.2 动态温度补偿模型

分别在升降温过程中选择0．15℃／min、0．5℃／min、1℃／min、3℃／min四种不同的变温速率，按图1所示的温度循环对陀螺进行动态温度实验。图3所示为4组实验陀螺原始零偏输出B与采样温度T之间的关系。由于实验进行了2个温度循环，因此图3中横坐标每一个温度实际对应着2个升温过程与2个降温过程。从图3中可以看出，在变温率为0．15℃／min、0．5℃／min时，曲线无明显“回滞”，可以认为温度与陀螺零偏之间存在一一对应关系，此时忽略升降温过程中温度变化率的影响，不会造成较大的误差。而在变温率为1℃／min和3℃／min时，实验数据中出现了“回滞”现象，即出现了在升降温过程中，即使在采样温度点相同时陀螺零偏不同的现象，且温变速率越大，这种不一致现象越明显。这表明在环境温度变化较快时，温度不是决定陀螺零偏的唯一要素。此时若忽略升降温过程中变温率的影响将会导致较大的误差，必须考虑温度变化过程中变温速率的影响，需要建立动态温度误差模型来对其进行补偿。

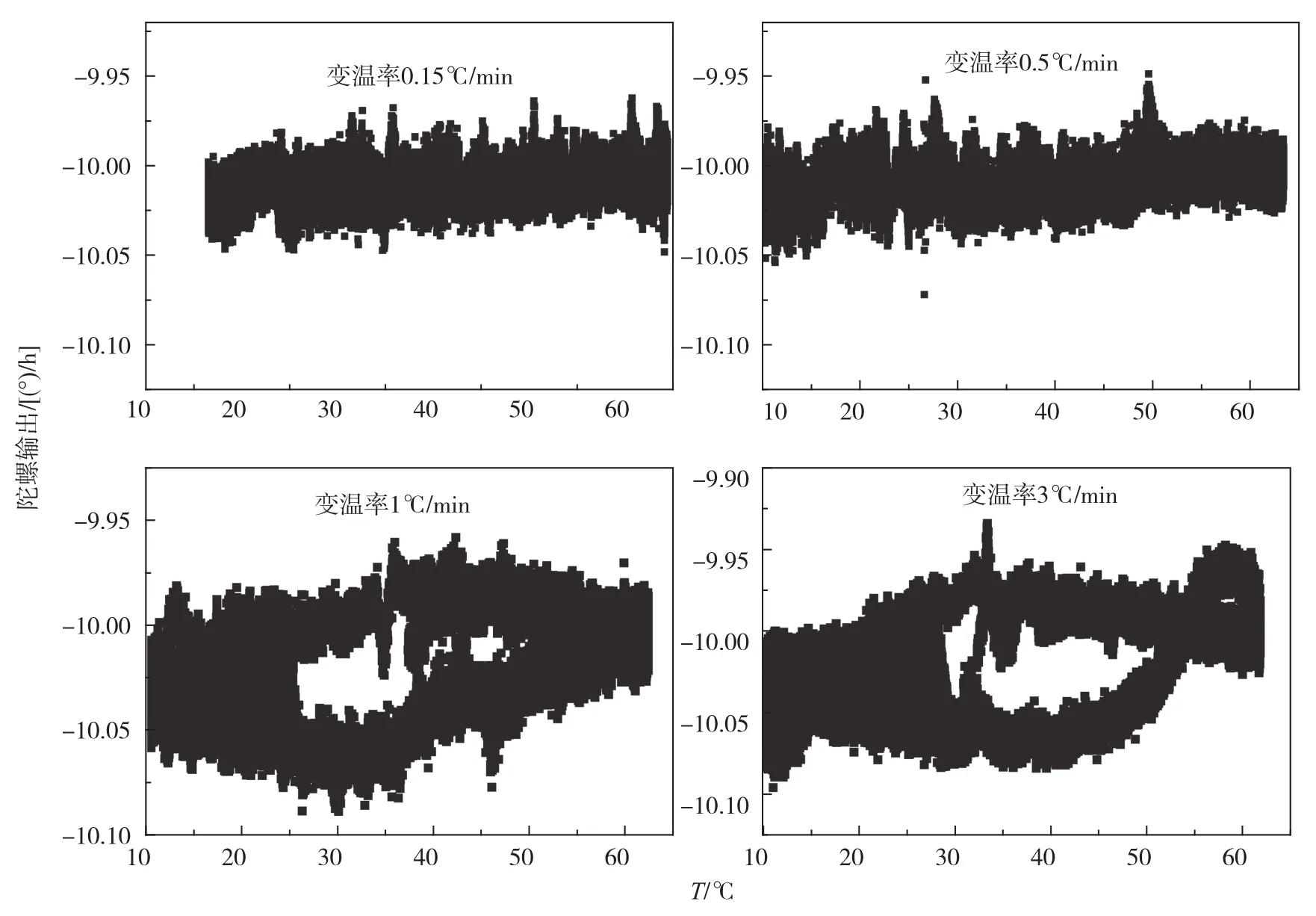
图3　动态温度试验数据Fig.3 Experimental data of dynamic temperature

为了将陀螺动态温度误差模型与静态温度误差模型分开考虑，将实验采集的陀螺原始采B与对应温度点的静态温度误差模型B0（T）求差值得到dB=B-B0（T）。动态模型即考虑用温度变化率dT（由于实验采集频率为1Hz，在这里有补偿dB，建立动态误差模型dB（T，dT），最后再将静、动态模型相加得到最终的综合温度补偿模型Bias（T，dT）=B0（T）+dB（T，dT）。将dB（T，dT）全部用含有dT的因子来进行拟合，这样的好处是当陀螺工作在恒定温度环境下时（dT=0），此时dB（T，dT）=0，Bias（T，dT）=B0（T），即综合补偿模型补偿值即为陀螺在该恒定温度下的零偏均值，可以避免静、动态模型之间相互交叉影响，使温度补偿模型在缓变与快变的温度环境中均适用。

这里取变温率为1℃／min的数据来进行分析，将dB由含dT的因子项dT、dT2、dT3、dT4、TdT、TdT2、TdT3、T2dT、T3dT、T4dT来进行拟合。图4所示为陀螺动态采样序列及各拟合项的序列，这些项是否影响显著还需进行逐步回归分析。逐步回归分析原理是在所考察的全部因素中，按对因变量作用的显著程度的大小，取最显著的变量，逐一引入回归方程，对因变量作用不显著的那些变量自始自终都未被引入；另一方面，已被引入回归方程的变量，在引入新变量后如发现其对因变量的作用变为不显著时，则随时从回归方程中剔除，直至没有新变量能引入方程，且已引入方程的所有变量均不需剔除为止。用Matlab逐步回归分析工具stepwise对数据进行分析之后，可知除dT4、T4dT外，其余项影响都是显著的。对实验数据经过最小二乘拟合可得动态误差模型如式（3）所示。补偿效果如图5所示。其中模型补偿前的精度为0．021414（°）／h，补偿后精度为0．00878（°）／h，模型精度得到了显著的提高。按相同的方法对其他变温率下的实验条件的数据进行建模，得到的动态补偿模型及补偿效果如表1所示。

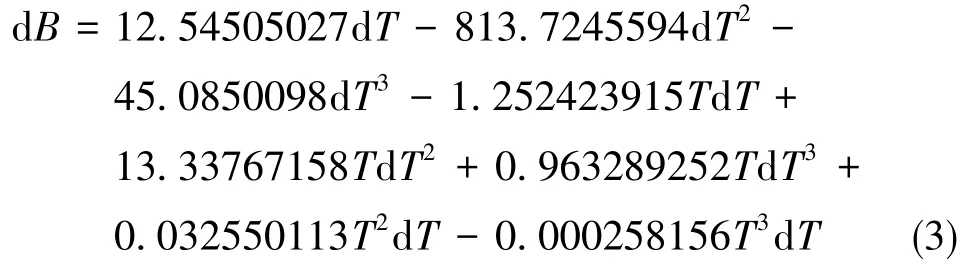
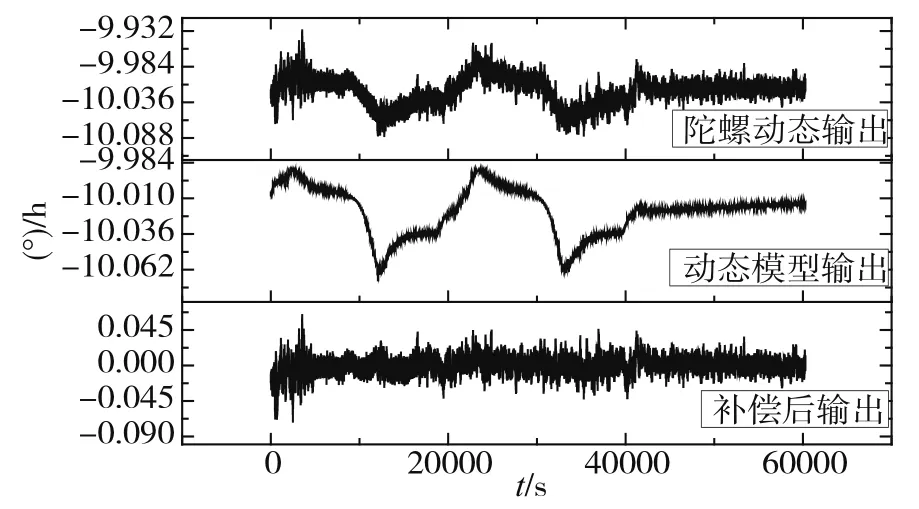
图5　模型补偿效果Fig.5 Model compensation effect

图4　变温率1℃／min时陀螺数据序列Fig.4 Gyro data sequences of 1℃／min temperature rate

表1　各变温率下动态补偿模型Table 1 Dynamic compensation model under each temperature rate

2.3 温度模型环境适应性研究

激光陀螺在实际使用过程中，在通过温度实验辨识出补偿模型的系数后，将得到的系数烧写到程序中，利用温度传感器测得的温度值计算出当前的零偏，将其在陀螺输出中扣除即可进行实时补偿。从表1中可以看出，在不同的变温环境下得到的温度补偿模型系数并不完全一样，为了选取最优的模型，需要验证各模型在不同温度环境下的补偿效果。这里将变温率为0．15℃／min、0．5℃／min、1℃／min、3℃／min得到的温度补偿模型称为模型1、模型2、模型3和模型4。通过温度环境实验分别采集变温率为0．15℃／min、0．5℃／min、1℃／min、3℃／min各3h的陀螺输出，分别用这4个模型对采集的陀螺输出进行补偿，补偿效果如图6所示。从图6中可以看出，模型1、模型2的补偿效果类似，模型3、模型4的补偿效果类似。模型1能够准确补偿变温率为0．15℃／min、0．5℃／min数据段陀螺零偏漂移，对于1℃／min数据段也有一定补偿效果，但没有模型3补偿效果好，对于3℃／min数据段甚至出现了与陀螺零偏变化趋势相反的补偿效果，说明模型1已经不能用于变温率为3℃／min的温度环境。类似地，模型3对变温率为1℃／min、3℃／min具有良好的补偿效果，对0．15℃／min、0．5℃／min补偿效果不好。可知该4个模型均有一定的适应范围，这是由于这些模型系数是在单一变温率的温度环境实验下辨识的，得到的模型只能对与实验温度环境接近的温度环境下使用。为了得到一个使用环境温度范围大的温度模型，这里设计一个包含0．15℃／min、0．5℃／min、1℃／min、、2℃／min、3℃／min变温率的动态温度环境试验，辨识系数后得到式（4）所示的温度补偿模型5，用该模型对各数据段进行补偿，从图6可以看出，模型5在各种环境温度下均有良好的补偿效果。因此将模型5确定为最终的动态模型，最终的综合模型为Bias（T，dT）=B0（T）+dB。

3 模型补偿效果验证

激光陀螺在使用过程中环境温度的变化是不确定的，因此还需对模型进行随机变温试验验证。这里让陀螺在30℃环境温度下通电启动，分别随机以3℃／min、2℃／min、1℃／min、0．5℃／min的不同变温速率进行的温度循环，同时为了验证模型在恒温下补偿效果，实验最后在30℃保温1h。试验采集数据及模型的补偿效果如图7所示，补偿前陀螺漂移为0．019748（°）／h，补偿后为0．007471（°）／h，可知模型对随机变温环境也有很好的补偿效果。

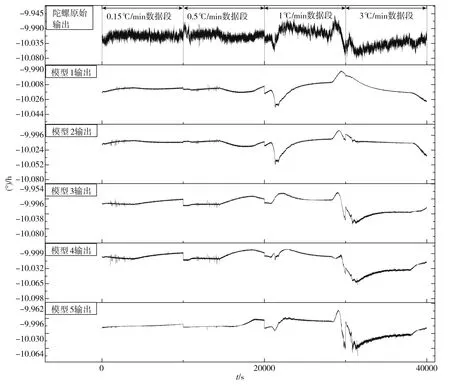
图6　各模型补偿效果验证Fig.6 Compensation effect verification of each model

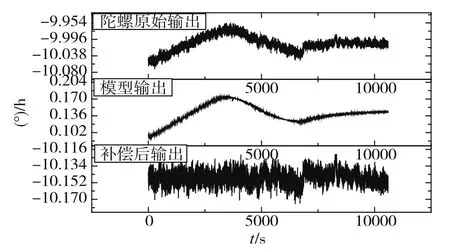
图7　随机变温环境下模型补偿效果验证Fig.7 Model compensation effect verification under randomly variable temperature

温度模型的补偿效果最终还是需要通过实际导航实验进行验证。这里将陀螺温度误差补偿模型烧写到导航软件中，将惯导系统分别在通电自然升温、温箱中快速变温两种工作环境下进行12h静态导航验证。图8～图11为补偿前后导航结果。其中，自然升温条件下12h内的位置精度分别为：补偿前0．892n mile／h，补偿后0．789n mile／h；快速温变条件下位置精度分别为：补偿前5．03n mile／h，补偿后1．04n mile／h。可知所建立的温度模型在慢变和快变的温度环境下均适用，其中环境温度变化越快，补偿效果越明显。

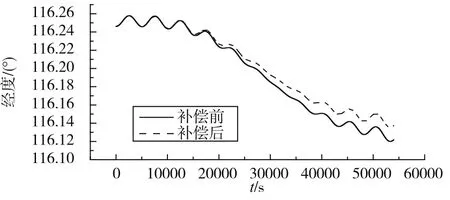
图8　自然升温导航经度对比Fig.8 Navigation longitude under spontaneous elevating temperature

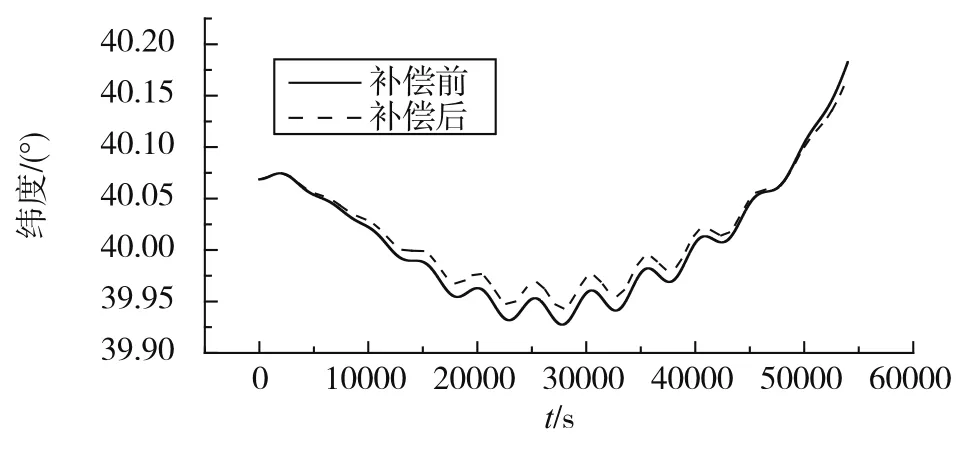
图9　自然升温导航纬度对比Fig.9 Navigation latitude under spontaneous elevating temperature

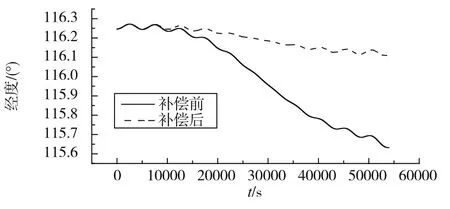
图10　快速变温导航经度对比Fig.10 Navigation longitude under alternating ambient temperature

图11　快速变温导航纬度对比Fig.11 Navigation latitude under alternating ambient temperature

4 结论

文中提出了一种将静态温度误差模型与动态误差模型分开建模的方法，实验验证该方法建立的温度补偿模型在不同环境温度下均具有良好的补偿效果。在大量实验的基础上，得出在缓慢变化温度环境中，陀螺零漂与温度存在一一对应关系，此时忽略变温率的影响不会造成太大误差。在复杂或快速的温变环境中，激光陀螺零偏除与温度值有关外，受温变速率的影响也不可忽略，且环境温度变化越快，温变速率影响越显著。在设计辨识激光陀螺补偿模型系数的温度实验时，要充分考虑到激光陀螺的实际应用工作温度环境以提高模型的补偿效果。

［1］Titterton D，Weston J．Strapdown inertial navigation tech⁃nology［J］．IEEE Aerospace＆Electronics Systems Maga⁃zine，2004，20（7）：33⁃34．

［2］吴国勇，顾启泰，郑辛，等．环形激光陀螺温度模型［J］．清华大学学报（自然科学版），2003，43（2）：180⁃183．WU Guo⁃yong，GU Qi⁃tai，ZHENG Xin，et al．Thermal model of ring laser gyro［J］．Journal of Tsinghua University（Science adn Technology），2003，43（2）：180⁃183．

［3］潘献飞，杨杰，吴美平．复杂温变环境下的激光陀螺零偏补偿方法［J］．中国惯性技术学报，2011，19（2）：234⁃238．PAN Xian⁃fei，YANG Jie，WU Mei⁃ping．RLG bias com⁃pensation method in complex temperature variation environ⁃ment［J］．Journal of Chinese Inertial Technology，2011，19（2）：234⁃238．

［4］赵小宁，李县洛，雷宝权．激光陀螺零偏温度补偿研究［J］．中国惯性技术学报，2004，12（3）：55⁃57．ZHAO Xiao⁃ning，LI Xian⁃luo，LEI Bao⁃quan．Temperature compensation for ring laser gyro［J］．Journal of Chinese Inertial Technology，2004，12（3）：55⁃57．

［5］曹平平，卫育新，师为建，等．激光陀螺组合零偏温度补偿研究［J］．压电与声光，2012，34（4）：533⁃536．CAO Ping⁃ping，WEI Yu⁃xin，SHI Wei⁃jian，et al．Study on temperature compensation for ring laser gyro integrated［J］．Piezoelectrics and Acoustooptics，2012，34（4）：533⁃536．

［6］张鹏飞，王宇，汤建勋，等．机抖激光陀螺多温度点实时温度补偿方法的研究［J］．兵工学报，2010，31（5）：562⁃566．ZHANG Peng⁃fei，WANG Yu，TANG Jian⁃xun，et al．Re⁃search on methods for compensating temperature of me⁃chanically dithered RLG［J］．Acta Armamentarii，2010， 31（5）：562⁃566．

［7］杨慧哲．温度误差对激光陀螺零偏温度补偿精度的影响分析［J］．光学与光电技术，2014，12（2）：98⁃100．YANG Hui⁃zhe．Effect of temperature error on the temper⁃ature compensation accuracy of RLG’s bias［J］．Optics＆Optoelectronic Technology，2014，12（2）：98⁃100．

APPlication Research of One TyPe Laser Gyro TemPerature ComPensation Method

ZHANG Zhen，ZHANG Lin，CHEN Shan⁃qiu，DU Shao⁃jun
（Beijing Aerospace Times Laser Inertial Technology Co．，Ltd．，Beijing 100094）

Temperature is one of main factors resulting in laser gyroscope drift．In the field of high precision strapdown inertial navigation，it is very important to build laser gyroscope temperature compensation model．According to a large amount of experiments，the laser gyroscope drift under different temperature environments was analyzed and a method of building stat⁃ic temperature error model and dynamic temperature error model separately was presented．It is verified that the model can a⁃dapt to slow change temperature environment and rapid change temperature environment by environmental adaptability experi⁃ments．At last，it is shown that the model can be used for engineering application by actual navigation experiments．

laser gyro；temperature compensation；static temperature error model；dynamic temperature model

V241．5+58

A

1674⁃5558（2016）02⁃01219

10．3969／j．issn．1674⁃5558．2016．06．011

2015⁃12⁃24

张震，男，硕士，研究方向为导航、制导与控制。