翼伞系统动力学建模与仿真研究

常冠清，张　泽，仇海涛，范国梁，翁璐斌

（1．北京航天控制仪器研究所，北京100039；2．中国科学院自动化研究所，北京100190）

翼伞系统动力学建模与仿真研究

常冠清1，张泽1，仇海涛1，范国梁2，翁璐斌2

（1．北京航天控制仪器研究所，北京100039；2．中国科学院自动化研究所，北京100190）

以精确空投系统研究为背景，综合运用运动力学和空气动力学知识，建立了翼伞系统6自由度非线性动力学模型，该模型包括3自由度沿系统质心的平动和3自由度绕系统质心的转动。根据此模型分析了翼伞系统的整体运动特性（包括运动轨迹和姿态等），并进行了常值风场对翼伞系统飞行特性的影响研究，得出了翼伞系统在滑翔、转弯和雀降模态下的主要飞行参数，从而为翼伞系统飞行控制系统的设计提供了重要的理论依据。

翼伞系统；动力学建模；风场；飞行仿真

0 引言

随着军民领域对精确空投系统的需求不断提高，翼伞空投系统受到越来越多的关注和研究［1⁃4］。通过设计合理的翼伞系统自主控制系统，可大幅提高空投的精确度。而研究翼伞系统的动力学建模和仿真则是设计相应控制器的必要前提。

国内外对翼伞系统建模也进行了较多的研究，翼伞系统9自由度模型［3］、12自由度模型［4］相继建立并进行了相应的数值仿真。但这些模型较为复杂，非常不利于翼伞系统控制器的优化设计。而本文根据运动力学和空气动力学理论建立的翼伞系统6自由度非线性动力学模型，不仅保证了翼伞系统的主要飞行特性，而且相对较为简单，便于翼伞系统自主控制器的设计。同时，考虑到实际环境中存在风场的影响，本文根据建立的6自由度模型研究了风场对翼伞系统滑翔、转弯、减速和雀降等飞行模态的影响，获得了翼伞系统一些重要的飞行参数，为预测不同环境下系统性能和控制系统参数选择提供了较好的依据。

1 坐标系定义及相互关系

在建立翼伞系统动力学方程之前，首先引入建模过程中需用到的几种坐标系。

1）大地坐标系OIXIYIZI：原点OI取空间某一固定点（通常取伞衣完全展开后，系统质心所在位置），OIZI铅垂向下，OIXIYI与水平面平行，水平轴的方向根据初始条件来选取。

2）物伞体坐标系OBXBYBZB：原点OB位于翼伞系统的质心，OBZB轴过回收物质心，指向回收物一方，OBXBZB为翼伞的几何对称面，OBXB指向伞衣前缘，OBYB轴与其他两坐标轴构成右手系。

3）牵连大地系ODXDYDZD：原点OD位于翼伞系统的质心，其他各轴方向与大地坐标系的相应轴一致。

4）气流坐标系OAXAYAZA：原点OA位于翼伞的质心，OAXA为相对气流的方向，OAZA在翼伞的几何对称面内，指向翼伞的下翼面，OAYA轴与其他两坐标轴构成右手系。

5）翼伞伞面坐标系OPXPYPZP：原点OP处于翼伞伞面的空气动力学中心（可视为翼伞压心），OPXP与翼伞下翼面平行，指向翼伞前缘，OPZP在翼伞的几何对称面内，指向翼伞的下翼面，OPYP轴与其他两坐标轴构成右手系。

物伞体坐标系B与大地坐标系I之间通过3个欧拉角φ、θ、φ进行旋转转换，在3⁃2⁃1旋转次序下，φ即表征横滚角，θ表征俯仰角，φ表征航向角。物伞体坐标系B到大地坐标系I的转换矩阵RIB可表示如下：

物伞体坐标系B到翼伞伞面坐标系P的转换矩阵RPB由翼伞初始安装角μ来确定。RPB可表示为：

其中，矩阵RIB和RPB中均用到了如下缩写：C∗=cos（∗）、S∗=sin（∗）。气流坐标系A和翼伞伞面坐标系P之间通过攻角α、侧滑角β进行旋转转换。翼伞系统各坐标系与角α、β和μ如图1所示。

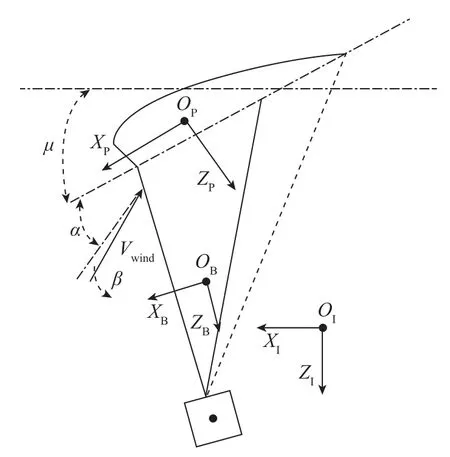
图1　翼伞系统坐标系及相关角度示意图Fig.1 Frames of parafoil system and associated angles

2 翼伞系统动力学建模

2.1 基本假设

为便于问题研究，现对翼伞系统及空间环境作如下假设：

1）翼伞是展向对称的，伞衣完全张满后具有固定的形状（后缘的下偏操纵除外）；

2）翼伞和回收物刚性连接成一整体；

3）伞衣的质心和压心重合，且位于弦向距前缘1／4处；

4）平面大地，重力加速度为常值。

2.2 翼伞系统运动学方程

设PI=［xIyIzI］T为翼伞系统在大地坐标系下的位置矢量，VI=［uIvIwI］T为翼伞系统在大地坐标系下的速度矢量，VB=［uBvBwB］T为翼伞系统在物伞体坐标系B下的速度矢量，Θ=［φ θ φ］T为翼伞系统相对大地坐标系的姿态和航向矢量，WB=［p q r］T为翼伞系统相对物伞体坐

标系的旋转角速度。根据牛顿-欧拉定理可得翼伞系统基本运动学方程如下：

平动三自由度方程：

其中，FW为翼伞系统在物伞体坐标系下的重力，FA为翼伞系统产生的物伞体坐标系下的空气动力，FS为回收物产生的物伞体坐标系下的有效阻力，FAM为翼伞系统附加质量产生的物伞体坐标系下的附加动力为由WB产生的反对称矩阵，其具有如下形式：

转动3自由度方程：

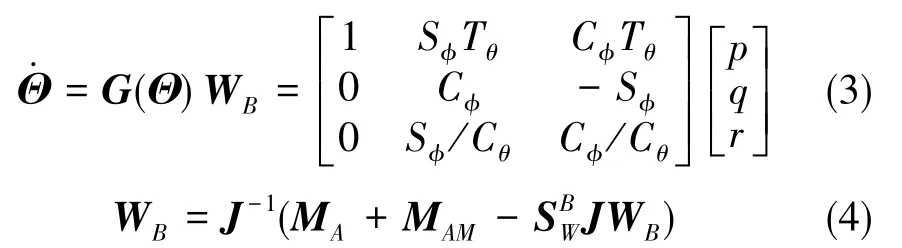
其中，MA为翼伞系统产生的物伞体坐标系B下的空气动力矩，MAM为翼伞系统附加质量产生的物伞体坐标系B下的空气动力矩，J为翼伞系统的转动惯量矩阵，其可表示如下：

2.3 翼伞系统受力和力矩计算

根据牛顿定律，翼伞系统在物伞体坐标系下的重力FW可计算如下：

其中，m为翼伞系统总质量，g为当地重力加速度大小。

翼伞系统产生的物伞体坐标系下的空气动力FA可通过式（6）计算［5］：

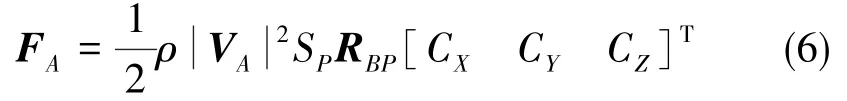
其中，ρ为当地的大气密度，SP为翼伞全展开后的伞衣面积，CX、CY和CZ为翼伞系统空气动力学相关参数，VA=［uAvAwA］T为翼伞系统在翼伞伞面坐标系P下的空速矢量，其可由式（7）表示［6］。式中，VA/I为风速在大地坐标系I下的矢量表示：

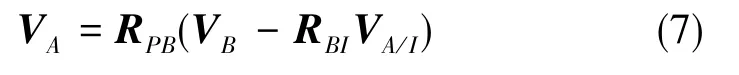
由式（7）可计算翼伞系统的飞行攻角α和侧滑角β为：α=atan（wA/uA），β=asin（vA/|VA|）。

回收物产生的物伞体坐标系B下的有效阻力FS可由式（8）计算得出［6⁃7］：

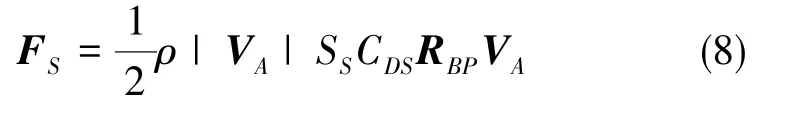
其中，SS为回收物的阻力特征面积，CDS为载荷的阻力系数。

翼伞系统附加质量产生的物伞体坐标系B下的附加动力FAM可由式（9）计算得出［6⁃7］：

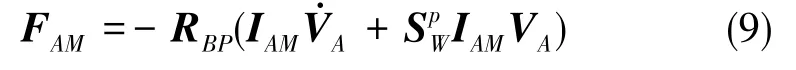
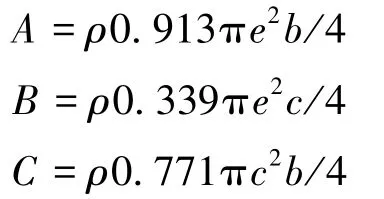
其中，b为翼伞展长，c为翼伞弦长，e为翼伞伞衣厚度，ρ为当地大气密度。

翼伞系统产生的物伞体坐标系B下的空气动力矩MA可由式（10）计算得到［5⁃7］：

其中，b、c分别为翼伞的展长和弦长，Cl、Cm和Cn分别为翼伞的气动力矩系数。

翼伞系统附加质量产生的物伞体坐标系B下的空气动力矩MAM可由式（11）计算得出：

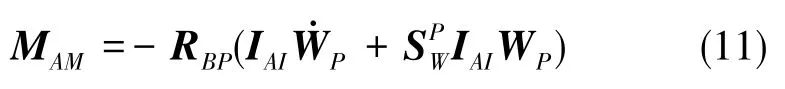
其中，IAI为翼伞系统附加质量产生的惯性矩矩阵，其具有如下形式：IAI=diag（IAIBIC）。其中，IA、IB和IC根据文献［8］可近似计算如下：

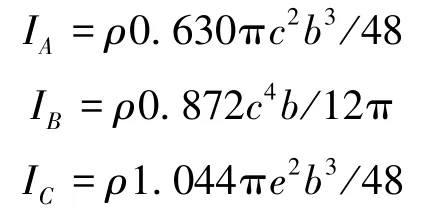
2.4 空气动力学参数建模

根据文献［5］，翼伞系统的相关气动参数可建模如下：

其中，δs为翼伞双侧操纵绳同时下偏量（以占全下偏量的百分比表示），δa为翼伞双侧操纵绳下拉的操纵量之差（以占全下偏量的百分比表示），CLδa、CDδa、CYβ、CYr、CYδa、Clβ、Clp、Clr、Clδa、Cmq、Cmδa、Cnβ、Cnp、Cnr和Cnδa等均为常值参数，而CL（α，δs）、CD（α，δs）和Cmc/4（α，δs）均为α和δs的非线性函数。为便于问题分析，根据文献［9］，CL（α，δs）、CD（α，δs）以及Cmc/4（α，δs）可线性化表示为：

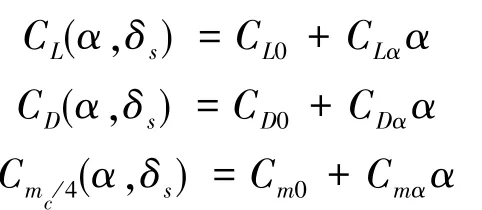
其中，CL0、CLα、CD0、CDα、Cm0和Cmα等均为常值参数。上述气动参数一般通过实验及理论分析的方法获得，本文所述翼伞系统的气动系数的取值可参考文献［10］和文献［11］。

2.5 翼伞系统完备动力学方程

根据式（7）可得VA的导数如下：

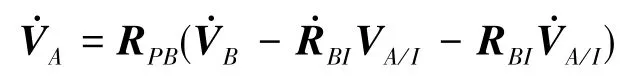
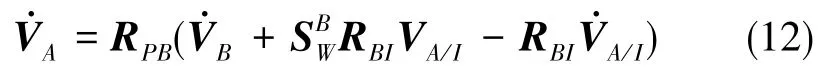
根据式（2）、式（9）和式（12）可得VB的导数如下：

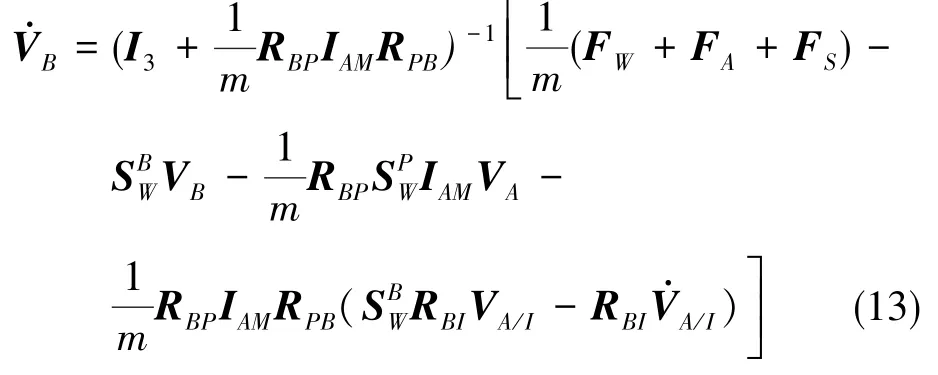
根据WP=RPBWB，式（11）可进一步表示为：

此时，根据式（4）、式（10）和式（14）可得WB的导数如下：

至此，由式（1）、式（3）、式（13）和式（15）就组成了翼伞系统完备6自由度非线性动力学方程，此系统以翼伞下偏量δα、δs和外部风场VA/I为操纵输入。

3 翼伞系统动运动特性仿真与分析

鉴于翼伞系统在飞行过程中，主要有无下偏量时的自由滑翔运动、单侧后缘下偏时的转弯运动及双侧后缘下偏时的减速和雀降运动三种飞行模态。本节将着重考察翼伞系统处于这三种飞行模态时的运动特性，并研究风场对这三种飞行模态的影响。

假设翼伞已完全充满并进入稳定滑翔阶段，且此时大地坐标系和物伞体坐标系重合。翼伞系统的初始状态矢量为：PI=［0 0-2000］Tm、VI=［24 0 8］Tm／s、Θ=［0 0 0］Trad以及WB=［0 0 0］Trad／s。令δα=δs=0，通过配平计算可得翼伞系统初始攻角α=8．4439°。翼伞系统的基本物理参数如表1所示［2］，翼伞系统的相关气动参数可参见文献［7］和文献［10］。

表1　翼伞系统参数表Table 1 Parameters of the parafoil aerial delivery system

3.1 无下偏量时的自由滑翔运动仿真分析

翼伞系统初始处于自由滑翔状态，在t=10s时加入沿大地坐标系+Y方向的水平风场，风速为|VA/I|=6m／s，则翼伞系统运动轨迹及相关运动参数的变化曲线如图2～图5所示。

图2　I系下翼伞系统三轴速度曲线Fig.2 X、Y、Z velocities of parafoil system under I⁃Frame

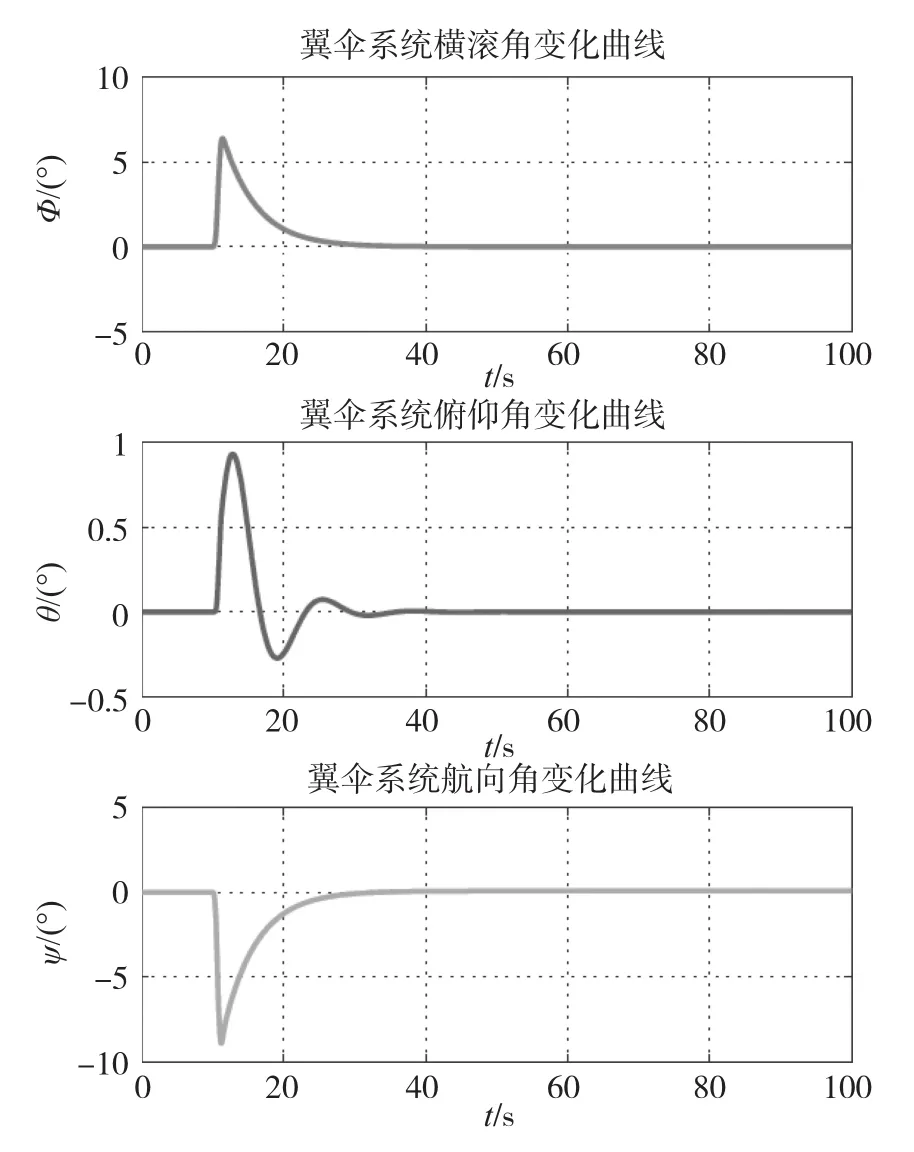
图3　翼伞系统欧拉角变化曲线Fig.3 Euler angles of parafoil system

图4　翼伞系统攻角和侧滑角变化曲线Fig.4 Parafoil attack angle and sideslip angle

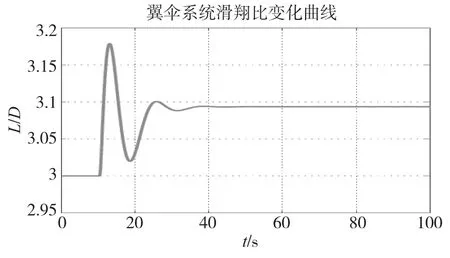
图5　翼伞系统滑翔比变化曲线Fig.5 Parafoil ratio of glide

分析仿真结果，并比较常值侧风作用前后翼伞系统的两个稳定状态，Vx、Vz、θ和φ基本保持不变，Vy则迅速增大并稳定至6m／s。由此表明在不施加控制的状态下，翼伞系统受到侧向风的作用后会沿着风向产生漂移，其漂移速度近似等于侧向风速。翼伞系统侧滑角β则突然增大而后迅速衰减并稳定至0°，衰减时间小于8s，说明β为短周期变化量，且使得翼伞系统稳定的空速矢量作用在纵向对称面内，以维持翼伞伞衣两侧所受气动力的平衡。另外，在常值侧风影响下，翼伞系统滑翔比L/D会产生长周期小幅摆动，经过约20s后稳定在3．09附近，此数值与侧向横风的大小有关。

3.2 单侧下偏时的转弯运动仿真分析

翼伞系统初始处于自由滑翔状态，若在t=10s时加入0．2的右下偏量，同时加入沿大地坐标系+Y向的水平风场，风速为|VA/I|=6m／s，则此时翼伞系统运动轨迹及相关运动参数的变化曲线如图6～图11所示。表2则给出了无风场作用下翼伞系统单侧下偏量与转弯角速度和转弯半径之间的关系。

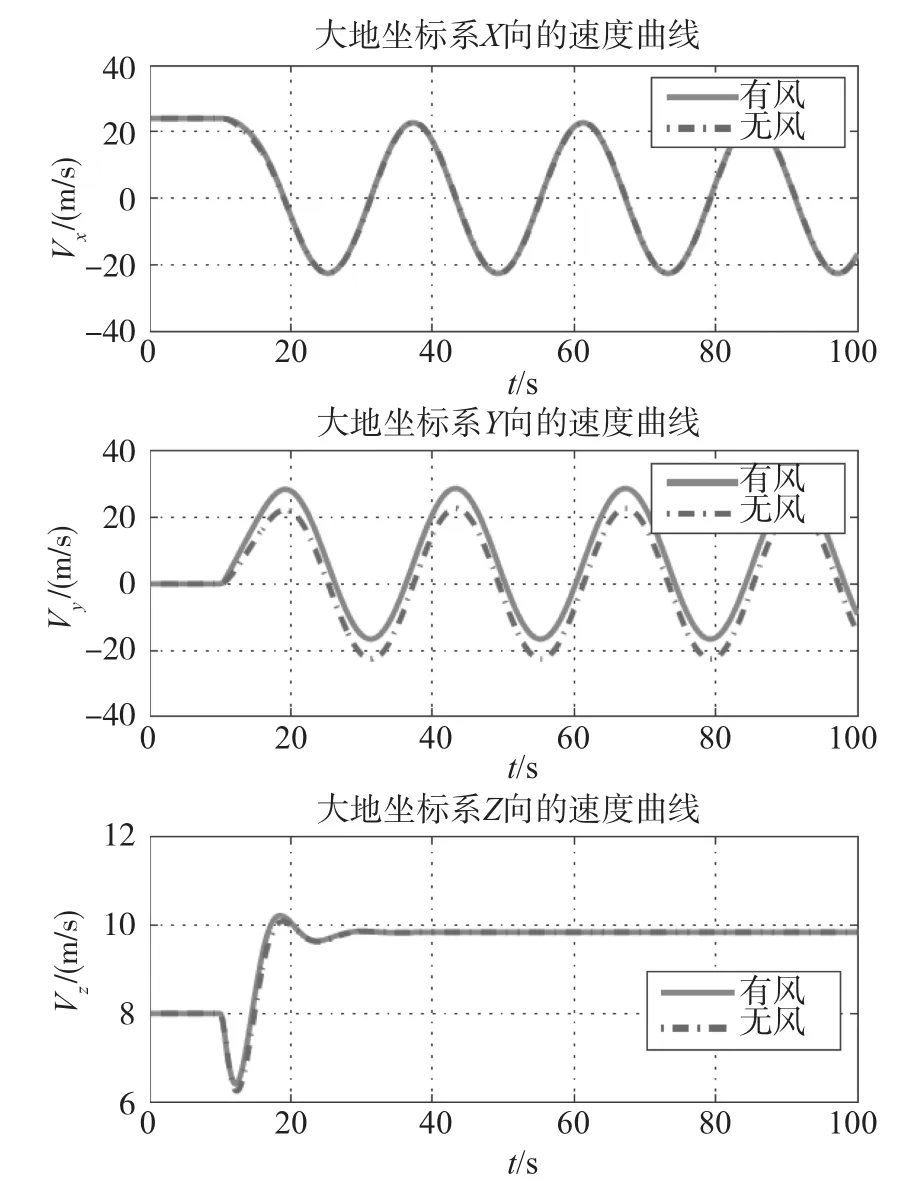
图6　I系下翼伞系统三轴速度曲线Fig.6 X、Y、Z velocities of parafoil system under I⁃Frame

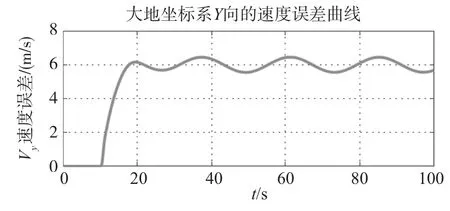
图7　I系下翼伞系统Y向速度误差曲线Fig.7 Parafoil error of Vyunder I⁃Frame

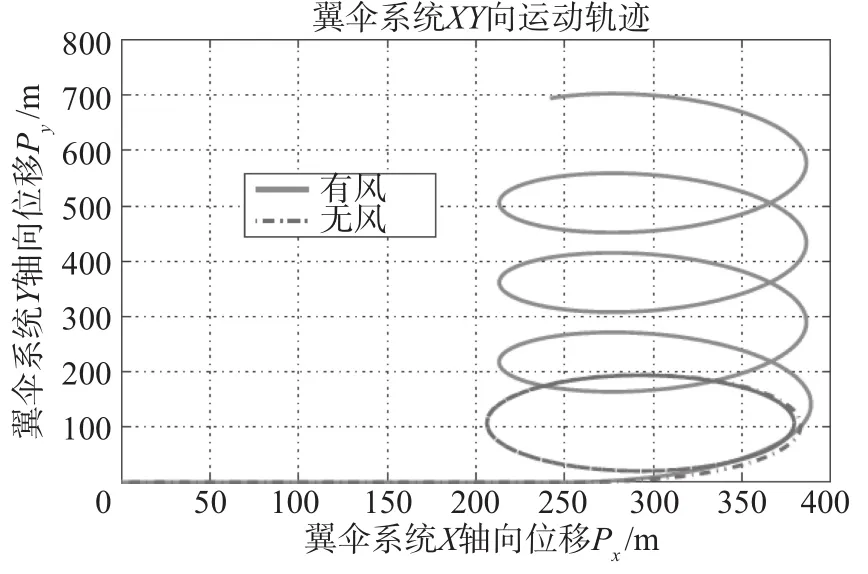
图8　I系下翼伞系统XY向运动轨迹Fig.8 Parafoil trajectory in XY plane under I⁃Frame

图9　翼伞系统欧拉角变化曲线Fig.9 Euler angles of parafoil system

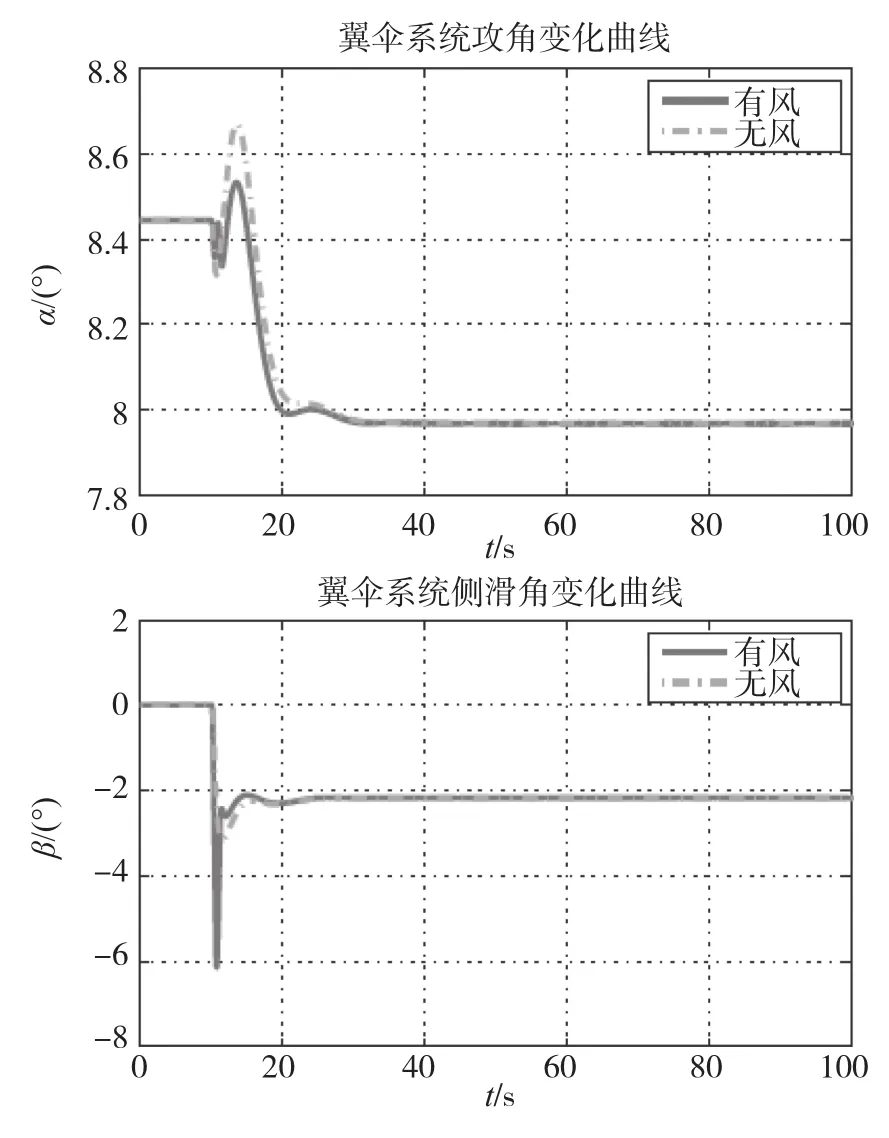
图10　翼伞系统攻角和侧滑角变化曲线Fig.10 Parafoil attack angle and sideslip angle

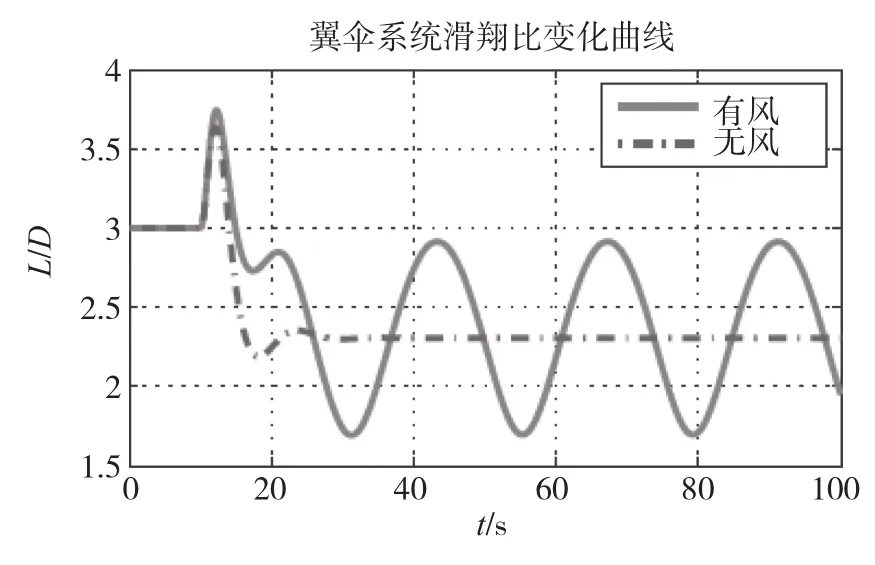
图11　翼伞系统滑翔比变化曲线Fig.11 Parafoil ratio of glide

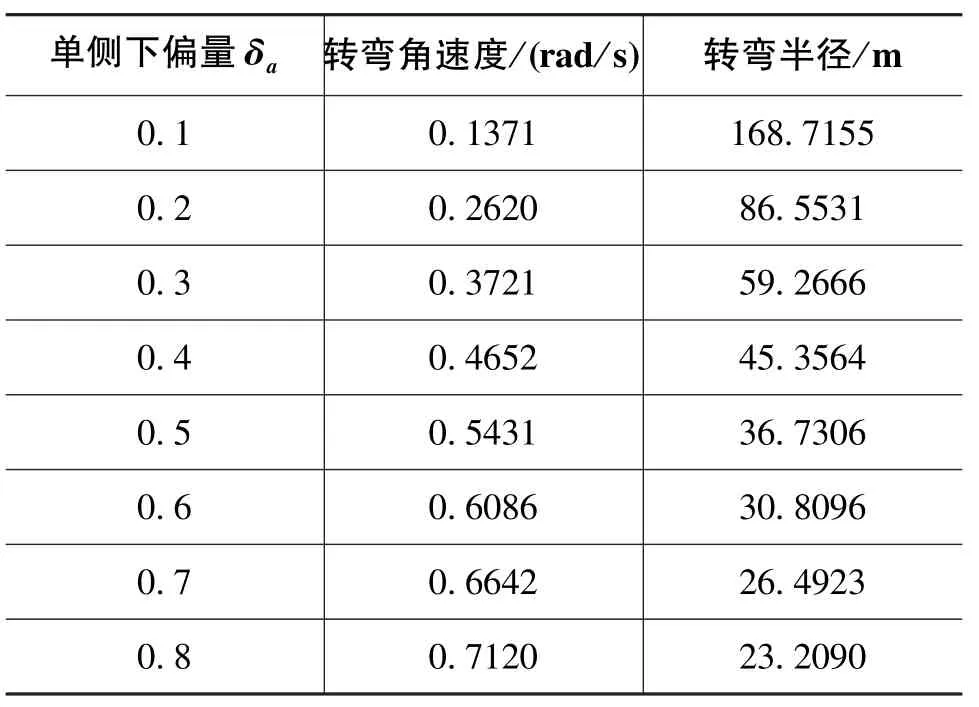
表2　翼伞系统参数表Table 2 Parameters of the parafoil aerial delivery system

分析仿真结果，并比较常值侧风作用前后翼伞系统的两个稳定状态，Vy、Vz基本保持不变，Vy误差则基本稳定在6m／s，说明在单侧下偏时常值侧风亦使得翼伞系统发生等效漂移；翼伞系统横滚角和俯仰角的调整时间约为18s，并分别增大为21．19°和-7．675°，此正好与翼伞系统转弯运动相适应；有无风场情况下，系统攻角α经小幅震荡会稳定于7．67°，滑翔角则会稳定于-2．17°，说明翼伞系统在做转弯运动时，其空速矢量将偏离翼伞系统纵向对称面，以配合翼伞作转弯运动；由表2可知，随着单侧下偏量δa的增大，翼伞系统转弯角速度逐渐增大，在δa＜0．3的情况下，翼伞系统转弯角速度以近似线形的方式递增（斜率约为1．36），这与实际飞行试验相一致。

无风场且翼伞系统在右侧下偏0．2时，翼伞系统各状态量发生上述变化，究其原因主要是当翼伞右侧下偏时，右侧的升力和阻力增大，翼伞系统的瞬时速度减小，同时翼伞系统产生滚转和偏航运动趋势。而通常翼伞系统偏航轴的转动惯量远小于滚转轴的转动惯量，因此翼伞系统易于向右侧发生滚转；由于偏航角速度的影响，使得翼伞伞衣两侧的速度和攻角存在差别，当差别大到一定程度时，会导致伞衣左侧的升力大于右侧的升力，而使翼伞向右侧倾斜，形成了近似协调的倾斜转弯运动。

3.3 双侧下偏时的减速和雀降运动仿真分析

具有双侧后缘下拉操纵量的翼伞系统将做减速或雀降运动，但它们所对应的是不同的运动状态，且控制实施的阶段也不同。减速操纵对应于稳定运动状态，在系统飞行过程中实施，一般用于轨迹修正；而雀降所对应的是动态减速过程，只在最终的着陆阶段实施，其目的是减小人员或回收物触地时的水平和垂直速度，实现无损着陆。

现考察有／无风场时翼伞系统的减速或雀降运动特性。当在t=10s时加入沿大地坐标系X轴反向的横向风，风速为|VA/I|=6m／s，t=40s时同时下拉双侧后缘0．5下偏量，t=80s时同时下拉双侧后缘到满下偏量，翼伞系统运动轨迹变化如图12、图13所示。

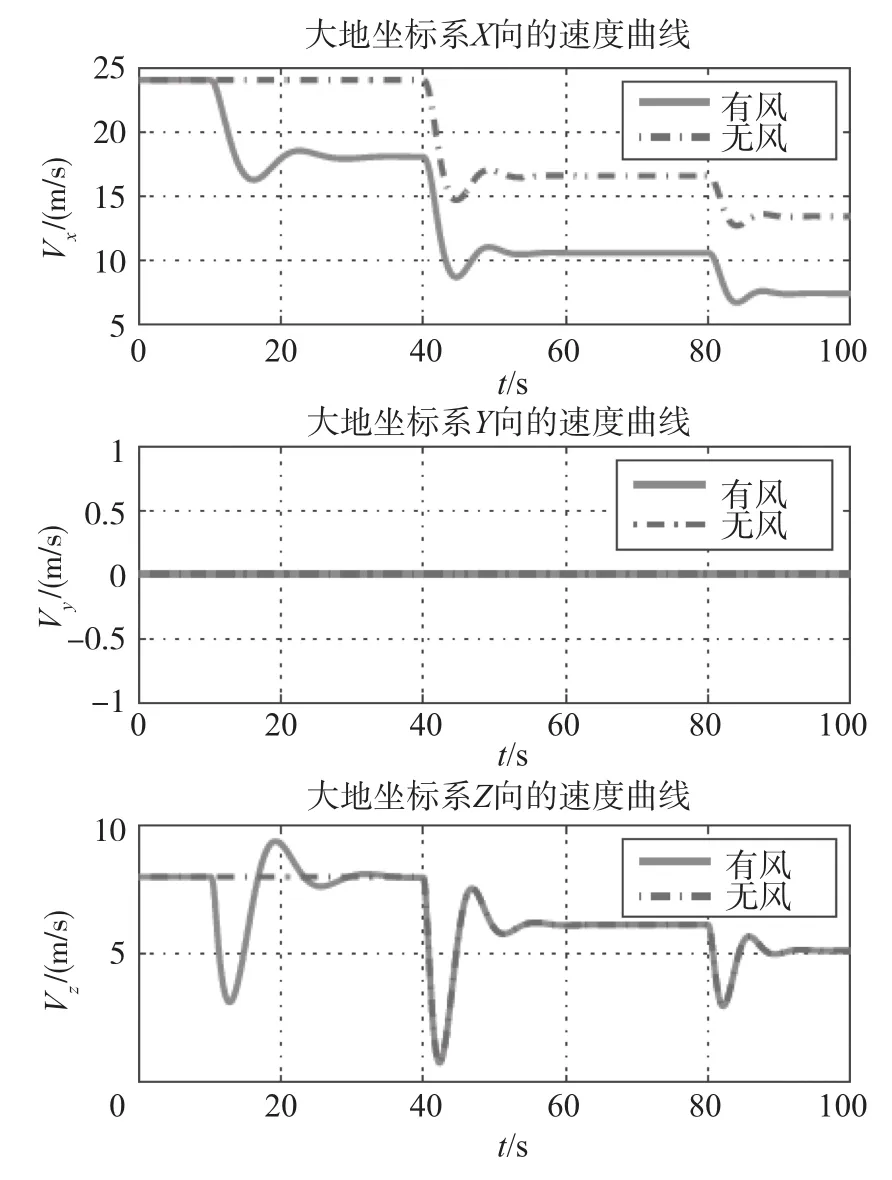
图12　I系下翼伞系统三轴速度曲线Fig.12 X、Y、Z velocities of parafoil system under I⁃Frame

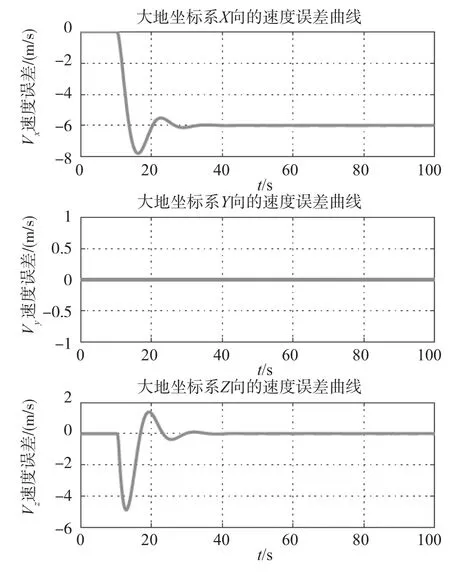
图13　I系下翼伞系统三轴速度误差曲线Fig.13 X、Y、Z velocity errors of parafoil system under I⁃Frame

分析仿真结果可知，无风情况下翼伞双侧下偏0．5或1．0时，翼伞速度Vx、Vz在短时间内均迅速减小，稳定后的速度也比之前小很多，这正好契合减速和雀降的要求［12］。另外，由图12、图13可知，全下偏时Vz最小速度比半下偏时最小速度要大，这主要是由于半下偏时翼伞系统速度较大，翼伞气动外形变化明显，翼伞系统更容易达到失速状态，致使翼伞系统最小速度较小；而全下偏时翼伞系统速度已变得较小，翼伞气动外形变化较半下偏时要小，致使此时翼伞系统最小速度较大。从仿真结果还可以看到，在翼伞系统减速和雀降时，若加入常值侧风，仅使翼伞系统相应轴向的速度减小6m／s，而其他轴向的速度变化较小。

4 结论

本文建立了翼伞系统6自由度非线性动力学模型方程并进行了全面仿真数值分析。通过无下偏、单侧下偏、双侧下偏操纵控制验证了所建模型的正确性，得到了翼伞系统转弯角速率与单侧下偏量的对应关系，获得了翼伞系统许多重要且有益的参数。同时进行了常值风场对翼伞系统滑翔、转弯、减速和雀降飞行状态的影响研究，得出了无论是滑翔、转弯还是雀降状态，翼伞系统稳定后，水平风场对翼伞系统飞行速度的影响可近似为加入风场前速度与风场速度的矢量和。而翼伞系统对外部风场的稳定时间大约为20s，在此时间段内，翼伞系统的航迹要根据控制操纵方式和具体风场情况来分析。

［1］郭舒伟，董阳彪，秦子增．物伞系统动力学模型和讨论［J］．航天返回与遥感，2008，29（3）：38⁃44．GUO Shu⁃wei，DONG Yang⁃biao，QIN Zi⁃zeng．Dynamic model and discussion of the parachute and payload system［J］．Spacecraft Recovery＆Remote Sensing，2008，29（3）：38⁃44．

［2］熊菁．翼伞系统动力学与归航方案研究［D］．国防科技大学，2005．XIONG Jing．Research on the dynamics and homing project of parafoil system［D］．National University of De⁃fense Technology，2005．

［3］Mooij E，Wijnands Q G J，Schat B．9⁃DOF parafoil／pay⁃load simulator development and validation［C］．AIAA ModelingandSimulationTechnologiesConference，Austin，2003．

［4］Vishnyak A．Simulation of the payload⁃parachute⁃wing system flight dynamics［C］．AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar，London，1993．

［5］Prakash O，Ananthkrishnan N．Modeling and simulation of 9⁃DOF parafoil⁃payload system flight dynamics［C］．AIAA Atmospheric Flight Mechanics Conference and Ex⁃hibit，2006．

［6］Slegers N J．Effect of canopy⁃payload relative motion on control of autonomous parafoils［J］．Journal of Guidance，Control，and Dynamics，2010，33（1）：116⁃125．

［7］Slegers N，Beyer E，Costello M．Use of variable incidence angle for glide slope control of autonomous parafoils［J］．Journal of Guidance，Control，and Dyanmics，2008，31（3）：585⁃596．

［8］Lissaman P，Brown G．Apparent mass effects on parafoil dynamics［C］．AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar，London，1993．

［9］谢亚荣．空投任务下翼伞建模与飞行控制研究［D］．南京航空航天大学，2011．

XIE Ya⁃rong．Modeling and flight control research on air⁃drop parafoil［D］．Nanjing University of Aeronautics and Astronautics，2011．

［10］Brown G J．Parafoil steady turn response to control input［C］．12thAIAA Aerodynamic Decelerator Systems Tech⁃nologyConferenceandSeminar，London，1993：248⁃254．

［11］Lingard J S．The performance and design of ram⁃air par⁃achutes［C］．PrecisionAerialDeliverySeminar，Technical Resport，1981．

［12］王利荣．降落伞理论与应用［M］．北京：中国宇航出版社，1997．WANG Li⁃rong．Parachute theory and application［M］．Beijing：China Aerospace Press，1997．

Dynamic Modeling and Simulation of Parafoil Aerial Delivery System

CHANG Guan⁃qing1，ZHANG Ze1，QIU Hai⁃tao1，FAN Guo⁃liang2，WENG Lu⁃bin2
（1．Beijing Institute of Aerospace Control Devices，Beijing 100039；2．Institute of Automation，Chinese Academy of Sciences，Beijing 100190）

Based on the background of the research of precision airdrop system，a 6⁃DOF nonlinear dynamic model of the parafoil system is established，making use of the knowledge of motion dynamics and aerodynamics comprehensively．The model consists of three degrees of freedom system along the centroid of the translation and three degrees of freedom a⁃round the centroid rotation system．According to this model，the overall motion of the parafoil system is analyzed（including translational trajectory and attitude，etc．），and the influence of constant wind field on the flight characteristics of the para⁃chute system is studied．The main flight parameters of the parachute system in the gliding，turning and the bird are ob⁃tained，which provide an important theoretical basis for the flight control system design．

parachute system；dynamic modeling；wind field；flightsimulation

V445．2

A

1674⁃5558（2016）01⁃01178

10．3969／j．issn．1674⁃5558．2016．06．006

2015⁃08⁃10

国家自然科学基金（编号：60904006，61005067）；中国科学院科技创新基金（编号：CXJJ⁃11_M10）。

常冠清，男，工程师，研究方向为飞行器自动控制。