基于惯性辅助的GPS相对定位算法

彭旭飞，陆志东，岳亚洲，高关根

（1．西安飞行自动控制研究所，西安710065；2．飞行器控制一体化技术国防重点实验室，西安710065）

基于惯性辅助的GPS相对定位算法

彭旭飞1，2，陆志东1，2，岳亚洲1，2，高关根1，2

（1．西安飞行自动控制研究所，西安710065；2．飞行器控制一体化技术国防重点实验室，西安710065）

针对GPS信号易受干扰遮挡以及利用载波相位差分进行相对定位时整周模糊度浮点解精度差、搜索空间大的不足，提出INS辅助的GPS相对定位算法。首先采用INS／GPS深组合方式，实现伪距、伪距率的滤波平滑；然后利用校正后的惯性信息、伪距、载波相位集中滤波得到高精度的浮点解和协方差阵；最后利用LAMBDA算法得到模糊度固定解和相对位置信息。文中使用GPS实测数据和仿真惯导数据进行相对定位试验，结果表明在GPS信号受到短时遮挡时，有惯性辅助和没有惯性辅助相比，东北天3个方向的平均误差分别下降66．45％、82．32％、85．66％；且该算法可改善模糊度指标，压缩整周模糊度搜索空间，提升整周模糊度求解效率。

惯性辅助；载波相位差分；相对定位；整周模糊度

0 引言

使用GPS的双差载波相位差分可以实现厘米级甚至是毫米级的相对定位精度，快速可靠的整周模糊度求解是其工程应用的关键［1］。

但是卫星信号易受干扰遮挡且刷新率低，会导致完好性与连续性的不足。另外，由于卫星接收机受大气层延时、多径误差、接收机噪声等影响，使得初始模糊度浮点解精度不高。因而限制了其在对定位精度、实时性要求较高的领域（如空中加油、舰载机着舰等）的应用［2］。

惯性导航系统（INS）自主性强，与GPS优势互补，将两者组合起来可以高效发挥2个系统各自的优势。文献［3］～文献［5］对INS辅助整周模糊度求解算法进行研究，但对INS辅助对于模糊度浮点解精度的影响和INS保持相对位置没有过多论述。本文在此基础上，采用深组合分布式滤波器实现INS辅助GPS相对定位。不仅提高卫星导航抗干扰能力［6］，而且利用INS短时精度高的特点，可有效提高模糊度浮点解精度，压缩模糊度搜索空间，提升模糊度解算效率，并能够在卫星失锁的情况下，提供短时的精度保持能力［7］。

1 系统方案

如图1所示，系统由2套INS、GPS接收机、分处理器和1个主处理器组成。分处理器用于单点定位：当卫星信号质量较好时，使用伪距、伪距率进行INS／GPS深组合滤波，并将导航信息输入到主处理器中；当卫星信号质量较差时，采用INS保持其精度。主处理器用于相对定位：当卫星信号质量较好时，使用惯性信息、伪距双差、载波相位双差求解出整周模糊度浮点解及其协方差阵，并使用LAMBDA算法得到固定解和相对位置信息［8⁃9］；当信号质量较差时，采用INS保持其相对位置信息。

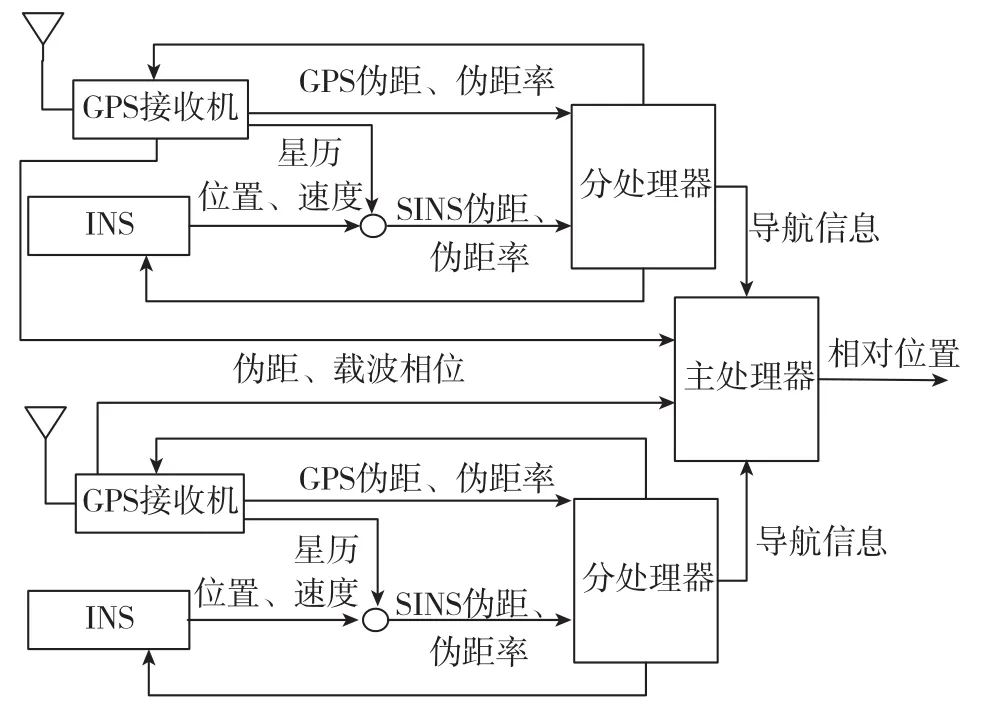
图1　INS辅助GPS相对定位系统方案图Fig.1 System diagram of GPS relative positioning with INS aiding

2 算法设计

2.1 分处理器算法设计

分处理器根据卫星信号质量的好坏决定进行INS／GPS深组合Kalman滤波还是使用INS保持其精度输出。INS／GPS深组合Kalman滤波器算法如下［10］：

（1）状态方程

综合滤波器由两部分组成：一部分是INS的误差状态，另一部分是GPS的误差状态。INS的状态方程可写为：

式中，

其中，φE、φN、φU是平台角误差，δvE、δvN、δvU是速度误差，δL、δλ、δh为位置误差，εbx、εby、εbz为陀螺随机常值漂移误差，εrx、εry、εrz为陀螺一阶马尔科夫过程，为加速度计误差。

对于捷联惯导系统，有：

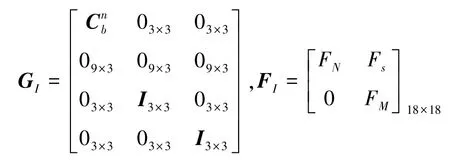
GPS的误差状态方程可写为：

式中，

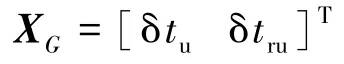
其中，δtu、δtru分别是等效时钟误差相应的距离和等效时钟频率误差相应的距离。

综合以上几式，则得用伪距、伪距率组合的系统状态方程：

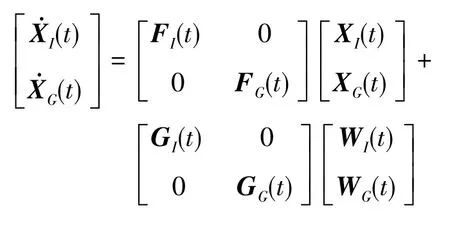
即，

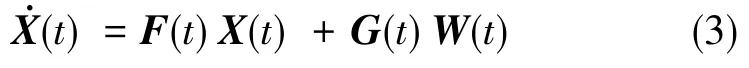
（2）量测方程

系统的量测方程由伪距差量测方程和伪距率差量测方程组成。

伪距差量测方程为：

式中，

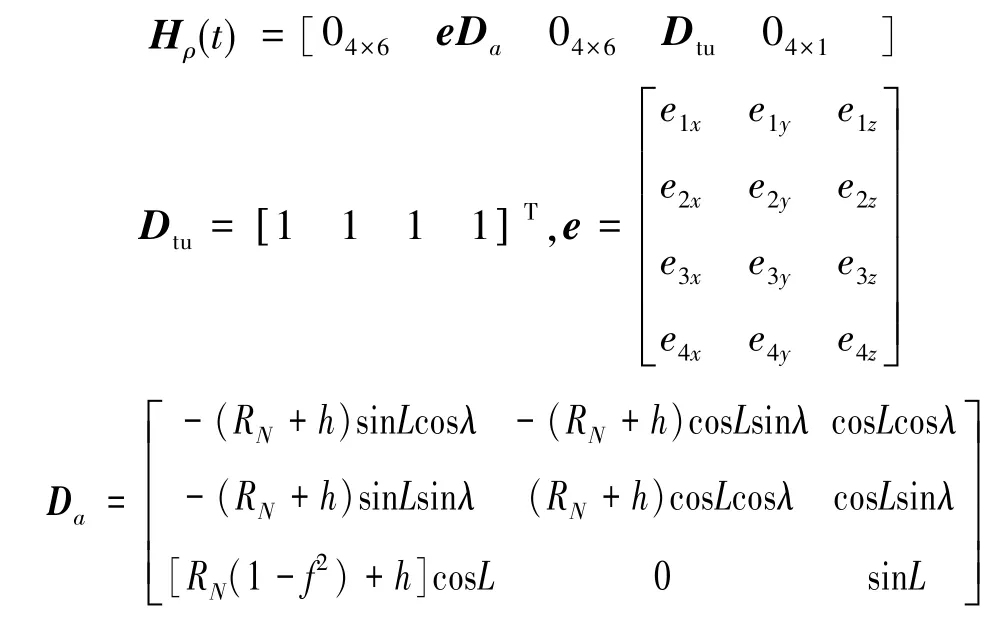
伪距率差的量测方程为：

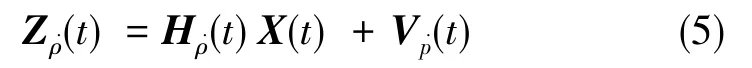
其中，

E是一个4×3的矩阵，设：

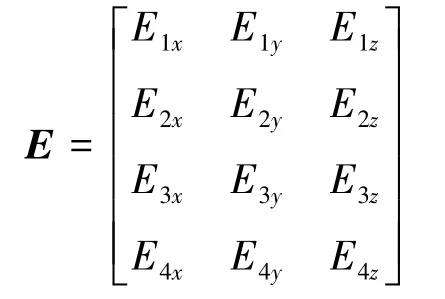
综合以上几式，可得组合导航系统的量测方程为：

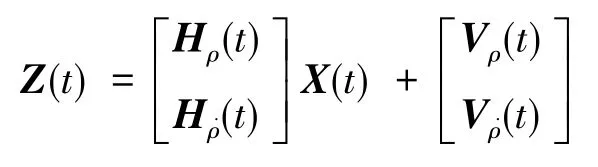
即，

2.2 主处理器算法设计

主处理器用于输出相对位置信息，当卫星信号质量较好时，采用INS伪距单差、GPS伪距双差、GPS载波相位双差进行Kalman滤波得到整周模糊度浮点解及其协方差阵，随后使用LAMBDA算法得到整周模糊度固定解和相对位置信息；当卫星信号质量较差时，LAMBDA算法无法求得整周模糊度固定解，因此用INS保持高精度的定位结果。

（1）状态方程

如图2所示，卫星的位置分别为（xi，yi，zi）、（xj，yj，zj），基准站的位置为（xr，yr，zr），移动站的准确位置和估计位置分别为（xu，yu，zu）和（xu_a，yu_a，zu_a）。移动站准确位置与估计位置的偏差为：

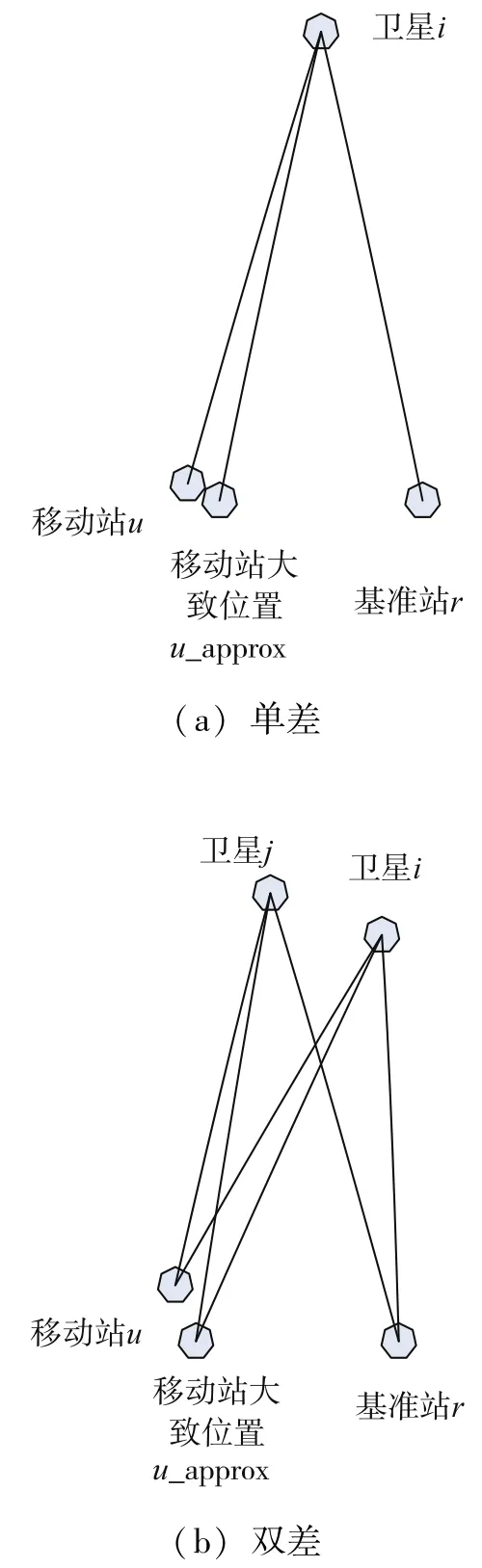
图2　单差、双差示意图Fig.2 Diagram of single⁃difference and double⁃difference

取状态变量：

（2）量测方程

如图2所示，卫星i到基准站r的距离为：

卫星i到移动站u_approx的距离为：

卫星i到移动站u的距离为：

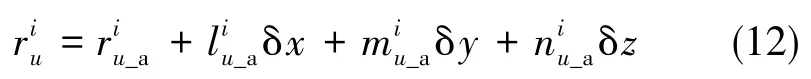
式中，

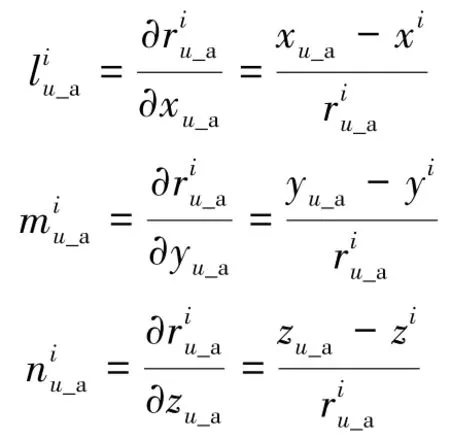
基准站r和移动站u处惯导的位置输出对卫星i做单差为：

基准站r处、移动站u处的伪距测量值分别为：

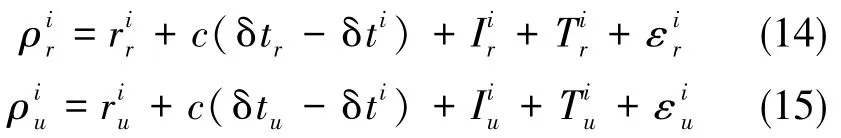
为了消除误差，基准站和移动站对卫星i、j做双差可得：

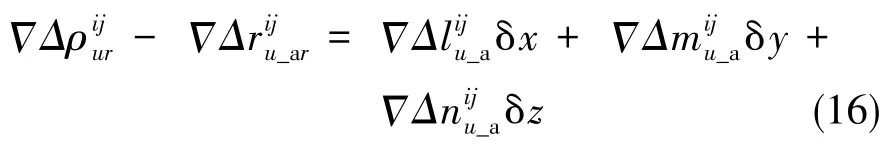
同理，可得载波相位双差测量值为：

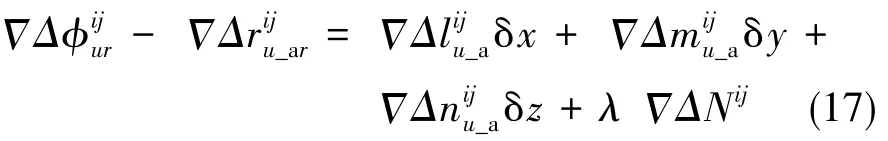
其中，λ为载波波长，Δ ΔN为双差整周模糊度。

联立式（13）、式（16）和式（17）可得：

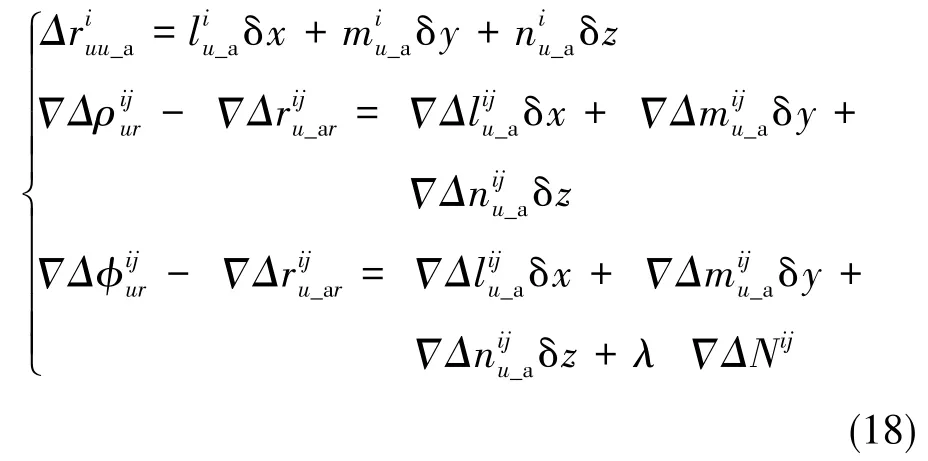
因此，滤波器的观测方程可写为：

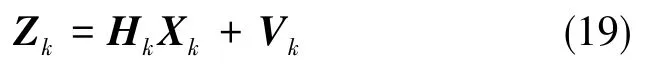
其中，

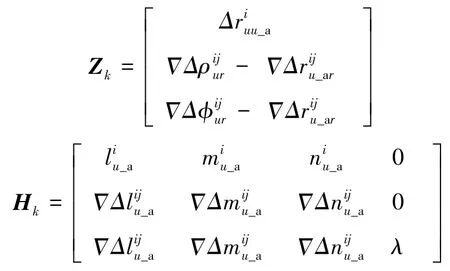
利用惯性辅助得到状态初值X0和估计均方误差初值P0，根据k时刻的量测Zk，就可递推计算得到k时刻的状态估计Xk。其中的整周模糊度浮点解向量可用LAMBDA算法解出其固定解，进而得到相对位置信息。

3 惯性辅助的作用分析

当INS所给的位置精度高于差分码伪距的定位精度时，惯性辅助可起到明显的效果，其作用主要体现在两个方面：一方面在卫星信号受到干扰遮挡，无法得到整周模糊度固定解的情况下，利用INS保持高精度的相对位置输出；另一方面，在卫星信号质量较好的情况下，通过引入更多的高精度观测信息，减小多径误差、接收机噪声等的影响，提高模糊度浮点解的精度和可靠性，压缩模糊度搜索空间，提高搜索效率。具体分析如下：

滤波器的观测方程为：

采用加权最小二乘估计，权值的选取与测量值的精度有关，可用观测值的协方差阵进行表示：

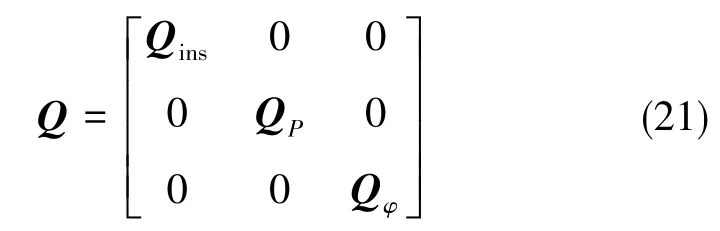
其中，Qins是组合系统计算伪距单差观测值的协方差阵，QP是双差载波伪距观测值的协方差阵，Qφ是双差载波相位观测值的协方差阵。

利用加权最小二乘原理可得：

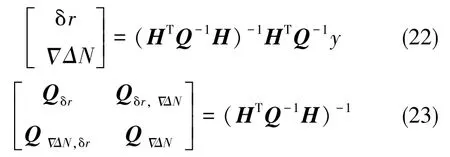
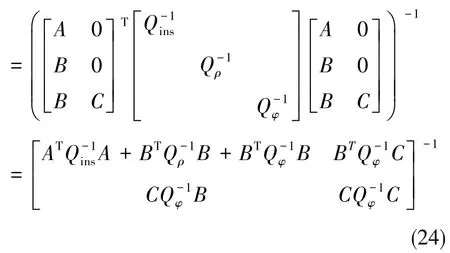
所以，

因此，

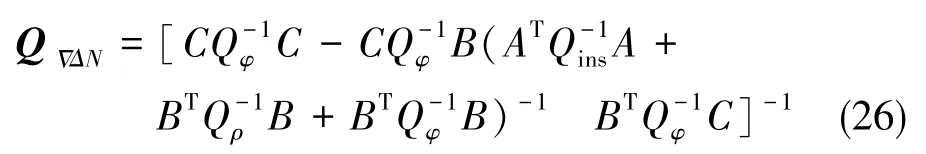
当没有加入惯性信息时，

通过综合比较式（26）和式（27），可容易得到：

通过式（28）可以看出，加入惯性辅助后可减小浮点解的协方差阵，提升浮点解的精度并压缩搜索空间。

为了对模糊度浮点解精度和搜索空间进行直观认识，引入一个评价指标：模糊度衰减因子（ADOP）。

模糊度衰减因子（ADOP）是表征模糊度精度及可靠性的重要指标。其定义如下［11⁃12］：

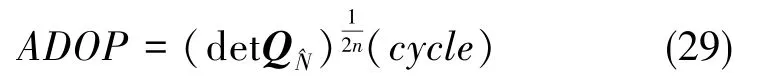
式中，Q^N是模糊度浮点解的协方差阵表示其行列式，n为模糊度的个数，ADOP的单位为周。

同时，定义一个与椭球空间包含的候选数相关联的容积（单位为“周”）［11］：

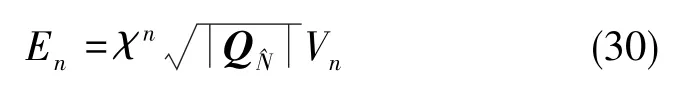
4 实验验证

为验证INS辅助对GPS相对定位精度的影响，本文采用Novatel GPS接收机实测数据和0．8 nm／h（50％CEP）的仿真惯性数据进行半物理仿真验证。并在200s～263s人为遮挡天线，使卫星数减少，卫星质量下降。

如图3所示，是INS／GPS深组合滤波器与INS的位置误差对比图。从图3中可知，INS在500s已经发散到300m，而使用INS／GPS深组合可有效抑制INS的发散，达到较高的定位精度。

图3　INS／GPS深组合位置误差Fig.3 Position error of INS／GPS deep coupled

图4是分处理器的位置误差图。其中，200s～263s由于卫星天线受到遮挡，卫星导航产生2m～3m的定位误差。虽然INS误差随着时间积累而增大，但是在短时间内仍然能保持较高的精度输出。

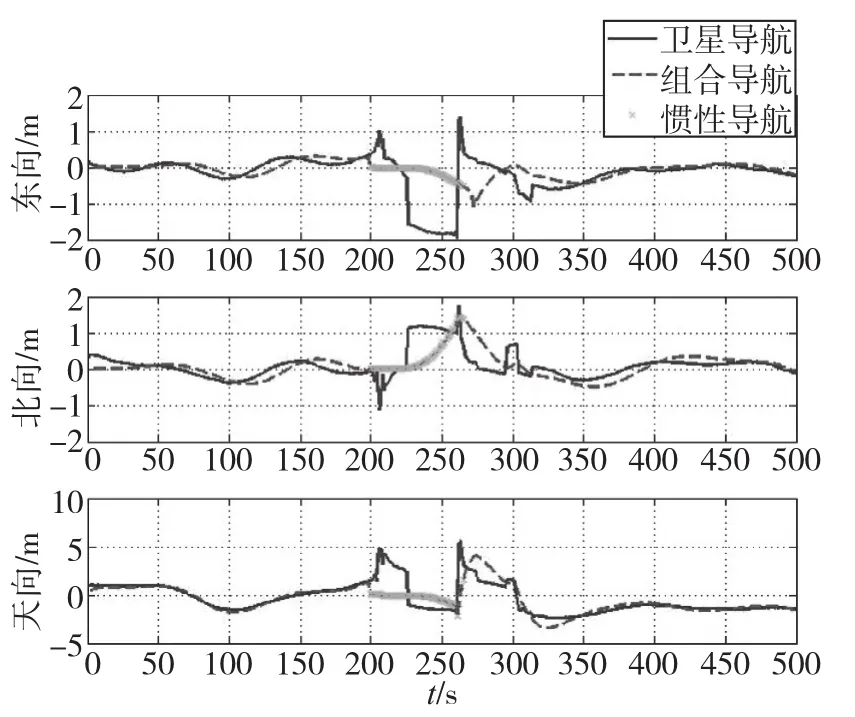
图4　单点定位位置误差Fig.4 Position error of single⁃point positioning

图5是主处理器相对定位的误差图。其中，在200s～263s由于卫星天线受到遮挡，无法解出整周模糊度固定解，相对定位结果产生较大的误差。这时切换至INS，在短时间内提供较高的精度输出。

图5　相对定位位置误差Fig.5 Position error of relative positioning

图6是从5图截取的一段，此时卫星信号质量较好，使用INS伪距单差、GPS伪距双差、GPS载波相位双差解出整周模糊度浮点解，并利用LAMBDA算法得到固定解和相对位置。从图6中可知，东北天3个方向均可达到毫米级的定位精度。

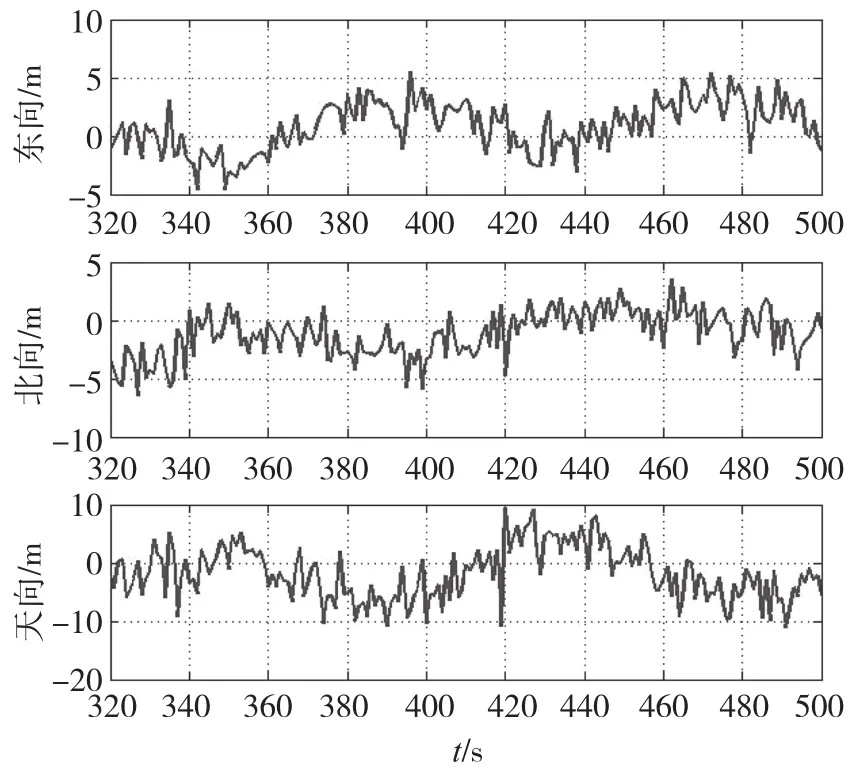
图6　相对定位位置误差Fig.6 Position error of relative positioning

从表1可知，当卫星信号没有遮挡时，东北天3个方向的平均误差在毫米级的范围内。当对卫星信号信息遮挡后，定位精度的平均误差和标准差都增大。对比其中有无惯性辅助可知，加入惯性辅助信息后，可使东北天的平均误差下降66．45％、82．32％、85．66％，说明INS辅助对提高GPS相对定位精度起到了重要作用。

表1　定位精度误差统计表Table 1 Statistics of positioning accuracy error

计算有无惯性辅助情况下的模糊度衰减因子（ADOP）、搜索空间、候选模糊度组合数，结果分别如图7～图9所示。由于在信号质量不好时，在无辅助情况下已无法求解整周模糊度，因此对模糊度解算评价仅针对其中信号质量较好的情况。

从图7～图9的计算结果可以看出，即使在卫星信号较好的情况下加入惯性辅助，仍可有效降低模糊度衰减因子和搜索空间，减小候选模糊度组合数，提升模糊度搜索效率。

图7　模糊度衰减因子Fig.7 ADOP

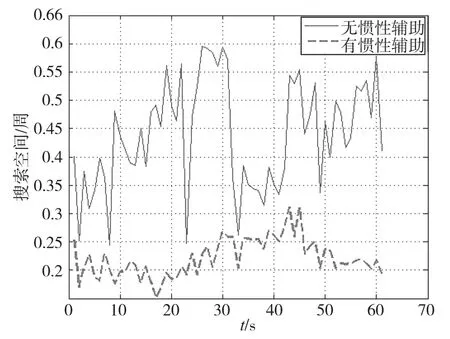
图8　模糊度搜索空间Fig.8 Ambiguity searching space

图9　候选模糊度组合数Fig.9 Number of ambiguity candidates

5 结论

本文利用INS与GPS信息构成深组合滤波器，然后利用组合结果计算伪距单差，利用卫星数据构造GPS伪距、载波相位双差，经过Kalman滤波得到模糊度浮点解和协方差阵，随后使用LAMBDA算法得到整周模糊度固定解和相对位置信息。文中分析了惯性辅助对于保持高精度定位结果和提高模糊度浮点解精度的作用。为验证算法的有效性，用GPS实测数据和INS仿真数据完成了实验室半物理仿真验证，结合模糊度搜索的评价准则，评估有无辅助情况下的算法性能，结果表明当卫星信号受到遮挡中断时，惯性辅助信息可以保持较高精度的相对定位结果；当卫星信号较好时，惯性辅助信息也可以提高模糊度浮点解精度、压缩模糊度搜索空间，从而提升整周模糊度求解的效率。

［1］谢钢．GPS原理与接收机设计［M］．北京：电子工业出版社，2009．XIE Gang．GPS principle and the design of receiver［M］．Beijing：Electronics Industry Press，2009．

［2］Khanafseh S M．GPS navigation algorithms for autonomous airborne refueling of unmanned air vehicles［J］．Dissertations＆Theses Gradworks，2008，44（5）：1670⁃1682．

［3］谢宏飞，郝金明．INS辅助GPS整周模糊度解算方法研究［C］．第四届中国卫星导航学术年会论文集⁃S9组合导航与导航新方法，2013．XIE Hong⁃fei，HAO Jin⁃ming．Research on methods of GPS integer ambiguity resolution with INS aiding［C］．4thChinese Satellite Navigation Academic Annual Meeting⁃S9 New Method of Navigation and Integrated Navigation，2013．

［4］岳淼．GPS载波相位高精度惯性组合导航系统研究［D］．南京航空航天大学，2007．YUE Miao．Research on high precision integrated GPS／INS navigation system based on carrier phase［D］．Nanjing University of Aeronautics and Astronautics，2007．

［5］张晓安，何晓峰，王荔斌，等．惯性信息辅助的载波相位模糊度求解算法［J］．计算机工程与设计，2010，31（13）：3081⁃3087．ZHANG Xiao⁃an，HE Xiao⁃feng，WANG Li⁃bing，et al．Inertial aided algorithm for carrier phase ambiguity resolu⁃tion［J］．Computer Engineering and Design，2010，31（13）：3081⁃3087．

［6］袁俊刚．GPS／惯性紧组合导航系统研究［D］．南京航空航天大学，2011．YUAN Jun⁃gang．Research on GPS／INS tight integrated navigation system［D］．Nanjing University of Aeronautics and Astronautics，2011．

［7］何晓峰．北斗／微惯导组合导航方法研究［D］．国防科学技术大学，2009．HE Xiao⁃feng．Algorithms for BD／MIMU integrated navi⁃gation systems［D］．National University of Defense Tech⁃nology，2009．

［8］Teunissen P J G．A new method for fast carrier phase am⁃biguity estimation［C］．Proceedings of IEEE PLANS’94 Las Vegas，1994：562⁃573．

［9］Teunissen P J G，Jonge P J D，Tiberius C C J M．The least⁃squares ambiguity decorrelation adjustment：its per⁃formance on short GPS baselines and short observation spans［J］．Journal of Geodesy，1997，71（10）：589⁃602．

［10］王惠南．GPS导航原理与应用［M］．北京：科学出版社，2003．WANGHui⁃nan．GPSnavigationprincipleand application［M］．Beijing：Science Press，2003．

［11］Wu H．On⁃the⁃fly GPS ambiguity resolution with inertial aiding［D］．University of Calgary，2003．

［12］Euler H，Landu H．Fast GPS ambiguity resolution on⁃the⁃fly for real⁃time application［C］．Proceeding of 6thIn⁃ternational Geodetic Symposium on Satellite Positioning，Columbus，Ohio，1992：650⁃659．

GPS Relative Positioning Algorithm Based on INS Aiding

PENG Xu⁃fei1，2，LU Zhi⁃dong1，2，YUE Ya⁃zhou1，2，GAO Guan⁃gen1，2
（1．Flight Automatic Control Research Institute，Xi'an 710065；2．National Key Laboratory on Flight Vehicle Control Integrated Technology，Xi'an 710065）

In view that GPS signal is easily been interfered and blocked，as well as many drawbacks when carrier phase differential relative positioning，such as poor accuracy of float ambiguities and large⁃searching space．In this paper，a GPS relative positioning method based on INS aiding is proposed．First of all，INS information，pseudo range and pseudo range rate are achieved filtering smoothing by the use of a deep⁃coupled integrated method．Then，the integrated INS infor⁃mation，pseudo range and carrier phase are used to aid carrier phase to get high precision float ambiguities and their vari⁃ance⁃covariance matrix．Finally，LAMBDA algorithm is used to obtain the integer ambiguities and relative position informa⁃tion．An experiment is conducted with the test data and the inertial navigation data from simulation．The results show that，during GPS signal short outage，the average error in East／North／Up with INS aiding decrease 66．45％，82．32％，85．66％respectively compared to without INS aiding．What's more，this algorithm can improve the ambiguity performance，reduce the ambiguity searching space and increase the searching efficiency．

INS aiding；carrier phase differential；relative positioning；integer ambiguity

V249．328

A

1674⁃5558（2016）01⁃01226

10．3969／j．issn．1674⁃5558．2016．06．002

2016⁃01⁃06

彭旭飞，男，硕士，导航、制导与控制专业，研究方向为卫星导航与组合导航。