SA-PSO算法在智能组卷中的应用研究

盛 魁，马 健，董 辉

(亳州职业技术学院信息工程系，安徽亳州 236800)



SA-PSO算法在智能组卷中的应用研究

盛 魁，马 健，董 辉

(亳州职业技术学院信息工程系，安徽亳州 236800)

通用、健壮、高效的组卷算法是实现考试智能化、规范化、科学化的重要保障。本文在分析智能组卷数学模型及各种组卷算法的基础上，针对目前组卷算法存在组卷时间长、组卷效率低等缺陷，提出了一种基于模拟退火粒子群优化算法(SA-PSO)。将其应用于智能组卷实验，并与RANDOM和PSO算法作比较。实验结果表明，SA-PSO算法使得组卷效率、组卷成功率和组卷满足度等方面均有显著的提高，并且保证了组卷的质量。

模拟退火法；粒子群；智能组卷

“互联网+”教育开启了教育新模式，推动了教育信息化和智能化的快速发展，智能化考试系统因其客观、便捷、准确、安全等特点在各种考试中应用。而在智能化考试系统设计中，组卷算法是保证组卷质量的关键技术，对整个考试系统起着决定性作用。因此，快捷、高效、科学的组卷算法日益成为教育领域和人工智能领域共同关注的热点问题[1]。

智能组卷是按照课程标准和课程教学大纲的要求，运用人工智能技术，由计算机来设计试卷内容，并使生成试卷内容符合设定的各项指标。目前广泛被采用的组卷算法有随机抽取组卷算法、回溯试探组卷算法、遗传算法和定性映射法四类[2]。其中，随机抽取法[3]逻辑结构较简单，易于实现单道试题的快速抽取，但存在很大的不确定性和随意性，无法满足题库多变的要求，不具有智能性。回溯试探法[4]在状态类型和试卷总题量少的试题库系统中组卷效果比较理想，但程序结构较复杂，选取试题随机性差，重题率高，组卷时间长。遗传算法[5]解决了抽题的随机性问题，满足智能组卷系统对于大型试题库与复杂结构组卷的要求，但自动出题的收敛速度比较慢且算法操作比较复杂。定性映射方法[6]能够合理分配不同难度的试题，提高了组卷的效率和成功率，但其结构程序较复杂，数学基础要求较高，实现起来难度大。

本文在分析组卷数学模型、模拟退火算法和粒子群算法的基础上，将模拟退火算法的降温思想和Metropolis准则引入粒子群算法中,提出了一种基于模拟退火和粒子群算法的优化算法(SA-PSO)，用该算法处理智能组卷问题，并通过实例进行验证。

1 智能组卷问题的数学模型

1.1 约束条件

在智能组卷时需要考虑试卷的约束条件，常见的主要约束有试卷总分、试卷总时间、试卷难度、题型分布、知识点分布等。假设一份试卷所包含的试题数为m，每道试题题型有n个约束条件，一份试卷可用一个m×n的矩阵来表示：

(1)

其中，矩阵S中aij表示第i道题的第j个属性，ai1为第i道试题的编号，即试题的唯一标识；ai2为第i道试题的分数；ai3为第i道试题的难度值；ai4为第i道试题对应的知识点编号；ai5为第i道试题对应的认知分类；ai6为第i道试题题型；ai7为第i道试题对应的答题时间；ai8为第i道试题的区分度。目标矩阵满足的约束条件如下：

除上述约束条件外，还可以指定试卷的期望值、使用频度和使用信度等约束条件，在实际组卷过程中,约束条件过多会增加组卷的难度，影响组卷的成功率。

1.2 目标函数

组卷的目标就是从试题库中搜索到满足各项约束分布的试题集，智能组卷本质上是一种多目标寻优问题[7]。本文采用权重系数法对智能组卷建模，组卷问题的目标函数为：

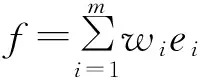
(2)

其中，i为第i个约束的权重；ei为第i约束因素对组卷目标的误差，且目标函数越小越好。

2 模拟退火粒子群优化算法

2.1 粒子群优化算法

粒子群算法(Particle Swarm Optimization，PSO)是一种在模拟鸟类捕食行为的基础上发展起来的启发式全局优化技术[8-9]。设在D维空间中，有N个粒子，粒子i的位置Xi=(xi1,xi2，…,xiD)；粒子i速度Vi=(vi1,vi2，…,viD)；粒子i的局部极值向量为pbest=(pi1,pi2，…,piD)；群种的全局极值向量为pbest=(pg1,pg2，…,pgD)。粒子的速度和位置依据如下方程变化，

(3)

(4)

2.2 模拟退火算法(SA)

模拟退火算法(Simulated Annealing，SA)，其基本思想就是用一个物理系统的退火过程来模拟优化问题的寻优过程，是一种解决组合优化问题的有效近似算法[10-11]，适合于大规模组合优化问题求解。接受最优解的概率可由Metropolis准则来确定，

(5)

其中，T表示控制参数，xi表示当前解，xj表示新产生的解，f(x)表示问题目标函数。

2.3 模拟退火粒子群算法(SA-PSO)

模拟退火粒子群算法(SA-PSO)，是PSO算法中每个粒子在更新速度和位置的过程中引入SA思想而形成的一种新的优化算法。SA-PSO算法先利用PSO的快速搜索能力得到一个较优的群体，然后利用SA的突跳能力实现全局寻优。SA-PSO算法优化实现步骤如下：

Step1 初始化参数：学习因子c1，c2,惯性权重，退火起始温度T和终止后温度T0，迭代次数k，退火速度a。搜索空间的下限Xmin和上限Xmax，粒子运动时速度的最小值Vmin与最大值Vmax；

3 实验结果与分析

3.1 组卷要求和参数设置

为了验证SA-PSO算法的可行性和有效性，以及确定部分算法参数对算法的影响，以数据结构课程为例，进行组卷实验分析。试题库题型表中题量分布为：291道选择题、238道填空题、241道算法分析题、281道算法设计题。模拟退火中退火起始温度T=8000，终止温度T0=0.03，退火速度α=0.9。最大迭代次数为10000，群体粒子数为50。组卷过程中的要求如下：总分为100，估计用时为120分钟，试题难度为0.4900；试卷区分度为0.4050。用户设置参数的各种分布如表1至表3所示，根据AHP方法[12]计算智能组卷各目标权重，结果如表4所示。

表1 题型——分数分布

表2 知识点——分数分布

表3 认知层次——分数分布

表4 试卷的各种约束权重

3.2 组卷效率比较

为了检验SA-PSO算法组卷效果，在实验环境相同的情况下，将随机抽取法(RANDOM)和粒子群算法(PSO)作对比，组卷花费时间如图1所示。可以看出，RANDOM算法的组卷速度较慢，PSO算法的速度也相对较慢，而SA-PSO算法进行全局搜索和局部寻优的平衡搜索，不断趋于最优解，收敛速度快，提高了组卷效率。

图1 组卷效率对比图

3.3 组卷成功率比较

表5表示3种算法组卷成功率的对比结果。SA-PSO算法组卷的成功率高于RANDOM和PSO算法，这说明运用SA-PSO算法进行组卷不但成功率高，而且速度快，具有较好的实用性，为智能组卷提供了一种新的方法。

表5 组卷成功率对比表

3.4 组卷满足度平均值比较

不同组卷算法满足度平均值对比结果如表6所示。运用SA-PSO算法进行组卷试卷难度满足度、区分度满足度和知识点满足度的平均值均高于RANDOM和PSO组卷的满足度平均值。这说明SA-PSO算法是一种有效、实用、科学的组卷算法。

表6 组卷满足度平均值对比表

4 结语

智能考试是教育信息化的一种重要体现，而组卷算法是提高组卷效率、组卷成功率的基本保障。本文将模拟退火思想融入粒子化算法，提出一种基于SA-PSO优化算法。SA-PSO算法不但能以较大的概率挑出局部极值点而且收敛速度快，实现了SA算法和POS算法的优势互补。针对智能组卷的具体应用表明，SA-PSO算法在组卷时不但提高了组卷的效率和成功率，而且满足了组卷的要求，具有很强的实用性，使得生成试卷更加科学、规范。

[1]梁海丽.基于通用试题库的智能组卷系统的开发与实现[D].石家庄:河北科技大学,2011.

[2]夏爱月.基于遗传算法的自动组卷系统研究与实现[J].电脑编程技巧与维护,2009(2):94-95.

[3]张振国,杨柯.新型组卷策略的研究与实现[J].计算机工程与设计,2008(20):5348-5353.

[4]龚完全.基于最小回溯代价的智能组卷算法[D].长沙:湖南大学,2005.

[5]周艳聪,刘艳柳.遗传模拟退火智能组卷策略研究[J].计算机工程与设计,2011(3):1066-1069.

[6]邵红青,冯嘉礼,甘棠仪,等.一种基于定性映射的自动组卷算法[J].计算机辅助工程,2005(2):26-29.

[7]李欣然,樊永生.改进量子行为粒子群算法智能组卷策略研究[J].计算机科学,2013(4):263-239.

[8]Parsopoulos K E,Vrahatis M N.Recent approach to global optimization problem through particle swarm optimization[J].Natural Computing,2002(2):235-256.

[9]Kennedy J,Eberhart R C.Particle swarm optimization[C].IEEE Intrmationa1Conference on Neural Networks Perth,Australia,1995.

[10]王梦兰.智能优化算法的比较与改进[J].中国水运,2012(12):48-49.

[11]刁鸣,邹丽.模拟退火遗传禁忌搜索的多用户检测算法[J].哈尔滨工程大学学报,2014(3):373-377.

[12]张志强,徐斌,何勇灵,等.基于AHP评价方法的发动机性能评价[J].兵工学报,2008(5):625-628.

Research on Application of SA-PSO Algorithm in Intelligent Test Paper

SHENG Kui,MA Jian,DONG Hui

(Department of Information Engineering,Bozhou Vocational and Technical College,Bozhou Anhui 236800,China)

The general,robust and efficient test paper generation algorithm is an important guarantee for the intelligent,standardized and scientific test.In the analysis of intelligent composing mathematical model and algorithm of generating test paper based,according to the generating set of algorithms exist long time of the test paper,test paper efficiency and low defects,puts forward a method based on simulated annealing particle swarm optimization algorithm (SA-PSO).Its application in intelligent test paper composition experiment,and random and PSO algorithm as the comparison experiment results show that,SA-PSO algorithm in efficiency of composing,the success rate of test and the test paper meet degree are increased significantly,and to ensure the quality of the test paper.

simulated annealing;particle swarm;intelligent test paper

2016-03-28

2015年安徽省高等学校省级自然科学研究重点基金项目“物联网技术在中药材种植环境信息采集中的研究与应用”(KJ2015A417)；2015年安徽省高校振兴计划优秀青年人才支持计划(gxyqZD2016529)；2015年安徽省科技攻关计划项目“基于OTO模式的中药材诚信平台研究”(1501zc03031)。

盛 魁(1981- )，男，副教授，硕士，从事农业物联网、数据挖掘和电子商务研究。

TP311

A

2095-7602(2016)10-0042-05