基于维纳滤波的图像还原研究

孙英慧，孙英娟

(1.吉林师范大学计算机科学学院，吉林四平 136000；2.长春师范大学计算机科学与技术学院，吉林长春 130032)



基于维纳滤波的图像还原研究

孙英慧1，孙英娟2

(1.吉林师范大学计算机科学学院，吉林四平 136000；2.长春师范大学计算机科学与技术学院，吉林长春 130032)

本文主要介绍了维纳滤波的原理，并使用Matlab环境进行了实验仿真。实验结果表明，基于维纳滤波的图像复原点扩散函数的选择对还原效果有很大的影响，可以用图像的自相关函数和噪声的自相关函数来提高图像的还原质量。

自相关函数；维纳滤波；图像还原；点扩散函数

图像还原在艺术品的修复、影视作品中的特技以及虚拟现实等领域有着广泛的应用。通常人们进行图像还原采用的方法主要有基于图像润饰技术方法，其中包括基于统计的方法、基于偏微方程的方法和基于环绕的方法，其次是基于纹理合成的技术方法，其中包括纹理映射方法和纹理合成方法等。

1 图像退化模型

在实际生活中，人们捕获的图像其退化原因很难确定，因而对于模糊的已退化的图像，我们很难有效地获取其退化的相关先验知识，因而要对退化进行估计或建模并非易事。经过多年的研究，人们提出了典型的退化模型：图像f(x,y)通过一系统H，然后与某个外部噪声n(x,y)叠加，得到的便是我们获取的退化图像g(x,y)，如图1所示。

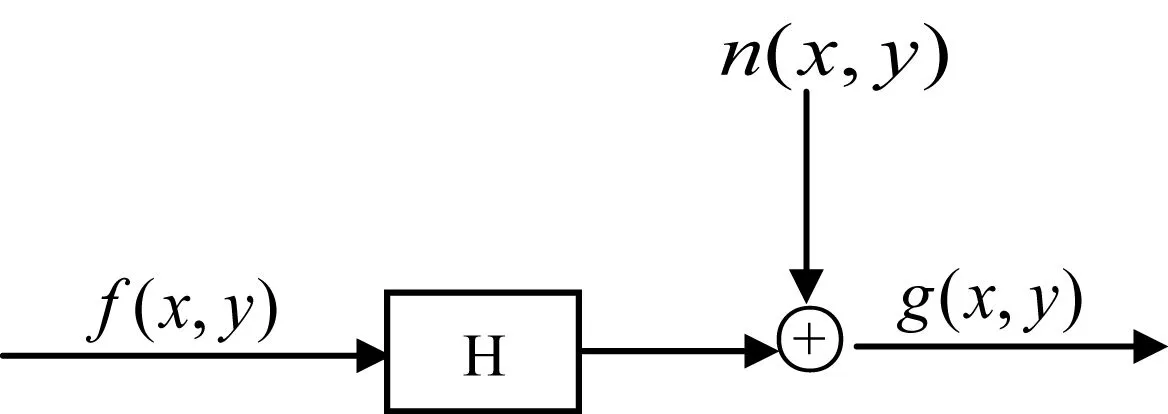
图1 图像的退化模型

人们提出的这个退化图像形成模型是一个预估计过程，根据给出的退化图像g(x,y)进行系统参数估计，便可以近似的恢复出原图像f(x,y)。图像复原的基础在于对系统H的了解，常见的系统有线性和非线性两类。一般地，我们建模时采用的是线性时不变系统。根据系统的特性可以推导出系统的输入信号和输出信号的某些联系，从数学角度出发，可以采用算子或函数h(x,y)来进行描述。于是，图像退化的数学表达式可以表示为

g(x,y)=H[f(x,y)]+n(x,y).

(1)

H[·]可理解为综合所有退化因素的函数或算子。若H为线性时不变系统，有

g(x,y)=f(x,y)*h(x,y)+n(x,y).

(2)

图2 图像的退化与复原过程

2 逆滤波复原法

逆滤波复原法的基本原理：图像退化可能与噪声无关，此时设g(x,y)为退化图像，f(x,y)为原始图像，则退化模型可表示为公式(3)。

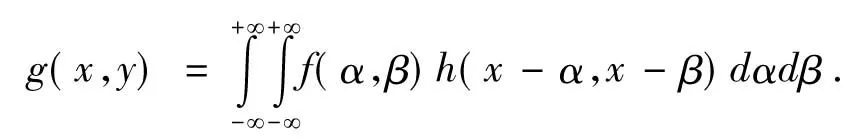
(3)

在此情况下，不妨设退化图像g(x,y)、点扩散函数h(x,y)和原始图像f(x,y)的傅立叶变换分别为G(u,v),H(u,v),F(u,v)，则

G(u,v)=F(u,v)·H(u,v).

(4)

由(4)式有

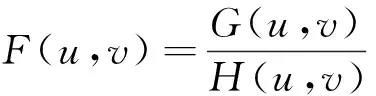
(5)

(6)

根据以上的推导公式可知，若己知退化图像的傅立叶变换以及“滤波”函数，便可先求得原始图像的傅立叶变换。在知道了原图像的傅里叶变换后，经反傅立叶变换便可求得原始图像f(x,y)。G(u,v)除以H(u,v)起到了反向滤波的作用。若考虑噪声影响，则有

(7)

其中，N(u,v)是噪声n(x,y)的傅里叶变换。

3 维纳滤波

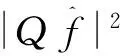
(8)

(9)

其中，E[·]表示数学期望。

Rf=E(ffT).

(10)

Rn=E(nnT).

(11)

根据上述定义可知，Rf和Rn均为正定对称矩阵，根据式(5)有

(12)

根据式(9)有频域维纳滤波公式如下：

(13)

γ=1时，得到的是标准维纳滤波器。

4 实验和结论

下面是假设已知退化的先验知识，图3为相机和物体的相对运动为20时捕获的模糊图像，图4是高斯模糊图像(σ=0.0001,μ=0)，其中σ,μ分别表示均方差和均值。从复原的效果来看，若能准确地退化先验知识，使用维纳滤波对模糊图像进行还原，得到的还原图像效果较好。

图3 运动模糊图像

图4 高斯模糊图像

图5 运动模糊图像复原

图6 高斯模糊图像复原

大多数情况下，我们无法确定图像退化之前是怎样的，即无法准确获取精确的点扩散函数，只能进行估计，其结果是图像恢复的效果不理想。其主要原因是参数过大或过小。图7和图8分别是对图3和图4采用估计的点扩散函数进行复原得到的复原效果图。

图7 用估计点扩散函数复原运动模糊图像

图8 用估计点扩散函数复原高斯模糊图像

为了得到令人满意的复原图像，可以充分利用模糊图像自身的一些统计特性来增强图像的还原效果。图像的统计特征很多，对于退化图像，比较重要的统计特征是图像的自相关函数及噪声的自相关函数。图9和图10是采用图像的自相关函数和噪声的自相关函数作为维纳滤波的参数进行图像还原质量试验的效果图。从实验结果可知，结合图像自身自相关函数和噪声的自相关函数，可以有效地提高复原图像的效果。从还原后的效果图可以看出，对于运动模糊图像使用自相关函数统计特征恢复效果不如使用真实的点扩散函数，但效果相差不明显。而对于高斯模糊图像，使用自相关函数统计特征其恢复效果要好于真实点扩散函数作为参数的维纳滤波还原。由此，为了提高图像恢复的质量，可以结合图像自身的信息，利用图像的自相关函数和图像中噪声的自相关函数作为参数，进行维纳滤波图像的复原。

主要代码如下：

N=(v*prod(size(F))).^2;

COR1=fftshift(real(ifftn(N)));

I1=abs(fftn(im2double(F))).^2;

COR2=fftshift(real(ifftn(I1)));

w1=deconvwnr(b1,p1,COR1,COR2);%维纳滤波,其中COR1,COR2分别为噪声和原图像的自相关函数

图9 运动模糊图像复原

图10 高斯模糊图像复原

[1]Gonzalez R C,Woods R E,Eddins S L.数字图像处理(MATLAB版)[M].阮秋琦,等,译.北京:电子工业出版社,2005.

[2]李孟,夏兴华,张楠.一种改进的维纳滤波图像恢复方法[C].International Conference on Circuit and Signal Processing,2010.

[3]周维华.Wiener滤波图像复原[J].计算机工程与科学,2007(3):39-40.

[4]Moghaddam M E,JamzadM.Motion blur dentification images using fuzzy sels[J].IEEE International Symposium Processing and Information Technology,2005(5):862-866.

[5]季冰川.局部运动模糊图像恢复系研究和实现[D].赣州:江西理工大学,2008.

[6]孟飞飞,商书元.基于盲解卷积算法的纤维模糊图像复原[J].北京服装学院学报,2011(3):53-58.

[7]张莹.运动模糊车牌图像盲复原与识别方法研究[D].青岛:青岛科技大学,2014.

Study on Wiener Filtering for Restoration of Image

SUN Yin-hui1，SUN Ying-juan2

(1.College of Computer,Jilin Normal University,Siping Jilin 136000,China;2.College of Computer Science and Technology,Changchun Normal Uniniversity,Changchun Jilin 130032,China)

This paper analyzed the principle of wiener filtering detailedly and performed. simulation experiment with Matlab. The experimental results show that the choice of the point spread function (PSF) of image restoration based on wiener filtering has great effect on the restorational result,we can use the autocorrelation function of image and noise autocorrelation function to improve the quality of image of reduction.

autocorrelation function;Wiener filter;image restoration;point spread function

2016-07-11

吉林省教育厅科技计划基金资助项目“基于计算机味觉的白酒质量评价体系和模式识别研究”(2012481)；吉林省教育厅科技计划基金资助项目“应用人工智能分析农民市民化的有效路径”(2013250)；吉林省教育厅科技计划基金资助项目“智能分类方法及其在疾病诊断中的应用研究”(2014249)；吉林省教育厅科技计划基金资助项目“智能推荐菜品平台研究”(2015367)；吉林省发展改革委工业技术研究和发展计划项目“基于关联度的智能点餐系统研究与开发”(2014Y101)。

孙英慧(1975- )，女，副教授，博士研究生，从事人工智能和图像处理研究。

TP391

A

2095-7602(2016)10-0030-04