高阶耦合Burgers方程的显示精确解

曹生让

(江苏联合职业技术学院南京分院，江苏南京 210019)



高阶耦合Burgers方程的显示精确解

曹生让

(江苏联合职业技术学院南京分院，江苏南京 210019)

本文利用一阶常微分扰动系统，借助于Mathematica的符号运算功能，构造了高阶耦合Burgers方程的显示解，得到了sech2和tanh型的孤子解、周期解、有理解等。

偏微分方程；高阶耦合Burgers方程；显示精确解

近年来，对单个孤立子模型的研究已经相当完善，关于耦合的孤子体系研究，得到了人们的普遍关注并发现了许多新的孤子解.目前，人们已经研究出许多有效的求解方法，例如反散射方法、Hirota双线性法、Backlund变换法、Darbox变换法、Jacobi椭圆函数法、Tanh函数展开法、直接代数法、参数假设法等.但是，利用一些方法得到方程解的类型不能令人满意.本文将用一种新的“扰动”方程统一构造非线性发展方程的显示解.

Burgers方程是模拟冲击波的传播和反射的非线性发展方程，单个Burgers方程ut+uxx+2uux=0是非线性系统中最重要的模型之一.近年来，一些推广的Burgers方程已经被提出，并得到了深入的研究.高阶耦合Burgers方程与单个Burgers方程一样，被广泛地应用在众多物理领域，例如不可压缩非粘性两层流体方面等.本文研究高阶耦合Burgers方程如下：

给出扰动方程

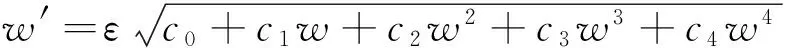
(3)

其中,是ξ的函数，ε=1或ε=-1，(3)式解的具体形式参见文献[1].首先，对方程组(1)和(2)作如下的变换：

其中，ξ=x+λ1y+λ2t，则有：

通过平衡(6)(7)中最高阶导数与非齐次项，可假设(5)(6)具有如下形式的解：

其中，=(ξ)，并且

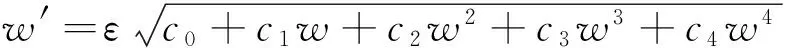
(10)

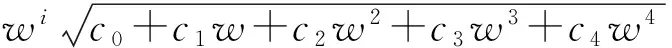
(11)

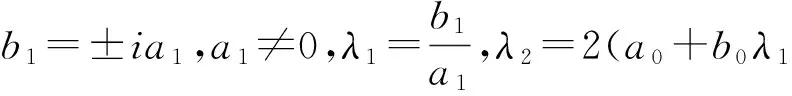
(Ⅰ)当c3=c0=c1=0时，

(12)

(13)

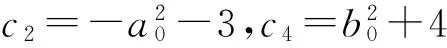
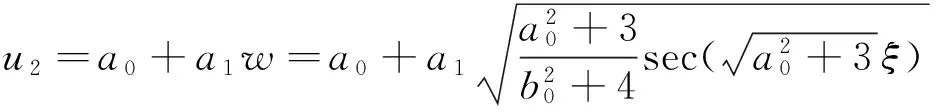
(14)

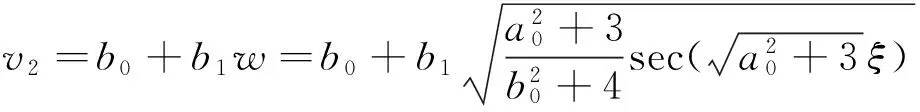
(15)

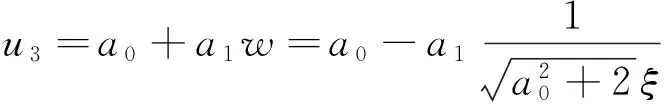
(16)

(17)

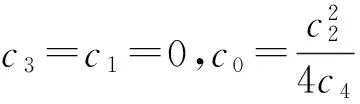
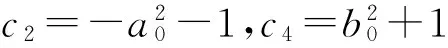
(18)

(19)

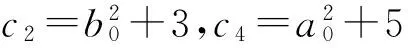
(20)

(21)

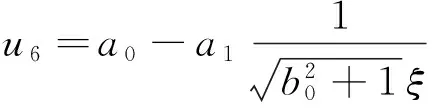
(22)

(23)

(Ⅲ)当c3=c1=0时，

(24)

(25)

(26)

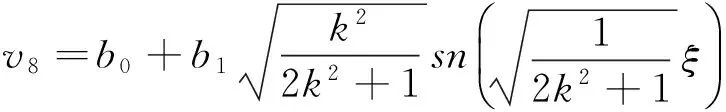
(27)

当k→1时，周期解(24)(25)退化为钟状孤立子解，周期解(26)(27)退化扭状孤子解.

(Ⅳ)当c4=c0=c1=0时，

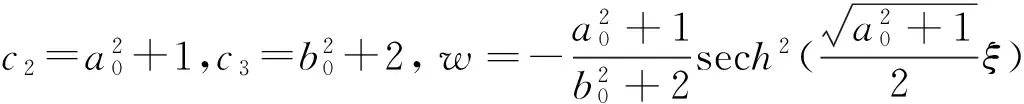
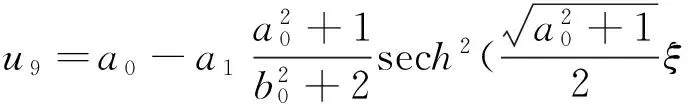
(28)

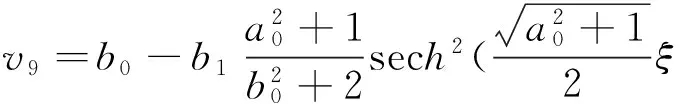
(29)

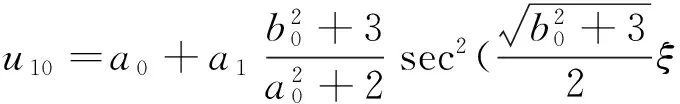
(30)

(31)

(32)

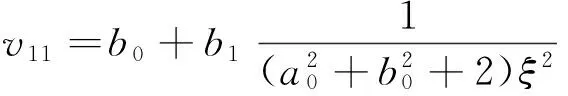
(33)

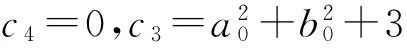
(34)

(35)

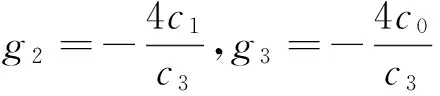
综上所述，本文通过引入“扰动”方法对非线性发展方程进行求解，得到了高阶耦合Burgers方程的多种形式的显示精确解，如钟状孤立子解、扭状孤立子解、椭圆函数解等，该方法可以用于其它非线性方程或方程组的求解.

[1]周钰谦,张健,刘倩.耦合Klein-Gordon-Schrodinger方程显示解的统一构造[J].四川师范大学学报:自然科学版,2006(2):166-170.

[2]王小芳.四波耦合微振动光学测量的研究[D].南京:南京师范大学,2006.

[3]张解放,戴朝卿,杨琴.(2+1)维Eckhaus型色散方程的新孤波解[J].浙江师范大学学报,2005(2):144-148.

[4]Fukuda I,Tsutsumi M.On coupled Klein-Gordon-Schrodinger equations[J].Math Anal Appl,1978(2):358-378.

[5]Svinolupov S I,Khabibullin I T.Integrable boundary conditions for many-component burgers equations[J].Math Notes,1996(6):671-680.

[6]Tang Xiaoyan,Lou Senyue.Variable separation solutions for the (2+1)-Dimensional Burgers Equation[J].China Phys Lett,2003(3):335-337.

[7]Foursov M V.On integrable coupled Burgers-type equations[J].Phys Lett A,2000(1):57-64.

[8]张辉群.耦合Klein-Gordon-Schrodinger方程的孤立波解[J].数学物理学报,2002(3):332-335.

[9]范恩贵.可积系统和计算机代数[M].北京:科学出版社,2004.

New Explicit Solutions of Higher Order Coupled Burgers Equations

CAO Sheng-rang

(Branch of Nanjing，Jiangsu Union Technical Institute,Nanjing Jiangsu 210019,China)

In this paper,by using the one order ODE as the disturbance equation and the symbolic toolbox of Mathematica,the solutions of higher order coupled Burgers equations are constructed,and a lot of new explicit solutions are obtained,including the solutions of the type of sech2and tanh,periodic solutions and rational solutions,etc.

partial differential equation;higher order coupled Burgers equations;explicit solutions

2016-05-22

曹生让(1982- )，男，讲师，硕士，从事微分方程研究。

O175.2

A

2095-7602(2016)10-0001-04