Dullin-Gottwald-Holm浅水波系统中具椭圆对称的自相似解
2016-12-12王昊
王 昊
(西北大学 数学学院,陕西 西安 710127)
·数理科学·
Dullin-Gottwald-Holm浅水波系统中具椭圆对称的自相似解
王 昊
(西北大学 数学学院,陕西 西安 710127)
运用椭圆对称和分离变量法研究了二分量Dullin-Gottwald-Holm浅水波系统,得到了具有椭圆对称和drift结构的自相似解以及一般形式的自相似解。通过构造Emden方程,研究了解的全局存在性以及有限时间的爆破现象。
DGH浅水波系统;椭圆对称;分离变量法;自相似解
在数学物理研究中,精确解的构造可以有效帮助刻画系统的一些非线性现象。1993年,Makino用分离变量法得到了Euler方程和Navier-Stokes方程的径向对称解[1]。在径向对称中,所有流体粒子的速度方向均指向或远离原点且距原点等距的粒子速度大小相同。与径向对称不同的是,椭圆对称中沿不同坐标轴方向,速度分量的变化可以各不相同。受文献[2]的启发,本文主要研究如下的二分量Dullin-Gottwald-Holm (DGH)系统:
(1)
该系统描述了具有非零旋度的浅水波运动,可以从二维Euler方程中利用渐进展开的方法得到。其中u=u(t,x)表示x方向的流体速度,ρ=ρ(t,x)刻画了自由表面[3-4]。当ρ=0时,二分量DGH系统(1)退化为DGH方程:
ut-utxx+γ uxxx+3u ux=σ(2uxuxx+u uxxx)。
该方程由Dullin, Gottwald和Holm在2001年所得到[5],同时指出DGH方程具有哈密顿结构,并给出了DGH方程的物理解释。更重要的是说明了DGH方程是一类非常重要的浅水波方程,可以描述浅水波运动。它和KdV方程一样存在光滑孤子解,也支持和Camasa-Holm方程类似的尖峰孤立子解[6-9]。
利用分离变量法,我们构造了二分量DGH系统 (1) 的具有椭圆对称和drift结构的自相似解。此外,通过研究相应的Emden方程,我们分析了自相似解的存在性和有限时间爆破现象[10-11]。
1 具有椭圆对称及drift结构的自相似解

构造DGH系统(1)的自相似解可分为以下几步,首先对(1)中连续性方程关于解(ρ(t,x), u(t,x)),我们有如下结论。
引理1 对连续性方程ρt+(ρ u)x=0,存在如下形式的解
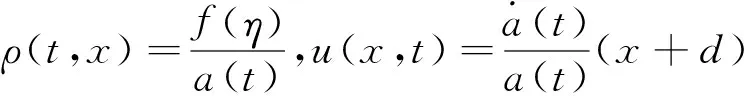
(2)
其中α,β为任意常数,f(η)≥0∈C1(R),d∈R,η=(x+d)2/a2(t)。
证 明 由自相似解的形式及椭圆对称的性质,设连续性方程的解为
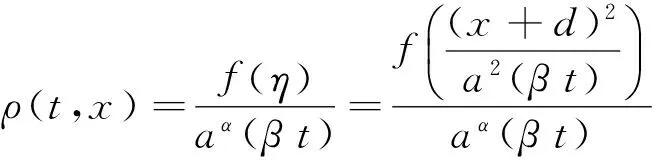

(3)
将式(3)代入连续性方程左端可得:
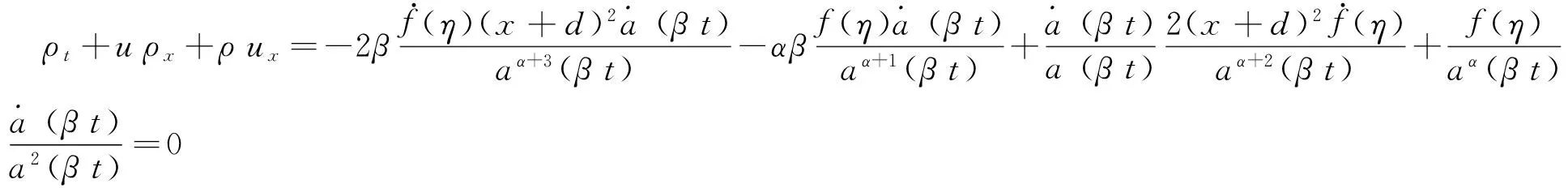
显然当α=1,β=1时,ρt+u ρx+ρ ux=0。
引理得证。
定理1 设函数a(t)是Emden方程

(a) 如果ξ>0,
(4)
(b) 如果ξ<0,a0>0,
(5)
(c) 如果ξ<0,a0<0,
(6)
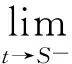
证 明 将式(3)代入式(1)中第一个方程,成立
ut-utxx+3u ux-σ(2uxuxx+u uxxx)+
γ uxxx+ρ ρx=ut+3u ux+ρ ρx=
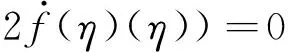
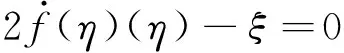
至此,已证得解(4),(5),(6) 满足DGH系统(1)。现可将原偏微分方程转化为求解常微分方程的初值问题,即
(7)
(8)
此外,因为a (t)是Emden方程的解,我们可根据参数ξ, a0和a1的取值不同,对a (t)的性质做如下分类:
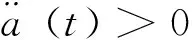
(9)

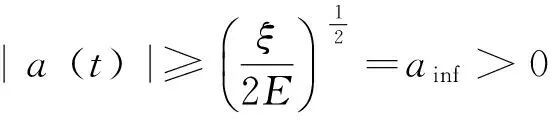
(10)
即a(t)存在下界。
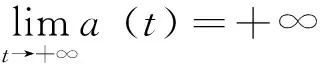
(1.2)当a1<0,存在以下两种可能:
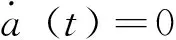

由瑕积分性质可知,等式右边的瑕积分收敛,但是当t→+∞时左边无界,出现矛盾,所以a (t)无界。
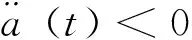
由不等式(10)可得a (t)≤-(ξ/2E)1/2<0,即a (t)存在上界。我们同样可以分为a1>0和a1<0两种情形,采用类似于情形(1)中的分析,可得相应结论。
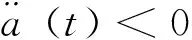
(3.1)当E>0时,由能量守恒方程(9)可得
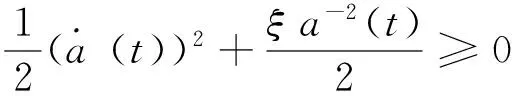
即
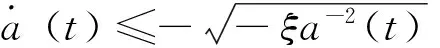
或
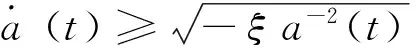
且
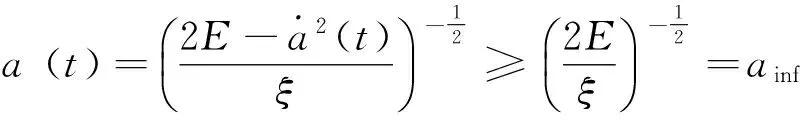
由假设ξ<0, E>0可知ainf<0。
(3.2)当E<0时,由能量守恒方程(9)可得
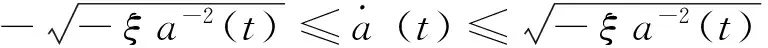
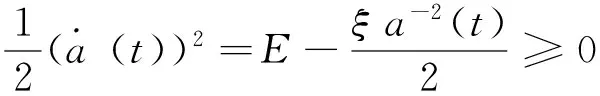
即-ξ a-2(t)/2≥-E>0,则00。
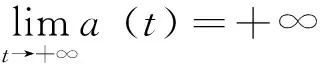
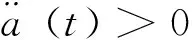
令b (t)=-a (t),可构造Emden方程
证法与情形 3) 类似。
证毕。
由能量守恒方程 (9),我们分别令ξ=1>0和ξ=-1<0,可以描绘出势能ξ a-2(t)/2的变化趋势。
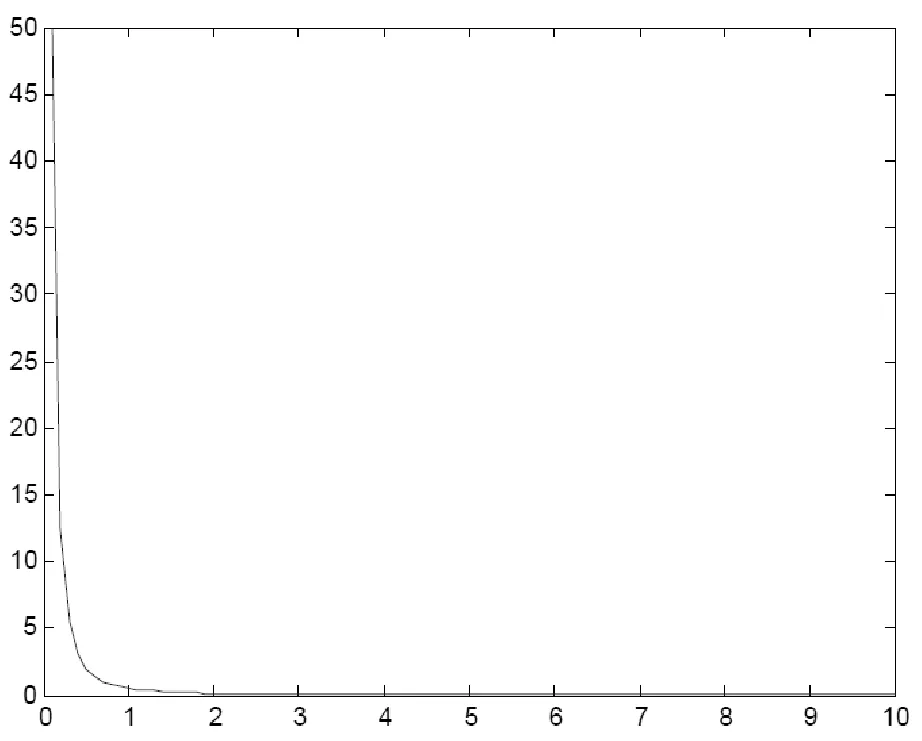
图1 当ξ=1时,势能曲线图Fig.1 Curve for potential energy with ξ=1
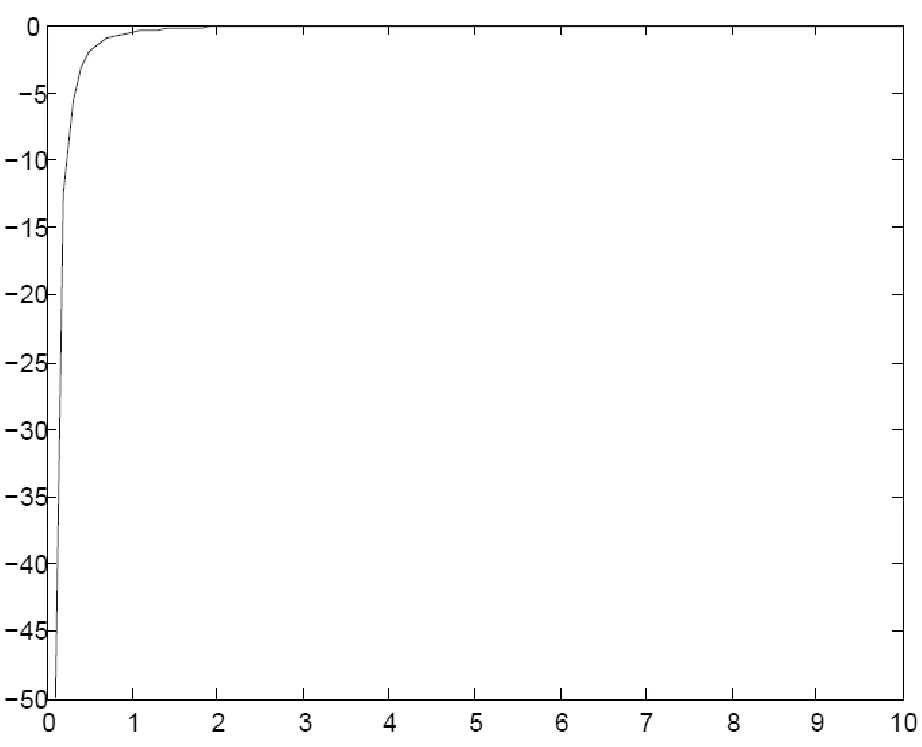
图2 当ξ=1时,势能曲线图Fig.2 Curve for potential energy with ξ=-1
2 一般形式的自相似解
在这一节中,我们主要研究二分量DGH系统(1)中具有一般形式的自相似解。
引理2 对连续性方程ρt+(ρ u)x=0,存在如下形式的解
(11)
其中α,β为任意常数且α·β=1,f(η)≥0∈C1(R),d∈R,η=(x+d)/aα(β t)。
证 明 将式(11)代入式(1)中连续性方程,可得
由α·β=1,则ρt+u ρx+ρ ux=0。
引理得证。
定理2 设函数a(s)是Emden方程
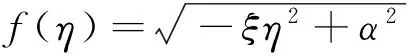
(a) 如果ξ<0时,
(12)
(b) 当ξ>0, a0>0时,

(13)
(c)当ξ>0, a0<0时,
(14)
证 明 将式(11)代入式(1)中DGH方程的左端,可得
ut-utxx+3uux-σ(2uxuxx+uuxxx)+γuxxx+
ρρx=ut+3uux+ρρx=
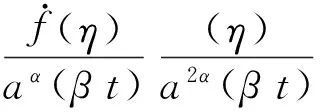
当β=3时,上式中间两项可以消去,可化为
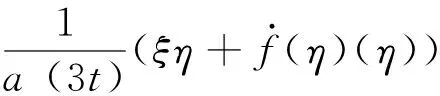
那么我们可将原偏微分方程转化为求解常微分方程的初值问题,即
(15)
(16)
对Emden方程
中ξ, a0, a1的不同取值进行讨论,可得到解的存在性及爆破现象。分析方法与定理1类似。
[1] MAKINO T. Exact solutions for the compressible Euler equation [J]. Journal of Osaka Sangyo University Natural Sci, 1993, 95:21-35.
[2] YUEN Manwai. Self-similar solutions with elliptic symmetry for the compressible Euler and Navier-Stokes equation in RN[J].Commun Nonlinear Sci Numer Simul, 2012, 12:4523-4528.
[3] HAN Yanwu, GUO Fei, GAO Hong-jun. On solitary waves and wave-breaking phenomena for a generalized two-component integrable Dullin-Gottwald-Holm system [J].J Nonlinear Sci, 2013, 23:617-656.
[4] GUO Fei, GAO Hongjun, LIU Yue. On the wave-breaking phenomena for the two-component Dullin-Gottwald-Holm system [J]. J London Math Soc, 2012, 3:810-834.
[5] DULLIN H, GOTTWALD G, HLOM D. An integrable shallow water equation with linear and nonlinear dispersion[J].Phys Rev Lett, 2001, 87:194501-194504.
[6] DULLIN H, GOTTWALD G, HOLM D. Camassa-Holm, Korteweg-de Vries and other asymptotically equivalent equations for shallow water waves [J]. Fluid Dyn Res, 2003, 33:73-95.
[7] DULLIN H, GOTTWALD G, HOLM D. On asymptotically equivalent shallow water wave equations [J]. Phys D, 2004, 190:1-14.
[8] TIAN Li-xin, GUI Gui-long, LIU Yue. On the well-posedness problem and the scattering problem for the Dullin-Gottwald-Holm equation [J]. Commun Math Phys, 2005, 257:667-701.
[9] MUSTAFA D. Existence and uniqueness of low regularity solutions for the Dullin-Gottwald-Holm equation [J].Commun Math Phys, 2006, 265:189-200.
[10] YAN Lu, SHI Zhenhua, WANG Hao, et al. Invariant subspaces and generalized functional separable solutions to the two-component b-family system [J]. Acta Mathematica Scientia, 2016, 36:1-13.
[11] YUEN Manwai. Self-similar blowup solutions to the 2-component Camassa-Holm equations [J]. J Math Phys, 2010, 51:581-604.
(编 辑 亢小玉)
Self-similar solutions with elliptic symmetry for the Dullin-Gottwald-Holm shallow water system
WANG Hao
(School of Mathematics, Northwest University, Xi′an 710127, China)
In this paper, elliptic symmetry and separation method are employed to study the two-component Dullin-Gottwald-Holm shallow water system, from which the self-similar solutions are obtained admitting the elliptic symmetry with a drift structure and self-similar solutions with general form. By constructing the Emden equation, investigations are given to show the global existence and finite-time blowup phenomenon.
Dullin-Gottwald-Holm shallow water system; elliptic symmetry; separation method; self-similar solutions
2016-03-11
国家自然科学基金资助项目(11471260)
王昊,男,陕西咸阳人,从事数学物理和可积系统的研究。
O175.2
A
10.16152/j.cnki.xdxbzr.2016-05-003
