带有黏性辐射流体系统解的正则性
2016-12-12孔春香
孔春香
(延安大学 数学与计算机科学学院, 陕西 延安 716000)
·数理科学·
带有黏性辐射流体系统解的正则性
孔春香
(延安大学 数学与计算机科学学院, 陕西 延安 716000)
考虑了欧拉坐标下一维黏性辐射流体系统的初始边界值问题,利用能量方法和一些基本不等式来估计解在H4空间中的整体存在性。在这里假设热传导系数的增长指数是非负常数,特别是热传导系数是常数也是成立的。
黏性辐射气体;整体解;先验估计
我们主要考虑通过自身耗散作用的一维可压缩的黏性热传导气体模型的初边值问题。在高温条件下,还要考虑这种气体模型受反作用的干扰和辐射作用的影响。根据动量、能量和质量守恒定律,在欧拉坐标下,这种反作用干扰运动模型表示如下:
ρt+(ρu)x=0,
(1)
ρ(ut+uux)+Px=(νux)x,
(2)

(3)
ρ(zt+uzx)=(dρzx)x-ρφz。
(4)

在高温条件下,压力和内部能量与密度和温度满足下面的关系:
(5)
这里正常数R,Cv,a代表完全气体系数,特殊热量系数,Stefan-Boltzmann常数。
初始条件:
(ρ,u,θ,z)(x,0)=(ρ0,u0,θ0,z0)(x)。
(6)
边界条件:
(u,θx,zx)|x=0=(u,θx,zx)|x=1=0。
(7)
初始条件和边界条件是相容的。

1 结 论



‖(ρtt,utt,θtt,ztt)(t)‖2+
‖(ρt,ut,θt,zt)(t)‖L2(0,T;H2(Ω))≤C。
2 局部解和先验估计
局部解的存在性文献[6]已给出,本节的主要任务是通过能量方法建立解的先验估计,从而完成解的整体存在性的证明。

则对任意固定的时间T>0,初始边界值问题(1)-(7)存在唯一的整体解
(ρ,u,θ,z)∈[0,1]×[0,T]满足

‖(ρt,ut,θt,zt)(t)‖L2(0,T;H1(Ω))≤C,
C-1≤ρ(x,t),θ(x,t)≤
C,0≤z(x,t)≤1,

‖(u,ρ,θ,z)(t)‖W1,∞(0,T;[0,1])+
‖ρt‖L∞(0,T;[0,1])≤C。
引理2 在定理1的假设下,对∀t>0,下面估计式成立

证 明 由方程(2)关于t求导得
νuxxt=ρutt+ρtut+ρtuux+ρutux+ρuuxt+Pxt。
(8)
式(8)两边乘以utt,在[0,1]上积分,利用引理1, Sobolev不等式,Cauchy不等式得
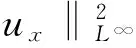

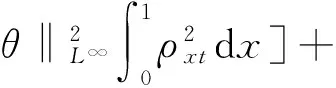
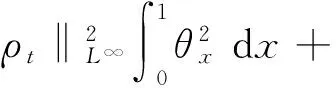

取ε非常小,于是有

根据引理1和Gronwall′s不等式,完成了引理2的证明。
引理3 在定理1的假设下,对∀t>0,下面估计式成立:
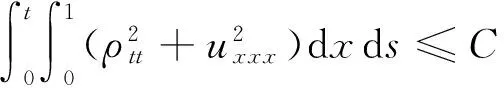
证 明 由方程(2)关于x求导得
νuxxx=ρxut+ρutx+ρxuux+
(9)
由引理1,2,Cauchy不等式,Poincare不等式得



(10)
由引理1,2,式(10),从而有
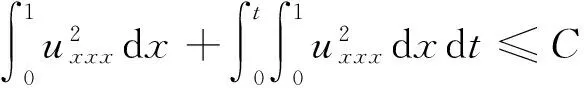
又由方程(1)关于x,t分别求导,由引理1,2得

引理4 在定理1的假设下,对∀t>0,下面估计式成立:

(11)
证 明 方程(1)关于t求导数,得
ρtt=-ρxtu-ρxut-ρtux-ρuxt。
由引理1,3, Cauchy不等式得

由方程(2)关于t求导得
νuxxt=ρutt+ρtut+ρtuux+ρutux+
ρuuxt+Pxt。
(12)

从而有


由引理1得

引理5 在定理1的假设下,对∀t>0,下面估计式成立:
(13)

(14)
证 明 方程(3)可以改写为
(Cvρ+4aθ3)θt+(Cvρ+4aθ3)uθx=

(15)
式(15)关于x,t求导乘以θtx,利用引理1~4,Young不等式
C(ε)[‖θt‖2‖ρxt‖2+

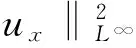
Cε[‖uxt‖2‖uxx‖2+

从而有

方程(4)可以重写为

(16)
类似的由式(16)关于x,t求导,其结果乘以ztx可以得到

利用引理1~10,在[0,t]上积分得

‖zxt‖2+‖ρxxt‖2+‖ρxx‖2]ds+

取ε充分小可得

引理6 在定理1的假设下,对∀t>0,下面估计式成立

证 明 方程(2)关于t求二次导得
ρuttt+2ρtutt+ρttut+ρttuux+2ρtutux+
2ρtuuxt+ρuttux+2ρutuxt+ρuuxtt+
(17)
式(17)两端乘以utt,在[0,1]上积分,并分部积分,利用式(1),引理1~3,Cauchy不等式,嵌入定理得



因此,有
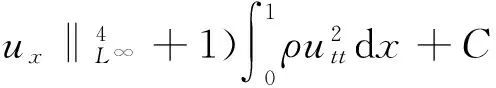
(18)
式(18)在[0,t]上积分得

利用Gronwall′s不等式,引理1~4,得到估计。
引理7 在定理1的假设下,对∀t>0,下面估计式成立

证 明 由方程(1)(2)(3)得
(Cvρ+4aθ3)θt+(Cvρu+4aθ3u)θx+

(19)
式(19) 关于x求导得,利用引理1、Cauchy不等式、Poincare不等式得





上式在[0,t]上积分得,利用引理1~7可得

引理8 在定理1的假设下,对∀t>0,下面估计式成立
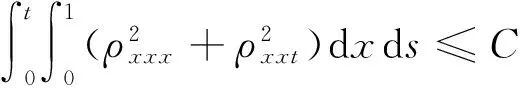
证 明 由方程(1),(2)得
νρxt+Rρθρx=-ν(2ρxux+uρxx)-
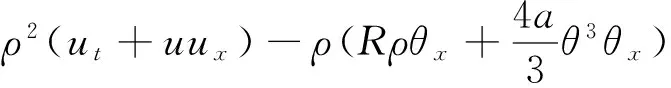
(20)
式(20)关于x求二次导数,乘以ρxxx在[0,1]×[0,t]上积分,利用上述引理1~7,Cauchy不等式得

(21)
其中由Sobolev不等式得






方程(1)关于x求二次导数,由引理1~7和式(21), Cauchy不等式得

引理9 在定理1的假设下,对∀t>0,下面估计式成立

(22)
证 明 式(9)关于x求导得
νuxxxx=ρxxut+2ρxutx+ρuxxt+
ρuuxxx+Rρxxxθ+3Rρxxθx+3Rρxθxx+
(23)
由式(23)、引理1~8、嵌入定理、Cauchy不等式得

由引理1~8得

由方程(3),(4)关于x求二次导数,引理1得
‖θtxx‖≤C(‖θx‖H3+‖ux‖H2+
‖ρx‖H1+‖zx‖H1+‖θt‖H1+‖ρt‖H1)。
(24)
‖ztxx‖≤C(‖θx‖H1+‖ux‖H1+
‖ρx‖H2+‖zx‖H3+‖zt‖H1)。
(25)
或者
‖θxxxx‖≤C(‖θx‖H2+‖ux‖H2+
‖ρx‖H1+‖zx‖H1+‖θt‖H1+
‖ρt‖H1‖θtxx‖)。
(26)
‖zxxxx‖≤C(‖θx‖H1+‖ux‖H1+
‖ρx‖H2+‖zx‖H2+‖zt‖H1+‖ztxx‖)。
(27)
由式(26),(27) ,引理5得

引理10 在定理1的假设下,对∀t>0,下面估计式成立

证 明 由方程(3),(4)关于t求导,引理1~7, 式(24)~(25)得
‖θtt‖≤C(‖ρt‖H1+‖θt‖H2+
‖ρtt‖+‖uxt‖+‖zt‖+‖ρx‖+
‖θx‖)≤C(‖θx‖H3+‖ux‖H2+
‖ρx‖H1+‖zx‖H1+‖ρt‖H1+
‖ρtt‖+‖uxt‖+‖zt‖),
(28)
或者
‖θtxx‖≤C(‖ρt‖H1+‖θt‖H1+
‖ρtt‖+‖uxt‖+‖zt‖+‖ρx‖+
‖θx‖+‖θtt‖),
(29)
‖ztt‖≤C(‖ρt‖H1+‖θt‖+‖zt‖H2+
‖ut‖+‖zx‖)≤C(‖θx‖H1+‖ux‖H1+
‖ρx‖H2+‖zx‖H3+‖zt‖H1+
‖θt‖+‖ut‖),
(30)
或者
‖ztxx‖≤C(‖ρt‖H1+‖θt‖+
‖zt‖H1+‖ut‖+‖zx‖+‖ztt‖)。
(31)
式(15)关于t求二次导数,乘以θtt在[0,1]上积分,利用引理1~9、Cauchy不等式、式(28)~(30)得

Cε-1‖θx‖L∞(‖utt‖2+‖ρtt‖2+
‖ut‖2‖θt‖2)+C(‖θxtt‖2+‖θxt‖2+
‖uxt‖2+‖uxtt‖2+‖ztt‖2)≤


‖θtx‖2)+Cε-1‖θttx‖2。
在[0,t]上积分,引理1~9得

(32)
式(16)两边关于t求二次导,结果乘以ztt在[0,1]上积分,分部积分,根据引理1~9,方程(1),得
从而有

(33)
由式(27),(32),(33),引理1~9, (13),(14) 可得
引理11 在定理1的假设下,对∀t>0,下面估计式成立

证 明 由式(24),(25),(32),(33),引理1~10得
‖θtxx‖≤C(‖ρt‖H1+‖θt‖H1+‖ρtt‖+
‖uxt‖+‖zt‖+‖ρx‖+‖θx‖+
‖θtt‖)≤C,
(34)
‖ztxx‖≤C(‖ρt‖H1+‖θt‖+
‖zt‖H1+‖ut‖+‖zx‖+‖ztt‖)≤C。
(35)
由式(34)-(35)-(25)-(26)得

式(20)关于x求导,结果乘以ρxxxx在[0,1]×[0,t]上积分,利用引理1~10,Cauchy不等式得

其中由引理1~11,Sobolev不等式得






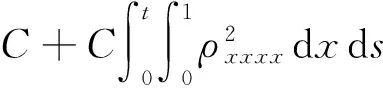
式(23)关于x求导数,利用引理1~10,嵌入定理得

从而可得

引理12 在定理1的假设下,对∀t>0,下面估计式成立:
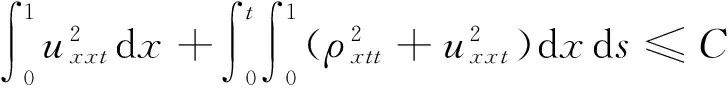
证 明 由方程(2)关于t求导得
νuxxt=ρutt+ρtut+ρtuux+ρutux+ρuuxt+Pxt。

从而有


(36)
方程(1)关于x,t求导,利用式(36),引理1~11, Cauchy不等式得

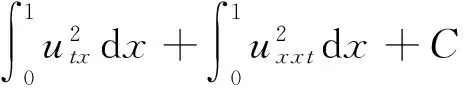
联立以上引理,我们完成了整体解存在性的证明。
[1] WANG Dehua. Large solutions to the initial-boundary value problem for planar magnetohydro-Dynamics[J]. J Appl Math,2003,63(4):1424-1441.
[2] QIN Xiaohong, WANG Yi.Large-time behavior of solutions to the inflow problem of full compressible Navier-Stokes equations[J]. J Appl Math,2011,43(1):341-366.
[3] DING Shijin,WEN Huanyao,YAO Lei,et al.Global spherically symmetric classical solution to compressible Navier-Stokes equations with large initial data and vacuum[J]. J Appl Math,2012,44(2):1257-1278.
[4] WEN Huanyao, ZHU Changjiang.Global classical large solution to Navier-Stokes equations for viscous compressible and heat-conducting fluid with vacuum[J]. J Appl Math,2013,45(2):431-468.
[5] JIANG Jie, ZHENG Songmu.Global well-posedness and exponential stability os solutions for the viscous radiative and reactive gas[J]. Z Angew Math Phys,2014,65(4):645-686.
[6] ZHANG Wen,ZHANG Jianwen.Global existence of solutions for the 1-D radiative and reactive viscous gas dynamics. Applications of mathematics[J], 2012,57(2):109-128.
[7] UMEHARA M,TANI A.Global solution to the one-dimensional equations for a self-gra-vitating viscous radiative and reactive gas[J].J.Differential Equations, 2007,234(2):439-463.
[8] YANAGI S.Asymptotic behavior of the solutions for one-dimensional equations of a viscous reactive gas[J]. J Indust Appl Math,2008,25(1):99-116.
[9] LEWICKA M,MUCHA P B. On temporal asymptotics for the pth power viscous reactive gas[J].Nonlinear Analysis,2004,57(7):951-969.
[10] DUCOMET B. A model of thermal dissipation for a one-dimensional viscous reactive and radiative gas[J]. Math Meth Appl Sci,1999,22(15):1323-1349.
[11] CEN G. David Hoff and Konstantina Trivisa, On the Navier-Stokes equations for exothermically reacting compressible fluids[J]. Acta Mathematicae Applicatae Sinica,2002, 18(1):15-36.
[12] QIN Yuming, HUANG Lan. Global existence and exponential stability for the pth power viscous reactive gas[J]. Onlinear Analysis,2012,73(9):2800-2818.
[13] GUO Boling, ZHU Peicheng.Asymptotic behavior of the solution to the system for a viscous reactive gas[J]. J Indust Appl Math, 1999,155(1):177-202.
[14] WEN Huanyao, ZHU Changjiang.Global classical large solutions to Navier-Stokes equations for viscous compressible and heat-conducting fluids with vacuum[J]. J Math Anal,2013,45(2):431-468.
(编 辑 亢小玉)
Regulary of solutions for radiative and reactive viscous gas dynamics
KONG Chunxiang
(College of Mathematics and Computer Science, Yan′an University, Yan′an 716000, China)
It was concerned with the initial-boundary problem of 1-D radiative and reactive viscous gas dynamics under Euler coordinate. The global existence of the solution in spaceH4is estimated by using the energy method and some basic inequalities. Assuming that the growth exponent of heat conductivity is allowed to be any nonnegative constant, in particular, constant heat conductivity is allowed.
radiative and reactive viscous gas; global solution; priori estimates
2016-04-16
陕西省自然科学基础研究计划基金资助项目(2014JM2-1003);延安大学校级科研计划基金资助项目(YDK2015-46)
孔春香,女,河南兰考人,从事偏微分方程研究。
O175.2
A
10.16152/j.cnki.xdxbzr.2016-05-006
