改进量子粒子群优化算法的神经网络模型负荷预测

张 兰

(1.西北工业大学 理学院,陕西 西安 710129;2.西安航空职业技术学院 基础课部, 陕西 西安 710089)



·数理科学·

改进量子粒子群优化算法的神经网络模型负荷预测

张 兰1,2

(1.西北工业大学 理学院,陕西 西安 710129;2.西安航空职业技术学院 基础课部, 陕西 西安 710089)

提出一种基于Levy飞行的量子粒子群优化算法并用于小波神经网络的训练,该算法采用基于Levy分布的飞行策略扩大粒子的搜索空间,使粒子易于逃离局部最优点。该算法克服了传统算法在神经网络训练过程中易于陷入局部最优、收敛速度慢等缺点,提高了神经网络的泛化能力。最后将改进的量子粒子群优化算法训练小波神经网络应用于电力系统负荷预测的模型,仿真结果表明改进的量子粒子群优化算法在神经网络训练上具有更高的预测精度。

Levy飞行;量子粒子群;神经网络;负荷预测

负荷预测是一个复杂的问题,其预测的准确性将影响到电力生产和电网安全运行等方面[1]。而影响负荷预测的常见因素如天气等经常具有随机性,使得预测模型呈现很大的非线性,因此负荷预测的技术就显得非常重要。传统的预测方法如线性回归、专家系统、模糊控制等算法的效果常常无法满足实际需要[2]。

神经网络强大的自主学习能力和良好的非线性映射能力使其广泛应用于负荷预测、故障诊断和系统辨识等方面[3]。然而传统的神经网络算法在进行网络训练时,具有学习效率低下、容易陷入局部极小值等缺点。近年来，许多学者致力研究于神经网络性能的提高,如Zhang等人[4]提出了小波神经网络(wavelet neural network, WNN),该算法是将小波变换理论和神经网络相结合,兼有了小波变换的局部化性质和神经网络的自主学习能力,所以具有较好的逼近能力。目前，小波神经网络在模型预测、系统辨识、故障诊断等领域取得了一些成果[5-6],然而其泛化能力一直是学术界的难点。

随着计算技术的快速发展,智能优化算法开始广泛应用于复杂工程领域的计算。粒子群优化算法(particle swarm optimization,PSO)[7]是由Kennedy和Eberhart在1994年提出的,该算法是通过模拟鸟群觅食行为来进行函数寻优,且具有参数少、鲁棒性高等优点。因此,采用PSO算法训练WNN模型能够更好的发挥神经网络的泛化能力。然而PSO算法在收敛后期粒子易失去多样性,出现早熟、陷入局部极小值点等缺点。孙俊等[8-9]从量子系统出发提出一种量子粒子群优化算法(quantum behaved particle swarm optimization,QPSO),该算法中粒子具有更高的随机性,也就意味着QPSO算法比传统的PSO算法具有更好的全局搜索能力。在QPSO-WNN 模型进行负荷预测方面,文献[10]进行了探索,也取得了较好的预测效果,但是在迭代后期,由于粒子对前期运动轨迹的记忆,限定了种群的搜索空间,使得预测结果不是十分理想,因此,可以对QPSO算法进行改进以提高算法的收敛性能和精度。比如,文献[11]提出了对平均最优位置加权的量子粒子群优化,提高了算法的收敛速度;Coelho等[12]提出了采用Gauss变异算子修正QPSO并应用于求解PID控制问题,修正后的算法增强了全局搜索能力;Peng等[13]利用Levy分布对QPSO算法中的全局最优值进行变异,Levy分布的尾翼相比于高斯分布和柯西分布更宽,因此具有更好的扰动能力,从而增加了粒子跳出局部最优的能力。

本文借鉴文献[13]中的Levy分布,对QPSO算法进行改进,将基于Levy分布的Levy飞行策略应用于QPSO中,让粒子在更大的解空间中进行搜索,使粒子更容易跳出局部最优点,而且收敛速度和性能都有所提高。最后将改进的QPSO算法进行小波神经网络训练,并将其应用于电力系统的负荷预测中。对实际算例的仿真分析,验证了该算法具有更高的预测精度。

1 QPSO算法及其改进

1.1 QPSO算法

粒子群算法是一种基于群体的随机优化技术,是对鸟类的群体聚集行为进行仿真研究启发而得到的。PSO算法将每个可能产生的解表述为一个粒子,所有粒子在搜索空间中以一定速度飞行,粒子的运动轨迹用每个粒子的位置和速度来描述。但是,粒子在寻优中随机性不高,导致容易收敛到局部最优点。2004年孙俊等人在量子系统中提出了一种量子粒子群优化算法,该算法中的粒子具有量子行为,其运动状态是由波函数来确定,粒子在量子δ势阱的基础上不断的靠近局部吸引点pi(t),粒子在空间某位置的概率由薛定谔方程确定。因此采用蒙特卡洛模拟得到粒子的运动轨迹用如下方程确定:

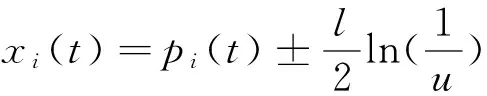
(1)

其中,xi(t)为个体当前最优位置,u为[0, 1]之间的均匀分布随机数,±是由u的大小决定的,当u>0.5时,取+号,其他情况取-号;局部吸引点pi(t)由式(2)确定:

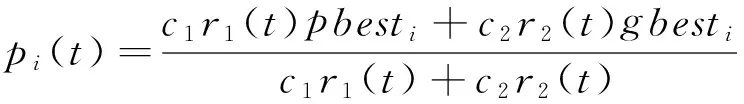
(2)

l为势阱长度，由式(3)确定:

li(t)=2β|mbesti-xi(t)|。

(3)

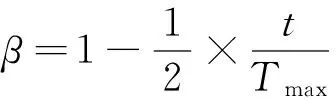
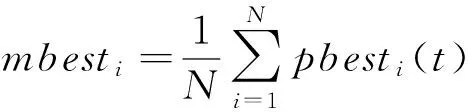
(4)

其中:N为种群数,因此,QPSO算法中粒子的进化方程最终为如下式子:

xi(t+1)=

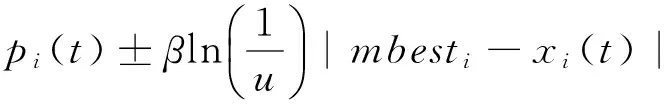
(5)

1.2 Levy飞行原理

Levy飞行是一种随机过程,行走的步长服从Levy分布,它符合自然界的大部分生物的搜索行为,在进行大规模搜索寻优时, 它可以进行多数粒子的短距离局部搜索和少数粒子的长距离全局搜索 不仅能扩大种群的搜索空间,同时也能提高全局搜索性能,因次,一些学者在优化算法中引入Levy飞行策略并取得了较好的性能[14-17]。

Levy飞行的步长服从Levy 分布,其概率密度函数通常以如下形式出现

(6)

一般都是对其进行简化和傅里叶变换,得到幂指数形式的概率密度函数如下所示：

Levy～μ=t-λ;1<λ<3。

(7)

其中:λ为幂指数,式(7)服从Levy分布式是一个带有宽尾的概率分布，在程序计算L(λ)时,通常采用Mantegna提出的模拟Levy飞行步长的计算公式[18]：

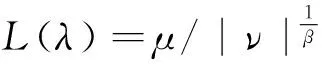
(8)

(9)

通过式(8)、(9)就可以计算出Levy飞行步长L(λ)。

1.3 改进的QPSO算法

在QPSO算法中,随着粒子迭代次数的增加,种群的多样性减少,相似的粒子会大大缩减种群的搜索空间,粒子陷入局部最优后很难跳出来。采用Levy飞行策略进行搜索可以扩大粒子搜索空间,因此,Richer等人[19]最早在PSO算法中对于个体最优引入了Levy分布,提高了搜索效率。本文在前述文献的基础上采用Levy飞行策略对QPSO算法进行改进,利用Levy飞行独特的随机游走机制进行搜索,以期扩大粒子的搜索空间,并增加了种群的多样性。基于该策略的改进算法中需要将原算法中的式(5)更新为

(10)

其中：L(λ)中取λ=2。本文将采用Levy飞行搜索的QPSO算法,记为LQPSO。

2 LQPSO算法训练WNN

2.1 小波神经网络概述

WNN是用小波函数替代神经网络的激活函数而得到,具有小波变换和神经网络的优点,它有很强的自主学习能力、函数逼近能力和较快的学习速度。三层的小波神经网络拓扑如图1所示。

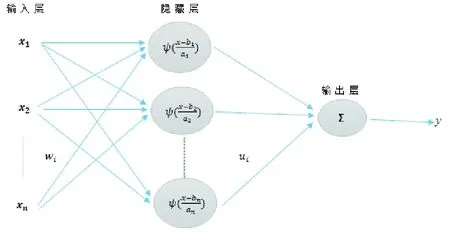
图1 小波神经网络的结构Fig.1 The structure of WNN

其中xi(i=1,2,…,N)为输入层,隐藏层激活函数采用小波基函数,文中取Morlet为基函数;y(x)为WNN的输出,wi(i=1,2,…,N)为输入层与隐藏层的神经元间的权值,ui为隐藏层与输出层的神经元间的权值。

2.2 LQPSO算法训练WNN

QPSO-WNN网络训练的本质就是网络的权重和阀值不断调整的过程。QPSO用于WNN训练时,网络的权重和阈值由粒子的位置向量xi代表,粒子的最佳适应度函数用网络训练的均方误差来表示:

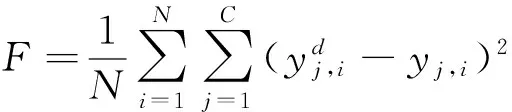
(11)

LQPSO算法训练WNN的步骤:

Step1 确定WNN模型结构:输入层,隐含层,输出层的数目；

Step2 初始化:确定粒子数N=30,粒子维数20,最大迭代代数Tmax=200, 最佳精度g;

Step3 通过公式(11)评价每个粒子i对训练样本的适应度;

Step4 通过公式(2),(4),(10)计算粒子i经Levy飞行后的达到的最佳位置pbesti,以及当前最佳适应度值,并将其与全局最优位置gbesti的最佳适应度值进行对比,若较好,则用其替换全局最优位置,并记录当前适应度值;

Step5 判断是否达到最大迭代次数,否则返回步骤2;

Step6 不断更新粒子,确定最佳网络参数;

Step7 输入训练参数,进行WNN模型的负荷预测;

Step8 反复训练,直到达到满意的预测精度。

3 LQPSO-WNN模型用于负荷预测仿真

3.1 数据来源和模型结构

本实验所用数据来源于网站:http://www.ferc.gov/market-oversight/mkt-electric/overview.asp中某城市的负荷数据。由于负荷数据具有很大的随机性,原则上,选取历史负荷数据越多,负荷预测的精确度就会越高。因此,在实际应用中,常常选择具有代表性的数据,并对数据做预处理。一般的处理方法有数据的归一化,使其位于[0,1]之间;对错误数据进行剔除;对缺失数据进行前后两个数据取平均值。在负荷预测中,负荷的数据主要受历史数据和天气的影响,另外,工作日和周末的负荷模式差异比较大。因此应该将负荷数据在工作日和周末的独立预测。QPSO-WNN网络模型如表1。

3.2 LQPSO-WNN 预测结果及分析

本实验在MATLAB-R2013a上进行,实验结果采用绝对误差(absolute percentage error,APE)和平均绝对误差(mean absolute percentage error,MAPE)作为检验预测的负荷值和实际的负荷值之间差异的标准。

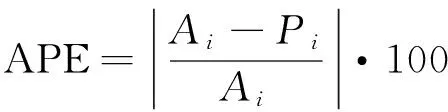
(12)

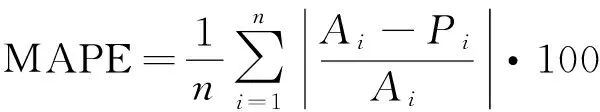
(13)

其中,Ai代表实际的负荷值,Pi代表预测的负荷值,n代表小时数。

表1 采用的网络结构模型

本文任意选中其中一天24小时整点的数据作为检验网络的泛化能力,分别采用QPSO-WNN和LQPSO-WNN用于负荷预测,并将得到的预测值与实际的电力负荷值作比较,得到预测结果分别如图2和图3所示,横坐标为时间,纵坐标为负荷值。

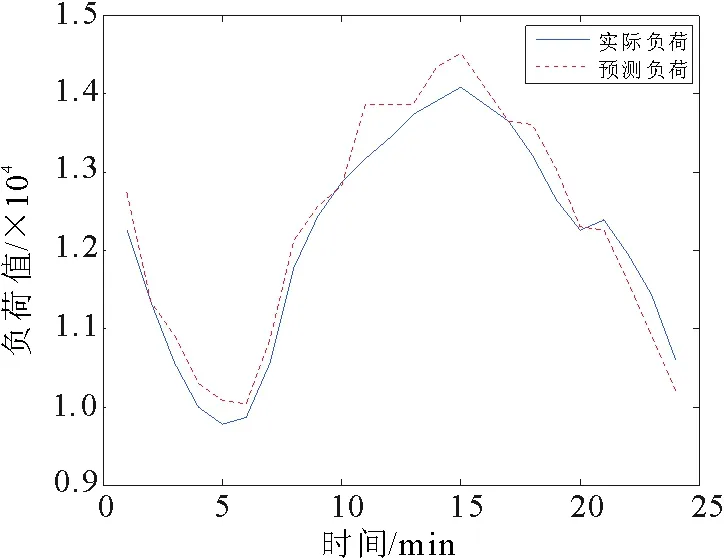
图2 LQPSO-WNN预测结果Fig.2 The result of improved QPSO-WNN

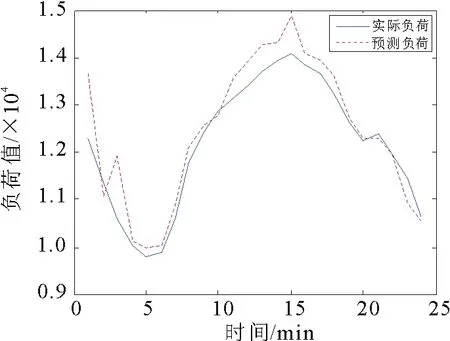
图3 QPSO-WNN预测结果Fig.3 The result of QPSO-WNN

分析比较可知,用LQPSO-WNN方法的负荷预测值和实际值的拟合度相对较高。两种模型的绝对误差APE比较如表2,由表2可知,未改进的QPSO-WNN模型的最大绝对误差达到12.452 6%,而改进之后的最大绝对误差为5.281 1%。改进后的模型降低了负荷预测的绝对误差。由表3可知QPSO-WNN模型MAPE为3.031 2%,而LQPSO-WNN模型的MAPE为2.381 5%。由此可以看出LQPSO-WNN模型提高了预测精度。另外,在表3中可以发现改进的模型迭代时间更短,计算效率更高。因此,本文提出的算法在进行负荷预测时具有优越性和高效性。

表2 两种网络结构模型的绝对误差(APE)对比

Tab.2 Comparisons of APE between two network structures adopted

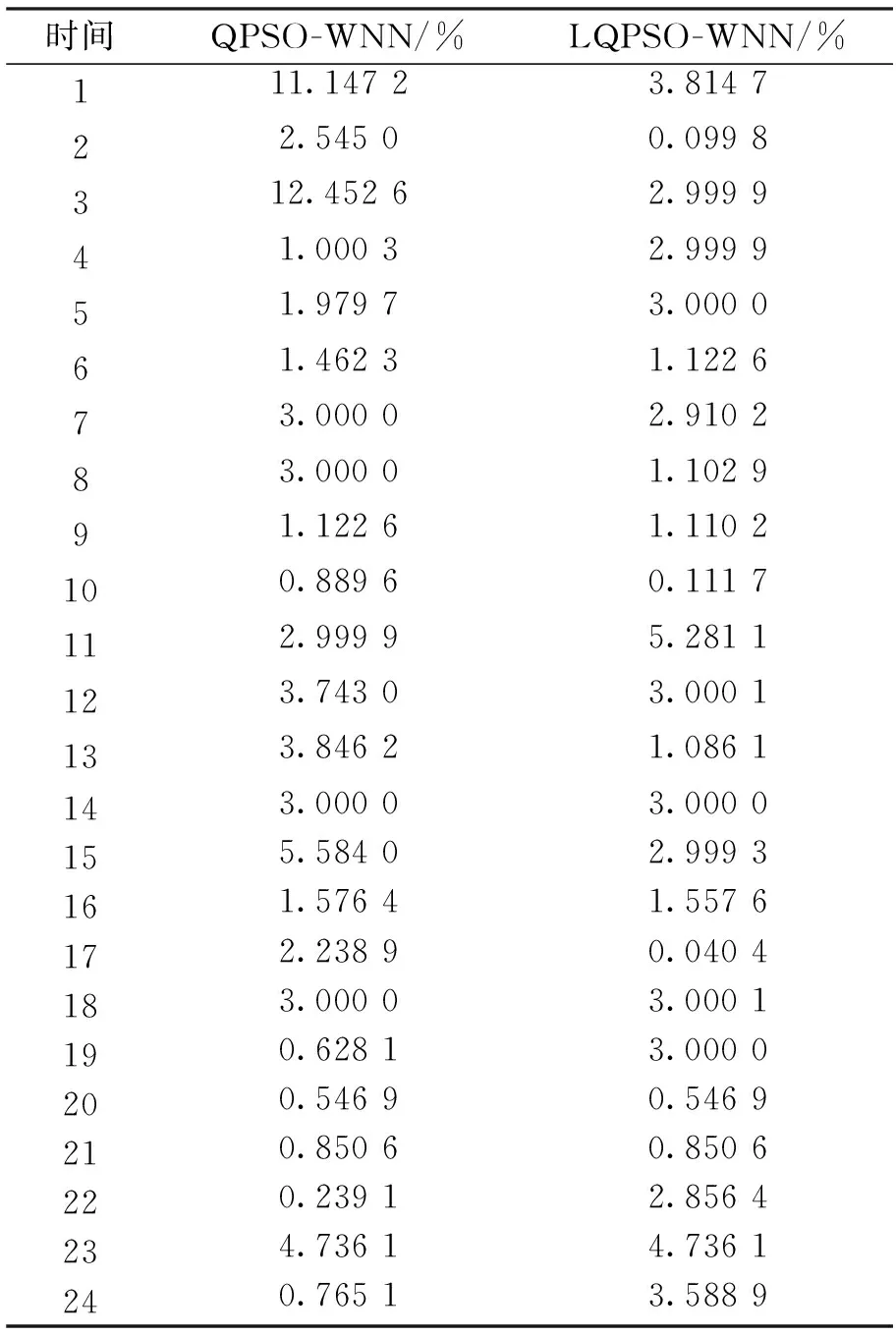
时间QPSO-WNN/%LQPSO-WNN/%111.14723.814722.54500.0998312.45262.999941.00032.999951.97973.000061.46231.122673.00002.910283.00001.102991.12261.1102100.88960.1117112.99995.2811123.74303.0001133.84621.0861143.00003.0000155.58402.9993161.57641.5576172.23890.0404183.00003.0001190.62813.0000200.54690.5469210.85060.8506220.23912.8564234.73614.7361240.76513.5889

表3 两种网络结构模型的迭代时间和预测误差(MAPE)的对比

Tab.3 Comparisons of iteration time and MAPE between two network structures adopted

模型结构迭代时间MAPE/%QPSO-WNN1943.0312LQPSO-WNN1572.3815

4 总 结

本文首先对QPSO算法进行改进,提出了基于Levy飞行的LQPSO算法,该算法采用Levy飞行搜索来更新粒子位置,扩大了粒子的搜索空间,使搜索效率最大化,从而避免粒子陷入局部最优点,提高了全局搜索性能和速度,并将LQPSO算法进行训练WNN模型。最后将训练好的LQPSO-WNN模型应用于电力系统的负荷预测仿真试验,负荷预测结果表明LQPSO算法在WNN的训练中不仅具有较快的收敛速度,而且还提高了负荷预测的精度。

[1] 康重庆,夏清,刘梅.电力系统负荷预测[M].北京:中国电力出版社,2007:3-5.

[2] MOGHRAM I, RAHMAN S. Analysis and evaluation of five short-term load forecasting techniques [J]. Proceedings of the IEEE Transaction on Power Systems, 1989,4(4):1484-1491.

[3] 梁艳春,聂义勇.从科学方法论看人工神经网络研究的发展[J].吉林大学学报(信息科学版), 2001,20 (1):59-62.

[4] ZHANG Q. BENVENISTE. A wavelet networks [J]. IEEE Transactions of Neural Networks, 1992, 3(6):889-898.

[5] ZHANG Q. Using wavelet network in non parametric estimation [J].IEEE Transactions on Neural Networks, 1997, 8(2): 227-236.

[6] SZU H, TELFER B, KADAMBE S. Neural network adaptive wavelets for signal representation and classification[J]. Optical Engineering, 1992, 36(9):1907-1916.

[7] KENNEDY J, EBERHART R C. Particle swarm optimization[C]. Proceedings of the 1995 IEEE International Conference on Neutral Networks. Piscataway, NJ: IEEE Press, 1995: 1942-1948.

[8] SUN J, FENG B, XU W.B. Particle swarm optimization with particle having quantum behavior [C].Proceedings of Congress on Evolutionary Computation, Portland, USA：IEEE Press, 2004,1: 325-331.

[9] SUN J, XU W B, FENG B. Adaptive parameter control for quantum behaved particle Swarm optimization on individual level [C].Proceedings of IEEE International Conference on Systems, Man And Cybernetics, Piscataway：IEEE Press, 2005:3049-3054.

[10] TIAN S, LIU T J. Short term load forecasting based on FBFNN and QPSO[J]. Power and Energy Conference, 2009, 4:1-4.

[11] XI M L, SUN J, XU W B. An improved quantum behaved particle swarm optimization with weighted mean best position[J]. Applied Mathematics and Computation,2008,11: 751-759.

[12] COELHO L S, NEDJAH N, MOURELLE L M. Gaussian quantum behaved particle swarm optimization applied to fuzzy PID controller design[J]. Computational Intelligence, 2008,201:1-15.

[13] PENG Y M, XIANG Y, ZHONG Y B. Quantum-behaved particle swarm optimization algorithm with levy mutated global best position[J]. Fourth International Conference on Intelligent Control And Information Processing, 2013,7:529-534.

[14] LIU C P, YE C M. Bat algorithm with the characteristics of Levy flights [J]. CAAI Transactions On Intelligent Systems, 2013, 8(1): 240-246.

[15] 刘晓勇.带有Levy flight机制的引力搜素算法[J].计算机科学与探索,2014,8(10)1239-1245.

[16] 朱晓恩,郝欣,夏顺仁.基于Levy flight的特征选择算法[J].浙江大学学报(工学版),2013,47(4):638-643.

[17] 严小飞,叶东毅.基于Levy飞行的改进菌群觅食算法[J].计算机系统应用,2015,24(3): 124-132.

[18] 张前图,房立清, 赵玉龙. 具有Levy飞行特征的双子群果蝇优化算法[J]. 计算机应用,2015,35(5):1348-1352.

[19] RICHER T J, BLACKWELL R A. The Levy particle swarm[J].IEEE Congress on Evolutionary Computation,2006,7:808-815.

(编 辑 亢小玉)

Applying improved quantum behaved particle swarm optimization used for neural networks model to load forecasting

ZHANG Lan1,2

(1.School of Natural and Applied Sciences, Northwestern Polytechnical University, Xi′an 710129, China;2.Department of Basic, Xi′an Aeronautical Polytechnic Institute, Xi′an 710089， China)

An improved quantum particle swarm optimization algorithm based on Levy flight is proposed, which is applied to the training phase of the wavelet neural network. The flight strategy based on Levy distribution is adopted to expand the search space of particles, making it easy for the particle to escape from the local optimum. The improved quantum behaved particle swarm optimization free from some disadvantages of the conventional neural networks training process, such as being likely to run into local minimum points and slow convergence speed, enhances the generation ability of traditional neural network. Finally, the improved quantum behaved particle swarm optimization is used for the training of wavelet neural network of load forecasting model in the power system. The simulation results show that the proposed algorithm enjoys high forecasting precision.

Levy flight; quantum behaved particle swarm; neuron network; load forecasting

2015-05-11

国家自然科学基金资助项目(11471262);陕西省教育厅科研计划基金资助项目(15JK1381)

张兰，女，陕西西安人，博士生，从事优化算法研究。

TP183; TM 743

A

10.16152/j.cnki.xdxbzr.2016-05-004