针阀关闭时刻柴油机不同喷孔内流场的计算
2016-12-12文华李潜徐颖韬
文华, 李潜, 徐颖韬
(南昌大学机电工程学院, 江西 南昌 330031)
针阀关闭时刻柴油机不同喷孔内流场的计算
文华, 李潜, 徐颖韬
(南昌大学机电工程学院, 江西 南昌 330031)
基于开源软件OpenFOAM定义两种连续的网格运动使针阀完全关闭,分三步数值模拟针阀关闭时刻喷孔内的瞬态流场,模拟结果与S.Jollet试验结果基本吻合。在此基础上研究喷孔结构参数对孔内流场的影响,计算结果表明,随着孔径的增大,喷孔内残余燃油内部有气泡形成;喷孔长度越短,喷孔内残余燃油内部的空气体积越大,形成的气泡越靠近压力室;K系数的减小有利于喷孔内气泡的产生。
喷孔;数值模拟;流场;气泡
目前国内对柴油机喷孔内燃油流动的研究大多是关于针阀关闭前的瞬态流动,其流动特性也只局限于空穴现象,有关针阀关闭时刻(EOI)[1-2]孔内流动特性的报道却很少看见。当喷油间隔期很短时,EOI的孔内流动状况对下一次的喷射过程会有很大的影响,因此对这段时间孔内流动特性进行研究很有必要。
近来的一些燃油喷射试验发现了EOI孔内流动的新特性,如在喷油结束后,压力室以及喷孔区域会产生气泡[3-4],这些气泡在下一次喷射过程中的破裂势必会对孔内流动造成影响。Swantek[5]认为该部分气泡是外部空气在燃油的卷吸作用以及内外压差作用下倒流进入喷孔形成的。Battistoni[6]利用CONVERGE软件建立模型,对针阀关闭时刻孔内的瞬态流场进行数值模拟,计算结果与试验结果吻合较好,这为进行数值模拟提供了依据。然而此模拟方法认为喷孔出口流量为0时,针阀完全关闭。事实上此时针阀升程为5 μm,这会使模拟结果产生偏差。因此,本研究定义两种连续的网格运动使针阀完全关闭,并在此基础上研究喷孔结构对针阀关闭时刻柴油机孔内流场的影响。
1 运动网格处理方法
为保证数值计算的顺利进行,针阀与阀座之间必须有网格的存在,这就造成了针阀不能完全关闭。为此,定义两种连续的网格运动来使针阀完全关闭:针阀关闭初期,通过压缩网格来实现针阀的运动;当针阀升程减小到0.02 mm时,利用滑移网格使压力室正上方的针阀锥面继续向下移动,从而达到针阀全关的效果。该种方法通过设计三套连续的计算网格来实现(见图1)。
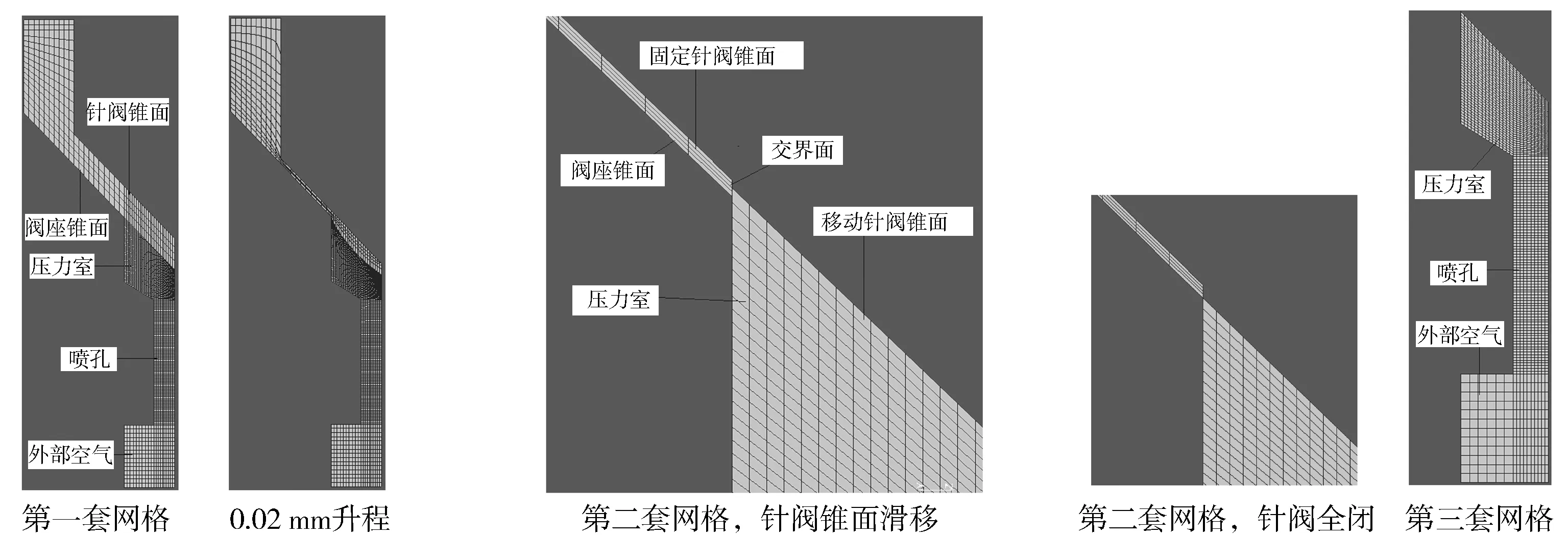
图1 运动网格处理方法
第一套网格以针阀全开(升程为0.3 mm)时的整个喷嘴为初始计算区域,通过网格的压缩实现针阀的运动,当针阀升程减小到0.02 mm时该部分网格运动结束。第二套网格以针阀升程为0.02 mm时的整个喷嘴为初始计算区域,将此时针阀密封锥面位置与压力室的交界面处理成滑移边界,同时将针阀锥面定义成两部分:阀座正上方的针阀锥面定义为固定壁面;压力室正上方的针阀锥面仍然定义为移动壁面。然后引入滑移网格,通过移动压力室正上方的针阀锥面向下运动使之压缩压力室部分的网格,造成针阀密封锥面位置与压力室相互滑移,使交界面面积减小。当相互滑移0.02 mm时,该交界面面积减为0,此时阀座上方的燃油不能经该交界面流入压力室,可以认为针阀完全关闭。为减少计算量,第三套网格只以压力室和喷孔为计算区域。
整个三步计算过程如下:首先,利用第一套计算网格算出针阀全开时整个喷嘴的稳态流场,接着以此流场为初始流场计算出针阀移动到0.02 mm升程时的流场;然后,采用第二套网格,利用软件中的流场映射功能,将上一步中0.02 mm升程时的流场映射过来作为初始流场并引入滑移网格计算出针阀全闭时压力室及喷孔内的流场;最后,采用第三套网格,同样应用流场映射功能,以第二步计算得出的流场作为初始值,计算针阀关闭时到下一次喷油前的流场。
2 计算模型的建立及验证
2.1 喷嘴内两相流动模型
基于VOF方法[7]引入动网格以及接触角[8]建立不可压缩两相流模型对针阀关闭时刻喷孔内流场进行瞬态模拟。
VOF方法的气体输运方程为
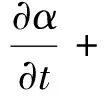
(1)
式中:α为在整个流场中一种流体体积与网格体积的比值。若α=0则表示该网格不含该流体,若α=1则表示该网格充满该流体,若0<α<1则表示该网格区域含有自由面。根据体积比函数α来追踪和构造自由面。
本研究忽略液相的蒸发,认为流动等温且不可压缩,考虑气液两相间的渗透及表面张力的影响,除对能量方程的求解外,建立两相混合流动的控制微分方程组:

(2)
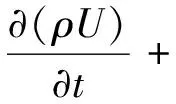
(3)
式中:ρ为混合密度;t为时间;U为速度;p为压力;τ为黏性切应力;σ为表面张力系数;κ为界面曲率;n为流体表面S的单位法相矢量;δ(x)为气液界面处的狄拉克函数。式(3)中等号最右边的积分项表示在液相表面,由于表面张力产生的求面积分的动量源项。
本研究采用均相流模型,认为气液两相是一种混合均匀相,混合相物性参数的值为各相的加权平均数。混合相密度ρ以及黏度μ通过式(4)和式(5)得出:
ρ=αρl+(1-α)ρg,
(4)
μ=αμl+(1-α)μg。
(5)
式中:α为液相体积分数,下角标l代表液相,g代表气相。
2.2 初始边界条件的设定
参照S.Jollet[9]实验的初始喷射条件,并减小网格依赖性[10]对计算结果的影响,通过对该实验中孔径为0.2 mm和0.4 mm的喷孔进行计算,验证计算模型的可靠性。
为减少计算量,取喷孔的一半作为计算对象,剖面设为对称边界,进出口设为压力边界,具体设定见表1,其他则均采用壁面边界。表2示出了柴油及空气的物性参数。

表1 两种喷孔压力边界条件的设定

表2 柴油及空气的物性参数
2.3 计算模型的验证及分析
图2示出S.Jollet实验中0.2 mm和0.4 mm孔径喷孔的试验与模拟结果对比。从图中可以发现,0.2 mm喷孔中没有气泡产生,而0.4 mm喷孔有气泡吸附在针阀锥面上。由于本次计算时间为针阀关闭后2 ms,当给定更多的计算时间时,喷孔内的气泡会在浮力作用下上升至压力室,故可以认为计算结果与试验结果吻合,验证了该模拟方法的可靠性。

图2 液相体积分数试验值与模拟值对比
3 计算结果及分析
3.1 针阀关闭时刻不同直径喷孔内的流场分布
保持喷孔长度为1.2 mm,分别对孔径为0.2,0.3,0.4 mm的喷孔进行计算。图3示出3种喷孔在针阀关闭后2 ms时孔内的液相体积分布图。可以看出,随着孔径的增大,孔内残余燃油内部成形的气泡从无到有。从图4可以看出,随着孔径的增大,喷孔内柴油残余率减小,而倒流进入燃油内部的空气体积增大,其中Vbubble能反映出气泡的体积,说明孔径的增加有利于气泡的形成。

图3 针阀关闭2 ms后喷孔的液相体积分数

图4 针阀关闭时喷孔内柴油残余率Pdiesel及残余柴油内部的空气体积Vbubble随孔径的变化
图5示出3种喷孔在针阀关闭时的速度矢量。可以看出, 0.2 mm喷孔孔内的速度方向基本是沿着喷孔中心轴线方向,随着孔径的增大,速度方向变得紊乱,速度值增大。这是因为孔径增加,喷孔对燃油流动的约束减弱。喷孔内速度方向越紊乱,空气越容易被卷入燃油内部形成气泡。
图6示出3种喷孔在针阀关闭时出口截面的流场分布。从液相图可以看出,针阀关闭时3种喷孔出口截面有一部分被空气占据,说明空气发生了倒流。随着孔径的增加,截面上气液两相的界面变得不规则,有利于燃油的卷吸作用。在沿喷孔中心轴线方向的分速度图中(沿出口方向为正,压力室方向为负,下同),空气相的速度基本是负方向,而燃油相则相反。随着孔径的增加,空气相的速度增加,说明空气的倒流作用加强,并且两相之间的速度差值也随之增加,加强了空气与燃油的相互作用,促进空气被卷入燃油内部。

图5 针阀关闭时3种喷孔的速度矢量
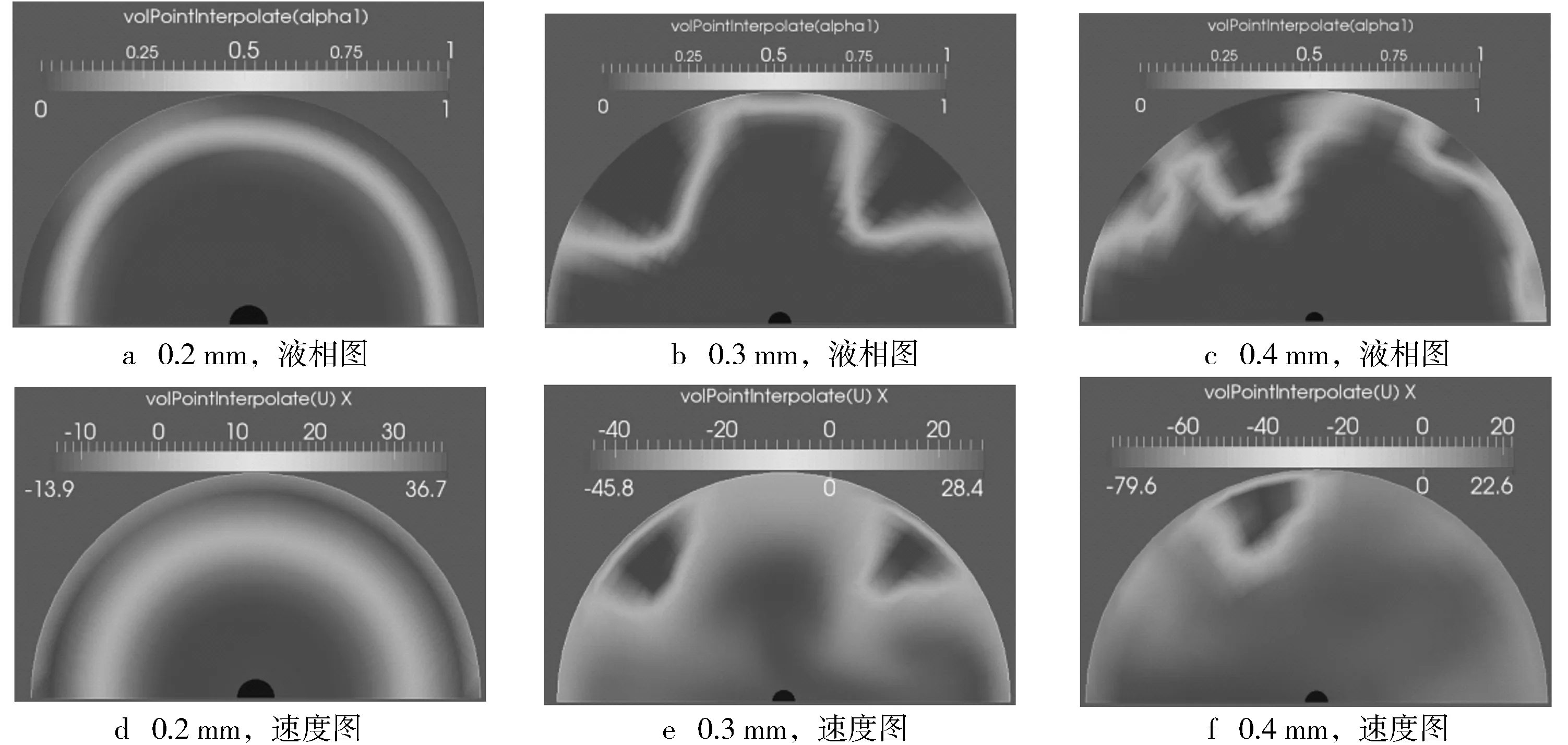
图6 针阀关闭时3种喷孔出口截面的流场分布
3.2 针阀关闭时刻不同长度喷孔内流场的分布
保持孔径为0.4 mm,对长度分别为0.6,0.9,1.2 mm的喷孔进行计算。图7示出3种喷孔在针阀关闭2 ms时的液相体积分布。显然,3种喷孔内都有大的气泡生成,并且随着孔径的缩短,气泡更靠近压力室。图8示出喷孔内柴油残余率和倒流进入燃油内部的空气体积随喷孔长度的变化关系。可以看出,喷孔长度变小,喷孔内残余燃油内部的气体体积增大,但有助于残余柴油的排出。

图7 针阀关闭后2 ms时3种喷孔的液相体积分布

图8 针阀关闭时喷孔内Pdiesel及Vbubble随喷孔长度的变化
图9示出3种喷孔在针阀关闭时出口截面的流场分布。随着喷孔长度的缩短,燃油在孔内流动的沿程损失减小,故其在出口截面的速度有增大的趋势。同上一节所述,此时气液两相在出口附近相互作用。并且随着喷孔长度的缩短,空气的速度增大,使得空气倒流作用加强,同时气液两相之间的速度差值增加,加剧了燃油的卷吸作用,其结果是更多的空气被卷入燃油内部形成气泡。

图9 针阀关闭时3种喷孔出口截面的流场分布
3.3 针阀关闭时刻不同K系数喷孔内流场的分布
对于锥形喷嘴,系数K定义为锥度系数,其公式为
K=100(din-dout)/H。
(6)
式中:din为喷孔的入口直径;dout为喷孔的出口直径;H为喷孔的长度。为保证各喷孔的出口流量相同,保持喷孔出口直径为0.4 mm不变。
保持喷孔长度为1.2 mm,对K系数分别为0,2.5,5的喷孔进行计算。从图10中可以看出,3种喷孔中都有成形的气泡,当K=0时,气泡体积最大。再对照图11,发现随着K系数增加,倒流进入燃油内部的空气体积有减小的趋势,而喷孔内残余柴油量有增大的趋势,说明K系数的减小对气泡的产生和残余燃油的排出有促进作用。

图10 针阀关闭后2 ms时3种喷孔的液相体积分布

图11 针阀关闭后2 ms时喷孔内Pdiesel及Vbubble随K系数的变化
从图12中可以看出,K系数减小,燃油相在出口截面的速度增大,有利于燃油的排出。K系数减小,气液两相之间的速度差值增加,同上两节所述,气液两相之间的相互作用得到加强,空气更容易被卷入燃油内部。
4 结论
a) 随着孔径的增大,喷孔内残余燃油内部有气泡形成,倒流进入残余燃油内部的空气体积也有增大的趋势;
b) 喷孔长度越短,喷孔内残余燃油内部的空气体积越大,形成的气泡越靠近压力室;
c) K系数越小,喷孔内的气泡体积越大。
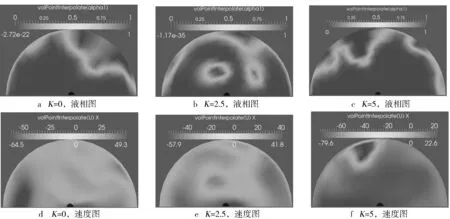
图12 针阀关闭时3种喷孔出口截面的流场分布
[1] Alan Kastengren. End-of-Injection Behavior of Diesel Sprays Measured With X-Ray Radiography[J]. J. Eng. Gas Turbines Power,2012,134(9):279-287.
[2] Musculus. Entrainment Waves in Diesel Jets[J].SAE Int. J. Engines,2009,2(1):1170-1193.
[3] 彭天鹏.喷油嘴内部流动及近场喷雾结构的试验与数值模拟研究[D].南昌:南昌大学,2010.
[4] 姜光军,张煜盛,Medhat Elkelawy,等.不同燃料的喷嘴内流动与喷雾形态可视化试验[J].农业机械学报,2014,45(5):22-29.
[5] Swantek A B,Duke D,Tilocco F Z,et al. End of Injection, Mass Expulsion Behaviors in Single Hole Diesel Fuel Injectors[C]//ILASS Americas 26th Annual Conference on Liquid Atomization and Spray Systems.Portland:[s.n.],2014.
[6] Battistoni M,Kastengren A L,Powell C F,et al. Fluid Dynamics Modeling of End-of-Injection Process[C]//ILASS Americas 26th Annual Conference on Liquid Atomization and Spray Systems.Portland:[s.n.],2014.
[7] 林宇星.基于VOF方法的喷嘴空穴流动与近场喷雾数值模拟研究[D].南昌:南昌大学,2013.
[8] Chen Fang. 3-D numerical simulation of contact angle hysteresis for microscale two phase flow[J].International Journal of Multiphase Flow,2008(34):690-705.
[9] Jollet S. Comparison of experiments and numerical simulations of high pressure transparent injection nozzles[C]//ILASS-Europe 2013, 25th European Conference on Liquid Atomization and Spray Systems.Chania:[s.n.],2013.
[10] 贾明,解茂昭,刘红,等.伞喷喷嘴内空化现象的数值模拟[J].内燃机学报,2011,29(3):213-220.
[编辑: 潘丽丽]
Calculation of Internal Flow Field in Different Nozzle Orifices of Diesel Engine at Needle Value Close Timing
WEN Hua, LI Qian, XU Yingtao
(College of Mechanical and Electrical Engineering, Nanchang University, Nanchang 330031, China)
A new algorithm consisting of two kinds of continuous mesh-moving was proposed to make the needle close completely based on the open source software Open FOAM and the transient internal flow field in nozzles was numerically simulated by three steps. The simulation results coincided with the experimental results of S.Jollet. The effects of nozzle structure parameters on the flow field inside the hole were further studied. The results show that the bubble in residual fuel of nozzle occurs with the increase of nozzle diameter. The shorter nozzle orifice length leads to larger bubble volume inside residual fuel and closer distance of bubble with pressure chamber. Besides, the decrease of K-factor is beneficial to the formation of bubbles.
nozzle orifice; numerical simulation; flow field; bubble
2015-09-17;
2015-12-14
国家自然科学基金项目(51466009)
文华(1976—),男,副教授,博士,研究方向为柴油机喷嘴燃油喷射;1725178115@qq.com。
10.3969/j.issn.1001-2222.2016.01.008
TK422
B
1001-2222(2016)01-0042-06
