封闭图形“内部”与“外部”的辨别探究

洪伟++郜舒竹

【摘 要】判断某点是处于一个闭合图形的内部还是外部，看起来是一个很简单的问题，但在一定条件下也会变得非常复杂。“内部还是外部”的学习活动即是让学生通过实践操作探索如何用数学方法解决该问题，发现规律，总结方法。学生将在知识技能、情感体验、数学思维、个性品质与社会性等多方面得到提升。

【关键词】封闭图形 内部 外部 规律

“内部还是外部”这个学习活动即是将一段细线打结形成闭合线圈，通过改变线圈的形状形成几个不同的闭合曲线图形，探索如何更便捷、准确地判断一枚一角硬币处于这几个曲线图形的内部还是外部的方法。

通过该学习活动学生会发现，原本一些感觉上非常简单、司空见惯或者显而易见的概念在一定条件下也会变得模糊不清、难以界定，也需要认真研究和探索。对于一些基本图形来说内部和外部可以一眼看出，很好判断，如长方形、三角形、梯形等，因此人们往往忽略对这种看似平常概念的深入探究和思考。活动提供一次范例引起学生对这些平常概念的关注和思考，适合小学五年级教学。

在该学习活动中学生将完整经历发现问题、探索问题、提出假设、验证假设、解决问题的全过程，并经历从简单到复杂再回到简单后又复杂化的情感体验。学生将体会到数学问题的模型化可以将具体的实际问题抽象成数学问题并使其得以简单清晰地解决，体会到数学的实用性和数学证明的严谨性。活动中展现出来的简单与复杂之间的反差及相互转化对学生思维具有很好的启迪作用。

活动中学生需要小组分工合作，组员分别轮流承担出题人、解题人和协助者的角色，并协作完成活动任务。学生的表达能力、沟通能力、分工协作能力和实践操作能力都将得到锻炼。

一、问题与动机

探讨一个点处于一个几何图形的内部还是外部看起来是一个非常简单的问题，但如果这个几何图形是一个闭合的曲线图形，问题还是不是那么简单呢？如果这个曲线图形非常复杂，如何更有效、更快捷地判断出哪是内部哪是外部呢？

提出问题、引发思考这一环节需要教师把握课堂节奏、营造适宜气氛，生动地展现问题的简单与复杂之间的反差，引发学生的兴趣和探索欲。教师分三步展示图1、图2、图3，每次询问学生图中的一角硬币处于图形的内部还是外部。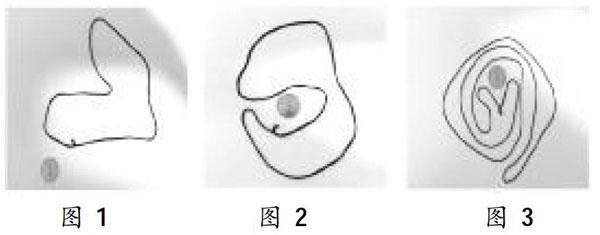

展示图1和图2时学生一般会认为问题实在是太简单了，然后教师给出图3，展示反差，并询问如果图形再复杂一些，用观察法判断不出来，怎么办。抛出疑问，引发接下来的探索活动。

活动的主要内容是引导学生通过对几个不同闭合曲线图形内部外部的判断，探索总结规律，建立简单数学模型。需要准备的学习用具包括：一段1米长的细绳、一枚一角硬币、一枚五角硬币、一把30厘米长的直尺。

二、过程与设计

感知到从简单到复杂的反差后，教师可以给学生一小段自由讨论和思考的时间。学生可以先进行天马行空的想象，因为与书本上学过的知识看起来关系不大，学生受到的束缚和思维定势的影响较小，利于发散性思维的培养。通常情况下经过讨论后学生会给出一些直观的办法，例如直接观察，把曲线图形看成迷宫、硬币看成小虫子尝试能不能找到出路，把曲线图形进行适当的变形处理再观察判断，等等。将该问题与数学知识关联起来总结归纳出一般化解决方法的概率较小。学生自己有了一定的思考后，教师再介绍本活动的探索步骤，更有利于其体会数学在解决实际问题中的作用。

教师将学习用具分发给学生，并介绍活动步骤如下：

1.所有学生分成3～4人的小组，组员之间自行商量分工事宜，选出组长、发言人、记录员等角色。

2.取出细绳，并将两端系成一个结，形成一个闭合线圈。

3.将闭合线圈平放在桌面上，并将两枚硬币放在线圈的外部，注意使两枚硬币间的距离不超过30厘米（即直尺的长度）。

4.一名同学操作线圈，改变它的形状，使其围绕一角硬币形成一个较为复杂的闭合图形。注意线圈不能离开桌面，以保证两枚硬币始终处于线圈的外部。然后用直尺将两枚硬币连接起来，观察直尺所在的连接线段穿过线圈有几个交点，将结果记录在如下表 1所示的活动记录单中。每位同学轮流操作一次，注意使每次的线圈形状尽可能不同。教师可以先示范操作一次，学生有问题先提出解决，再小组展开活动。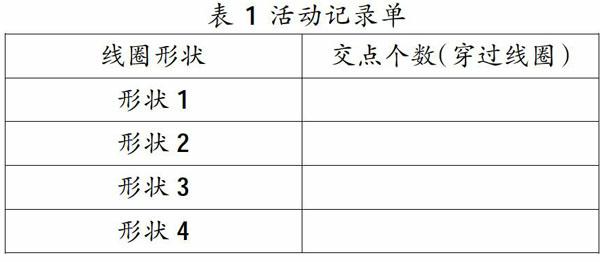

5.活动结束后，小组内先讨论记录下的交点个数有什么规律，试着总结规律，提出判断硬币处于曲线图形内部还是外部的方法。

三、规律与建模

小组活动结束后，每组的发言人上台讲解自己小组的发现与结论，教师组织全班展开讨论，使结论尽可能完善并引导学生用数学语言表达结论使之模型化。例如，用模型化的语言可以概括成：“要判断曲线图形上一点A处于图形的内部还是外部，可以在图形外建立另一点B，连接A和B形成线段AB，线段AB穿过曲线图形的交点个数记为n。当n为偶数时，点A处于曲线图形的外部。”模型的建立使具体的实际问题变成抽象的数学问题，复杂的问题又回归简单。

四、总结与反思

活动中学生经历的思维过程包括：实践操作、发现规律、归纳推理、模型化表达。规律指的是运动或变化过程中的不变因素。[1]活动中曲线图形和交点个数都是变化的，交点个数的奇偶性与内外部之间的对应关系是其中的不变因素。

从发现规律到提出结论运用的数学思维是归纳推理。从逻辑的角度说，归纳（induction）推理指的是人依据自身的意愿、经验和当前感知，从事实（fact）到推论（inference）的思维方式。[2]从有限个曲线图形中总结出的规律是经验和当前感知，用于判断内部还是外部的一般化方法是推论。由于曲线图形的种类和个数都是无穷多个，这里用的是不完全归纳，因此结论是否正确存在着不确定性。教师可以根据课堂情况引导学生质疑结论，引发其课后进行进一步的探索和思考。于是简单的结论如果想要严密的证明又似乎变得复杂了。整个探索过程学生体验到数学问题在简单和复杂间不断地奇妙变化，收获丰富的情感体验。

最后全班讨论环节使得结论得以模型化表达，学生可以体会到数学符号的简洁高效和数学语言的严谨性。

五、关联与拓展

开展该学习活动所需的用具很简单，学生课后可以自己准备用具继续探索两个问题：第一，当n为奇数时，点A是否处于曲线图形内部，改变曲线图形的形状多次验证并填写活动记录单；第二，尝试寻找反例。

教师可以引入数学史上类似运用不完全归纳法提出的著名数学问题，如哥德巴赫猜想等，引导有兴趣的同学进一步查阅相关资料拓展研究，思考有什么方法可以严密地证明课上提出的数学模型正确与否。

参考文献：

[1]郜舒竹.“探索规律”释义[J].课程·教材·教法，2015（1）.

[2]郜舒竹.小学数学这样教[M].上海：华东师范大学出版社，2015：137.

（首都师范大学初等教育学院 100048）