再谈数形结合在初中数学中的应用

张为安 黄生洪

（湖北省潜江市王场中学 湖北潜江 433100）

再谈数形结合在初中数学中的应用

张为安 黄生洪

（湖北省潜江市王场中学 湖北潜江 433100）

著名数学家华罗庚曾指出：“数与形，本是相倚依，焉能分作两边飞，数缺形时少直观，形当数时难入微；数形结合百般好，割裂分家万事非。”波利亚也说，掌握数学就意味着要善于解题，数学思想方法是灵魂和精髓，是知识转化为能力的桥梁，是解题过程中劈山开路的宝剑，所以在解决数学问题时，将抽象的数学语言同直观的图形相结合，实现抽象的概念与具体形象的联系和转化，使数与形的信息相互渗透，可以拓展解题思路，使数学问题简单化，明朗化。

下面举例说明数形结合在解决实际问题中的妙用：

一、利用数轴求不等式中取值范围

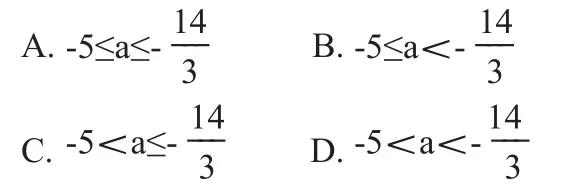
二、利用函数图像解决方程的近似解或解的个数问题

例2.设方程|x2-1|=k+1，试讨论k取不同范围的值时其不同解的个数的情况。

分析：我们可以把这个问题转化为确定函数y1=|x2-1|与y2=k+1的图像交点个数的情况，因函数y2表示平行x轴的所有直线，从图像可以直观的看出：

①当klt;-1时，y1与y2没有交点，这时原方程无解

②当k=-1时，y1与y2有两个交点，原方程有两个不同的解

③当-1lt;klt;0时，y1与y2有四个不同的解，原方程不同解的个数有四个

④当k=0时，y1与y2有三个交点，原方程不同解的个数有三个；

⑤当kgt;0时，y1与y2有两个交点，原方程不同解的个数有两个

三、利用数轴或坐标求最大值（或最小值）

例3.（1）如图，在直线l的同侧有A，B两点，在直线l上找到点P、P′，使PA+PB最小，|BP′-AP′|最大；

（2）平面直角坐标系内有两点A（2，3），B（4，5），请分别在x轴，y轴上找两点P、P′，使PA+PB最小，|BP′-AP′|最大，则P、P′的坐标分别是____

（4）在直角坐标系中有四点A（-8，3），B（-4，5），C（0，n），D（m，0），当四边形ABCD周长最短时，

分析：这是一组形异实同的题目，转化是解决这类问题的核心，而其基础知识就是运用两点之间线段最短在不同场合有简单到复杂的运用

（1）作A点关于直线l的对称点A′，连接A′B交直线l于点P，延长BA交l于点P′，则点P，P′为所求。

（2）点A关于x轴的对称点A′（2，-3），直线A′B的解析式为y=4x-11，y=0时，，所以点

直线AB的解析式为y=x+1，与y轴的交点为（0，1）所以P′（0，1）

（3）①

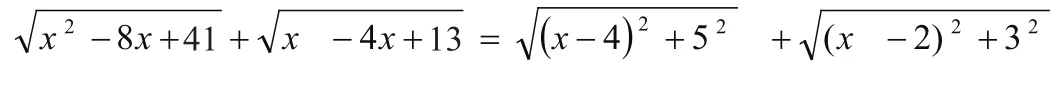
②类似于（1），延长BA交x轴于P′，则

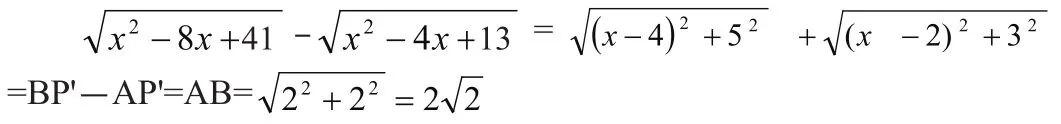
（3）作点B关于y轴的对称点B′，作点A关于y轴的对称点A′，则点B′（4，5），A′（-8，-3），则A′B′的解析式为

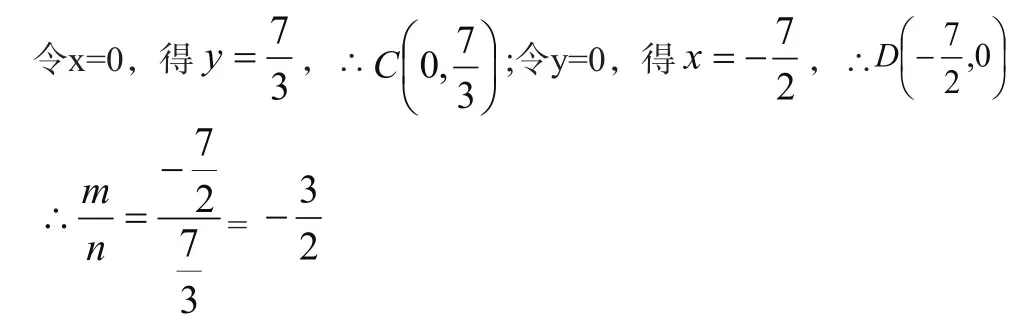
结束语

数形结合既具有数学学科的鲜明特点，又是数学研究中的常用方法，数形结合是解决具体问题的宝剑，是寻求出路的突破口，数形结合最大的特点就是模式化，直观化，用简单直观的图形代替繁琐的代数推理，数形结合是数学中的基本而又重要的思想，可见数与形珠联璧合，相映生辉。