Acoustomechanics of semicrystalline polymers

Fengxian Xin∗,Tianjian Lu

aState Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University,Xi’an 710049,China

bSchool of Engineering and Applied Sciences,Harvard University,MA 02138,USA

cMOE Key Laboratory for Multifunctional Materials and Structures,Xi’an Jiaotong University,Xi’an 710049,China

Letter

Acoustomechanics of semicrystalline polymers

Fengxian Xina,b,c,∗,Tianjian Lua,c

aState Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University,Xi’an 710049,China

bSchool of Engineering and Applied Sciences,Harvard University,MA 02138,USA

cMOE Key Laboratory for Multifunctional Materials and Structures,Xi’an Jiaotong University,Xi’an 710049,China

H I G H L I G H T S

•An acoustomechanical theory for semicrystalline polymers is established.

•We demonstrate that acoustic radiation force is capable of causing giant deformation in these materials.

•We demonstrate that pull-in instability can be acoustically triggered even if the in-plane mechanical force is fixed.

•The findings of this study enable reliability design of novel acoustic actuated devices.

A R T I C L EI N F O

Article history:

28 December 2015

Accepted 31 December 2015

Available online 25 January 2016

Acoustomechanics

Semicrystalline polymers

Instability

Bifurcation

We develop an acoustomechanical theory for semicrystalline polymers and demonstrate that acoustic radiation force is capable of causing giant deformation in these materials.When a polymer layer is subjected to combined tensile mechanical force in plane and acoustic force(sound pressure)through thickness,it becomes initially homogeneously thin but soon inhomogeneous when the two forces reach criticalconditions.Criticalconditionsforsuchacoustomechanicalinstabilityaretheoreticallydetermined based on the J2-deformation theory.We demonstrate that pull-in instability can be acoustically triggered even if the in-plane mechanical force is fixed.Bifurcation in the critical condition for acoustomechanical instabilityoccurswhenthepolymerexhibitssufficientlylargehardening.Thefindingsofthisstudyenable reliability design of novel acoustic actuated devices.

©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

Semicrystalline polymers are extensively applied in electromechanical devices,due to their superior performance on large mechanical actuation induced by external stimuli such as electric/magnetic field,temperature,and mechanical stress[1–3]. For such applications,failures like necking and pull-in instability should be avoided,since excessive thinning down of polymer filmsoftenhappenswhenactuatedbyexternalstimuli.Asprevious studies mainly focused upon electrical actuation and electromechanical instability of semicrystalline polymers,there is a basic lack of understanding of their acoustic actuation and acoustomechanical instability.Innovative design of acoustic actuated devices urgently calls for theoretical guideline on acoustomechanical behavior of semicrystalline polymers.

Thispaperaimstoinvestigatetheacousticactuationandacoustomechanical instability of semicrystalline polymers subjected to combined mechanical force and ultrasound pressure.The focus is placed upon critical conditions for mechanically induced necking instability at prescribed acoustic inputs and acoustically induced pull-in instability at prescribed mechanical forces.

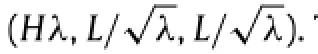
As the propagation of ultrasound wave in a semicrystalline polymer is accompanied by acoustical momentum transfer between adjacent medium particles,a steady time-averaged acousticradiation stress is generated along wave propagation path in the medium,which can be expressed as[4–8]

http://dx.doi.org/10.1016/j.taml.2015.12.004

2095-0349/©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

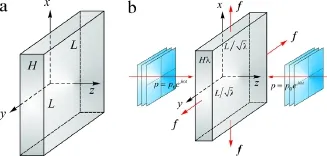
Fig.1.(Color online)(a)A thin layer of semicrystalline polymer in undeformed state with dimensions(H,L,L);(b)deformation of polymer under aco ustic loads and equal biaxial mechanical forces in current state with dimensions

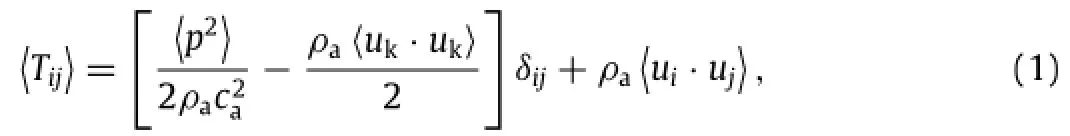
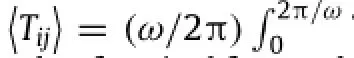
Accounting for both the nonlinear elastic behavior of semicrystalline polymers and acoustic radiation stress,we write the Cauchy stress in the material as

where FiK=∂xi/∂XKis the deformation gradient and W(F) the Helmholtz free energy function.We adopt the J2-deformation theory[13]to consider the nonlinear deformation,obtaining thence W(F)=K(lnλ)N+1/(N+1)for which the parameters Kand N can be obtained from experimental stress versus strain curves.K scales with polymer yield strength,thus much smaller than polymer elastic modulus.N describes polymer strainhardening.N=K=1 corresponds to linear elasticity while N=0 corresponds to ideal plasticity.For semicrystalline polymers,N typically varies between 0.1 and 0.6[14,15].

Since the semicrystalline polymer is taken as nearly incompressible,its deformation state under equal biaxial forces and acoustic inputs will remain almost unchanged if a hydrostatic stress is superimposed.Therefore,the deformation state under the combined loads is approximately equivalent to that under uniaxial compressive stressing,as illustrated in Fig.2.Following the J2-deformation theory,the true logarithmic strain is expressed as ε=lnλwhen extension andε= −lnλwhen compression. Therefore,nonlinear large deformation ofthe semicrystalline polymer can be described as

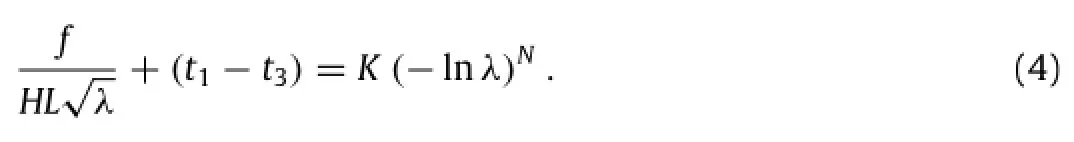
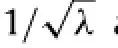
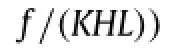
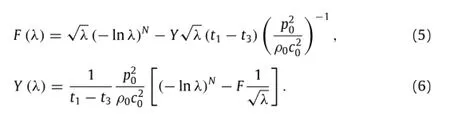
Eq.(5)specifies the dependence of F onλat prescribed acoustic input while Eq.(6)specifies the dependence of Y onλat prescribed mechanical force.

Variations of F and Y withλare presented separately in Fig.3(a)and(b),the former at fixed acoustic force and the latter at fixed mechanical force.Overall,the variation trends of these force–stretch curves stem from the competition between material hardening and geometric nonlinearity.In small deformation regime(λ≈1),material hardening dominates,causing both curves to increase monotonically.In large deformation regime (λ≪ 1),geometric nonlinearity dominates,causing the curves to decease,during which the softening effect offsets the material hardening effect.Competition of the two counteracting effects induces a peak on each force–stretch curve,thus giving rise to the critical condition for acoustomechanical instability to occur. Peaks in Fig.3(a)correspond to necking instabilities caused by mechanical tensile force at fixed acoustic forces,whereas peaks in Fig.3(b)correspond to pull-in instabilities caused by acoustic compressive force at fixed mechanical forces.As the prescribed acoustic force is increased,the critical mechanical force deceases but the critical stretch increases(Fig.3(a)).In contrast,both the criticalacoustic force and criticalstretch decrease as the prescribed mechanical force is increased(Fig.3(b)).

As acoustomechanical instability occurs when the incremental stiffness turns from positive to negative,we can determine the critical condition by setting∂F(λ)/∂λ=0 at fixed Y or∂Y(λ)/∂λ=0 at fixed F.For the problem of Fig.1,the critical condition of mechanical force–stretch relation is

and the critical condition of acoustic force–stretch relation is

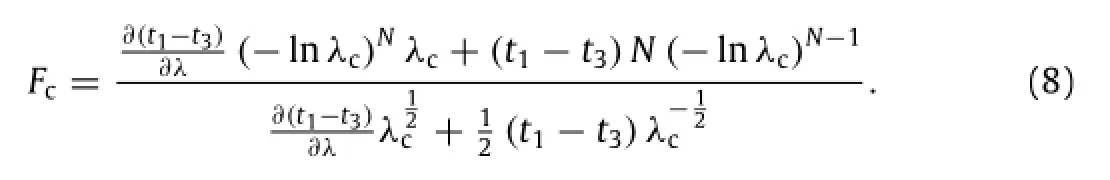
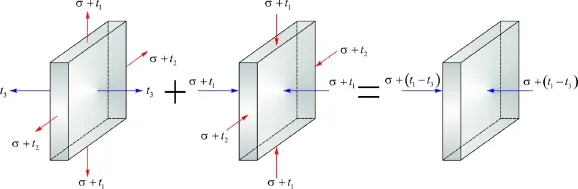
Fig.2.(Color online)Strain state of a nearly incompressible polymer under acoustic radiation forces and equal biaxial forces is equivalent to that induced by uniaxial compressive stressσ+(t1−t3).

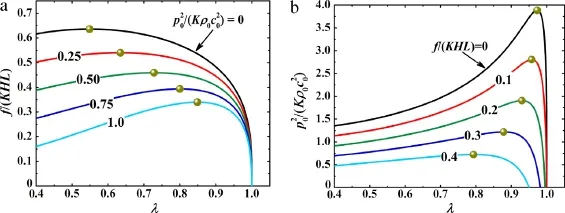
Fig.3.(Color online)(a)Normalized mechanical force plotted as a function of stretch for selected acoustic inputs;(b)normalized acoustic input plotted as a function of stretch for selected mechanical forces.

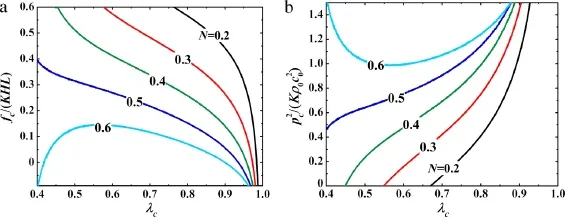
Fig.4.(Color online)(a)Critical mechanical force and(b)critical acoustic input plotted as functions of critical stretch for selected hardening exponents.

Eqs.(7)and(8)generalize the critical condition of necking instability induced by tensile mechanical force andthe critical condition of pull-in instability induced by compressive acoustic force.Figure 4(a)and(b)plots the critical mechanical and acoustic forces as functions of critical stretchλcfor selected values of material hardening exponent N.For a givenλc,the critical mechanical force decreases while the critical acoustic force increases with increasing N.When N is large enough(such as 0.6 considered here),bifurcation occurs in the critical condition because two possible critical stretches are associated with one given critical force.Although only tensile mechanical force has beenconsideredinthepresentstudyforbrevity,theresultsofFig.4 can be extended to compressive mechanical force as long as the polymer does not buckle.The compressive force will increase the critical acoustic force whenλc＞1.

We analyze further the critical condition of acoustomechanical instability by using the relationship between critical mechanical and acoustic forces(Fig.5).Overall,increasing the hardening exponent N results in reduced critical forces.Bifurcation occurs in the critical force phase diagram when N=0.6 as shown in Fig.5. This bifurcation phenomenon is attributed to the quasi-periodicity of acoustic force as a function of through-thickness stretch.

In summary,we present critical conditions for the occurrenceofacoustomechanicalinstabilityinsemicrystallinepolymers subjected to combined mechanical and acoustic forces.The J2-deformation theory is adopted to describe the nonlinear constitutive behavior of polymer.We demonstrate that acoustic force can cause giant deformation of semicrystalline polymers having mega Pascal elastic moduli.We also demonstrate that pull-in instability of polymer can be acoustically triggered at fixed mechanical force. Bifurcation occurs in the critical condition of acoustomechanical instabilitywhenthepolymerexhibitssufficientlylargestrainhardening.The acoustomechanical theory can be extended to consider other types of soft matters and the obtained conclusions are gen-erally true when adopting other material laws.This work presents promising applications of acoustic actuated devices and provides useful guideline for reliability design of these devices.

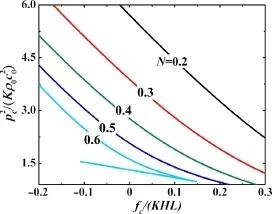
Fig.5.(Color online)Critical conditions for the occurrence of acoustomechanical instability:critical mechanical force plotted as a function of critical acoustic force for selected hardening exponents.

Acknowledgments

This work was supported by the National Natural Science Foundation of China(51528501 and 11321062)and the Fundamental Research Funds for Central Universities(2014qngz12).Xin is supportedbyChinaScholarshipCouncilasavisitingscholartoHarvard University.This author appreciates the helpful discussions with Prof.Zhigang SuoandDr.RuobingBaiat HarvardUniversity on soft material theory.

References

[1]Q.M.Zhang,V.Bharti,X.Zhao,Giant electrostriction and relaxor ferroelectric behavior in electron-irradiated poly(vinylidene fluoride-trifluoroethylene) copolymer,Science 280(1998)2101–2104.

[2]K.H.Stark,C.G.Garton,Electric strength of irradiated polythene,Nature 176 (1955)1225–1226.

[3]Q.M.Zhang,H.Li,M.Poh,et al.,An all-organic composite actuator material with a high dielectric constant,Nature 419(2002)284–287.

[4]L.V.King,On the acoustic radiation pressure on spheres,Proc.R.Soc.A 147 (1934)212–240.

[5]R.T.Beyer,Radiation pressure—the history of a mislabeled tensor,J.Acoust. Soc.Am.63(1978)1025–1030.

[6]R.T.Beyer,Radiation pressure in a sound wave,Amer.J.Phys.18(1950)25–29.

[7]A.A.Doinikov,Acoustic radiation pressure on a compressible sphere in a viscous fluid,J.Fluid Mech.267(1994)1–22.

[8]F.X.Xin,T.J.Lu,Acoustomechanical constitutive theory of soft materials,J. Mech.Phys.Solids(2015)submitted.

[9]X.Zhao,Q.Wang,Harnessing large deformation and instabilities of soft dielectrics:Theory,experiment,and application,Appl.Phys.Rev.1(2014) 021304.

[10]P.Mishra,M.Hill,P.Glynne-Jones,Deformation of red blood cells using acoustic radiation forces,Biomicrofluidics 8(2014)034109.

[11]B.Issenmann,A.Nicolas,R.Wunenburger,et al.,Deformation of acoustically transparent fluid interfaces by the acoustic radiation pressure,Europhys.Lett. 83(2008)34002.

[12]K.Thimmavajjula Narasimha,E.Kannan,K.Balasubramaniam,Simplified experimental technique to extract the acoustic radiation induced static strain in solids,Appl.Phys.Lett.91(2007)134103.

[13]J.Hutchinson,K.Neale,Proceedings of the IUTAM Symposium on Finite Elasticity,Springer,1982,pp.237–247.

[14]X.Zhou,X.Zhao,Z.Suo,et al.,Electrical breakdown and ultrahigh electrical energy density in poly(vinylidene fluoride-hexafluoropropylene)copolymer, Appl.Phys.Lett.94(2009)162901.

[15]X.Zhao,Z.Suo,Electromechanical instability in semicrystalline polymers, Appl.Phys.Lett.95(2009)031904.

25 December 2015

in revised form

∗at:State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University,Xi’an 710049,China.

E-mail addresses:fengxian.xin@gmail.com(F.X.Xin),tjlu@mail.xjtu.edu.cn (T.J.Lu).

*This article belongs to the Biomechanics and Interdiscipline