Adhesion-governed buckling of thin-film electronics on soft tissues

Bo Wang,Shuodao Wang

School of Mechanical and Aerospace Engineering,Oklahoma State University,Stillwater,OK,74078,USA

Letter

Adhesion-governed buckling of thin-film electronics on soft tissues

Bo Wang,Shuodao Wang∗

School of Mechanical and Aerospace Engineering,Oklahoma State University,Stillwater,OK,74078,USA

H I G H L I G H T S

•Adhesion-governed buckling physics for thin-film on elastomer.

•The transitions between buckling modes are predicted analytically.

•Mechanics discussed in the context of bio-integrated electronics applications.

A R T I C L EI N F O

Article history:

Accepted 20 November 2015

Available online 24 December 2015

Stretchable electronics

Bio-electronics

Buckling

Work of adhesion

Bio-interface

Stretchable/flexible electronics has attracted great interest and attention due to its potentially broad applications in bio-compatible systems.One class of these ultra-thin electronic systems has found promising and importantutilities in bio-integrated monitoring and therapeutic devices.These devices can conform to the surfaces of soft bio-tissues such as the epidermis,the epicardium,and the brain to provide portable healthcare functionalities.Upon contractions of the soft tissues,the electronics undergoes compression and buckles into various modes,depending on the stiffness of the tissue and the strength of the interfacial adhesion.These buckling modes result in different kinds of interfacial delamination and shapes of the deformed electronics,which are very important to the proper functioning of the bioelectronic devices.In this paper,detailed buckling mechanics ofthese thin-film electronics on elastomeric substrates is studied.The analytical results,validated by experiments,provide a very convenient tool for predicting peak strain in the electronics and the intactness of the interface under various conditions.

Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/ 4.0/).

Stretchable electronics,being as stretchable and flexible as soft tissues,has enabled many important applications,such as[1–8] eyeball-like digital cameras[9,10],sensitive robotic skins[11,12], smart surgical gloves[13],comfortable skin sensor[14],and structural health monitoring devices[15].Among these applications, some of the most important ones are the bio-integrated monitoring and therapeutic devices that can conform to the surfaces of soft bio-tissues such as the epidermis[16],the epicardium[17], and the brain[18],which provide promising options for longtermand portable healthcare devices.Upon contractions ofthe soft tissues,the electronics undergoes compression and buckles into various modes[19,20].A few important mechanics models were developed to study the buckling problems on similar film-onelastomer systems.Jiang et al.[2]studied the buckling behavior of strongly-bonded film-on-elastomer structures and predicted the maximum strain in the thin film to prevent fracture.Wang et al.[1] described local and global buckling modes for one-dimensional thin films or two-dimensional thin membranes on elastomers,and obtained the analytical critical conditions for separating the two buckling modes.Cheng etal.[21]introduced a bi-layer elastomeric substrate(a soft layer laminated on top ofa relatively stiffone)that yields high levels of stretchability,and discussed the buckling and post-buckling behaviors.To achieve optimum bio-compatibility, Ko et al.[22]and Wang et al.[23]introduced advanced strategies to wrap thin-filmelectronics onto arbitrarily curvilinearshapes,for which Wang et al.[23]developed an analytical model to study the buckling patterns,and showed thatthe buckling behaviors are governed by the strength of the interface and the level of the compressive strain.

These important mechanics models indicate that the buckling behavior of these film-on-elastomer structures is related to the applied strain,the material and geometric parameters of the film, the stiffness of the elastomer,as well as the strength of the interfacial adhesion.In the context of bio-electronics applications where the tissues are the elastomeric substrate,the stiffness of the tissues and the strength of the interface can vary in a very wide range due to the type of tissues and changes in temperature, moisture,and bio-chemical activities.The intactness of the interface is of great importance to the functioning of electronic devicesthat rely on intimate contact and coupling to the tissues.Detailed mechanics analysis of the buckling physics that accounts for any tissue stiffness and any interfacial adhesion is presented in this study to predict the intactness of the bio-electronics interfaces.

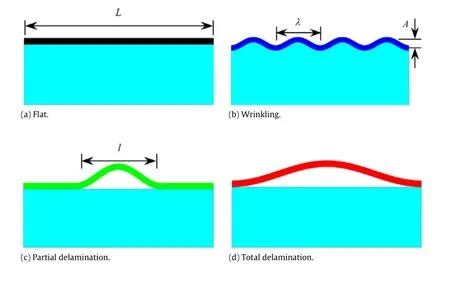
Fig.1.The four buckling modes:(a)flat;(b)wrinkling;(c)partial delamination;(d)total delamination.

The various buckling modes in the previous work[1,2,16–20] can be categorized into the four modes shown in Fig.1.Under none to minor compression,the film does not buckle and remains flat(Fig.1(a));as the compression increases,the film wrinkles into multiple small waves on top of the elastomer but does not delaminate from the interface,which we refer to as the wrinkling mode(Fig.1(b));under further compression,the multiple waves merge into one and cause the film to partially delaminate from the interface,which is the partial delamination mode(Fig.1(c)); more compression eventually causes the film to delaminate totally from the interface,which we define as the total delamination mode in this study(Fig.1(d)).The energies of these different buckling modes are formulated and then compared in the next section to explain transitions between them.

Here we consider a film-structure of length L,thickness h,and Young’s modulus E laminated on top of a soft substrate of Young’s modulus Es,and the work of adhesion for the interface isγ,and the structure is under a compressive applied strain of|ε|.By assuming a sinusoidal buckling shape of wavelength 0＜ l＜ L (Fig.1(c)),Wang et al.[23]analyzed the energies for the flat,partial and total delamination modes.Their analysis is elaborated in the Supplementary Information and summarized in the following.All the energies are normalized byfor convenience, whereWe also define the following non-

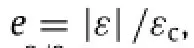
For the flat mode,the total energy of the system consists of the membraneenergyofthefilm,andtheadhesionenergyoftheentire interface,and is obtained as

For the partial delamination mode,the total energy consists of the membrane and bending energy of the film and the adhesion energyoftheun-delaminatedpartoftheinterface[lengthof(L−l)], and is obtained as

Energy minimization with respect to a requires the first derivative of Eq.(2)to be zero and the second derivative to be greater than zero,therefore a can be solved from

where a≤1 is due to the constraint that l≤L.

For the total delamination mode,the energy consists of the membrane and bending energy of the film,and is obtained as

In this study,we find that a fourth buckling mode,i.e.the wrinkling mode,exists under certain conditions.Following similar approach of Jiang et al.[2],the energy of this mode consists of the membrane and bending energies of the film,the strain energy of the substrate,as well as the adhesion energy of the interface,and can be obtained analytically as strain exceeds the critical buckling strain,namely e＞ew.

Here we adopt a typical case of ew=4 and g=3 to facilitate the discussion.Figure 2 shows the four energy curves versus the normalized strain e.All the curves are obtained analytically from Eqs.(1)to(5),except for the case of local buckling(blue curve).It is clearlyshowninFig.2thatforverysmallstraine,theflatmodehas the lowest energy.As e increases,wrinkling,partial delamination and then total delamination modes become the lowest energy state in sequence.Intersections of the above energy curves are important because they indicate the transitions from one buckling mode to another.Depending on the values of ewand g,there are 6 possible intersections between these curves,which are found below.

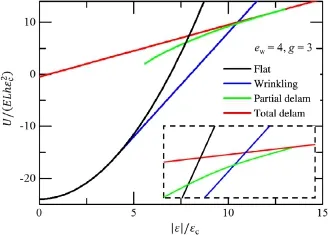
Fig.2.Normalized energy curves of the four buckling modes versus normalized applied strain.The inset in the dashed box shows illustrative details of the intersection points(not to scale)between the four curves.(For interpretation of the references to color in this figure legend,the reader is referred to the web version of this article.)

The intersection between flat and wrinkling(black and green curves)is found by setting(Eqs.(1)and(5)),which yields

The intersection between flat and total delamination(black and red curves)is found by setting(Eqs.(1)and(4)), which yields

The intersection between wrinkling and total delamination (black and red curves)is found by setting(Eqs. (4)and(5)),which yields

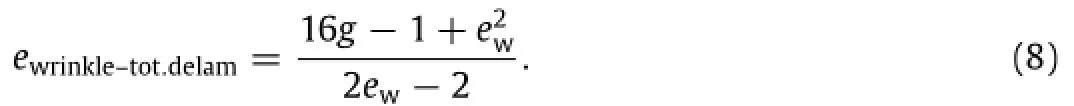
Following the analysis of Wang et al.[23],the intersection between flat and partial delamination is found to be

and that between partial delamination and total delamination is

The intersection between wrinkling and partial delamination cannot be obtained analytically because the energy of partial delamination needs to be solved numerically from Eqs.(2)and(3). Here an approximate solution is obtained.We notice that the blue curve for partial delamination is very close to a linear line,and two points on this line can be given analytically by Eqs.(9)and(10)and Eqs.(1)and(4)as

The energy curve for partial delamination can be approximated by the straight line connecting the two points in Eq.(11).The intersection point between this line and the wrinkling curve can be then obtained analytically as

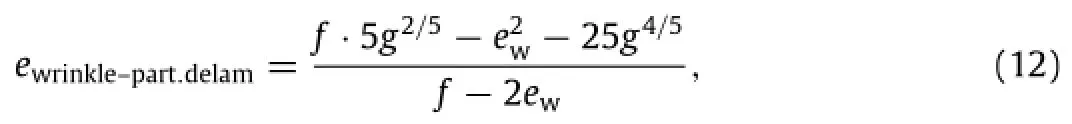
By carefully comparing the energies,one can determine which buckling mode has the lowest energy.However,the relations between these energies depend on the values of ewand g, and therefore require careful investigation of various cases.We categorize these cases by the value of ew=(3Es/E)2/3/(4εc)(an indication of relative stiffness of the substrate)as the following.

(1)0＜ ew≤ 1:for extremely soft substrate,it is found that the energyofthewrinkling modeisalwayslowerthanthoseofpartial and total delamination modes.Therefore,the deformation map is obtained from Eq.(6)as

(

3)3＜ew≤5:the conclusions are the same as Case 2 for weak adhesion ofFor stronger adhesion,the transitions from flat to wrinkling,then to partial and total delamination modes can be obtained from Eqs.(6),(10) and(12)as

(4)ew＞5:for relatively stiffer substrate(note:its Young’s modulusisstillfourtofiveordersofmagnitudelowerthanthat ofthefilm),theconclusionsarethesameastheresultsofWang et al.[23]for weak adhesion ofFor adhesion stronger than that,the transitions are the same as in Case 3:

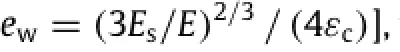
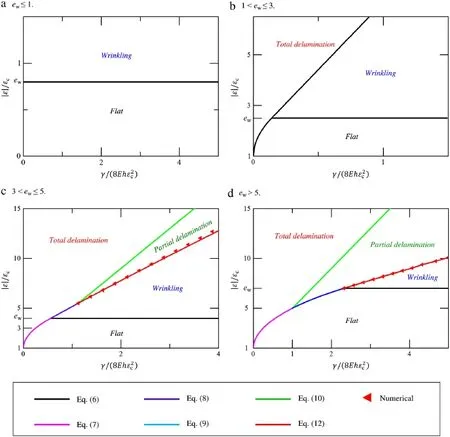
Fig.3.Deformation mapsversusthat separate the four buckling modes for various values of ew;the plots are generated for representative ewvalues of (a)0.8;(b)2.5;(c)4.0;(d)7.0.(For interpretation of the references to color in this figure legend,the reader is referred to the web version of this article.)

Hereweusetheexampleinthepreviousstudies[21,22]toshow theutility ofthepresentedresults.Thematerialandgeometric and mechanical properties[22,23]are E=2.5 GPa,h=1.4µm,L= 150µm,Es=2.0 MPa,andγ=0.16 J/m2,which correspond to thenormalizedvaluesofew=15.6andg=69.6.Underthesetwo conditions,Eq.(16)applies and gives the following results(these can also be obtained from Fig.3(d)):

These results agree very well with experimental observance shown in Fig.4:the film is flat(Fig.4(a))before compression is applied;under very small strain it wrinkles into multiple waves (Fig.4(b))and then quickly transits to the partial delamination mode(Fig.4(c));when|ε|exceeds about 8.5%[23],the film totally delaminated from the substrate(Fig.4(d)),which agrees very well with the 8.0%strain predicted by the analytical model.It should be noted that there may exist another buckling mode between the wrinkling and partial delamination modes,in which the film delaminates from the substrate from multiple locations.However, since the transitions happen at very similar strain levels,we propose to adopt the simplified model presented here.

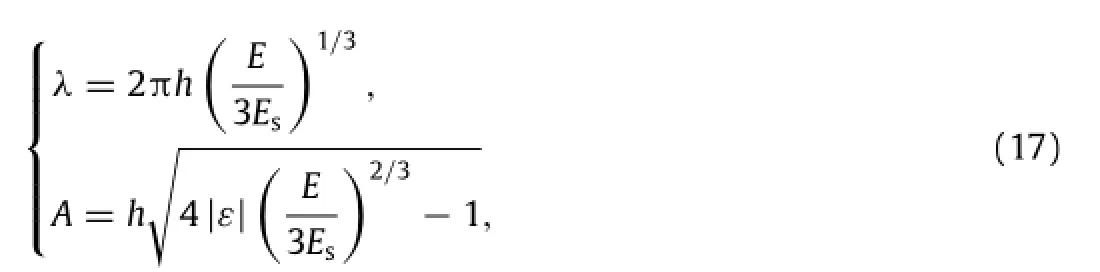
Fig.4.Experimental images of the four buckling modes.

The deformed shape of the film and the peak strain for the flat, partial/total delamination modes are analyzed in detail by Wang et al.[23].For the wrinkling mode,Jiang’s analysis[2]shows that the wrinkling wavelengthλand amplitude A can be obtained by which gives the wavelength to be 67.5µm and agrees reasonably with 56.8µm from experiments(Fig.4(b)).This predicts 2–3 waves over the total span of L=150µm,which again agrees withexperimentalobservations(onlythemiddlewaveofthethree waves in Fig.4(b)spans for an entire wavelength ofλ).Therefore, for the wrinkling mode,we propose to follow Jiang’s approach in Ref.[2]to analyze the maximum strain to prevent fracture of the film structure.

The deformation maps shown in Fig.3 are very important for the design of bio-integrated electronics,in the sense that they predict the buckling modes for any materials under any adhesion conditions.One crucial information they predict is the onset of interfacial delamination,indicated in these figures by the lower bounds of partial and total delamination modes(magenta,purple, cyan and red curves).

In this paper,an analytical model is established for thin-film on elastomer structures in the context of bio-integrated electronics applications.Under different conditions in interfacial adhesion, stiffness of the elastomer(tissues)and the levels of compressive strain,the thin film buckles into various modes.The transitions between these modes are predicted analytically,and summarized infourdeformationmaps.Thelowerboundsofthepartialandtotal delamination modes predict the onset of interfacial delamination, which sets design criteria to avoid delamination and achieve intimate and conformal contact to bio-tissues.The analytically predicted information on deformation modes,maximum strain, and interfacial intactness,are important to the design and optimization of high performance bio-integrated electronics.

Acknowledgment

Theauthorsacknowledgepartialsupportofthisresearchbythe National Natural Science Foundation of China(Grants 11272260, 11172022,11572022,51075327,11302038).

Appendix A.Supplementary data

Supplementary material related to this article can be found online at http://dx.doi.org/10.1016/j.taml.2015.11.010.

References

[1]S.Wang,J.Song,D.-H.Kim,et al.,Local versus global buckling of thin films on elastomeric substrates,Appl.Phys.Lett.93(2008)023126. http://dx.doi.org/10.1063/1.2956402.

[2]H.Jiang,D.-Y.Khang,J.Song,et al.,Finite deformation mechanics in buckled thin films on compliant supports,Proc.Natl.Acad.Sci.104(2007) 15607–15612.http://dx.doi.org/10.1073/pnas.0702927104.

[3]J.Xiao,A.Carlson,Z.J.Liu,et al.,Analytical and experimental studies of the mechanics of deformation in a solid with a wavy surface profile,J.Appl.Mech. 77(2009)011003–011003-6,http://dx.doi.org/10.1115/1.3132184.

[4]Y.Zhang,S.Xu,H.Fu,etal.,Bucklinginserpentinemicrostructuresandapplicationsinelastomer-supportedultra-stretchableelectronicswithhigharealcoverage,SoftMatter9(2013)8062–8070. http://dx.doi.org/10.1039/C3SM51360B.

[5]Z.Li,Y.Wang,J.Xiao,Mechanicsofcurvilinearelectronicsandoptoelectronics, Curr.Opin.Solid State Mater.Sci.3(2015)171–189. http://dx.doi.org/10.1016/j.cossms.2015.01.003.

[6]S.Xu,Z.Yan,K.-I.Jang,et al.,Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling,Science 347(2015) 154–159.http://dx.doi.org/10.1126/science.1260960.

[7]Y.Xue,Y.Zhang,X.Feng,et al.,A theoretical model of reversible adhesion in shapememory surfacereliefstructuresand itsapplicationin transferprinting, J.Mech.Phys.Solids 77(2015)27–42. http://dx.doi.org/10.1016/j.jmps.2015.01.001.

[8]Z.Li,J.Xiao,Mechanics and optics of stretchable elastomeric microlens array for artificial compound eye camera,J.Appl.Phys.117(2015)014904. http://dx.doi.org/10.1063/1.4905299.

[9]H.C.Ko,M.P.Stoykovich,J.Song,et al.,A hemispherical electronic eye camera based on compressible silicon optoelectronics,Nature 454(2008)748–753. http://dx.doi.org/10.1038/nature07113.

[10]G.Shin,I.Jung,V.Malyarchuk,etal.,Micromechanicsandadvanceddesignsfor curved photodetector arrays in hemispherical electronic-eye cameras,Small 6 (2010)851–856.http://dx.doi.org/10.1002/smll.200901350.

[11]S.Wagner,S.P.Lacour,J.Jones,et al.,Electronic skin:architecture and components,Physica E 25(2004)326–334. http://dx.doi.org/10.1016/j.physe.2004.06.032.

[12]S.P.Lacour,J.Jones,Z.Suo,et al.,Design and performance of thin metal film interconnects for skin-like electronic circuits,IEEE Electron Device Lett.25 (2004)179–181.http://dx.doi.org/10.1109/LED.2004.825190.

[13]T.Someya,T.Sekitani,S.Iba,etal.,Alarge-area,flexiblepressuresensormatrixwithorganicfield-effecttransistorsforartificial skin applications,Proc.Natl.Acad.Sci.USA 101(2004)9966–9970. http://dx.doi.org/10.1073/pnas.0401918101.

[14]S.Xu,Y.Zhang,L.Jia,etal.,Softmicrofluidicassembliesofsensors,circuits,andradiosfortheskin,Science344(2014)70–74. http://dx.doi.org/10.1126/science.1250169.

[15]A.Nathan,B.Park,A.Sazonov,et al.,Amorphous silicon detector and thin film transistor technology for large-area imaging of X-rays,Microelectron.J. 31(2000)883–891.http://dx.doi.org/10.1016/S0026-2692(00)00082-3.

[16]D.-H.Kim,N.Lu,R.Ma,et al.,Epidermal electronics,Science 333(2011) 838–843.http://dx.doi.org/10.1126/science.1206157.

[17]L.Xu,S.R.Gutbrod,A.P.Bonifas,et al.,3D multifunctional integumentary membranes for spatiotemporal cardiac measurements and stimulation across the entire epicardium,Nature Commun.5(2014)3329. http://dx.doi.org/10.1038/ncomms4329.

[18]J.Viventi,D.-H.Kim,L.Vigeland,et al.,Flexible,foldable,actively multiplexed, high-density electrode array for mapping brain activity in vivo,Nat.Neurosci. 14(2011)1599–1605.http://dx.doi.org/10.1038/nn.2973.

[19]Z.Y.Huang,W.Hong,Z.Suo,Nonlinear analyses of wrinkles in a film bonded to a compliant substrate,J.Mech.Phys.Solids 53(2005)2101–2118. http://dx.doi.org/10.1016/j.jmps.2005.03.007.

[20]S.Wang,M.Li,J.Wu,et al.,Mechanics of epidermal electronics,J.Appl.Mech. 79(2012)031022–031022-6,http://dx.doi.org/10.1115/1.4005963.

[21]H.Cheng,Y.Zhang,K.-C.Hwang,et al.,Buckling of a stiff thin film on a prestrained bi-layer substrate,Int.J.Solids Struct.51(2014)3113–3118. http://dx.doi.org/10.1016/j.ijsolstr.2014.05.012.

[22]H.C.Ko,G.Shin,S.Wang,et al.,Curvilinear electronics formed using silicon membrane circuits and elastomeric transfer elements,Small 5(2009) 2703–2709.http://dx.doi.org/10.1002/smll.200900934.

[23]S.Wang,J.Xiao,J.Song,et al.,Mechanics of curvilinear electronics,Soft Matter 6(2010)5757–5763.http://dx.doi.org/10.1039/C0SM00579G.

13 October 2015

in revised form 14 November 2015

http://dx.doi.org/10.1016/j.taml.2015.11.010

2095-0349/Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

∗.

E-mail address:shuodao.wang@okstate.edu(S.Wang).