The finite deformation of the balloon catheter

Jian Wu∗,Zhuangjian Liu

aAML,Department of Engineering Mechanics,Tsinghua University,Beijing 100084,China

bCenter for Mechanics and Materials,Tsinghua University,Beijing 100084,China

cInstitute of High Performance Computing,1 Fusionopolis Way,#16-16 Connexis,138632,Singapore,Singapore

Letter

The finite deformation of the balloon catheter

Jian Wua,b,∗,Zhuangjian Liuc

aAML,Department of Engineering Mechanics,Tsinghua University,Beijing 100084,China

bCenter for Mechanics and Materials,Tsinghua University,Beijing 100084,China

cInstitute of High Performance Computing,1 Fusionopolis Way,#16-16 Connexis,138632,Singapore,Singapore

H I G H L I G H T S

•We developed an analytical model to determine the shape of inflatable catheter.

•The devices integrated on the catheter can be located by the mechanics model.

•The latitudinal elongation is much larger than the longitudinal elongation of inflated catheter.

A R T I C L EI N F O

Article history:

Accepted 20 November 2015

Available online 24 December 2015

Balloon-based catheter

Stretchable electronics

Expansion

The balloon-based catheters are attractive for the minimally invasive procedures because these catheters can be configured to match requirements on size and shape for the interaction with the soft tissue.An analytical mechanic model is developed for the deformed balloon to determine the shape of the inflated catheter.The bridges along latitudinal direction should be high stretchable due to the high elongation along the latitude of the inflatable catheter.These results agree well with the finite element method without any parameter fitting.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://

creativecommons.org/licenses/by-nc-nd/4.0/).

Catheters are widely-used surgical tools for minimally invasive procedures to improve human health[1–6].Devices and sensors are integrated on catheters to establish biocompatible interfaces between the semiconductor devices and the soft,curvilinear surfaces of the body.Balloon-based catheters are designed as heterogeneous collections of minimally-invasive medical devices which are integrated on the deformable skin of catheters.As shown in Fig.1,the balloon-based catheters can be stretched up to 200%[7].The limitation of the integration of electronic system is overcome to integrate devices and sensors on the catheter due to the high stretchability of the catheter skin.Consequently,a key point of the balloon-based catheter is to determine the locations of the different devices and the elongation between the devices while the catheters are inflated,which is necessary for the use of catheters during procedures.

As shown in Fig.2(a),the deflated catheter is cylindrical,whose lengthandradiusare2LandR0,respectively.Afterairisblown into catheter,the catheter skin will be expanded to a balloon,whose maximum radius is R shown in Fig.2(b).The inner layer of catheter is almost undeformed since the inner layer is much thicker than the catheter skin,and the length of inflated catheter is fixed as 2L during the catheter skin expanding,which cross section can be described as an ellipse,

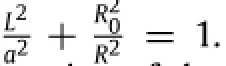
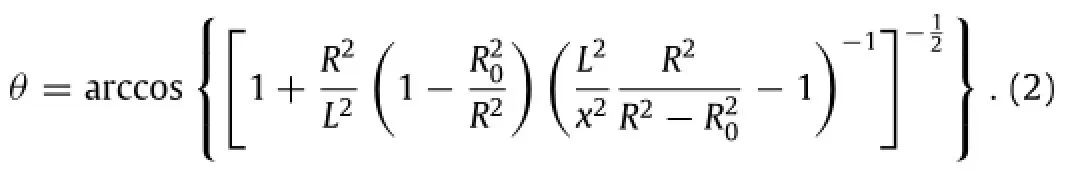
The arc length of the ellipse,ds,is

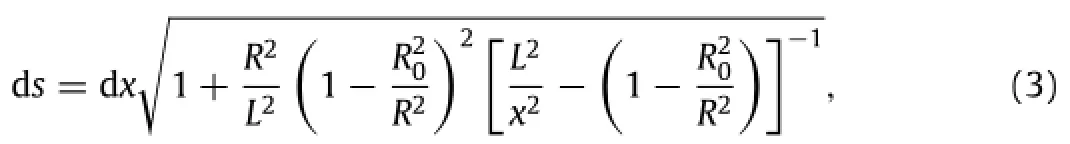
http://dx.doi.org/10.1016/j.taml.2015.11.009

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Fig.1.Multifunctional inflatable balloon-based catheter.(a)Optical image of a stretchable,interconnected mesh integrated on a deflated catheter;(b)optical image of the inflated balloon catheter.

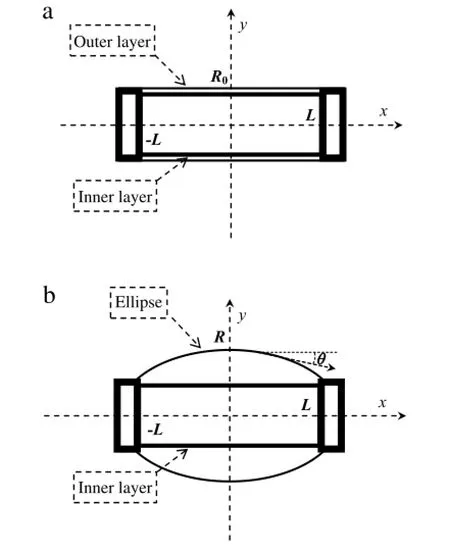
Fig.2.Schematic diagrams of the balloon catheters.(a)Deflated catheter with outer and inner layers;(b)inflated catheter with ellipse and undeformed inner layer.

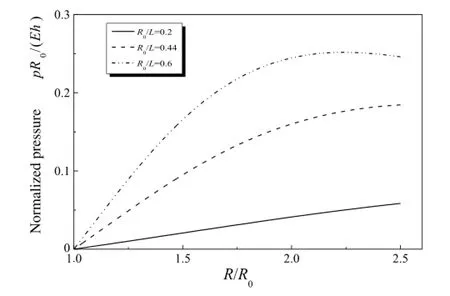
Fig.3.The normalized pressure,versus the ratio,R/R0,for R0/L=0.2,0.44, and 0.6.

whichisdeformedfromtheinitiallengthdX ofthecylindricalshell. The relationship between ds and dX can be given by the elongation εalong the tangent direction of the ellipse as

The equilibrium equation along x axial direction can be obtained from an ellipsoidal shell[8]as tcosθ+∫Lxpdy=0,where p,t are thepressureofblownairandthestressalongthetangentdirection ofballooncatheter,respectively.Thestresscanbederivedfromthe above equilibrium equation as

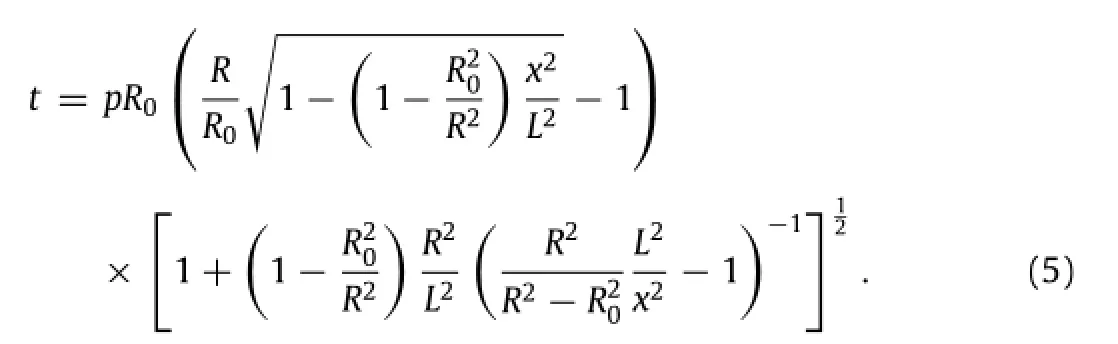
The stress is related to the elongation by the constitutive relationship,t=Ehε,where E,h are the elastic modulus and thickness of the catheter skin.

The initial length X can be given as in Box I.

Because the normalized pressure satisfied the condition, Eq.(6)can be expanded as the Taylor series of the normalized pressure,as

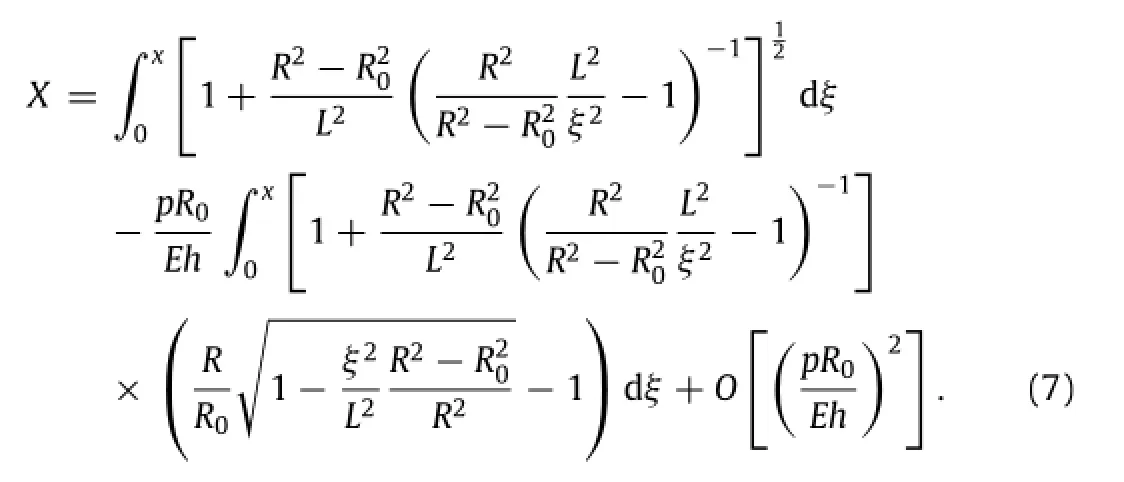
The normalized axial and radical displacements,can be given as

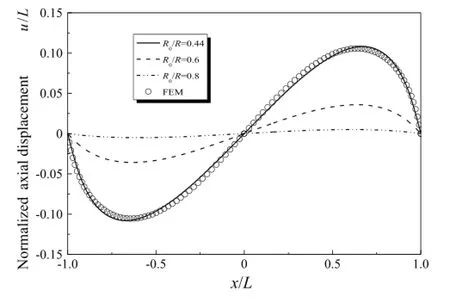
Fig.4.Plot of the normalized axial displacement,,versus the normalized axial position,,for0.6,and 0.8 that shows good agreement between the analytical solution and the finite element analysis for

The finite element method was also used to determine the deformation of the catheter.Four-node shell elements in the finite element analysis software ABAQUS are used to determine the deformation of the balloon catheter.Figure 4 shows the normalized axial displacement,versus the normalized axial position,for,and 0.8 with R0/L=0.44.The maximum values of the axial displacement appear around locations which distances are one-sixth of length fromthe ends.Figure 5 shows the normalizedradicaldisplacementversusthenormalizedaxialposition,,for0.6,and 0.8 withFigures 4 and 5 show that the analytical solutions from Eqs.(9)and(10)agree well with the results of the finite element method without any parameter fitting.Therefore,Eqs.(9)and(10)can be used to determine the positions of the expanded catheter.The latitudinal elongation of the expanded catheter,which is equal to the normalized radicaldisplacementinFig.5,ismuchlargerthanthelongitudinalelongation shown in Fig.6.Therefore,the stretchability of the serpentine bridges along the latitudinal direction should be much higher than the bridges along the longitudinal direction for the use of the balloon catheter during procedures.

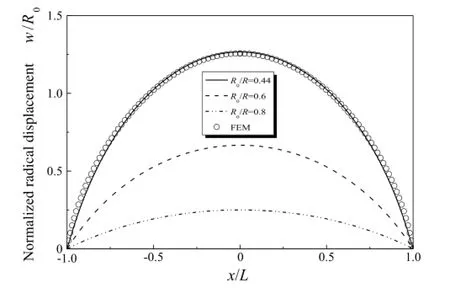
Fig.5.Plot of the normalized radical displacement,versus the normalized axial positionfor,and 0.8 that shows good agreement between the analytical solution and the finite element analysis for

Acknowledgments

J.W.acknowledges the supports from the National Key Basic Research Program of China(Grant No.2015CB351900),National NaturalScienceFoundationofChina(GrantNo.11202113),andthe Ministry of Education of China(Grant No.201327).

References

[1]S.I.Seldinger,Catheterreplacementoftheneedleinpercutaneous arteriography—a new technique,Acta Radiol.39(1953)368–376.

[2]B.J Scherlag,S.H.Lau,R.H.Helfant,Catheter technique for recording his bundle activity in man,Circulation 39(1969)13.

[3]R.Mueller,T.Sanborn,The history of interventional cardiology,Am.Heart.J. 129(1995)146–172.

[4]R.M.Donlan,J.W.Costerton,Biofilms:Survival mechanisms of clinically relevant microorganisms,Clin.Microbiol.Rev.15(2002)167–193.

[5]K.Nademanee,J.McKenzie,E.Kosar,A new approach for catheter ablation of atrial fibrillation:Mapping of the electrophysiologic substrate,J.Am.Coll. Cardiol.43(2004)2044–2053.

[6]J.Huang,Q.-Y.Yuan,Z.-W.Zhu,Catheter-based transendocardial microbubble and pEGFP delivery combination of intracardiac ultrasonic exposure enhances EGFP gene expression,Int.J.Cardiol.145(2010)583–584.

[7]D.-H.Kim,N.Lu,R.Ghaffari,et al.,Materials for multifunctional balloon catheterswithcapabilitiesincardiacelectrophysiologicalmappingandablation therapy,Nature Mater.10(2011)316–323.

[8]S.Timoshenko,S.Woinowsky-Krieger,TheoryofPlatesandShells,McGraw-Hill Classic Textbook Reissue Series,New York,1959.

20 October 2015

in revised form 14 November 2015

∗at:AML,Department of Engineering Mechanics, Tsinghua University,Beijing 100084,China.

E-mail address:wujian@mail.tsinghua.edu.cn(J.Wu).