高中数学专题复习课的教学探讨——以高中数列求和的常用方法复习教学为例

熊厚坚

（三明市第二中学，福建 三明 365000）

高中数学专题复习课的教学探讨——以高中数列求和的常用方法复习教学为例

熊厚坚

（三明市第二中学，福建 三明 365000）

数学复习课的教学是学生数学学习能力提升过程中至关重要的一个环节，是扎实数学基础知识、基本技能的重要途径。文章结合教学过程中对复习教学的认识和实践作初步的探讨。

数学复习；教学情境；问题引领；精例题选；时归纳

数学专题复习课的教学是高中数学中至关重要的一项内容，是基础知识和基本技能教学的核心。回顾自己这十几年的教学历程，教学风格基本上是充分利用课堂40分钟，高密度、大容量、快节奏的教学方式。随着生源质量的不断变化，感觉到原有的传统教学风格已不能再适应新的考试改革，特别是2016年高考福建省重新回归使用全国卷，在试题难度与试题命制的风格上有较大不同，学生的考试成绩与期望值相差甚远。一直以来复习课上，教师都采用对复习内容进行知识罗列、讲解例题、练习巩固、课堂小结的模式，虽然看起来好像也有启发、引导，但实质上还是教师讲、学生听、记笔记的被动式教学方法，缺少学生主动探究、主动参与的过程体验。因此，引发笔者思考的是，要去学习，要去改变教学策略，改进方法，要让学生从单向接受性、被动性的学习模式转化为自主性、主动性的学习模式。真正感受到课堂上的师生互动,生生互动交流分享的和谐氛围。经过教学实践尝试，笔者认为，应从以下四个方面着手，激发学生主动地参与复习意识，提高不同层次学生的学习效率。

一、巧设课堂教学情境，点燃学生兴趣

过去总认为不是新授课，教学情境可有可无。其实，复习课中课堂情境非常重要，每堂课都是一开始就知识的梳理，学生非常厌烦，没有兴趣，学习的效率也就可想而知了。因此设计合理情境，串起课堂的主线，保证教学的新颖性、有效性，能让学生自然深入地进行学习状态。笔者所任教的两个班，一个班采用直接进入复习主题，另一个班采用设置教学情境导入主题，明显感觉到学生学习的热情完全不一样。笔者在上《数列求和》这节复习课时，从温习两个小故事开始：

故事1：数学家高斯十岁时，仅用几秒钟算出从1一直加到100。

故事2：国王要重赏国际象棋发明者西塔，西塔只要在他的棋盘上赏一些麦子就行了，在棋盘的第1个格子里放1粒，在第2个格子里放2粒，在第3个格子里放4粒，在第4个格子里放8粒，依此类推。

两个故事体现的数学知识，那就是数列的前n项和，今天这节课我们就一起来系统地复习数列求和。首先一起回顾哪些数列的前n项和公式我们是已经知道的：（全体学生一起回答）

（等学生回答完后，展示课件内容），还有呢？

2.等比数列前n项和公式：（提问学生，师生一起回答，媒体展示）

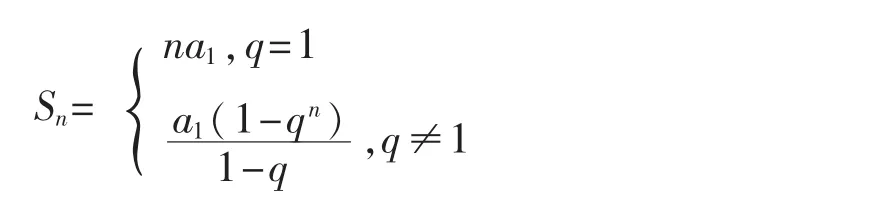
教师加以强调：这个公式提醒学生当公比q是参变量时，特别要对q的值进行讨论，分q等于1和不等于1。

在课堂中施以教学情境，让学生对知识感到新鲜，从而产生强烈的学习探索欲望。但是情境的创设也应根据情况具体问题具体分析，并不是处处都需要，有时过多引入现实情境反而会使教学内容产生逻辑混乱。在创设情境的选择上，以能否承载数学知识与教学内容紧密相联作为标准，否则将导致舍本逐末、画蛇添足。

二、用问题串起知识主线，引领学生完善理解

一节内容开始复习时，总要对知识要点进行梳理，它好像是一部戏的开场锣鼓。以前总是教师一个人来敲打，效果大打折扣。现在尝试让学生大家一起合奏，把知识要点设计成问题串，层层递进，串起整节课的知识主线，从而让学生完善理解。笔者在《数列求和》这节复习课中通过设置下面的问题串来帮助理清知识脉络。

思考1：等差数列的前n项公式是如何推导？

提问学生，根据学生回答情况纠正，引出这是一种常见的求和法，这种方法称之为倒序相加法，再一起看例1

例1:求sin21°+sin22°+sin23°+…+sin288°+sin289°

引导学生观察这个问题，思考如何解决？首先从正弦的角度数变化规律看是从1°到89°而不是1°到88°或1°到90°，这1°和89°有何关系？2°和88°呢？……两个角互为余角，大家自然联想到诱导公式你又会得到什么结论？（板书，α+β=90°，则sinα=cosβ）题目又是以平方和的形式呈现给我们，同角的正弦与余弦又存在什么关系？这样对本题应如何下手？

提问学生，根据学生回答情况纠正，让学生发现这个问题可采用倒序相加法。展示课件解答过程。

同学们发现头尾有规律，利用了组合数公式，对采用倒序相加法求和创造了极好的条件，于是，又有如下的解法。（展示课件解答过程）

思考2：等比数列的前n项和公式是如何推导？

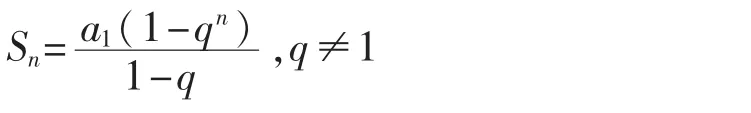
提问学生：学生边讲边引导，并展示课件中推导过程。这种方法称为错位相减法，可以解决一类求和问题。

例2：求Sn=a+3a2+5a3+…+（2n+1）an（a≠0）

请学生齐声回答，这个问题用什么方法解决？提示学生并分析刚才推导过程中数列的特征，数列的每一项可以视为一个等差数列与一个等比数列的乘积，可用错项相消法。师生一起回顾书写过程。

这时应该如何操作？（在上式两边乘上1/2后错位相减）

但，若把上式中的×改为+，则问题变为

此时，还能实施错项相消法吗？于是，通过观察结合已学的等差与等比数列的特征进行分析，可将此数列分组，一组用等差数列求和法，一组用等比数列求和法，即：分组求和法来达到问题解决目的。

1.分组求和法

同学们观察上面这个数列有什么特征？如何来求？提问学生：学生边回答老师边补充完整。师生总结发现Sn是一个等差数列交替间隔一个等比数列求和的形式，本质是数列的前n项和，显然我们只要通过加法交换律对此数列各项进行重组这个和式，转化成了大家熟悉的等差、等比数列的求和。这种求和的方法我们称之为分组求和法。

2.并项求和法

请同学们看例4

引导学生相邻两项组合发现有规律，可以用平方差公式，接着板书，整理后发现，原式会等于－（1+2+ 3+…+100），这正是我们熟悉的求和，结果等于－5050.在这个问题当中，通过合并相邻的两项，转化为熟悉的结构，达到了求和的目的。

3.裂项相消法

数学就是那样的微妙，大家应该还记得，如果一个数列，我们如果能将它分为正负两项，在求和中与上面一样，同样出现正负交替，但它们却会在求和中相互抵消，最终剩下有限几项，这种求和方法我们又可称为什么？裂项相消法。一起看例5

例5:（1）在数列｛an｝中，，，求数列｛bn｝的前n项的和.

第2小题，请一位同学到黑板上板书。学生做完后，讲评。首先看裂项，提醒学生前面还要乘以，因为括号里通分后与原式比多乘了2，接着提醒到底哪些项可以消去，提示还有一种写法

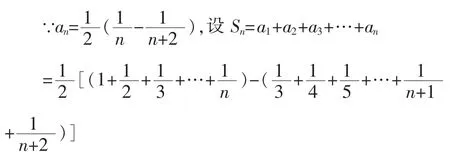
前后各有两项不能消去

注意:使用裂项相消时，应注意消去了哪些项，保留了哪些项，保留的项具有前后对称的特点。

通过以上一系列环环相扣的问题的思考，将数列求和常见的五种方法扎实的联系起来，并有序地延展下去，让知识不断地深化发展。

三、用合适例题巩固知识，引导学生积极思考

合适的例题能为学生分析问题、解决问题提供原型和模式，促进学习迁移。所以，笔者在本节课的设计中，每一个问题都设置对应例题加以巩固，这在复习中往往具有特殊效果，在第二大点中，笔者已经对例题的设置进行了阐述，这里不再列举。例题不能仅仅是追求解答结果，更重要的是通过题目促进学生掌握一类问题、一类方法。所以，题目类型要精选，要覆盖复习的所有内容，综合性要比较强，还要注意题型的变式、迁移。这样能使学生学得更加主动，理解更加深刻，灵活性与创造性得到有效的培养。

四、用简短语句归纳小结，拓展学生知识视野

在每个例题解答之后，教师与学生一起回顾复习过程，总结问题解决过程运用的数学思想方法、基本策略，切实提高学生的数学思维能力。本节课中，笔者对每个方法后面都进行适时的小结与归纳，如：倒序相加法的特点是数列中首末两端的项为等 “距离”的两项，求和时可把求和式中各项从第1项至最后一项顺写与各项从最后1项至第1项用倒写的两个式子相加，就得到一个常数列的和的2倍，或者构建出常项的因式，这类求这个数列的前n项和问题可用倒序相加法，它是等差数列的前n项和求法标志性特征。

总之，课堂教学研究没有止境，在课堂上要充分以学生为主,关注如何调动学生的积极性,给学生参与课堂营造氛围；给学生自主探究时间与空间；给学生相互交流、展示、用数学语言表达数学问题解决方法、规律,通过师生交流合作，让学生能轻松愉快地进入学习、思考状态，更好地掌握数学知识，不断提高数学素养。

［1］李明照.“问题探究式”教学在高中数学课堂的实践与思考［J］.数学教学研究，2005（8）.

［2］袁竟成.一堂关于直线和圆的建构式习题课［J］.数学教学，2004（3）.

［3］伊海.数学教学与生活相结合的尝试和感受［J］.福建基础教育研究，2013（2）.

G633.6

A

1673-9884（2016）08-0041-03

2016-07-17

熊厚坚（1983-），男，福建宁化人，三明市第二中学一级教师。