数学在平面设计中的应用
2016-12-08万莹
万 莹
(信阳农林学院 规划与设计学院,河南 信阳 464000)
数学在平面设计中的应用
万 莹
(信阳农林学院 规划与设计学院,河南 信阳 464000)
数学与艺术一样,是人性建构自身的理性需要,抽象是高级思维的一个标志,理性思维、严密推理中同样会有灵感巧思的不期而至。所以,数学与音乐、文学、绘画等都有着千丝万缕的关系,与平面设计方向的联系也颇为显著,像版式设计、海报设计、书籍设计等都会用数学这门思维缜密的学科来创造出无穷为例的艺术作品。
数学;比例;平面构成
数学是研究数量、结构、变化以及空间模型等概念的一门学科。透过抽象化和逻辑推理的使用,由计数、计算、量度和对物体形状及运动的观察中产生。因此,数学有着抽象的思辨,严密的推理,逻辑的论证和精确的计算,总揽全局而又步步为营的思维方式。而艺术是一种文化现象,大多为了满足主观与情感的需求,也是日常生活进行娱乐的特殊方式。其根本在于不断创造新兴之美,借此宣泄内心的欲望与情绪,属浓缩化和夸张化的生活。所以,艺术是对哲学思想的变迁,是艺术家们对多变的技术环境反馈最直接的表现形式;艺术是浮想联翩、蔑视规律的,弥漫着一种说不清道不明的艺术图景。表面来看,数学和艺术好像是没有关系的,但是,仔细考察人类历史和现实,我们不难发现,几乎人类的一切学科领域都或多或少用到数学,艺术也不例外,细细品味,好像数学的语言和思想都可以贯穿于五彩缤纷的艺术生活之中,鉴于辩证唯物论,任何事物都是辨证统一的,数学与艺术也蕴涵着内在的统一[1]。
1 艺术中的数学要素
自古以来,人们对美的界定始终涉及到对象的对称性、和谐与秩序,这是一种定性的描述。18世纪荷兰哲学家赫姆斯特休斯认为,艺术的美是在最小时间间隔内传达出最大量的观念。1935年美国数学家柏克霍夫分析了审美经验,也作了一种定量化的尝试。他提出这样三个要素:①为了正确关照和把握对象,需要付出的努力与对象的复杂性c成正比;②关照对象时所取得的愉悦感受是对审美价值的量度(审美度M);③有意识的知觉是对具有一定和谐或秩序o的对象的关照。这三种要素之间构成如下关系:M=o/c,即审美度=秩序/复杂性。
这并不是给出一种美的定义性公式,而是说明审美效应与上述要素相关,对这些要素的测定具有一种客观的和数学的性质。应用这种公式可以对同类的审美对象进行一种客观评价[2]。以花瓶为例,在这里不考虑人们由其历史背景造成的不同趣味崇尚以及装饰因素的影响。用花瓶的屏幕图形作为表征,在观察花瓶时,引起人视觉注意的点主要有以下几种类型:①由轮廓线所决定的四个点;②轮廓线上具有垂直或水平方向的切线的点;③方向突然改变的点;④曲线经过零的转折点。这些都是特征点,起切线方向则为特征方向。人们的注意力只集中在这类特征要素之上,复杂性c即可用这些特征点的总数来衡量,通常花瓶的c不超过20。引起审美趣味的、与秩序相关的要素包括四项,它们是由特征点的水平线及花瓶轴线垂直线的关系组成。其中v为垂直长度之间的关系数,h为水平线总长之间的关系数,hv相当于这两种距离类型之间的均匀关系,t为花瓶一边各特征点切线方向之间的关系。各要素之间的关系为:M=h+v+hv+t∕c。
2 数学在平面设计中的应用
在现代的二维和三维设计中,常常会见到类似数学秩序进行形态变化的方法。就从平面设计这一方向来说,它的比例与分割都是与数学有着内在的联系。比例关系的应用对于建立画面的统一秩序有着重要的作用。比例是指某一对象局部与局部或整体与局部的相对关系,它不涉及具体的尺寸,但与比率有关。比率是指两个相似事物之间的数量比。当我们描绘物象的真实形象时,常常不是按对象的实际大小表现,而是先分析对象的比例关系,再按同样的比例转换到画面中。它们的大小虽然可以改变的,但它们之间的比例关系是等同的。以数学逻辑为基础进行分割,或取用不同的比率进行分割,会直接影响画面的整体结构,造成不同的视觉效果。比较常用的比例分割方法有等份分割、黄金分割、平方根矩形分割、渐变分割、等比分割[3]。
2.1 等份分割
等份分割就是将画面以二等份、三等份、四等份等平均分割,线以等间隔方式排列的简单而严谨的分割方法。如此就像我们常用的二方连续、四方连续,而且在古代的纹饰上就能体现出来,特别是楚纹饰,它在对空间的处理和把握上做得非常巧妙,即使庞杂的图案也能巧夺天工地进行组织安排,完美体现了楚纹饰绮丽流畅的视觉效果。
等份分割有一种对称之美,对称的美感源自于这种等份分割的稳定感,无论是多么富有动感的视觉元素,经过分割排列处理之后,便会产生稳定感。分割排列还能表现出一种完整性,无论是多么支离破碎的视觉元素,在平均分割的状态下都会趋于完整。这种有规律的重复编排,能使任何杂乱的视觉元素产生某种节奏美。
2.2 黄金分割
黄金分割是一种数学上的比例关系,也就是我们所熟悉的黄金比例,是由希腊人发现的,它从人体的比例中产生,具有严密的比例性、艺术性、和谐性,蕴藏着丰富的美学价值。希腊的神殿和米罗的维纳斯雕像的基本尺寸亦用了黄金比,因而被称为神圣的比例。它被当作支配大自然和生灵万物的结构,并作为支配艺术结构原理的规范,它所分割的形,具有整体的协调性。从古希腊开始到现在,仍被绘画、设计、建筑等领域所应用。
黄金比是含有无理数的数字。我们一般取至小数点以后第三位数,即1.618。数学中的3∶5、5∶8、8∶13等最为接近这种黄金比[4]。生活中有许多让人觉得很美的东西,像松果,它有8条顺时针生长线和13条逆时针生长线,就得到了8∶13这个比值。还有向日葵,有21条正旋螺旋线,34条逆旋螺旋线(如图1),形成的比例是1∶1.619,非常接近黄金分割率。所以说,黄金分割的比例关系能够给画面带来令人愉悦的形状。

由图2可以简单理解黄金分割矩形的形成:
①一个正方形边线的中点A向对角B画一条斜线,以斜线为半径画出的弧线,与正方形的延长线相交于C点。构成一个黄金矩形;
②大矩形和小矩形的对角线和边线的相交点,成为黄金二次分割的起始线;
③这个分割过程可以无限继续下去,产生许多更小的等比的矩形和正方形。
2.3平方根矩形分割
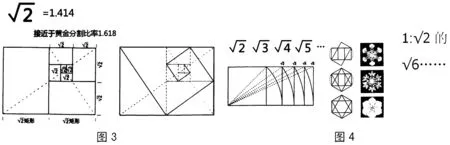
3 结束语
由以上这几个例子可以看出,数学与平面设计是紧密联系的。但是这种联系不仅仅只表现在平面构成这一个地方,在图形创意设计中也能够表现出来。像我们每天都能接触和阅读到的符号与数字,摇身一变就可能成为一个个关键的点、线的构成,既把其原本的意义展示出来,也把其图形上的审美表现出来。所以说,艺术是美的表达方式,数学是美的语言,数学追求美,也创造美,数学与艺术的结合使美更加简明。随着人们物质生活的日益提高,对自然精神生活的享受也会提升到更高的层次。就算是我们日常生活中随处可见的广告、海报、宣传品等平面设计,为了吸引观众的眼球,就必须运用数学鬼斧神工的创造力来产生艺术的无穷魅力[5]。
[1] 程江海. 中心投影与平行投影在中西绘画中的应用[J].科技资讯,2008(12):219.
[2] 吴 翔. 设计形态学[M].重庆:重庆大学出版社,2008:4.
[3] 夏镜湖. 平面构成[M].西南师范大学出版社,2006:6.
[4] 王 庚. 数学文化和数学教育[M].北京:科学出版社出版社,2004:111-128.
[5] 易南轩. 数学美拾趣[M].北京:科学出版社,2001:32-37.
[6] 陈珊妍.图形创意设计[M].东南大学出版社,2008:5.
(编辑:严佩峰)
The Application of Mathematics in Graphic Design
WAN Ying
(College of City Planning and Arts Design,Xinyang Agriculture and Forestry University,Xinyang 464000, China)
Mathematics, like the arts, is the rational need of human nature to construct their own. Abstract is a sign of senior, rational thinking. Strict reasoning will also have inspiration of opportunely unbidden. So, mathematics and music, literature, painting and so on, all have the countless relationship. Format design, poster design, book design all ues mathematics which is a meticulous thinking subject to create an art work.
mathematics; proportion; tow dimentional composition
2016-09-15
万 莹(1988—),女,河南信阳人,硕士,助教,主要研究方向:环境艺术设计.
J511
A
2095-8978(2016)04-0115-03
