混凝土握裹层径向压力对带肋钢筋黏结性能影响试验研究

王 立 成， 李 龙 龙， 梁 永 钦

( 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024 )



混凝土握裹层径向压力对带肋钢筋黏结性能影响试验研究

王 立 成*， 李 龙 龙， 梁 永 钦

( 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024 )

对于带肋钢筋的黏结性能，钢筋横肋与混凝土之间的咬合力起控制作用．混凝土握裹层的径向压力是研究带肋钢筋横肋与混凝土之间相互作用的重要条件．通过拉拔黏结试验测量了劈裂破坏过程中混凝土握裹层作用在带肋钢筋上的径向压力．试验中，在钢筋内开槽布置两个微型荷载传感器测量混凝土握裹层的径向压力，通过对6个试件开展拉拔黏结试验测定了不同厚度混凝土握裹层的约束作用．试验发现，在试件劈裂破坏过程中，钢筋肋前有效角不断变小，黏结应力与混凝土握裹层的径向压力成正比；试件劈裂破坏时，钢筋肋前有效角与保护层厚度成反比，黏结应力沿锚固段的分布受到保护层厚度的影响：当保护层厚度适中时，黏结应力分布均匀．另外，试验测得的混凝土握裹层径向压力最大值与考虑裂缝黏聚力的厚壁圆筒理论模型预测值吻合较好．

带肋钢筋；混凝土握裹层；约束作用；劈裂破坏；机械咬合作用

0 引 言

钢筋和混凝土间良好的黏结性能是两种材料能够共同工作承受荷载的关键因素之一．对于带肋钢筋，横肋与混凝土的咬合作用，使其黏结锚固性能优于光圆钢筋，所以在工程实际中得到了广泛应用．带肋钢筋通过横肋的咬合作用将自己的轴力传递给握裹层混凝土时，会产生平行于黏结面的黏结应力和垂直于黏结面的径向压力．以前的试验主要关注黏结应力或钢筋的黏结滑移本构关系．例如，Lutz等[1]通过试验揭示了混凝土握裹层的应力状态和裂缝的扩展规律，指出变形钢筋和混凝土之间的黏结作用包含化学胶着力、摩擦作用和机械咬合作用．Goto[2]采用在黏结区注入墨水的办法，揭示了混凝土握裹层裂缝的分布形态并给出了裂缝的发展模型．Eligehausen等[3]通过试验分别研究了在单调和循环荷载作用下带肋钢筋的黏结滑移本构关系，提出了四段式黏结滑移本构模型．宋玉普等[4]通过试验测定了钢筋混凝土梁中纵向钢筋的应变分布，并辅之理论分析得到了连续型的黏结滑移本构模型．徐有邻等[5]通过试验也给出了混凝土握裹层裂缝的发展过程，提出了五段式黏结滑移本构关系和对应的四个特征强度计算模型．对于握裹层的径向压力，Clark等[6]采用带圆柱形空腔的混凝土试件，通过在空腔内施加静水压力胀裂混凝土保护层，测定了不同厚度保护层能够承受的最大径向压力．在理论方面，Tepfers[7]首先采用了厚壁圆筒模型来预测混凝土握裹层的最大径向压力．文献[8-9]通过考虑裂缝间的软化效应改进了厚壁圆筒模型．

带肋钢筋和混凝土具有良好的黏结性能．这主要是因为钢筋横肋与混凝土的相互作用，不仅增大了摩擦作用，还引入了机械咬合机制．混凝土握裹层的径向压力是揭示钢筋横肋咬合作用机理的重要条件．以往的试验和理论研究主要关注混凝土握裹层的最大径向压力，很少研究由于钢筋横肋咬合作用引起的最大径向压力，缺少对整个黏结滑移过程中混凝土握裹层径向压力变化规律的研究．基于以上考虑，本文通过特殊设计的试验方法测量黏结滑移过程中，混凝土握裹层作用在变形钢筋上的径向压力，以研究钢筋肋前有效角的变化规律和钢筋横肋与混凝土的咬合作用机理，验证考虑裂缝间黏聚力的厚壁圆筒模型，进一步揭示带肋钢筋的黏结锚固机理．

1 试验概况

1.1 测量原理

为了测量在黏结滑移过程中混凝土握裹层作用在带肋钢筋上的径向压力，将钢筋沿纵肋对称地切成两半．图1(a)为钢筋劈成两半开槽后和两半钢筋合拢后的照片；图1(b)为一半钢筋的开槽示意图和微型荷载传感器的布置方法．每半钢筋在接近两端的位置各开一个20.4 mm×22.0 mm、深4.7 mm的槽，用来布置微型荷载传感器．沿钢筋的轴心开2 mm×3 mm的槽用来将微型荷载传感器的引线引出．在钢筋锚固段的中部开两个直径10 mm、深5 mm的圆槽，用来放置定位销．定位销的作用是只允许两半钢筋相向平移，防止一半钢筋绕两个微型荷载传感器受力点的连线旋转而导致两半钢筋的一侧边缘挤压在一起．在定位销上涂润滑油，避免当两半钢筋发生相向位移时，定位销产生阻力．钢筋上的槽都为暗槽，不会破坏黏结段钢筋的外表面．钢筋的加载端加工两个凹槽，方便加载时夹具固定．荷载传感器采用纽扣式微型荷载传感器，传感器外形尺寸见图2．

(a) 钢筋内开槽和合拢后照片

(b) 钢筋开槽和荷载传感器布置示意图

图1 钢筋加工示意图

Fig.1 Schematic of processed steel bars

图2 微型荷载传感器外形尺寸(单位：mm)

根据钢筋不同的保护层厚度，微型荷载传感器选用两种量程：9.8 kN和19.6 kN．

在握裹层径向压力作用下，钢筋的受力简图如图3所示．每半钢筋可以看作支撑在微型荷载传感器上的简支梁，通过支座反力可以计算出混凝土握裹层作用在钢筋上的径向压力．采用本文介绍的考虑裂缝间黏聚力的厚壁圆筒模型预估最大径向压力约为8 MPa．通过有限元分析，每半钢筋在预估的最大径向压力作用下，跨中挠度最大，约为0.2 mm．微型荷载传感器达到量程时的压缩量为0.2 mm．合拢后，两半钢筋间的净距在1.6±0.6 mm范围内．综合考虑到钢筋的最大挠度和荷载传感器的压缩量，两半钢筋的最大相向位移约为0.6 mm，小于两半钢筋间的净距．采用环氧树脂将合拢后钢筋两侧的缝隙密封，防止浇筑混凝土时水泥砂浆的流入，从而保证在钢筋滑移过程中，两半钢筋间只有微型荷载传感器传力．

图3 握裹层径向压力作用下钢筋受力简图

1.2 测量方法

本文采用拉拔黏结试验测定混凝土握裹层作用在带肋钢筋上的径向压力．将直径25 mm的带肋钢筋，按1.1中的方法布置好微型荷载传感器后固定在专门钢模板中浇筑混凝土．按不同的保护层厚度(24.5、34.5、48.5 mm)，试验设置3组，每组2个试件．同时浇筑3个150 mm立方体伴随试件，用来确定混凝土的抗压强度．采用42.5级普通硅酸盐水泥，配合比为m(水泥)∶m(砂)∶m(石)∶m(水)=1∶0.8∶3.033∶0.617．3个立方体伴随试件抗压强度平均值为21.6 MPa．钢筋合拢后的缝隙方向垂直最小保护层的方向，使劈裂破坏时保护层的顺筋裂缝近似与两半钢筋间的缝隙在同一平面内．这样可以使钢筋内的荷载传感器正好测量到整个劈裂过程中握裹层的径向压力，并且与理论模型的假设相一致．试件尺寸和钢筋位置见图4．钢筋的黏结长度为125 mm，两端各有一段与混凝土的非黏结段，加载端的非黏结段长度为10 mm，自由端的非黏结段长度为15 mm．

(a) 侧视图

(b) 正视图

图4 试件尺寸(单位：mm)

Fig.4 Dimensions of specimen (unit: mm)

图5是加载装置示意图．在试件加载端安装两个位移传感器(LVDT)，用于量测加载端的滑移；拉拔力通过安装在钢筋加载端上方的荷载传感器获得，握裹层的径向压力通过埋在两半钢筋之间的微型荷载传感器测得．采用1 000 kN 液压伺服试验机进行加载，数据通过IMC采集设备进行连续采集．试验加载方式采用位移控制，加载速率为0.5 mm/min．

图5 拉拔试验加载装置示意图

1.3 试验结果及分析

各试件均为劈裂破坏，图6为劈裂破坏试件的照片．照片中钢筋横肋前的白色碎屑是挤碎的水泥浆．劈裂破坏时各荷载传感器的测量值见表1，其中R1为埋在钢筋内距加载端较近的荷载传感器测量值；R2为埋在钢筋内距自由端较近的荷载传感器测量值；F为拉拔力．图7所示为F、

图6 劈裂破坏试件典型照片

表1 劈裂破坏时各荷载传感器的测量值

图7 荷载与滑移量的关系曲线

R1和R2与加载端滑移量的关系曲线，3条曲线形状相近，变化规律相同．说明握裹层的径向受力性能是影响带肋钢筋黏结滑移本构关系的主要因素．

2 握裹层的约束作用

混凝土拉拔试件随着保护层约束程度的不同，通常发生劈裂破坏或者拔出破坏．发生劈裂破坏是由于钢筋横肋在钢筋与混凝土黏结界面处的挤压力使握裹层混凝土内部产生环向拉应力引起的．随着相对滑移的增大，该环向拉应力达到混凝土的抗拉强度时，混凝土在黏结界面处产生受拉裂缝．当保护层厚度较小时，会发生脆性的劈裂破坏．

对于混凝土保护层在黏结作用或钢筋锈蚀作用下产生的劈裂破坏问题，众多学者采用了很多方法进行分析．其中，Tepfers[7]首先对该问题作了初步的理论研究，研究中分别假定混凝土处于弹性状态、部分开裂状态(无黏聚力作用)和完全塑性状态，采用弹性力学厚壁圆筒理论对此问题进行了求解．根据混凝土断裂力学理论，混凝土开裂后仍然存在阻裂作用．因此文献[8-9]通过考虑裂缝间的黏聚力改进了开裂厚壁圆筒模型．图8为考虑裂缝间黏聚力的厚壁圆筒模型分析示意图，混凝土保护层分为两层：内层的开裂层和外层的弹性层．沿直径切开混凝土保护层，取隔离体列平衡方程可得径向压力和混凝土保护层周向应力的关系：

(1)

式中：σ和σφ分别是内层开裂混凝土和外层未开裂混凝土的周向应力．其中弹性未开裂层的周向应力可由裂缝尖端处应力边界条件求得，在裂缝尖端处有σφ=ft，根据受内压作用厚壁圆筒的弹性解可得周向应力为

(2)

对于内层开裂层，任一半径ρ处的周向伸长包括裂缝的宽度和裂缝间黏聚力引起的弹性伸长，可以采用下式计算：

(3)

式中：Ec为混凝土的弹性模量；n为径向裂缝的条数；w为单条裂缝的宽度．

图8 考虑裂缝间黏聚力的厚壁圆筒模型分析示意图

Fig.8 Schematic of thick-walled circular tube model considering cohesive force between cracks

利用式(3)计算裂缝间黏聚力还需要周向伸长Δφ和混凝土软化本构关系．本文采用文献[8]提出的周向伸长假定：

(4)

本文采用Petersson提出的双线性软化本构关系[10]，其数学表达式为

(5)

式中：σs=ft/3；ws=0.8Gf/ft；w0=3.6Gf/ft；Gf为混凝土的断裂能．由式(1)～(5)可以计算出混凝土握裹层的最大径向压力．

假设混凝土握裹层径向压力沿黏结面均匀分布，则径向压力可根据试验结果按下式计算：

(6)

式中：r为钢筋的半径；b为黏结段长度．考虑到钢筋内的微型荷载传感器实际测量的是包括黏结段和两端非黏结段握裹层的约束作用，故引入5/6的修正系数．该系数为黏结长度和起约束作用握裹层总长度的比值．图9为模型的预测值和本文试验结果的对比，图中pmax为保护层能够提供的最大径向压力．从图中可知，考虑裂缝间黏聚力的厚壁圆筒模型预测值与试验结果吻合较好．

图9 pmax的试验值与模型预测值对比

图10为试件劈裂破坏时混凝土握裹层径向压力合力作用点位置和保护层厚度的关系，α为握裹层径向压力合力作用点到加载端微型荷载传感器的距离与两个微型荷载传感器之间距离的比值．从图中可以看出，握裹层径向压力合力作用点随着保护层厚度的增加不断由加载端向自由端移动．α等于0.5时，径向压力合力作用在锚固段的中点．保护层厚度为34.5 mm时，α接近0.5，说明握裹层径向压力沿锚固段分布比较均匀，此时试件的破坏比较接近静水压力引起的劈裂破坏．保护层厚度为24.5 mm和48.5 mm时，握裹层径向压力合力作用点偏离了钢筋锚固段中点位置，这说明其径向压力沿锚固段分布不均匀．

在劈裂破坏时，由于钢筋和混凝土已经产生足够大的相对滑移，化学胶着力已经不存在，此时变形钢筋的黏结锚固作用只包含机械咬合作用和摩擦作用．由机械咬合作用产生的黏结应力沿锚固段的分布与握裹层径向压力的分布和钢筋肋前有效角相关．在锚固长度为5倍钢筋直径的情况下可以认为钢筋肋前有效角沿锚固段的变化很小，因此由机械咬合作用产生的黏结应力沿锚固段的分布与径向压力的分布相同．摩擦力等于径向压力乘以摩擦因数，所以由摩擦作用产生的黏结应力沿锚固段的分布也与径向压力的分布相同．从而总体的黏结应力的分布和径向压力的分布相同．因此，劈裂破坏时，黏结应力沿锚固段的分布受保护层厚度的影响，保护层适中时，黏结应力分布比较均匀；当保护层厚度过大或者过小时，黏结应力分布变得不均匀．从图10中可以看出，保护层厚度较小时，握裹层径向压力合力作用点距离加载端较近；当保护层厚度较大时，握裹层径向压力合力作用点距离自由端较近．保护层厚度较小时，劈裂破坏时加载端钢筋和混凝土的相对滑移量较小，相对滑移量自加载端向自由端递减．由于相对滑移量较小，距离加载端较远的混凝土握裹层还没有充分发挥约束作用便发生了脆性破坏；随着保护层厚度的增大，劈裂破坏时钢筋和混凝土的相对滑移量增大，然而握裹层的刚度比较大，在劈裂破坏时，距离加载端较近的混凝土握裹层由于相对滑移量过大，部分握裹层混凝土已经退出工作，不能再提供径向的约束作用．因此，随着保护层厚度的增加，握裹层径向压力合力作用点自加载端向自由端移动．

图10 劈裂破坏时α与c的关系

3 肋前有效角

混凝土中钢筋横肋传力机理如图11所示．随着钢筋和混凝土相对滑移的增加，挤碎的混凝土会在钢筋肋前形成一个新的斜面．该斜面与钢筋轴线的夹角随肋前混凝土挤碎区的发展而不断变化．钢筋肋前承受的平行于斜面和垂直斜面的力可分别表示为

Fn=σnAr

(7)

μFn=μσnAr

(8)

式中：Ar为锚固段所有横肋前斜面的面积和；μ为钢筋滑移过程中的摩擦因数．根据图12可以分别建立钢筋轴向和径向的平衡方程如下：

F=μFncosβ+Fnsinβ

(9)

2πrbp=Fncosβ-μFnsinβ

(10)

联立式(9)和(10)得

(11)

其中τ=F/2πrb．钢材表面容易发生不同程度的锈蚀，导致钢材和混凝土的摩擦因数取值范围较大．Ldun等[11]通过试验测定了砂浆和钢的摩擦因数，取值在0.503～0.627，平均值为0.56；Cairns等[12]通过试验测定混凝土和钢材的摩擦因数在0.5左右．钢筋滑移过程中不仅存在钢筋和混凝土间的摩擦作用，还包括钢筋横肋前挤碎的混凝土与握裹层混凝土之间的摩擦．显然，这两种摩擦作用的摩擦因数是不同的，然而由于两种摩擦作用的强弱关系难以确定，只能根据其摩擦因数的取值综合确定钢筋黏结滑移过程中的摩擦因数．综合考虑两种摩擦作用的摩擦因数，文献[9]建议μ取值范围为0.4～0.5．为简化分析，本文中μ取0.45．

图11 钢筋横肋传力示意图

根据试验测得的拉拔力和握裹层的径向压力，由式(6)和(11)可以得到整个劈裂过程中β的变化规律，如图12所示．从图中可以看出，随着拉拔力的增大，钢筋肋前有效角逐渐减小，说明机械咬合作用的效率不断降低．这是因为一方面随着钢筋和混凝土相对滑移的增大，混凝土握裹层径向位移增大，导致钢筋横肋和混凝土的作用点上移，钢筋横肋本身的有效角变小；另一方面随着拉拔力F的增大，肋前混凝土发生局部挤碎，挤碎的混凝土在钢筋横肋前堆积减小了有效角(见图12)．

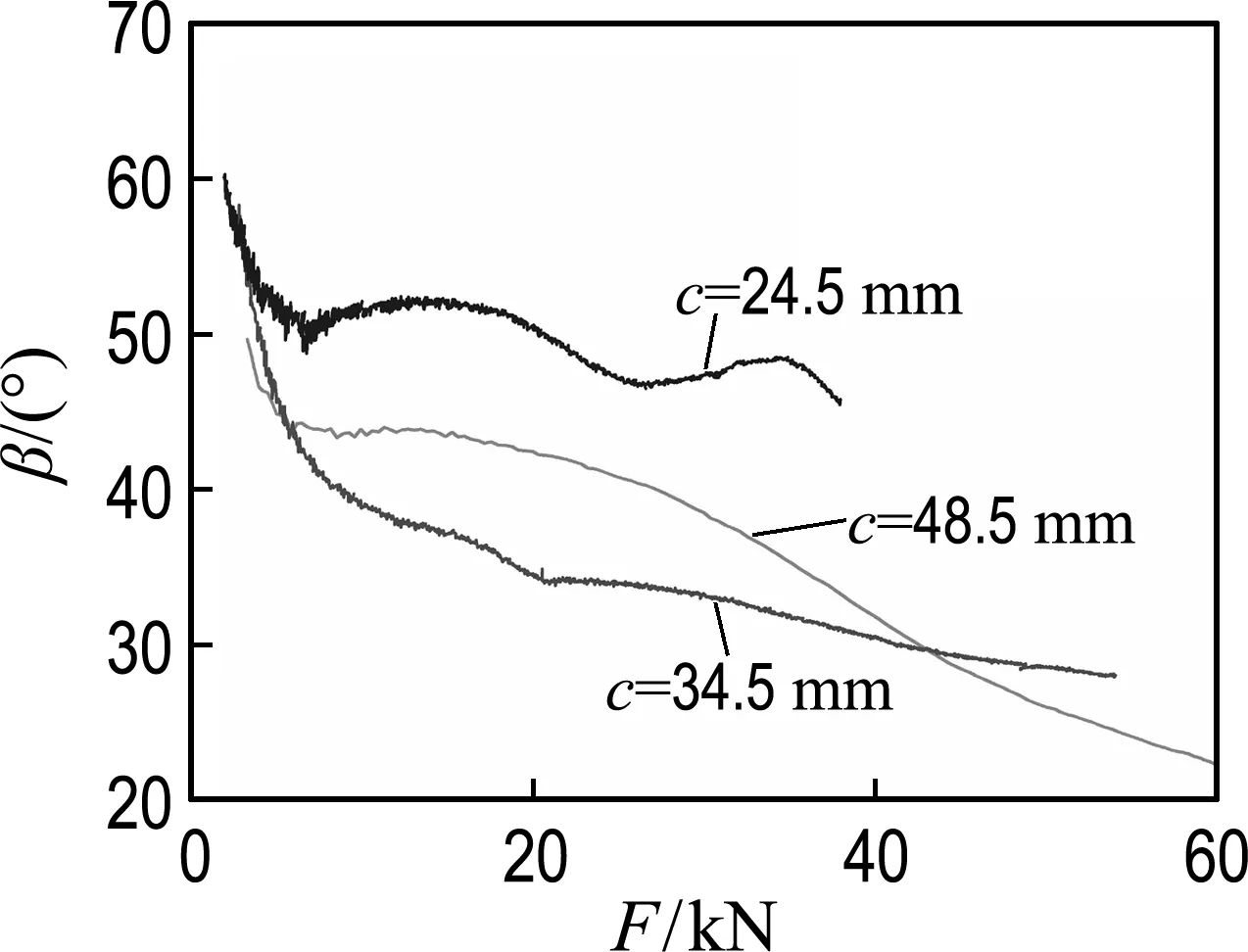
图12 劈裂破坏过程中β与F的关系

图13(a)给出了加载初始时刻，肋前有效角β与保护层厚度的关系．由图可知，β随着保护层厚度的增加而减小．保护层厚度越大，其径向刚度就越大，在相同滑移量下，机械咬合作用和摩擦作用就越强．加载初期，除了机械咬合作用和摩擦作用外，还存在化学胶着力，而化学胶着力一般与保护层厚度没有关系．这就导致，加载初期，保护层厚度越大，化学胶着力占全部抗拉拔力的比重越小；相反，保护层越薄，其化学胶着力在总的抗拉拔力中占的比重越大．推导式(11)时黏结应力中不包含化学胶着力，而加载初期测量的黏结应力中包含化学胶着力，此时的黏结应力大于由于机械咬合作用和摩擦作用引起的黏结应力．因此由式(11)计算的β偏大，且保护层厚度越小，偏大得越多；保护层厚度越大，偏大得越少．理论上，β的初始值只与钢筋的几何形状有关，也就是说不同保护层厚度情况下，β的初始值是相同的．但是化学胶着力的存在使得计算值偏离真实的钢筋肋前有效角，保护层厚度越大偏离的越小，计算值越接近真实的钢筋肋前有效角．

(a) 加载初期

(b) 劈裂破坏

图13 加载初期和劈裂破坏时β与c的关系

Fig.13 Relationship betweenβandcat the initial loading stage and splitting bond failure process

劈裂破坏时，Lutz等[1]认为钢筋肋前混凝土挤碎后形成的新滑移面与钢筋轴线的夹角在30°～40°；Hadje-Ghaffari等[13]通过对比普通钢筋和环氧树脂涂层钢筋的极限黏结强度，也得到夹角的上限在30°～40°；Choi等[9]通过有限元分析，建议夹角限定在25°～35°．图13(b)为根据本文试验结果计算得到的β，取值范围在21°～44°．本文确定β时，采用的是实测混凝土握裹层的径向压力和黏结应力，因此结果较为准确；而在其他文献中，往往通过有限元方法或者理论模型计算混凝土握裹层的径向压力，然后结合实测的黏结应力计算β．因此，本文得到的β取值范围与文献中的结果存在一定差异．劈裂破坏时，β随着保护层厚度的增加而减小．原因是，保护层越厚，劈裂时混凝土握裹层的约束作用越强，钢筋肋前混凝土挤碎得越多，导致钢筋横肋前有效角变小．

4 结 论

(1)对于带肋钢筋，在整个黏结滑移过程中黏结应力和混凝土握裹层径向压力成正比，二者与滑移量的关系曲线形状相似．说明混凝土握裹层的径向受力性能是影响带肋钢筋黏结滑移本构的主要因素．

(2)在锚固长度为5倍钢筋直径的情况下，带肋钢筋的黏结应力沿锚固段分布受保护层厚度的影响．保护层厚度过小或者过大都会导致带肋钢筋的黏结应力沿锚固段分布不均匀．保护层厚度过小时，锚固段前部的黏结应力大于锚固段后部的黏结应力；保护层过厚时，锚固段前部的黏结应力小于锚固段后部的黏结应力．

(3)在整个黏结滑移过程中，一方面随着混凝土握裹层的约束作用不断增大，钢筋横肋前混凝土被挤碎并在肋前堆积；另一方面随着混凝土握裹层径向位移不断增大，钢筋横肋和混凝土相互作用的位置上移，钢筋横肋本身的有效角变小．以上两方面共同作用导致在钢筋黏结滑移过程中，肋前有效角β不断减小，带肋钢筋的机械咬合作用效率不断降低．在劈裂破坏时，由试验结果确定β的取值范围为21°～44°，且随着保护层厚度的增加β不断变小．

[1] Lutz L A, Gergely P. Mechanics of bond and slip of deformed bars in concrete [J]. ACI Journal, 1967, 64(11):711-721.

[2] Goto Yukimasa. Cracks formed in concrete around deformed tension bars [J]. American Concrete Institute Journal & Proceedings, 1971, 68(4):244-251.

[3] Eligehausen R, Popov E P, Bertero V V. Local bond stress-slip relationships of deformed bars under generalized excitations [C] // Proceedings of the 7th European Conference on Earthquake Engineering. Athens:The Technical Chamber of Greece, 1982:69-80.

[4] 宋玉普,赵国藩. 钢筋与混凝土间的粘结滑移性能研究[J]. 大连工学院学报, 1987, 26(2):93-100.

SONG Yu-pu, ZHAO Guo-fan. Study of bond-slip property between steel bars and the concrete [J]. Journal of Dalian Institute of Technology, 1987, 26(2):93-100. (in Chinese)

[5] 徐有邻,沈文都,汪 洪. 钢筋砼粘结锚固性能的试验研究[J]. 建筑结构学报, 1994, 15(3):26-37.

XU You-lin, SHEN Wen-du, WANG Hong. An experimental study of bond-anchorage properties of bars in concrete [J]. Journal of Building Structures, 1994, 15(3):26-37. (in Chinese)

[6] Clark L A, Williamson S J. Pressure required to cause cover cracking of concrete due to reinforcement corrosion [J]. Magazine of Concrete Research, 2000, 52(6):455-467.

[7] Tepfers R. Cracking of concrete cover along anchored deformed reinforcing bars [J]. Magazine of Concrete Research, 1979, 31(106):3-12.

[8] 徐 峰. 复杂应力状态下钢筋与混凝土的粘结性能[D]. 大连:大连理工大学, 2012.

XU Feng. Bond performance of reinforcement in concrete subjected to complex lateral pressure [D]. Dalian:Dalian University of Technology, 2012. (in Chinese)

[9] Choi O C, Lee W S. Interfacial bond analysis of deformed bars to concrete [J]. ACI Structural Journal, 2002, 99(6):750-756.

[10] Petersson P-E. Crack growth and development of fracture zones in plain concrete and similar materials: Report TVBM 1006 [R]. Sweden:Division of Building Materials, LTH, Lund University, 1981.

[11] Ldun E K, Darwin D. Bond of epoxy-coated reinforcement:coefficient of friction and rib face angle [J]. ACI Structural Journal, 1999, 96(4):609-616.

[12] Cairns J, Abdullah R. Fundamental tests on the effect of an epoxy coating on bond strength [J]. ACI Materials Journal, 1994, 91(4):331-338.

[13] Hadje-Ghaffari H, Darwin D, McCabe S L. Effect of epoxy coating on bond of reinforcing steel to concrete [R]. Kansas: The University of Kansas Center for Research, Inc., 1991.

Experimental study of radial pressure of concrete cover on bond behavior of ribbed steel bars

WANG Li-cheng*, LI Long-long, LIANG Yong-qin

( State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China )

Bond behavior between concrete and ribbed steel bars is governed by interlocking force between concrete and transverse ribs. The radial pressure of concrete cover is an essential condition that studies the interaction between the transverse ribs of ribbed steel bars and concrete. Pull-out tests were carried out to measure the radial pressure of ribbed steel bars acted by concrete cover for the case of splitting bond failure. In this test two micro-load transducers embedded in the grooved steel bar were positioned to measure the radial pressure of concrete cover. The pull-out tests of a total of six specimens were conducted to obtain the confinement with different cover thicknesses. In the experiment, it is found that during the process of splitting bond failure the effective rib face angle gradually decreases and the bond stress is directly proportional to the radial pressure of concrete cover. When approaching to the splitting bond failure, the effective rib face angle is inversely proportional to the thickness of concrete cover. The distribution of bond stress along anchorage length of steel bar is influenced by the thickness of concrete cover. The appropriate thickness of concrete cover will lead to a uniform distribution of bond stress. Additionally, the maximum radial pressure of concrete cover measured experimentally is in good agreement with that predicted by thick-wall cylinder model, which takes the cohesive force of cracks into account.

ribbed steel bars;concrete cover; confinement; splitting bond failure; mechanical interaction

2016-04-15；

2016-09-25．

“九七三”国家重点基础研究发展计划资助项目(2015CB057703)；国家自然科学基金资助项目(51378090).

王立成*(1975-)，男，博士，教授，博士生导师，E-mail:wanglicheng2000@163.com.

1000-8608(2016)06-0608-08

TU313；O331

A

10.7511/dllgxb201606008