城市轨道交通合理规模综合计算模型研究

陈 坚，李 武，赵翰林，吴改选

CHEN Jian1, LI Wu2, ZHAO Han-lin2, WU Gai-xuan3

（1.重庆交通大学 交通运输学院，重庆 400074；2.重庆交通大学 山地城市交通系统与安全重庆市重点实验室，重庆 400074；3.四川省交通运输厅 交通勘察设计研究院，四川 成都 610017）

(1.School of Traffic and Transportation， Chongqing Jiaotong University， Chongqing 400074， China； 2.Chongqing Key Lab of Traffic System & Safety in Mountain Cities， Chongqing Jiaotong University， Chongqing 400074， China； 3.Communication Survey & Design Institute， Department of Transportation of Sichuan Province， Chengdu 610017， Sichuan， China)

城市轨道交通合理规模综合计算模型研究

陈 坚1，李 武2，赵翰林2，吴改选3

CHEN Jian1, LI Wu2, ZHAO Han-lin2, WU Gai-xuan3

（1.重庆交通大学 交通运输学院，重庆 400074；2.重庆交通大学 山地城市交通系统与安全重庆市重点实验室，重庆 400074；3.四川省交通运输厅 交通勘察设计研究院，四川 成都 610017）

(1.School of Traffic and Transportation， Chongqing Jiaotong University， Chongqing 400074， China； 2.Chongqing Key Lab of Traffic System & Safety in Mountain Cities， Chongqing Jiaotong University， Chongqing 400074， China； 3.Communication Survey & Design Institute， Department of Transportation of Sichuan Province， Chengdu 610017， Sichuan， China)

针对目前城市轨道交通线网规模预测存在的问题，即不同预测方法的预测结果相差较大，操作性和解释性不强，提出城市轨道交通合理规模的概念，从宏观和微观层面分析城市轨道交通合理规模的影响因素。在分析服务水平法、交通需求分析法和回归分析法的适用性及优缺点的基础上，应用几何平均数改进标准化处理过程，计算各预测方法结果的信息熵，并根据熵的大小推导各方法权重系数，从而建立基于改进熵权系数的城市轨道交通合理规模综合计算模型。以重庆市为例，应用该模型得出 2020 年重庆市轨道交通合理规模值。

城市轨道交通；线网规模；信息熵；计算模型；服务水平

1　概述

我国传统城市公共交通体系在日益增长的城市人口和不断扩大的城市规模背景下，已经无法满足快速增长的交通出行需求，建设以城市轨道交通为主体的多元化城市公共交通体系已成为社会各界共识。城市轨道交通具有建设成本高、建设周期长、建设难度高等特点，因而科学确定轨道交通线网合理规模成为轨道交通建设的重要内容之一。

轨道交通规模主要通过线网密度及对外服务水平来界定，其大小应与交通系统所提供的交通服务相匹配，是交通系统服务能力的重要体现。服务水平越高，要求城市轨道交通线网的规模越大，但由于受人口规模和经济能力的制约，城市轨道交通线网的规模具有相应的阈值。在一定的经济水平及资源条件约束下，合理的城市轨道交通规模既能够满足中长期的交通需求，又能有一定的引领带动城市发展的作用，它是综合考虑交通系统服务水平和轨道交通分担率下的城市轨道交通线网总长度。

近年来，国内外学者对城市轨道交通线网规模进行了探索，顾保南等[1]使用几何分析法、运输强度分析法和类比分析法对轨道交通网络规模进行估算；金健等[2]探讨基于梯度效应、弹性效应、平衡效应和综合效应的轨道交通线网规模计算框架；安学武等[3]从溢出需求角度建立线网规模负荷强度计算法；鲁放等[4]以综合效率最优为目标计算城市轨道交通线网规模；王智鹏等[5]在“溢出+转移”城市轨道交通客流预测基础上进行线网规模计算；张杰[6]、张云等[7]研究嘉兴、哈尔滨轨道交通线网建设规模与 GDP 总量、人口数等的关系；Gergek H等[8]建议采用层次分析法对多个可供选择的轨道交通网络规模方案进行遴选；Chakrobort P[9]运用遗传算法计算轨道交通网络的合理规模。目前城市轨道交通线网规模计算方法较多，但还没有提出合理规模的概念，而且同一个城市使用不同方法计算出的结果相差较大。为此，基于熵权建立多种方法的综合取值模型，从而避免单一方法的局限性。

城市轨道交通合理规模受外部影响较大，并且随着城市规模的扩大，影响因素呈增多趋势。根据每个因素的作用效果差异，将其划分为宏观影响因素和微观影响因素。

（1）宏观影响因素。城市轨道交通合理规模受到国家政策，城市形态、规模及布局、城市 GDP、城市基础设施投资比例等宏观因素的影响[10]。首先，轨道交通建设资金需求量大，需要国家财政扶持，而大力推行公共交通优先发展是我国的基本国策。其次，城市规模与城市交通需求量有着最为直接的作用关系，可以对城市轨道交通的需求程度造成深刻影响，从而决定是否需要建设发展城市轨道交通，并确定建设规模的大小。再者，城市地理形态和城市业态布局的差异性同时决定市民出行的空间分布，由此，城市轨道交通线网的空间形态、布局及结构也随之确定。最后，从建设资金角度来看，城市国内生产总值是实现轨道交通建设的经济基础，它与城市基础设施投资比例共同对城市轨道交通网络建设规模进行制约。

（2）微观影响因素。城市轨道交通合理规模的微观影响因素包括居民出行方式选择行为、轨道交通价格、轨道交通服务质量等。城市交通需求是指出行者在出行过程中对各类交通基础设施的需要程度，特别是对城市公共交通的需求程度，这是确定线网合理规模的首要因素。

2　基于熵权的城市轨道交通合理规模综合计算模型

目前常用的确定城市轨道交通规模的方法中，服务水平法、交通需求分析法和回归分析法理论基础比较完整，适用范围相对较广，可操作性及可靠性相对较高，因而在这 3 种方法的基础上，应用熵权模型，对不同方法计算的规模进行加权，从而得出城市轨道交通合理规模的综合推荐结果。

2.1服务水平法

服务水平法的实质是将城市规划区划分为中心区和中心外围区，根据交通需求强度在不同区域的差异，利用各自线网密度指标按下式推算城市轨道交通线网的规模。但是，该方法存在类比依据不足、置信度不高的缺陷。服务水平法计算线网规模的公式为

式中：L1为服务水平法下的线网合理规模，km；S1为城市中心区面积，km2；M1为城市中心区线网密度，km/km2；S2为城市中心外围区面积，km2；M2为城市中心外围区线网密度，km/km2。

2.2交通需求分析法

交通需求分析法是将预测年的城市各出行方式的总量预测出来，再按照预先确定的城市轨道交通线网密度，以及各线路需分配的出行量百分比确定线网规模，但该方法的计算数据涉及局部主观推算和假设。交通需求分析法计算线网规模的公式为

式中：L2为交通需求分析法下的线网合理规模，km；Q 为预测年城市交通出行总量，万人次/d；α 为预测年公交出行比例，与城市公交优先政策相关，建议取值范围为 0.3～0.6；β 为城市轨道交通出行占公交出行的比例，取值在 0.5 左右；θ 为城市轨道交通换乘系数，根据各城市的站点布设情况和直达程度进行不同取值；I 为轨道交通线网负荷强度，万人次/(km · d)。

预测年城市交通出行总量 Q 可以表示为城市人口总量和出行强度的乘积，即

式中：ms为实际居住人口，万人；ns为实际居住人口的出行强度，次/d；mz为流动人口，万人；nz为流动人口的出行强度，次/d。城市结构、经济发展水平、交通设施的完善程度等方面是居民出行强度的主要影响因素。

2.3回归分析法

选取线网规模、城市交通出行量等影响因素进行回归分析，从而推导出线网规模与各影响因素的函数关系式。再代入各个影响因素在预测年的估计值，计算出规划城市在预测年的线网合理规模。但该方法存在难以寻找合适的拟合样本量的问题，而且线网规模的部分影响因素不易定量化。

假设城市轨道交通线网规模与城市交通出行量、城市都市区面积之间的函数关系为

式中：L3为回归分析法下的城市轨道交通线网合理规模，km；R 为城市交通出行量，万人次/d；S 为城市面积，km2；b0，b1，b2为回归系数。

由 ⑷ 式可知，城市轨道交通线网合理规模的自然对数与城市交通出行量的自然对数、城市都市区面积的自然对数满足二元线性关系，即

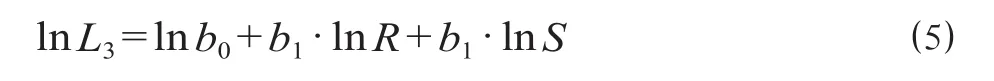
对世界上 48 个城市轨道交通系统的相关统计数据进行二元线性回归[10]，所得回归系数为：

基于上述分析，通过回归分析法得到的城市轨道交通线网规模计算公式为

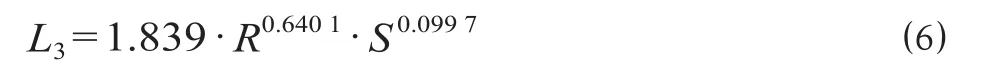
式中：L3为回归分析法下的城市轨道交通线网合理规模，km；R 为城市交通出行量，万人次/d；S 为城市面积，km2。

2.4基于熵权的综合计算模型

由于服务水平法、交通需求分析法和回归分析法3种方法各有优势和不足，因此，在城市轨道交通线网合理规模确定过程中，通过对不同计算方法赋予不同权重，从而避免采用单一方法的解释性和说服力不足的问题，即

式中：Li为第 i 种方法的计算结果，km；wi表示第 i 种计算方法的权重系数。

权重系数表示各计算方法在计算过程中所占的重要程度。鉴于不同计算方法包含具有差异的信息效用价值，为此采用熵权法确定各计算方法的权重系数。假定对同一研究对象有 i 种计算方法可以同时得出计算结果，利用熵权法确定不同计算方法权重系数的步骤如下。

步骤 1：计算结果标准化处理。考虑到传统的标准化处理模型在某一方法的预测结果为所有方法预测结果的最大值或最小值时，该方法的权重系数为零，即忽略该种预测方法对结果的影响，这与实际决策过程不符。因此，提出运用几何平均数的改进标准化处理方法，从而避免某一方法的计算结果标准化后出现零的情况，即

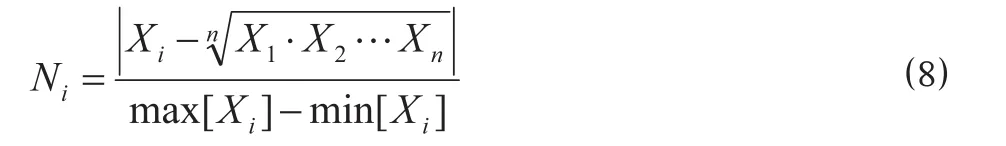
式中：Xi为初始计算结果；Ni为标准化处理后得到的计算结果，Ni∈ (0，1)。

步骤 2：计算第 i 种预测方法的熵[11-12]。根据信息论可知，第 i 种决策办法的熵 Hi为

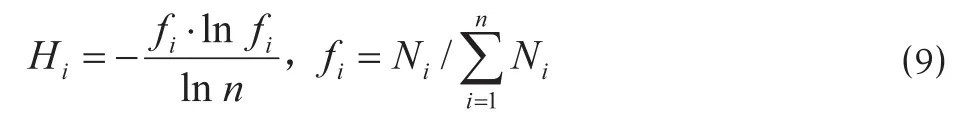
式中：fi为不同方法计算结果标准化后的比例系数。

当 Ni为 0 时，令 fi为 0。

步骤 3：计算第 i 种方法的熵权系数。定义第 i种方法的权重系数 wi为

则所有方法计算结果的权重向量 W 为

3　实例分析

结合重庆市 2020 年城乡总体规划，运用基于熵权的综合计算模型，对 2020 年重庆市城市轨道交通线网合理规模进行分析。

（1）服务水平法计算结果。根据《重庆市城乡总体规划 (2007—2020 年)》(2011 年修订)，重庆市城镇都市区城镇和中心城区城镇建设用地规模如表 1 所示。

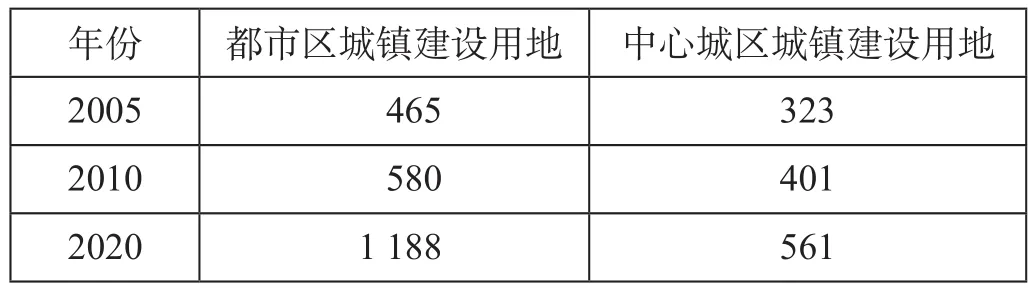
表1　重庆市用地规模 km2

综合考虑重庆市城市发展布局、公共交通基础设施配套，以及居民出行行为情况，重庆市 2020年轨道交通线网密度中心区取 0.7 km/km2，中心外围区取 0.25 km/km2。因此，根据公式 ⑴，结合表 1 数据，可以求出重庆市 2020 年中心城区范围、中心外围区的合理线网规模分别为

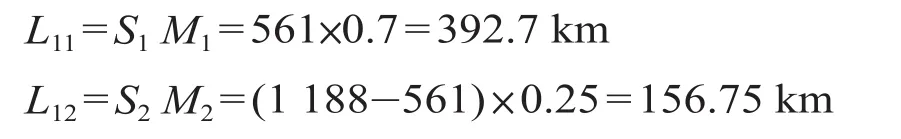
依据服务水平分析法得到城市轨道交通线网的合理规模为

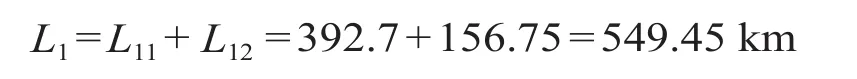
（2）交通需求分析法计算结果。到 2020 年，重庆市常住人口约为 1 240 万人，市内流动人口将达到 436.73 万人。常住人口人均出行强度 ns接近2.5～3.0 次/d，在此取 2.75。流动人口多为务工人员，人均出行强度 nz按 2.5 计。轨道交通换乘系数 θ 取 1.3。公共交通出行在居民出行中的比例 α 将超过 47%，轨道交通方式出行在公共交通出行中所占比例 β 将在 45% 以上，在此取 α = 47%，β = 45%。根据国内外部分大城市线网负荷强度[13]，结合重庆城市轨道线路发展情况，取 2020 年重庆市轨道交通日平均负荷强度 I 为 1.7 万人次/(km · d)。依据公式 ⑵ 和公式 ⑶，计算得出 2020 年重庆市城市交通出行总量为

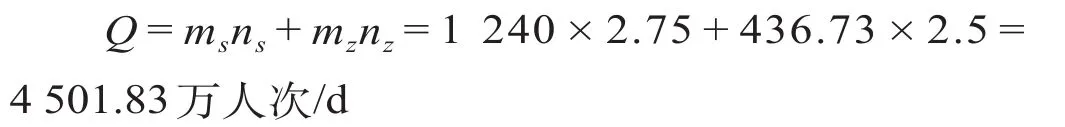
依据交通需求分析法得到城市轨道交通线网合理规模为

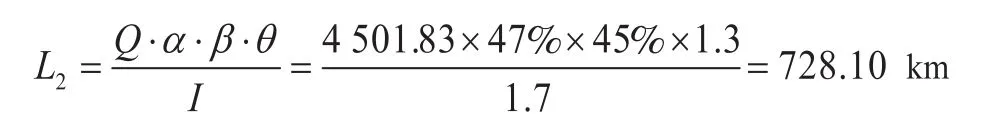
（3）回归分析法计算结果。2020 年重庆市主城区建成面积为 1 188 km2，相应城区内预测出的城市交通出行量为 1 709.57 万人次/d。依据回归分析法计算得到重庆市城市轨道交通线网合理规模为

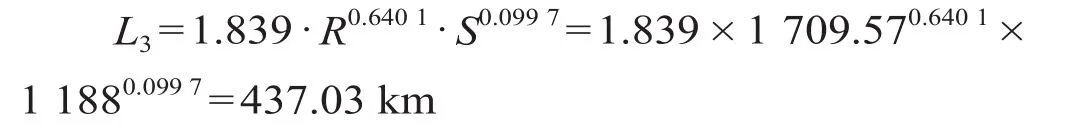
（4）综合计算模型结果。根据公式 ⑺—⑾，首先计算服务水平法、交通需求分析法和回归分析法的熵权系数如表 2 所示。

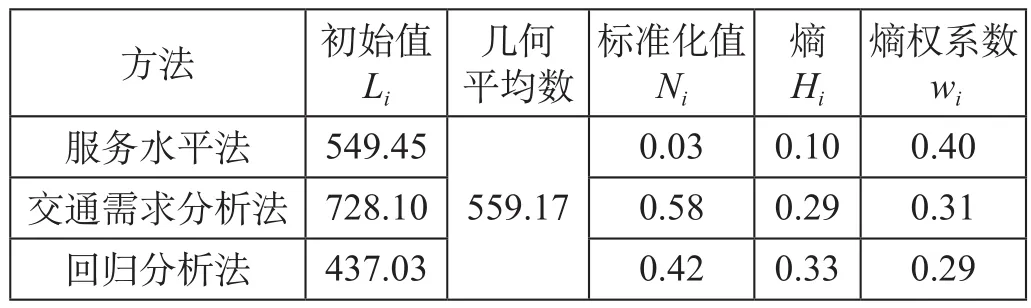
表2　不同计算方法的熵权系数

则权重向量 W = (0.40 0.31 0.29)，因而基于熵权模型综合计算得出的重庆市 2020 年的城市轨道交通线网的合理规模为

4　结束语

合理规模是城市轨道交通规划设计的关键参数，它直接决定城市轨道交通的投资及运营服务水平。通过梳理目前城市轨道交通规模的计算方法与模型，采用信息熵定量确定各方法权重，从而获得各种方法综合计算结果的思路。实例分析结果计算得出重庆市 2020 年城市轨道交通合理规模值为 571.90 km，比目前规划的 504.22 km 增加了13.42%。由于模型因素选择的差异性，综合预测结果还是存在一定的主观影响，因素的类别及定量计算将是模型改进的方向。

[1] 顾保南，叶霞飞，许 恺. 上海市中心城轨道交通网络规划合理规模研究[J]. 上海铁道大学学报，2000，21(10)：36-38. GU Bao-nan，YE Xia-fei，XU Kai. A Study on the Scale Length of the Network Plan of Shanghai Rapid Rail Transit[J]. Journal of Shanghai Tiedao University，2000，21(10)：36-38.

[2] 金 键，张殿业，郭孜政. 城市轨道交通合理规模机理及模型分析[J]. 铁道学报，2006，28(5)：16-19. JIN Jian，ZHANG Dian-ye，GUO Zi-zheng. Demand Mechanism Model Analysis of Rational Scale of Urban Rail Transit Network[J]. Journal of the China Railway Society，2006，28(5)：16-19.

[3] 安学武，杜殿虎，马超群，等. 基于溢出交通需求的城市轨道交通线网规模测算模型[J]. 交通运输工程学报，2008，8(3)：82-85. AN Xue-wu，DU Dian-hu，MA Chao-qun，et al. Computation Model of Network Scale for Urban Rail Transit based on Traffic Demand Overflow[J]. Journal of Traffic and Transportation Engineering，2008，8(3)：82-85.

[4] 鲁 放，韩宝明，李得伟. 基于综合效率的城市轨道交通网规模研究[J]. 综合运输，2009(8)：28-31. LU Fang， HAN Bao-ming，LI De-wei. Research on Scale of Urban Rail Transit based on Comprehensive Efficiency[J]. Comprehensive Transportation，2009(8)：28-31.

[5] 王智鹏，罗 霞. 综合交通系统条件下城市轨道交通线网规模测算[J]. 长安大学学报 (自然科学版)，2015，35(1)：193-197. WANG Zhi-peng，LUO Xia. Scale Calculating on Urban Rail Transit Network under the Condition of Comprehensive Transportation System[J]. Journal of Chang’an University (Natural Science Edition)，2015，35(1)：193-197.

[6] 张 杰. 中等规模城市轨道交通线网规划思路[J]. 都市快轨交通，2012，25(2)：32-35. ZHANG Jie. Ideas for Planning Urban Rail Transit Network for Medium-Sized Cities[J]. Urban Rapid Rail Transit，2012，25(2)：32-35.

[7] 张 云，徐慧智. 哈尔滨市近期轨道交通建设条件及规模探索[J]. 都市快轨交通，2011，24(4)：65-68. ZHANG Yun，XU Hui-zhi. Study on the Conditions and Scale of Subway Construction in Harbin City[J]. Urban Rapid Rail Transit，2011，24(4)：65-68.

[8] Gergek H，Kilinaaslan T，Karpak B. A Multiple Criteria Approach for the Evaluation of the Rail Transit Networks in Istanbul[J]. Transportation，2010，31(7)：23-28.

[9] Chakroborty P. Genetic Algorithms for Optimal Urban Transit Network Design Computer Aided Civil and Infrastructure Engineering [J]. 2003，18(3)：18-20.

[10] 周 强，秦菲菲，吴 戈. 基于 DEA 方法的城市轨道交通系统效率评价研究[J]. 铁道运输与经济，2014，36(2)：79-83. ZHOU Qiang，QIN Fei-fei，WU Ge. Study on Efficiency Evaluation of Urban Rail Transit System based on DEA[J]. Railway Transport and Economy，2014，36(2)：79-83.

[11] Verma A，Dhingra S. L. Suitability of Altemative Systems for Urban Mass Transport for Hidian Cities[J]. Transportion European，2011，25(6)：4-15.

[12] 于江霞，于景群，王选仓. 基于神经网络的公路网规模预测[J]. 长安大学学报 (自然科学版)，2006(1)：75-78. YU Jiang-xia，YU Jing-qun，WANG Xuan-cang. Highway Network Scale Prediction based on BP Neural Network[J]. Journal of Chang’an University (Natural Science Edition)，2006(1)：75-78.

[13] 陈 坚. 城市轨道交通概论[M]. 长沙：中南大学出版社，2014. CHEN Jian. Introduction to Urban Rail Transit[M]. Changsha：Central South University Press，2014.

责任编辑：金 颖

Study on Comprehensive Calculation Model of Reasonable Scale of Urban Rail Transit

Targeting with problems existing in current forecast of line-network scale of urban rail transit, such as different forecast method has great difference in forecast result and has less operability and explanation, this paper puts forward the concept of reasonable scale of urban rail transit, and analyzes the influence factors of the reasonable scale from macro-level and microlevel. Based on analyzing the applicability, advantages and disadvantages of service level method, traffic demand analysis and regression analysis, the standardization process is improved by using geometric mean, the information entropy of each forecast method result is calculated and the weight coefficient of each forecast method is derived according to the entropy value, thereby, the comprehensive calculation model of reasonable scale of urban rail transit based on improved entropy-weights coefficient is established. Taking Chongqing as an example, the reasonable scale value of urban rail transit in Chongqing in 2020 is achieved by using the calculation model.

Urban Rail Transit; Line-network Scale; Information Entropy; Calculation Model; Service Level

1003-1421(2016)02-0071-05

U121

A

10.16668/j.cnki.issn.1003-1421.2016.02.15

2015-10-13

国家自然科学基金(51308569)；重庆市教育委员会人文社会科学研究重点项目(14SKG03)；重庆市基础与前沿研究计划项目(cstc2013jcyjA30002)