基于 PCA-BP 神经网络的城市轨道交通线网方案评价研究

陈 光, 李珊珊，董 博

CHEN Guang, LI Shan-shan, DONG Bo

（华北理工大学 建筑工程学院，河北 唐山 063009）

(School of Construction Engineering， North China University of Science and Technology， Tangshan 063009，Hebei， China)

基于 PCA-BP 神经网络的城市轨道交通线网方案评价研究

陈 光, 李珊珊，董 博

CHEN Guang, LI Shan-shan, DONG Bo

（华北理工大学 建筑工程学院，河北 唐山 063009）

(School of Construction Engineering， North China University of Science and Technology， Tangshan 063009，Hebei， China)

建立 PCA-BP 神经网络的评价模型，将主成分分析法和 BP 神经网络算法引入评价过程，在利用主成分分析法降维同时能够最大程度保留初始信息的基础上，发挥 BP 神经网络解决非线性和复杂问题的优势，对线网布局方案进行评价。最后，通过实际案例分析，证明基于 PCA-BP 神经网络的评价方法适用于线网布局方案评价，是城市轨道交通线网方案的有效评价方法。

主成分分析法；BP 神经网络；线网方案评价

0　引言

在评价轨道交通线网的过程中，应综合考虑区域土地使用性质、人口分布、换乘站布置、居民出行的 OD 分布等多种因素，这些影响因素在一定程度上具有相关性，因而评价过程多存在复杂性和非线性[1]。常用的线网布局方案评价方法主要有层次分析-模糊综合评价、主成分分析法 (PCA)-BP 神经网络评价法、多元线性回归分析法等。

由于城市轨道交通线网方案评价指标的多样性、复杂性，在评价中应尽量减少指标数量，找出最具有代表性、对评价结果影响大的指标。主成分分析法能够有效地对各种复杂、多样的指标进行降维，实现采用较少的变量信息概括多个变量信息，从而大幅简化后续步骤的计算量[2]。BP 神经网络法能够很好地处理非线性问题，并且具有较高的容错性和抗干扰性，将实际的评价指标代入该网络进行训练，能够较为科学地对不同轨道线网方案进行评价[3]。因此，在对原始指标变量的降维处理过程中，采用主成分分析法以降低指标间的关联性。此外，为提高训练精度，对数量较少的指标变量进行筛选，并将其作为研究样本，以降低 BP 神经网络的输入复杂程度，提升训练精准度。

结合国内外学者及规划部门在轨道交通建设方面的理论和实践经验，综合考虑城市轨道交通的影响因素，在模型建立过程中以线网结构、运营效率、社会效益、城市发展和建设实施 5 个因素作为准则层，并以线网客流覆盖率等 25 个指标作为方案评价的指标体系[4]，其结构关系如图 1 所示。

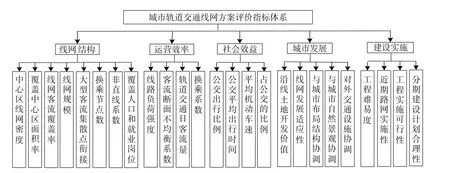
图1　准则层和指标体系的结构关系

1　城市轨道交通线网基本模型建立

1.1主成分分析法

基于 PCA 的基本思想，对指标体系中的指标进行降维。设定每个高层指标下包含若干个子指标，子指标的个数用 p 表示，分别为 X1，X2，…，Xp，将这些子指标设定为 1 组随机变量 X = (X1，X2，…，Xp)T，对 X 进行线性变化，得到原始变量的线性组合[5]为

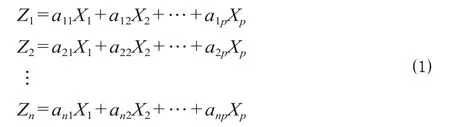
式中：Z1，Z2，…，Zn(n ＜ P) 为新变量指标。以方差 D (Zn) 为每个主成分提取信息量的度量指标，D (Zn) 的值越大，表明该指标所含有的信息量越大。假设向量 Z1满足公式 ⑵，在该模型中即可将 X 的第 1 主成分设定为 Z1，如果 Z1不能全面概括其包含的 p 个指标所反映的内容，则将 Z2设定为第 2 主成分；以此类推，即可找到能够较为充分反映指标信息的主成分。

1.2基于 PCA-BP 神经网络的评价模型

BP 神经网络是一种包括输入层、输出层和若干个隐含层在内的多层前向型网络[6]。在训练过程中，通过向神经网络输入样本信息，经过隐含层进行计算，再输送到输出节点。如果出现期望与实际输出结果不相吻合，将会出现误差，此误差将会逆向传递，即由输出层向输入层方向传递[7]。在此过程中，每个神经元都会分到一部分误差。一般情况下，在 BP 神经网络中通过 3 层就可以完成任意 n 维到 m 维的映射[8]。在训练过程中，将 BP 神经网络划分为 3 个层次，通过对指标变量个数的筛选，可以确定输入层节点个数。在实例分析中，最终要得到的结果是轨道交通线网的评价得分，可以将其作为最终的输出层，而且在模型中的表现形式为单个神经元。基于上述设置，构建基于 PCA-BP 神经网络的评价模型如图 2 所示。

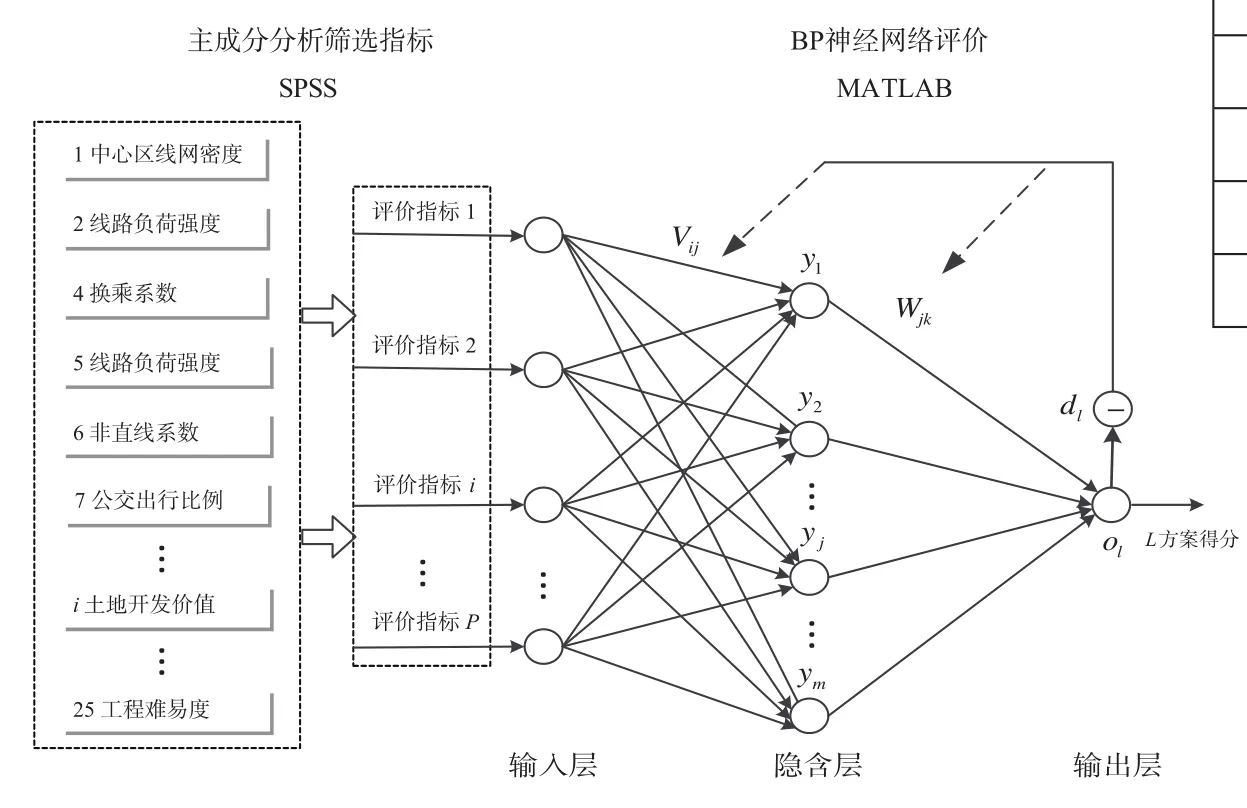
图2　PCA-BP 神经网络评价模型

在 PCA-BP 神经网络评价模型中，对选定的 25个评价指标进行主成分分析，获取其特征信息，神经网络的输入变量采用筛选得到的 p 个指标，以提高训练的准确度并降低 BP 神经网络训练难度[9]。

2　实例分析

2.1主成分分析法指标筛选

借助SPSS分别对某城市线网结构、运营效率、社会效益、城市发展、建设实施 5 类指标进行主成分分析，以线网结构为例对指标进行筛选。

（1）建立轨道线网指标的相关系数矩阵。采用SPSS软件辅助完成轨道线网指标的样本标准化，得到描述城市轨道交通线网方案线网结构的系数矩阵。通过该矩阵可知，换乘节点数与中心区线网密度之间有相关关系，应对其选择以减少相互影响的重叠信息。

（2）计算特征值及累计贡献率。各个指标相关系数矩阵的特征值和成分贡献率如表 1 所示，其中第 1、第 2、第 3、第 4 主成分所映射的指标样本信息主要依靠累计贡献率达 85% 的原则来确定。

表1　特征值及累计贡献率 %

（3）根据成分矩阵确定关键指标。各个指标变量及其对应主成分的相关系数通过成分矩阵的每一列荷载值来显示，城市轨道交通线网结构指标成分矩阵如表 2 所示。系数值愈大，则该指标变量能够反映的主成分信息也就愈多。因此，每一列中系数最大的值即为其关键指标。

表2　城市轨道交通线网结构指标成分矩阵

在表 2 中，确定第 1 主成分的关键指标应为表2 中最大数值对应的指标 (0.890)，即非直线系数；同理可知，第 2、第 3、第 4 主成分的关键指标为中心区线网密度、与大型客流集散点衔接数量、线网规模。通过上述方法，可以得到 1 组能够反映原有样本的指标集，而该指标集能够反映充足的信息量。

以相同的方法分别对运营效率指标、社会效益指标、城市发展指标及建设实施指标进行计算，即可得到如图 3 所示的该市轨道交通线网方案评价指标体系。

2.2轨道交通线网方案的 BP 神经网络评价

（1）确定样本及期望输出。在应用 PCA 法筛选出线网方案的关键评价指标后，将筛选出的关键指标作为 BP 神经网络的输入变量。结合实际情况，聘请专家组对图 3 中的 15 个轨道交通线网指标进行分值标定，并将所对应的专家标定数据作为训练样本的输入变量代入 BP 神经网络进行计算。通过对专家组打分结果和 BP 神经网络的计算结果进行对比，来验证 BP 神经网络法评价城市轨道交通线网的准确性。

对 15 个指标的权重进行计算，得到期望输出为

T = (0.77，0.78，0.80，0.82，0.81，0.81，0.80，0.82，0.81，0.82，0.81，0.80，0.85，0.85，0.84)

（2）确定隐含层节点数量。隐含层神经元数目的确定是一个复杂的过程，需要根据设计者的经验和大量的实验来确定。根据经验公式，其中 h 为隐含层神经元个数，m 为输入层神经元个数，n 为输出层神经元个数，a 为 [1，10] 之间的常数。研究的输入层神经元个数为 15，输出层神经元个数为 1，确定 BP 神经网络的隐含层神经元数量 h 的取值范围为 [5，14]，运用 Matlab 计算工具，分析隐含层节点数为 [5，14] 的神经网络误差，结果如表 3 所示。根据表 3 可知，隐含层节点个数为 7 时，误差最小，因而最终确定隐含层节点个数为 7 个。

表3　不同隐含层 BP 神经网络误差对比情况

（3）网络测试。采用测试样本 (选用实际测得的 3 组数据) 对隐含层节点数为 7 的 BP 神经网络进行模拟测试，达到最小误差时，只需要 5 步，网络输出与期望输出的模拟关系如图 4 所示。图 4 中 T表示期望值，y 表示实际输出值。上述仿真结果说明网络的期望值 T 与实际输出值 y 差距很小，所设定的 BP 神经网络是可行的，在进行城市轨道交通线网方案评价中，可以直接将各指标变量输入进行计算。

2.3实证分析

以该市轨道交通线网规划建设为研究基础，根据人口分布、交通结构及现状公交线路设置等因素，规划 3 种不同的轨道交通线网方案如下。方案1：共有 5 条线路，其中 3 条纵向，2 条横向，线路总长度约为 81 km，线路结构如图 5 所示。方案 2：共有 5 条线路，2 条横向，2 条横向，并且设置 1 条环线，线路总长度约为 95 km，线路结构如图 6 所示。

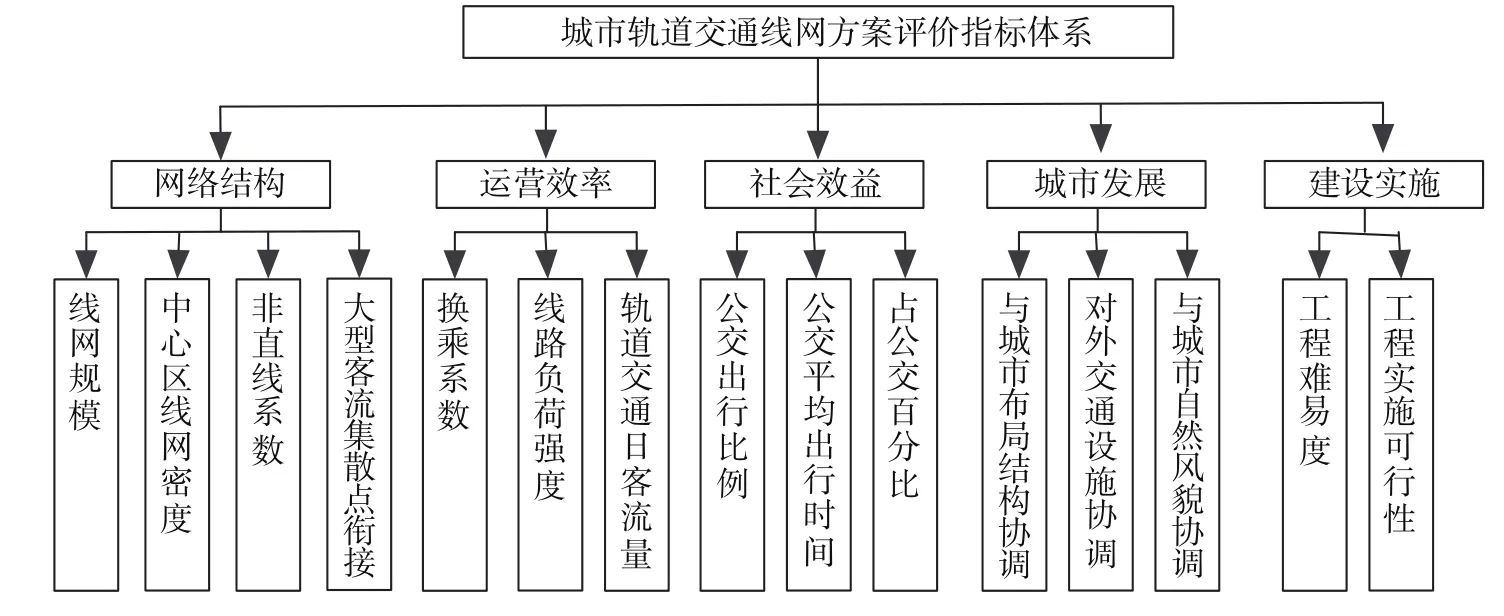
图3　轨道交通线网方案评价指标体系

图4　训练后的网络输出

图5　轨道交通线网方案 1

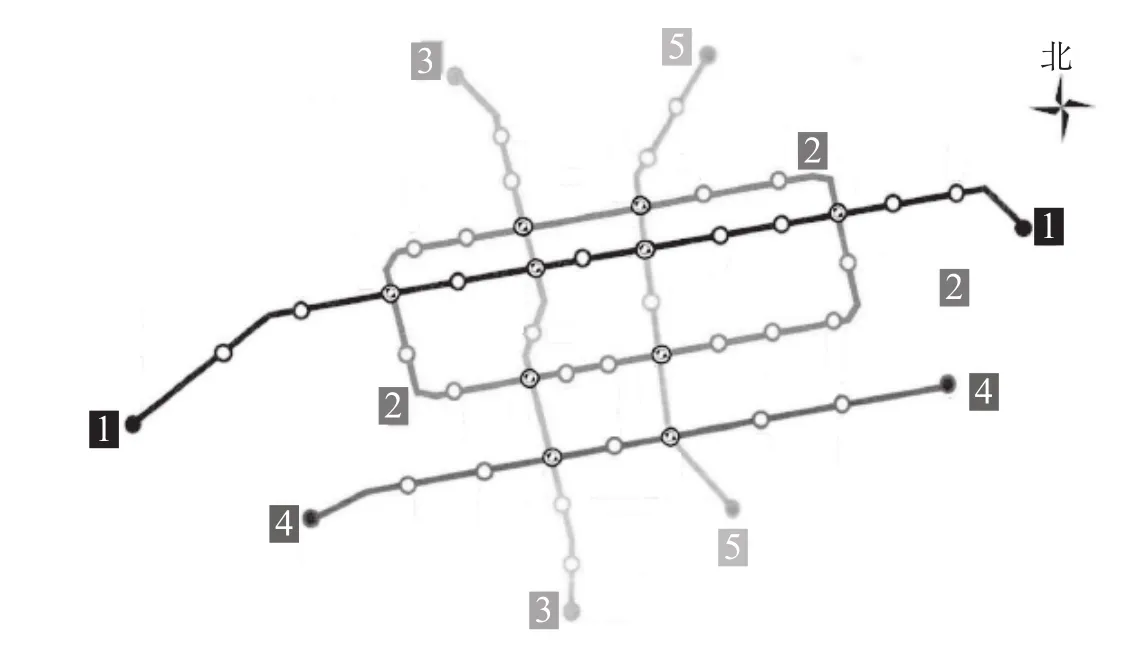
图6　轨道交通线网方案 2

方案 3：共 5 条线路，由U型线和放射线组成，线路总长度约 83 km，线路结构如图 7 所示。专家组对这 3 种规划方案的最终评分结果分别依次是0.81，0.88，0.84 (满分为 1 分)。

图7　轨道交通线网方案 3

组织专家组对指标体系中的 15 个指标进行评分，具体评分结果如表 4 所示。将表 4 所示的评分结果即为主成分模型中的参考样本值。

表4　城市轨道线网规划方案专家打分表

在对该市规划线网方案进行评定时，依据各指标评价综合值的打分情况，将各指标输入训练好的BP 神经网络，经过 5 次调整，具体评价结果如表 5所示。由表 5 可知，基于 PCA-BP 神经网络对该市轨道交通线网方案进行评价，所得结果与专家对照评价的结果吻合度较高，说明建立的模型具有一定的稳定性。评价结果中，第 2 套方案最佳，可以作为该市的交通线网布局方案。

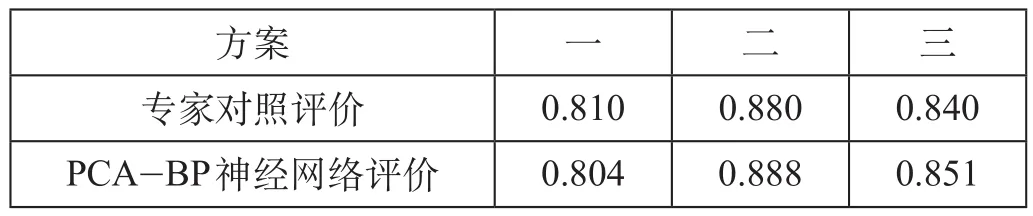
表5　线网方案评价综合值对比表

3　结束语

城市轨道交通线网方案评价是城市轨道交通线网布局规划的重要参考依据。基于 PCA-BP 神经网络的评价方法，考虑主成分分析法与 BP 神经网络的特点优势，并予以结合利用，既能够不遗漏城市轨道交通线网方案评价的重要指标，又能够保证各指标之间的相对独立，简化 BP 神经网络的输入，提高输出的评价精度。实例结果证明，提出的基于PCA-BP 神经网络的评价方法能够很好地适用于复杂的轨道交通线网方案评价，具有一定的理论意义和价值。同时，还应结合其他项目具体应用情况，进行验证及方法修正，进一步完善该评价方法。

[1] 李俊芳，吴晓萍. 基于多层次评判的城市轨道交通线网规划方案综合评价[J]. 武汉理工大学学报，2007，31(2)：205-208. LI Jun-fang，WU Xiao-ping. Synthetic Evaluation for Urban Rail Transit Line Network Planning Scheme based on AHP-Fuzzy Method[J]. Journal of Wuhan University of Technology，2007，31(2)：205-208.

[2] 王艳荣. 城市轨道交通线网规划方案评价方法及应用研究[D]. 北京：北京交通大学，2013. WANG Yan-rong. Research on Evaluation Method and Application for Urban Rail Transit Network Planning Program [D]. Beijing：Beijing Jiaotong University，2013.

[3] 赵长江. 城镇群城际轨道交通线网规划理论与应用研究[D]. 北京：中国铁道科学研究院，2009. ZHAO Chang-jiang. Study on Theory and Application of Intercity Rail Network Planning[D]. Beijing：China Academy of Railway Sciences，2009.

[4] 沈小燕，刘浩学，晏远春. 基于主成分分析和神经网络的综合安全评价模型[J]. 安全与环境学报，2009，9(1)：180-184. SHEN Xiao-yan，LIU Hao-xue，YAN Yuan-chun. A Renovated Safety Evaluation Model based on the Principal Component Analysis and BP Neural Network[J]. Journal of Safety and Environment，2009，9(1)：180-184.

[5] 张玉召，严余松，江 南，等. 基于 DEA 的城市轨道交通规划线网综合评价研究[J]. 铁道工程学报，2010，8(143)：97-99. ZHANG Yu-zhao，YAN Yu-song，JIANG Nan，et al. Evaluation of Urban Rail Transit Network Plan with DEA Method[J]. Jounal of Railway Engineering Society，2010，8(143)：97-99.

[6] 胡超凡. 北京城市轨道交通线网合理规模的研究[J]. 铁道运输与经济，2006，28(10)：52-54. HU Chao-fan. Research on Reasonable Scale of Urban Rail Network Transit in Beijing[J]. Railway Transport and Economy，2006，28(10)：52-54.

[7] 高国刚. 长春市城市快速轨道交通线网合理规模研究[D]. 长春：吉林大学，2014. GAO Guo-gang. Research of Reasonable Scale of Urban Rail Network Transit in Changchun City[D]. Changchun：Jilin University，2014.

[8] 金 键，张殿业，郭孜政. 城市轨道交通合理规模机理及模型分析[J]. 铁道学报，2006，5(3)：38-40. JIN Jian，ZHANG Dian-ye，Guo Zi-zheng. Demand Mechanism Model Analysis of Rational Scale of Urban Rail Transit Network[J]. Journal of the China Railway Society，2006，5(3)：38-40.

[9] 李俊辉，黎新华，谢小星. 基于概率神经网络的轨道交通车站客流安全状态评价[J]. 都市快轨交通，2015，28(4)：65-69. LI Jun-hui，LI Xin-hua，XIE Xiao-xing. Evaluation of Safety Status of Station Passengers in Urban Rail Transit based on Probabilistic Neural Network[J]. Urban Rapid Rail Transit， 2015，28(4)：65-69.

责任编辑：王 静

Study on Evaluation of Line-network Programs of Urban Rail Transit based on PCA-BP Neural Network

Through establishing the evaluation model of PCA-BP neural network, introducing the principal component analysis (PCA) and bP neural network algorithm into the evaluation process, based on making dimension reduction by using PCA at the same time of retaining initial information to maximum extent, the program of line-network layout is evaluated by exerting the advantages of BP neural network like solving nonlinear and complex problems. In the end, through actual example analysis, the evaluation method based on PCA-BP neural network is proved applicable for evaluation of line-network layout program and is an effective evaluation method of line-network program of urban rail transit.

Principal Component Analysis (PCA); bP Neural Network; Evaluation of Linenetwork Program

1003-1421(2016)02-0081-06

F213.2；N945.16

B

10.16668/j.cnki.issn.1003-1421.2016.02.17

2015-11-05

国家自然科学基金合作项目(61374157)；河北联合大学校基金项目(Z201409)