城市轨道交通行车组织优化控制模型研究

魏 博

WEI Bo

（中国铁道科学研究院 通信信号研究所，北京 100081）

(Signal & Communication Research Institute， China Academy of Railway Sciences， Beijing 100081， China)

城市轨道交通行车组织优化控制模型研究

魏 博

WEI Bo

（中国铁道科学研究院 通信信号研究所，北京 100081）

(Signal & Communication Research Institute， China Academy of Railway Sciences， Beijing 100081， China)

通过分析城市轨道交通行车组织的特点，根据对列车运行图兑现率的影响，将行车组织调整方式分为运行计划调整策略和径路变更调整策略 2 类。在考虑列车与列车之间和列车与车站之间的条件约束下，以恢复当日行车计划时的列车晚点总时间最小为优化目标，建立基于 2 类调整策略的行车组织优化控制模型，设计算法流程，利用广州地铁 7 号线的基础数据进行仿真实验，实验结果表明该模型具有可行性，能够为城市轨道交通行车组织提供辅助支持。

城市轨道交通；行车组织；调整策略；运行图兑现率；优化控制模型

城市轨道交通作为复杂而巨大的系统，具有内在的不稳定性[1]，因其乘客流量大、行车密度高、追踪间隔短等特点，有时一个小事件也可能造成列车晚点，导致晚点传播。在这种大范围晚点的情况下调整恢复至正常运转需要的时间较为漫长，影响城市轨道交通运输系统的效率，给行车组织工作带来巨大挑战。目前，关于行车组织优化控制的研究多集中于对列车运行计划调整建立数学模型及设计优化算法进行求解的领域，尤其铁路干线行车调度方面的研究工作已经取得一些成果[2-8]，以列车运行总晚点最少为基础建模，如Corman F等[2]建立列车运行调度的规划模型，孟令云等[3]提出两阶段带补偿随机期望值模型，并且设计了分枝定界方法求解等。为了研究和探索城市轨道交通列车运行调整问题，借鉴铁路行车调度的研究方法，提出突发事件下的城市轨道交通行车组织优化控制模型。

1　城市轨道交通行车组织的特点及调整策略分类

1.1特点

（1）调整时间冗余少。城市轨道交通客流密度大，行车密度高。在编制城市轨道交通计划运行图过程中，留给行车组织工作调整的冗余时间有限。

（2）实时性、复杂性要求高。城市轨道交通线路短，在线列车多，大多数情况下列车运行调整针对的不是 1 列或 2 列列车，而是一个列车群。因此，要求从全局出发，快速做出决策。

（3）约束条件多。城市轨道交通应满足列车与列车、列车与车站、计划列车时刻表等多方面约束条件，主要包括车站停站时间、车站折返能力、列车区间运行时间、列车追踪间隔等。

（4）优化指标多。减少实际运行图与计划运行图的偏差，即尽量保证运行图高兑现率；最小化所有列车的总延迟时间，即尽量提高列车正点率[9]，由于城市轨道交通行车组织方式不同于干线铁路，如果利用停运或中途停运等调整措施，在提高正点率的同时会降低运行图兑现率、减少旅客平均等待时间和列车区间运行速度等级的波动等。通过不同调整策略，在保证运行图高兑现率条件下使列车晚点总时间最小，消除晚点对后续列车计划的干扰。

1.2调整策略分类

行车调度员进行列车运行调整的方式包括调整停站时间、变更交路、实施跳停或扣车，如果晚点列车较多，则可以采用增加或减少上线列车等手段[10]。按照对各项指标和运行图兑现率的影响，将这些调整方式分为 2 类。一类为不影响运行图兑现率的计划调整策略，具体包括：①调整列车在始发站的出发时间；②调整列车的区间运行速度等级；③调整列车停站时间；④实施跳停；⑤实施扣车；⑥调整列车折返类型。另一类为影响运行图兑现率的径路变更调整策略，具体包括：①组织列车反方向运行；②增开或抽线[11]停运部分列车；③变更列车运行交路，组织列车在具备条件的中间站折返。

2　行车组织优化控制模型及算法

2.1优化控制模型

城市轨道交通在突发情况下的行车组织原则是采用最短时间尽可能地恢复按图行车，最终以列车的实际运行轨迹符合当时的列车运行计划为目的，以当日的运行计划收敛为目标。因此，将行车组织控制优化问题转化为一个扰动触发的闭环优化过程[12-13]。当突发事件产生扰动变更了当前的开行计划后，首先判定是否需要通过径路变更策略生成开行计划调整方案，如果需要则将输出结果反馈运行计划调整生成策略，如果不需要则直接进行运行计划调整策略生成，最终得出开行计划调整方案。如果方案的反馈结果不满意，则重新进行前述过程，直到得到满意解为止，然后输出结果。

2.2算法

2.2.1目标函数

控制模型的目标函数如下。

式中：∂ 为运行图兑现率，∂ = 线路实际开行列次/线路图定开行列次；Z 为列车晚点总时间最小，公式为

式中：I 为列车集合，I = {1，2，…，i，…，n}；S 为车站集合，S = {1，2，…，j，…，m}；di,j为列车 i在车站 j 的实际到达时间；Di,j为列车 i 在车站 j 的计划到达时间；fi,j为列车 i 在车站 j 的实际出发时间；Fi,j为列车 i 在车站 j 的计划出发时间。

由 ∂ 的定义可以看出，线路实际开行列数会直接影响列车晚点数量，进而影响列车晚点时间。因此，列车晚点总时间的计算在不同运行图兑现率情况下不相同。同时为了便于采用比例选择策略，将求最小化问题转换为求最大化问题，即对列车总晚点时间做加权变换，并以其作为适应度函数。

2.2.2约束条件

列车运行调整需要考虑约束条件，包括列车本身需要满足的约束、列车相互之间的约束，以及列车与车站之间的约束。

（1）列车停站时间约束。

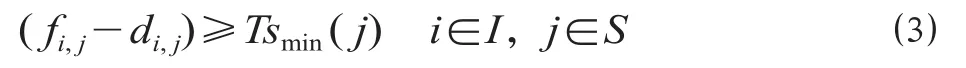
式中：Tsmin( j) 为 j 站最小停站时间。

（2）区间运行时间约束。

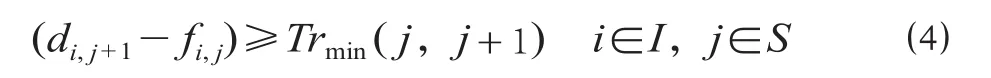
式中：Trmin( j，j + 1) 为相邻两站最小运行时间。

（3）列车追踪间隔约束。

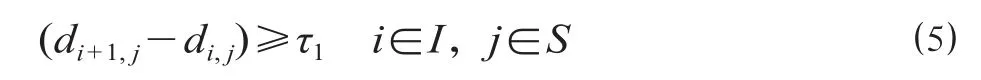
式中：τ1为列车最小追踪间隔时间。

（4）折返时间约束。

式中：τt( j) 为 j 站最小折返时间；Ig={1，2，…，p，…，k}为同服务号列车组；cj为 j 站折返标志，如果 j 站可以折返则取值为 1，否则为 0。

2.3模型求解

采用广度优化的方式调整列车运行计划，使其满足约束条件 ⑶、⑷、⑹，同时以最快速度收敛，形成开行计划调整方案的输出结果，尽量减少调整时间范围。广度优化根据各车组列车晚点评价水平调整列车运行线，通过调整列车的停站时间、区间运行速度等级和折返站的折返时间，检查该车组是否满足约束条件 ⑸，如果不满足，则需要增加车组列车恢复正点的时间，直至所有晚点列车恢复正点，然后进行径路变更策略调整。重复以上步骤，最终选择满足要求的开行方案作为输出结果。

2.4实证分析

以广州地铁 7 号线为例，采用其基础数据[13]，对上述模型算法进行模拟验证。该线路包含 9 个车站，分别是大学城南、南村、官堂、鹤庄、汉溪长隆、中村、谢村、石壁、广州南站，依次记为 S1，S2，…，S9。已知线路各项指标如下。最小停站时间为 20 s，列车之间的最小发车间隔采用 120 s，有 8 个运行区间，区间运行速度等级和区间运行时间均采用线路中的标准，S1 车站最小折返时间为 80 s，S9 车站最小折返时间为 120 s。

假设当日计划运行图各项指标如下。10 组列车对发，追踪间隔 202 s，开行交路为 S1—S9 交路，S1 和 S9 折返时间为 90 s、170 s，运转周期 2 050 s，首班列车始发时间为 7 : 13，末班列车终到时间为 20 : 56。故障发生时，上行列车 102 次、出发晚点 13 min 5 s，下行列车 091 次、出发晚点 13 min 50 s，后续列车依次晚点，列车运行图如图 1 所示。

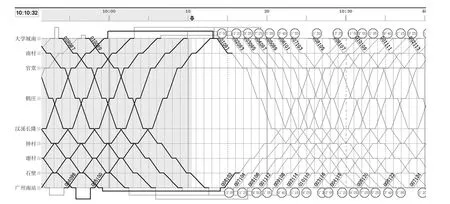
图1　故障发生时的列车运行图

分别进行 5 组实验：第 1 组，只按照计划调整策略进行调整，运行图兑现率为 100%；第 2 组至第 5 组，采用计划调整策略和径路变更调整策略共同调整，根据径路变更策略调整影响的线路实际开行列次不同，运行图兑现率分别为 99.578%、99.156%、98.734%、98.312%。5 组实验分别可以在末班列车入库到站前得到收敛结果，进一步得出运行图兑现率与正点率的关系如表 1 所示。

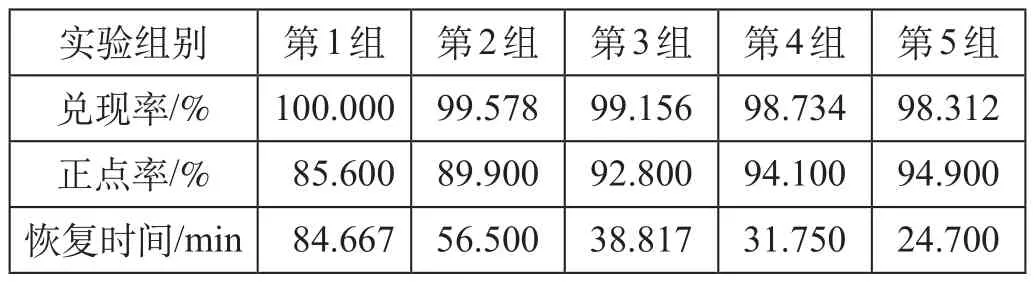
表1　各调整方案的运行图兑现率与正点率关系

由表 1 可以看出，第 1 组运行图兑现率最高，但正点率指标最低；而第 5 组运行图兑现率最低，其正点率则最高。由于这 5 组实验的结果在当日结束运营前均能恢复正点运行，表明 5 种调整方案均可行，行车组织调度人员可以根据实际运营需求选取合适的调整方案。例如，在满足正点率不低于 94% 的条件下，选取兑线率较高的方案 4 作为输出结果，优化调整方案 4 的结果如图 2 所示。由此可知，该模型能够根据某些调度运营实际需求，优化生成最优运营调整方案，表明该模型具有可行性。

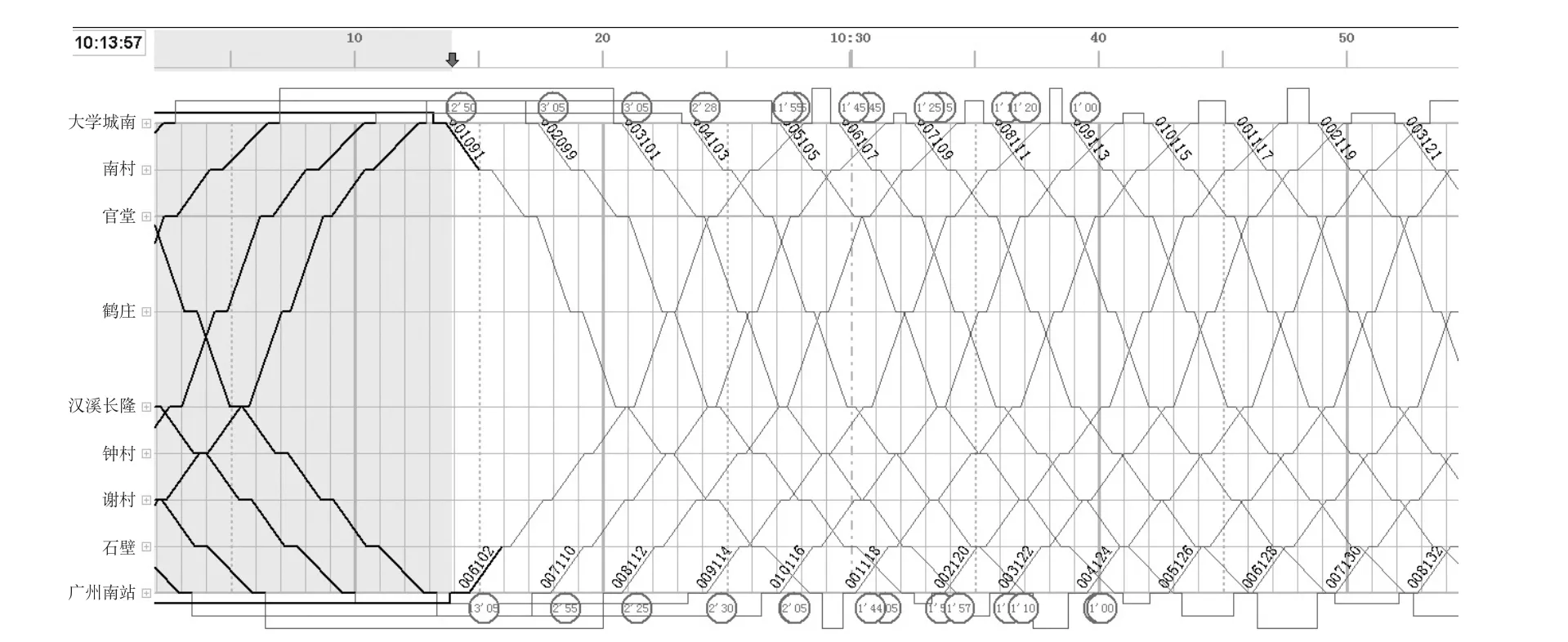
图2　优化调整方案的结果

3　结束语

研究运行图紊乱情况下行车组织优化控制问题不仅能丰富城市轨道交通运输组织理论，而且能进一步提升我国城市轨道交通运营效率。通过提出一种扰动情况下优化列车行车组织的模型，为现场列车运行组织工作提供决策支持，并且以广州 7 号线为例，验证该模型的有效性。然而，在保持运行图兑现率不变的条件下，不同径路变更策略调整方式对运行图调整性能的影响有待进一步地研究。

[1] Paquel C. Metro Traffic Regulation and Quality of Passenger Service：Performance Analysis of the Operational Control Center at RATP[D]. Delft：Delft University of Technology，2011.

[2] Corman F，D’Ariano A，Pacciarelli D, et al. Optimal Interarea Coordination of Train Rescheduling Decisions[J]. Transportation Research Part E (Logistics & Transportation Review)，2011，48(1)：71-88.

[3] 孟令云，杨肇夏，李海鹰. 单线铁路区间能力失效条件下列车运行调整模型[J]. 系统工程理论与实践，2012，32(4)：883-894. MENG Ling-yun，YANG Zhao-xia，LI Hai-ying. Train Dispatching Models under Field Capacity Breakdowns on Single-track Railway Lines[J]. Systems Engineering-Theory & Practice，2012，32(4)：883-894.

[4] 王宏刚，张 琦，王建英，等. 基于遗传算法的高速铁路行车调整模型[J]. 中国铁道科学，2006，27(3)：96-100. WANG Hong-gang，ZHANG Qi，WANG Jian-ying，et al. GA-based Model of Train Operation Adjustment for High-SpeedRailway[J]. China Railway Science，2006，27(3)：96-100.

[5] 刘皓伟. 行车指挥系统的 Petri 网建模与列车运行调整的遗传优化的研究[D]. 北京：中国铁道科学研究院，2000.

[6] 董守清，王进勇，闫海峰. 双线铁路列车运行调整的禁忌搜索算法[J]. 中国铁道科学，2005，26(4)：112-119. DONG Shou-qing，WANG Jin-yong，YAN Hai-feng. Tabu Search for Train Operation Adjustment on Double-track Line[J]. China Railway Science，2005，26(4)：112-119.

[7] 蒲 云，陈彦如，蒲 素. 基于遗传算法的列车运行调度指挥系统满意优化模型的求解[J]. 世界科技研究与发展，2001，23(6)：56-58. PU Yun，CHEN Yan-ru，PU Su. A Study on the Genetic Algorithm for Model of the Train Operation Dispatch Manage System based on Satisfactory Optimization[J]. World Sci-Tech R & D，2001，23(6)：56-58.

[8] 陈彦如，蒲 云，蒋阳升. 复线列车运行调整的满意优化模型体系及算法[J]. 科技通报，2002，18(6)：463-469. CHEN Yan-ru，PU Yun，JIANG Yang-shen. A Study on the Satisfactory Optimization Model and Solution for Adjusting Train Diagram on Double-Track Railway[J]. Bulletin of Science and Technology，2002，18(6)：463-469.

[9] 孙 涛. 提高旅客列车正点率措施的思考[J]. 铁道运输与经济，2014，36(2)：52-55. SUN Tao. Thoughts on Measures of Increasing Punctuality of Passenger Trains[J]. Railway Transport and Economy， 2014，36(2)：52-55.

[10] 刘浩江. 地铁行车组织中的调度调整方式[J]. 城市轨道交通研究，2008，11(1)：54-57. LIU Hao-jiang. Regulation Strategy for Train Organization[J]. Urban Mass Transit，2008，11(1)：54-57.

[11] 栾文波，王 栋. 基于客流变化的行车组织分析[J]. 都市快轨交通，2010，23(1)：71-73. LUAN Wen-bo，WANG Dong. Analysis of Train Organization based on Floating Passenger Flow[J]. Urban Rapid Rail Transit，2010，23(1)：71-73.

[12] 王 莉，朱 涛，徐 杰，等. 突发事件下旅客列车行车组织双层规划模型[J]. 东南大学学报 (自然科学版)，2015(5)：996-1001. WANG Li，ZHU Tao，XU Jie，et al. Bi-level Programming Model on Passenger Train Operation in Emergency[J]. Journal of Southeast University (Natural Science Edition)，2015(5)：996-1001.

[13] 王 莉. 突发实践条件下铁路行车组织模糊随机优化方法[D]. 北京：北京交通大学，2012.

责任编辑：冯姗姗

Study on Optimal Control Model of Train Operation Organization of Urban Rail Transit

Through analyzing characteristics of train operation organization of urban rail transit, according to the influence on fulfillment rate of train working diagram, the adjustment modes of train organization are divided into 2 categories including adjustment strategy of train operation scheme and adjustment strategy of route change. Considering condition restrictions between trains and between train and station, taking minimized total train delay time while resuming the sameday train operation scheme as optimization object, the optimal control model of train operation organization based on above 2 categories of adjustment strategies is established and its algorithm is designed, and then, the simulation is taken by using the basic data of Guangzhou Metro Line 7. The simulation result shows that the model is feasible and can provide auxiliary support for train operation organization of urban rail transit.

Urban Rail Transit; Train Operation Organization; Adjustment Strategy of Train Operation; Fulfillment Rate of Train Working Diagram; Optimal Control Model

1003-1421(2016)03-0079-05

U239.5；U293.1

A

10.16668/j.cnki.issn.1003-1421.2016.03.16

2016-02-01

2016-02-22

中国铁路总公司科技研究开发计划课题(2014X004-A)